Где используются уравнения высших степеней в жизни

Об уравнениях высших степеней

Как правило в физике, информатике и экономике мы сталкиваемся с простейшими линейными, или дробно-рациональными уравнениями, реже с квадратными. А что до уравнений третьей и четвёртой степени? Если вам интересно, то прошу под кат.

Для начала рассмотрим понятие уравнения высшей степени. Уравнением высшей степени, называется уравнение вида:

В этой статье я рассмотрю:

1. Кубические уравнения.
2. Возвратные кубические.
3. Применение схемы Горнера и теоремы Безу.
4. Возвратные биквадратные уравнения.

Кубические уравнения

Кубические уравнения, это уравнения, в которых у неизвестной при старшем члене степень равна 3. Кубические уравнения имеют следующий вид:

Решать такие уравнения можно по разному, однако мы воспользуемся знаниями базовой школы, и решим кубическое уравнение методом группировки:

В данном примере используется метод группировки, группируем первые два и последние два члена, получая равные скобки, снова выносим, получая уравнение из двух скобок.

Произведение равно нулю тогда, и только тогда, если хотя бы один из множителей равен нулю, на основании этого мы каждый множитель (скобку) приравниваем к нулю, получая неполное квадратное и линейное уравнения.

Также стоит отметить, что максимальное количество корней уравнения, равно степени неизвестной при главном члене, так в кубическом уравнении может быть не более трёх корней, в биквадратном (4-ой степени) не более четырёх корней и. т. д.

Возвратные кубические уравнения

Возвратные кубические уравнения имеют вид:

Возвратными они называются потому что коэффициенты будут зеркально повторяться. Подобные уравнения тоже решаются школьными методами, но чуть хитрее:

Сначала производится группировка, потом при помощи формул сокращённого умножения мы раскладываем получаемое на множители. Снова получаем 2 равные скобки, «выносим их». Получаем два множителя (скобки) и решаем их как два различных уравнения.

Теорема Безу и схема Горнера

Теорема Безу была открыта, как ни удивительно, Этьеном Безу, французским математиком, занимавшимся в основном алгеброй. Теорему Безу, можно сформулировать следующим образом:

Давайте разберёмся. P(x) — это какой-либо многочлен от x, (x — a) — это двучлен в котором a — это один из целых корней уравнения, который мы находим среди делителей свободного члена.

Три точки, это оператор обозначающий что одно выражение делится на другое. Из этого следует что найдя хотя бы один корень данного уравнения, мы сможем применить к нему эту теорему. Но зачем нужна эта теорема, каково её действие? Теорема Безу — это универсальный инструмент, если вы хотите понизить степень многочлена. Например, при её помощи, кубическое уравнение, можно превратить в квадратное, биквадратное, в кубическое и т. д.

Но одно дело понять, а как поделить? Можно конечно, делить и в столбик, однако этот метод доступен далеко не всем, да и вероятность ошибиться очень высока. Поэтому есть и иной путь, это схема Горнера. Её работу я поясню на примере. Предположим:

И так, нам дан многочлен, и мы возможно заранее нашли один из корней. Теперь мы рисуем небольшую табличку из 6 столбцов и 2 строк, в каждый столбец первой строки (кроме первого), мы вносим коэффициенты уравнения. А в первый столбец 2 строки мы вносим значение a (найденный корень). Потом первый коэффициент, в нашем случае 5, мы просто сносим вниз. Значения последующих столбиков мы рассчитываем так:

(Картинка позаимствована здесь)
Далее поступаем точно так же и с остальными столбцами. Значение последнего столбца (2 строки) будет остатком от деления, в нашем случае 0, если получается число отличное от 0, значит надо избрать другой подход. Пример для кубического уравнения:

Возвратные биквадратные уравнения

Выше мы так же рассматривали возвратные кубические уравнения, а теперь разберём биквадратные. Их общий вид:

В отличие от кубического возвратного уравнения, в биквадратном пары, относительно коэффициентов, есть не у всех, однако в остальном они очень схожи. Вот алгоритм решения таких уравнений:

Как видно, решать такие уравнения совсем не просто. Но я всё равно разберу и этот случай. Начинается решение с деления всего уравнения на x^2. Далее мы группируем, здесь я специально ввёл дополнительную строку для ясности. После этого мы совершаем хитрость, и вводим в первую скобку 2, которую мы сначала прибавляем, а после вычитаем, сумма всё равно не изменится, зато теперь мы можем свернуть эту скобку в квадрат суммы.

Уберём -2 из скобки, предварительно домножив его на a, после чего вводим новую переменную, t и получаем квадратное уравнение.

А теперь перейдём к примеру:

Основная часть так же как и в обобщённом алгоритме, делим на x^2, группируем, сворачиваем в полный квадрат, выполняем подстановку переменной и решаем квадратное уравнение. После этого полученные корни подставляем обратно, и решаем ещё 2 квадратных уравнения (с умножением на x).

Область применения

В виду своей громоздкости и специфичности уравнения высших степеней редко находят себе применение. Однако примеры всё же есть, уравнение Пуассона для адиабатических процессов в Физике.

Научно-исследовательская работа по теме: « Уравнения высших степеней»

Практика олимпиад, выпускных и вступительных экзаменов по математике показывает, что довольно часто приходится сталкиваться с уравнениями высших степеней. Решение таких уравнений зачастую вызывает большие трудности. Не все уравнения удается решить. В школьных учебниках уравнение высшей степени – редкость. В данной работе представлены методы решения указанных уравнений.

Цели работы: Узнать какие методы решения высших степеней существуют; Научиться решать уравнения высших степеней различными способами.

Задачи:

1.Подобрать необходимую литературу

2.Отобрать материал для исследования, выбрать главную, интересную, понятную информацию

3.Проанализировать и систематизировать полученную информацию

4.Найти различные методы и приёмы решения уравнений высших степеней

5.Классифицировать исследуемые уравнения

6.Оформить работу в виде буклета

7.Создать электронную презентацию работы для представления собранного материала

Объект исследования: уравнения высших степеней

Просмотр содержимого документа
«Научно-исследовательская работа по теме: « Уравнения высших степеней»»

Муниципальное казенное общеобразовательное учреждение

«Богучарская средняя общеобразовательная школа № 1»

по теме: « Уравнения высших степеней»

Автор: Жуковская Татьяна Владимировна , 9 «Б» класс

Руководитель: Алабина Галина Юрьевна

Великие учёные, изучавшие уравнения высших степеней….……. 6

Виды уравнений высших степеней………………………………………. ….9

Методы решения высших степеней……………….………………..…………9

Решение уравнений разными способами..………………….……………. 10

Решение уравнений высших степеней – история полная драматизма, разочарования и радости открытия. В течение почти 700 лет математики разных стран пытались найти приёмы решения уравнений третьей, четвёртой и более высоких степеней.

Только в 11 веке таджикский поэт и ученый Омар Хаям впервые решил уравнение III степени. Установить, существует ли формула для нахождения корней любого уравнения, пытались многие. В конце 18 века французский ученый Луи Лагранж пытался доказать невозможность алгоритма общих уравнений, а вначале 19 века француз Галуа развил идею Лагранжа.

С тех пор математика пошла другим путем. Ученые стали искать другие методы решения уравнений высших степеней.

Математическое образование, получаемое в общеобразовательной школе, является важнейшим компонентом общего образования и общей культуры современного человека. Практически все, что окружает современного человека – это все так или иначе связано с математикой. А последние достижения в физике, технике и информационных технологиях не оставляют никакого сомнения, что и в будущем положение вещей останется прежним. Поэтому решение многих практических задач сводится к решению различных видов уравнений, которые необходимо научиться решать.

Практика олимпиад, выпускных и вступительных экзаменов по математике показывает, что довольно часто приходится сталкиваться с уравнениями высших степеней. Решение таких уравнений зачастую вызывает большие трудности. Не все уравнения удается решить. В школьных учебниках уравнение высшей степени – редкость. Поэтому я выбрала эту тему для своей исследовательской работы.

1.Подобрать необходимую литературу

2.Отобрать материал для исследования, выбрать главную, интересную, понятную информацию

3.Проанализировать и систематизировать полученную информацию

4.Найти различные методы и приёмы решения уравнений высших степеней

5.Классифицировать исследуемые уравнения

6.Оформить работу в виде буклета

7.Создать электронную презентацию работы для представления собранного материала

Объект исследования: уравнения высших степеней

Методы исследования: изучение и анализ литературы, сравнение, обобщение, практический метод

Результат исследования: Я научилась решать возвратные и однородные уравнения,а также изучила теорему Безу и схему Горнера.

Гипотеза:Существует много различных видов и методов решения уравнений высших степеней, о которых не рассказывается в школьной программе 9 класса.

Великие учёные, изучавшие уравнения высших степеней

Омар Хайям (ок. 1048- ок. 1123)

Описал всевозможные виды уравнений третьей степени и рассмотрел сложные и красивые способы геометрических построений для отыскания их решения.

Никколо Тарталья (1499-1557)

Он вывел формулы для решения уравнений 3-ей степени, но своё открытие держал в тайне.

Обращался к Тарталье с просьбой сообщить ему формулу для решения кубических уравнений и обещал хранить её в секрете. Он не сдержал слово и опубликовал формулу, указав, что Тарталье принадлежит честь открытия «такого прекрасного и удивительного, превосходящего все таланты человеческого духа».

Нильс Хенрик Абель (1802-1829)

В 1826 году доказал, что нельзя вывести формулы для решения уравнений пятой степени и выше.

Этьен Безу (1730-1783)

Французский математик, член Парижской академии наук. Преподавал математику в Училище гардемаринов в 1763 и Королевском артиллерийском корпусе в 1768. Основные его работы относятся к алгебре (исследование систем алгебраических уравнений высших степеней, исключение неизвестных в таких системах и др.) Является автором шеститомного «Курса математики» (1764-1769).

Уильям Джордж Горнер (1786 – 1837)

Английский математик. Основные труды по теории алгебраических уравнений. С его именем связана (1819) схема Горнера деления многочлена на двучлен .

Виды уравнений высших степеней

Уравнения третьей степени

Уравнения четвёртой степени

Уравнения пятой степени

Способы решения уравнений высших степеней

Разложение многочлена на множители:

По формулам сокращенного умножения

По теореме Безу

Метод введения новой переменной

Данный способ применяют к многочленам, которые не имеют общего множителя для всех членов многочлена. Чтобы разложить многочлен на множители способом группировки, нужно: Объединить члены многочлена в такие группы, которые имеют общий множитель в виде многочлена. Вынести этот общий множитель за скобки.

Примеры решения уравнений способом группировки:

x-5=0 или x-4=0 или x+4=0

x-2=0 или x+2=0 или x-3=0

По формулам сокращенного умножения

1. Квадрат суммы: (a + b) 2 = a 2 + 2ab + b 2

2. Квадрат разности: (a — b) 2 = a 2 — 2ab + b 2

3. Разность квадратов: а 2 — b 2 = (a — b) (a + b)

4. Куб суммы: (a + b) 3 = a 3 + 3a 2 b + 3ab 2 + b 3

5. Куб разности: (a — b) 3 = a 3 — 3a 2 b + 3ab 2 — b 3

6. Сумма кубов: a 3 + b 3 = (a + b) (a 2 — ab + b 2 )

7. Разность кубов: a 3 — b 3 = (a — b) (a 2 + ab + b 2 )

Примеры решения уравнений с помощью формул сокращённого умножения:

x=1 D=16-64=-48-корней нет

+18a⁴+108a²+216=0

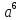
Исследовательская работа по математике «Уравнения высших степеней»

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

«Актуальность создания школьных служб примирения/медиации в образовательных организациях»

Свидетельство и скидка на обучение каждому участнику

Городской конкурс исследовательских работ «День науки»

Секция математики, информатики и физики

Способы решения уравнений высших степеней

Автор: Табакова Дарья Олеговна,

учащаяся 9 «Г» класса,

Средней общеобразовательной школы № 8

Пузырькова Вера Михайловна,

Средней общеобразовательной школы № 8

Аннотация

В курсе алгебры средней школы выводится формула для решения квадратного уравнения, а из курса физики видно, насколько необходима эта формула для решения многих физических вопросов (например, в задачах с равноускоренным движением).

Не меньшую роль, чем квадратные уравнения, играют в математике и её приложениях уравнения более высоких степеней. Люди почти так же давно начали заниматься уравнениями высших степеней, как и квадратными уравнениями.

В представленной научно-исследовательской работе рассмотрены различные методы решения уравнений высших степеней.

Введение

Актуальность: Данная тема актуальна, так как уравнения высших степеней встречаются в олимпиадных задачах, а также на Основном и Едином Государственном Экзамене. Однако эта тема недостаточно освещена в учебниках по алгебре в пределах общеобразовательной программы.

Цели и задачи проекта

Узнать, какие существуют методы решения уравнений высших степеней;

Научиться решать уравнения высших степеней различными способами.

Проанализировать источники литературы для выявления способов решения уравнений высших степеней;

Выделить логические приёмы решения уравнений высших степеней.

Омар Хайям (1048 – 1123)

В своих математических трудах таджикский ученый описал все возможные виды уравнений третьей степени и рассмотрел геометрический способ их решения.

Николо Тарталья (1499 – 1557)

Решил уравнение в радикалах.

Джероламо Кардано (1501 – 1576)

Обобщил приемы решения разных видов кубических уравнений. Независимо от Тартальи открыл формулу корней (формула Кардано).

Франсуа Виет (1540 – 1603)

Установил, каким образом корни уравнения выражаются через коэффициенты. Поставил вопрос о существовании решения уравнений произвольных степеней в радикалах.

Паоло Руффини (1765 – 1822)

Пытался доказать невозможность алгебраического решения общих уравнений выше четвертой степени.

Жозеф Луи Лагранж (1736 – 1813)

Искал признаки уравнений высших степеней, разрешимых в радикалах.

Нильс Хенрик Абель (1802 – 1829)

Доказал неразрешимость в радикалах уравнения пятой степени и более высоких степеней в общем случае.

Эварист Галуа (1811 – 1832)

Нашел необходимое и достаточное условие, которому удовлетворяет алгебраическое уравнение, разрешимое в радикалах.

Уильям Джордж Горнер (1786 – 1837)

Основные методы решения уравнений:

2.Применение формул сокращённого умножения. Выделение полного квадрата.

3.Метод разложения на множители. Вынесение общего множителя. Группировка.

4.Метод понижения степени. Теорема Безу.

5.Метод понижения степени. Схема Горнера.

6.Метод замены переменной.

7.Метод неопределённых коэффициентов.

8.Метод введения параметра.

1. Графический метод

Иногда полезно рассмотреть эскизы графиков функций y=f(x) и y=g(x), входящих в уравнение f(x)=g(x). Это может помочь выяснить:

1.На какие множества надо разбить числовую ось, чтобы на каждом из этих множеств использовать свой способ решения;

2.Наличие или отсутствие корней, их количество.

Пример №1: Решить уравнение х 6 +х 2 -8х+6=0.

Решение №1 : х 6 =-х 2 +8х-6.

Рассмотрим 2 функции: у=х 6 и у=-х 2 +8х-6.

Построим график функции у=х 6 .

Построим график функции у= -х 2 +8х-6. Это парабола, ветви которой направлены вниз. Хв=-8:(−2)=4; Ув=16+32-6=>т.В(4;10).

Судя по чертежу, построенные графики пересекаются в т.А(1;1). Проверка показывает, что на самом деле координаты т.А удовлетворяют обоим уравнениям. Значит, данное уравнение имеет один корень: х=1.

Пример №2 : Решить уравнение х 7 +3х+2=0.

Решение №2: х 7 =-3х-2.

Рассмотрим 2 функции у=х 7 и у=-3х-2.

Построим график функции у=х 7 .

Построим график линейной функции у=-3х-2. Это прямая, проходящая через т.т. (0;-2) и (1;-5).

По чертежу нельзя указать точный ответ, поэтому можно сказать только о приближенном значении решения уравнения х≈-0,6.

Графическое решение уравнения – наглядный способ, он хорош при необходимости определения наличия и отсутствия корней и их количества. Однако, графический метод не гарантирует того, что полученный результат является точным, поэтому найденные решения следует проверить.

2. Применение формул сокращённого умножения. Выделение полного квадрата

Этот метод основан на использовании формул:

𝑎 2 +2 𝑎𝑏 + 𝑏 2 = (a + b) 2

𝑎 2 −2 𝑎𝑏 + 𝑏 2 =( 𝑎 − 𝑏 ) 2

a 3 + b 3 = (a + b)(a 2 + ab + b 2 )

a 3 — b 3 = (a – b)(a 2 + ab + b 2 )

(a + b) 3 = a 3 + 3a 2 b + 3ab 2 + b 3

(a – b) 3 = a 3 – 3a 2 b + 3ab 2 – b 3

и метода группировки. Выделение полного квадрата – это такое тождественное преобразование, при котором заданный трёхчлен представляется в виде (а ± b) 2 .

Пример №3: х 4 –3х 2 +4х–3=0.

Решение №3: Представим -3х 2 =-2х 2 -х 2 и сгруппируем: (х 4 -2х 2 )-(х 2 -4х+3)=0

(х 4 -2х 2 +1-1)-(х 2 -4х+3+1-1)=0

(х 2 -1) 2 -1-(х-2) 2 +1=0

(х 2 -1-х+2)(х 2 -1+х-2)=0

Пример №4: х 4 =(3х-10) 2 .

(х 2 -3х+10)(х 2 +3х-10)=0

Алгоритм решения квадратных уравнений прост и понятен и используется практически во многих примерах и задачах. Однако, трудно об этом говорить, имея уравнения третьей, четвёртой и более высоких степеней. В тех из них, где можно привести к виду квадратного уравнения, следует тщательно потрудиться. Во многих случаях это приводит к нахождению решения уравнения.

3. Метод разложения на множители. Вынесение общего множителя. Группировка

Способ группировки можно разбить на 2 этапа:

Объединение членов многочлена в группы, имеющие общий множитель, и вынесение из каждой группы общего множителя.

Вынесение полученного общего для всех групп множителя за скобки.

Пример №5: 2х 8 -3х 7 +х 6 =0

Решение №5: х 6 (2х 2 -3х+1)=0

Пример №6: 2х 4 +3х 3 +16х+24=0.

Решение №6: (2х 4 +16х)+(3х 3 +24)=0

Способ разложения на множители очень эффективный, но при видимой простоте группировки очень непросто выбрать слагаемые для её проведения. Универсальных способов нет, так что приходится каждый раз экспериментировать.

4. Метод понижения степени. Теорема Безу

Формулировка теоремы Безу:

Остаток от деления многочлена Р(х) на двучлен (х – а) равен Р(а).

Следствия из теоремы Безу:

Число а – корень многочлена Р(х) тогда и только тогда, когда Р(х) делится без остатка на (х – а).

Свободный член многочлена делится на любой целый корень многочлена с целыми коэффициентами.

Если Р(а)=0, то заданный многочлен Р(х) можно представить в виде: Р(х)=(х-а)Q(x).

Пример №7: Решим уравнение х 3 +2х 2 -1=0.

Решение №7: Если это уравнение имеет целый корень, то он является делителем свободного члена, т.е. равен ±1. Проверка показывает, что х=-1. Значит, Р ₃ (х)=(х+1)Р ₂ (х), т.е. многочлен можно без остатка разделить на (х+1). х 3 +2х 2 -1=0

Пример №8: Решим уравнение х 4 +4х 3 -18х 2 -12х+9=0.

Решение №8: Если это уравнение имеет целый корень, то он равен одному из чисел: ±1;±3;±9. Проверка показывает, что х=-1. Значит, Р ₄ (х)=(х+1)Р ₃ (х), т.е. многочлен можно без остатка разделить на (х+1).

Разложим Р ₃ (х) на множители:

Этот способ решения уравнений – универсальный. Его можно применить для решения уравнений четвёртой, пятой и т.д. степеней, постепенно понижая их степени до второй.

5. Метод понижения степени. Схема Горнера

Схема Горнера (правило Горнера, метод Горнера) – алгоритм вычисления значения многочлена, записанного в виде суммы одночленов, при заданном значении переменной. Метод позволяет найти корни многочлена, также является простым алгоритмом для деления многочлена Р _n (x)=a ₀ x n +a ₁ x n-1 +a ₂ x n-2 +…+a _n-1 x+a _n на бином (х-а).

Пример №9 : Разделить 5х 4 +5х 3 +х 2 -11 на х-1, используя схему Горнера.

Решение №9: Составим таблицу из 2-х строк: в одной запишем коэффициенты по убыванию степеней х, во второй 1. Во вторую ячейку второй строки запишем 5, следующую заполним по такому принципу: 15+5=10. Далее 110+1=11, 111+0=11, 111-11=0.

Ответ: 5х 3 +10х 2 +11х+11.

Пример №10: найти все целочисленные корни многочлена х 6 +2х 5 -21х 4 -20х 3 +71х 2 +114х+45.

Решение №10: Коэффициенты многочлена – целые числа, а коэффициент перед старшей степенью переменной =1. Целочисленные корни нужно искать среди делителей свободного члена (±45;±15;±9;±3;±1). Итак, х=-1. Продолжим поиск корней. х 6 +2х 5 -21х 4 -20х 3 +71х 2 +114х+45=(х+1) 3 (х-3) 2 (х+5). Корни многочлена: -1;3;-5, причём -1 – корень третьего порядка, 3 – второго, -5 – корень первого порядка.

Конечно, данный метод подбора малоэффективен в общем случае, когда корни не являются целыми числами, но для целочисленных корней метод довольно-таки неплох. Схема Горнера даёт общий метод разложения на множители любого многочлена.

6. Метод замены переменной

В тех случаях, когда исходное уравнение может быть приведено к виду f(g(x))=0, заменой t=g(x) уравнение сводится к решению уравнения f(t)=0. Далее для каждого полученного корня tk решается уравнение g(x)=tk.

Пример №11: х 6 +3х 3 -4=0.

Решение №11 : Пусть t=x 3 , тогда t 2 +3t-4=0

Решение №12: (х 2 -3х)(х 2 -2х-х+2)=24

(х 2 -3х)(х 2 -3х+2)=24

Пусть t=х 2 -3х, тогда t(t+2)=24

х 2 -3х=-6 х 2 -3х=4

х 2 -3х+6=0 х 2 -3х-4=0

Основная проблема решения задач методом заключается в том, что иногда трудно угадать вид самой подстановки и вид уравнений, где подстановку можно использовать.

7. Метод неопределённых коэффициентов

Суть этого метода состоит в том, что заранее предполагается вид множителей, на которые разлагается данный многочлен. Этот метод опирается на следующие утверждения:

2 многочлена тождественно равны тогда и только тогда, когда равны их коэффициенты при одинаковых степенях х

Любой многочлен третьей степени разлагается в произведении линейного и квадратного множителей

Любой многочлен четвёртой степени разлагается в произведение 2х множителей второй степени.

Пример №13: 2х 4 -х 3 -9х 2 -х+1=0.

Решение №13 : 2х 4 -х 3 -9х 2 -х+1=(ах 2 +bx+c)(kx 2 +lx+n)=akx 4 +(al+bk)x 3 +(an+ck+bl)x 2 +(bn+cl)x+cn. a>0;k>0. ak=2, тогда пусть a=1,k=2; cn=1, отсюда с=1, n=1 или c=-1,n=-1.

ak=2 a=1,k=2 a=1,k=2

al+bk=-1 l+2b=-1 l+2b=-1

an+ck+bl=-9 1+2+bl=-9 -1-2+bl=-9

Вторая система не имеет решения, т.к. из второго и четвёртого уравнений получаем b=0,l=-1, что не удовлетворяет третьему уравнению. Получили: a=1,k=2,c=-1,n=-1,b=-2,l=3. Тогда разложение имеет вид: 2х 4 -х 3 -9х 2 -х+1=(х 2 -2х-1)(2х 2 +3х-1)

х 2 -2х-1=0 2х 2 +3х-1=0

Метод неопределённых коэффициентов является универсальным способом при разложении уравнения на простейшие, если нет рациональных корней.

8. Метод введения параметра

Метод введения параметра позволяет нестандартное уравнение привести к уравнению привычного вида (например, к квадратному уравнению).

Пример №14 : х 3 -(√3+1)х+3=0

Решение №14 : Пусть а=√3, то 3=а 2 .

а 2 -ах 2 +(х 3 -х 2 )=0

D=x 4 -4x 3 +4x 2 =x 2 (x 2 -4x+4)=x 2 (x-2) 2

Метод введения параметра используют в самых разных разделах алгебры. В частности, введением параметра могут быть решены некоторые тригонометрические, иррациональные и показательные уравнения.

Результаты исследования

Я проанализировала различные источники литературы, узнала, какие существуют методы решения уравнений высших степеней и научилась решать данные уравнения различными способами.

Каждый из приведённых мною способов заслуживает внимание. Какие-то уравнения можно решить несколькими способами, другие же – только одним. Но теорема Безу и схема Горнера – универсальные методы, применимые практически во всех уравнениях высших степеней.

Список использованных источников

1. А. Г. Курош «Алгебраические уравнения произвольных степеней» — М.: Просвещение, 1995.

2. И. Р. Шафаревич «Популярные лекции по математике. О решении уравнений высших степеней» Вып.15 — М.: Наука, 1954.

3. М. А. Еремин «Уравнения высших степеней» — Арзамас, 2003.

4. Л. М. Лоповок «1000 проблемных задач по математике» — М.: Просвещение, 1995.

источники:

http://multiurok.ru/files/nauchno-issliedovatiel-skaia-rabota-po-tiemie-urav.html

http://infourok.ru/issledovatelskaya-rabota-po-matematike-uravneniya-vysshih-stepenej-4570687.html