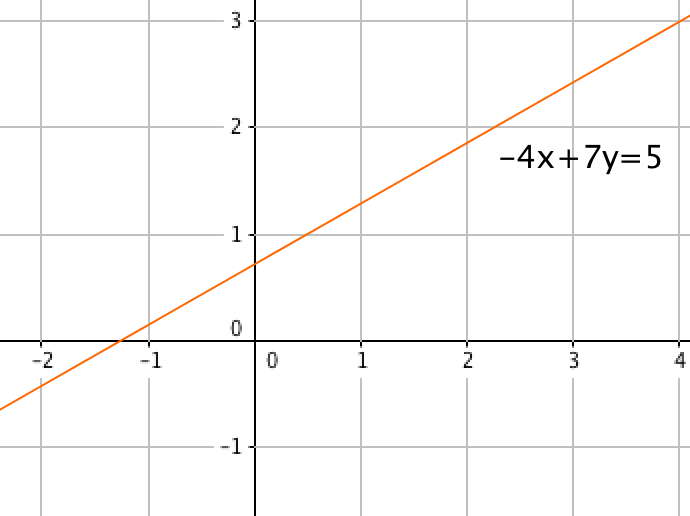Геометрическая точка зрения на систему линейных уравнений

15.4. Геометрическая интерпретация системы линейных уравнений

Как известно, уравнения с двумя переменными вида

Описывают на координатной плоскости Оху прямую. Система двух уравнений такого вида означает, что ее решения как точ­ки на координатной плоскости должны принадлежать одновре­менно двум прямым, соответствующим уравнениям этой сис­темы. Отсюда возможны следующие варианты: а) обе прямые пересекаются, и тогда система имеет единственное решение; б) прямые параллельны, и система не имеет решения (несов­местна); в) прямые совпадают, т. е. ранг системы равен едини­це, и система имеет бесчисленное множество решений.

Уравнение с тремя переменными вида

Описывает плоскость в трехмерном пространстве. Решение сис­темы трех уравнений с тремя неизвестными — это точки про­странства, принадлежащие одновременно трем плоскостям, ко­торые описываются уравнениями системы. В этом случае воз­можны следующие варианты: а) три плоскости пересекаются в одной точке, и система имеет единственное решение; б) три плоскости пересекаются по одной прямой — система имеет бесчисленное множество решений (все точки на этой прямой); в) две плоскости совпадают, а третья пересекает их — бес­численное множество решений (все точки прямой — на пересе­чении трех плоскостей), ранг системы равен двум; г) все три плоскости совпадают — все точки общей плоскости являются решениями, и ранг системы равен единице; д) хотя бы одна из плоскостей параллельна какой-либо из двух других — систе­ма несовместна; е) плоскости пересекаются попарно по парал­лельным прямым — система несовместна. В последних двух случаях несовместность системы уравнений обусловлена тем, что нет таких точек трехмерного пространства, которые принадлежали бы одновременно всем трем плоскостям.

В случае системы уравнений с N неизвестными каждое ура­внение вида

Можно интерпретировать как гиперплоскость в координатном пространстве An. Решение системы (15.1) — это множество точек пространства An, которые принадлежат одновременно всем M гиперплоскостям, соответствующим уравнениям этой системы.

Поверните устройство

1. Классы
2. 7 класс
3. 10. Системы линейных уравнений
4. Теория: 03. Геометрия решений системы линейных уравнений

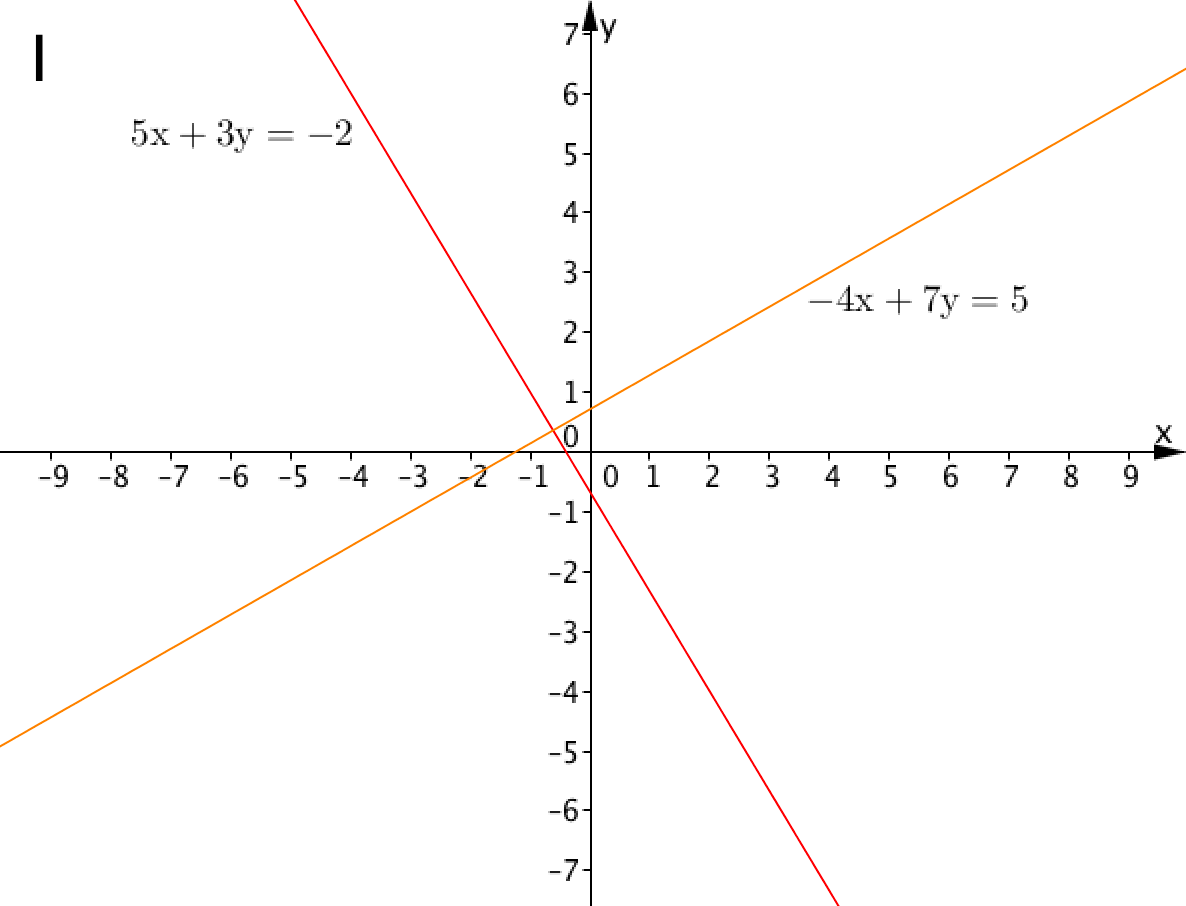
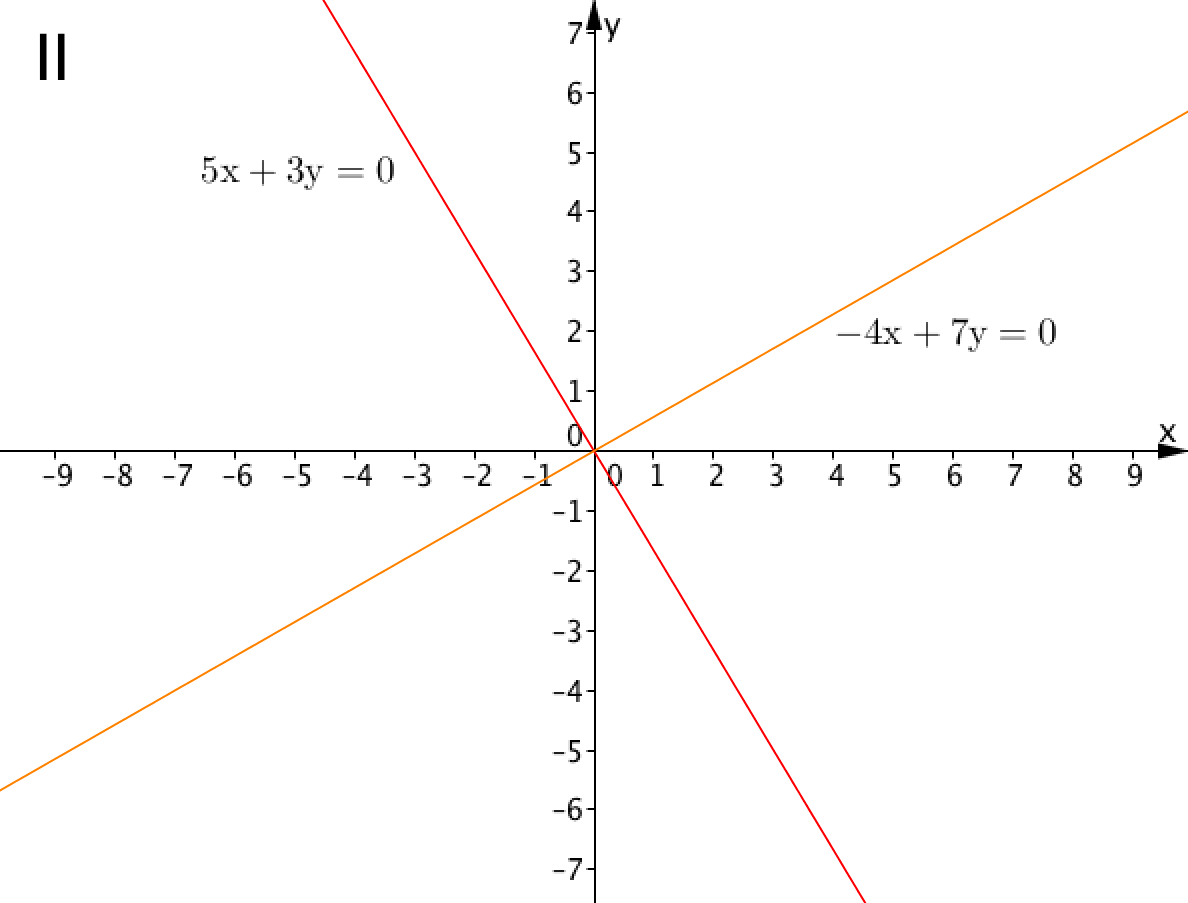
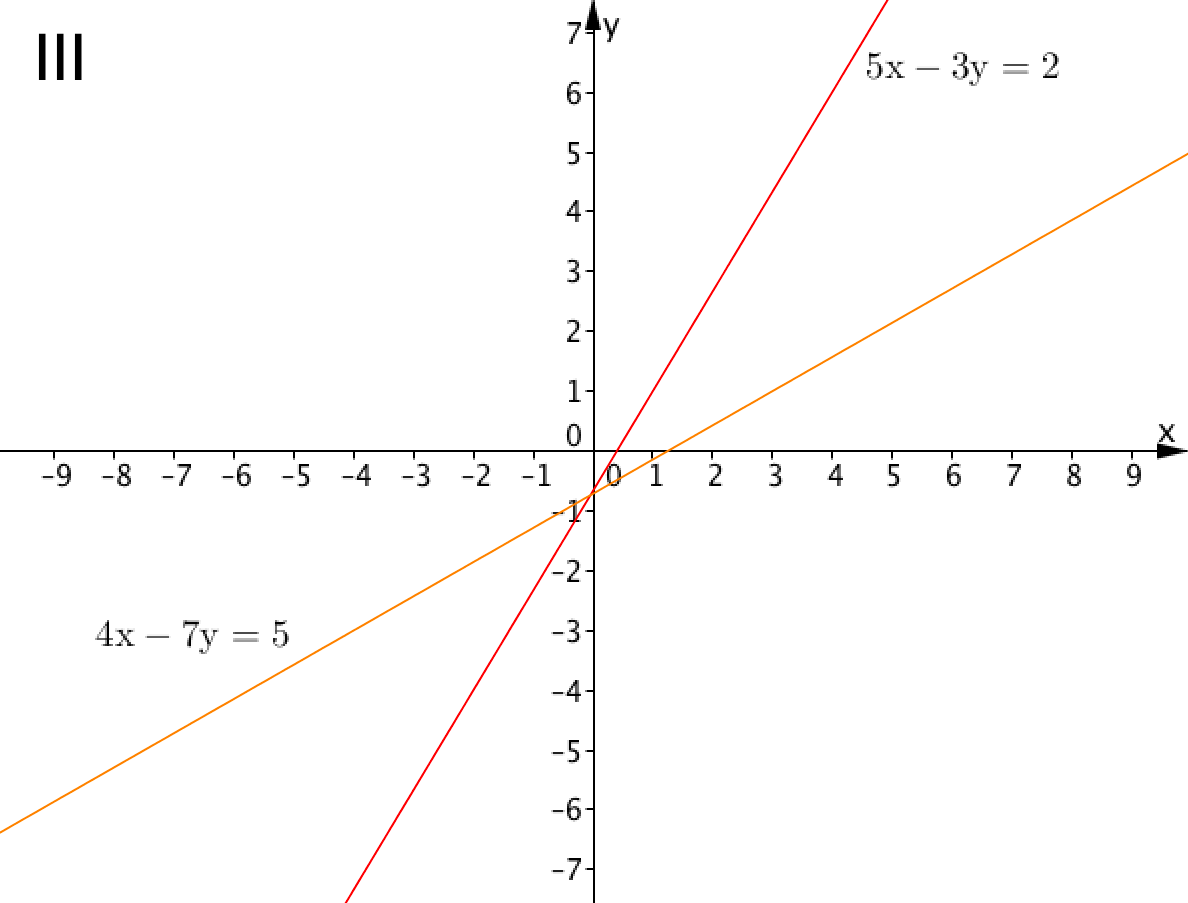
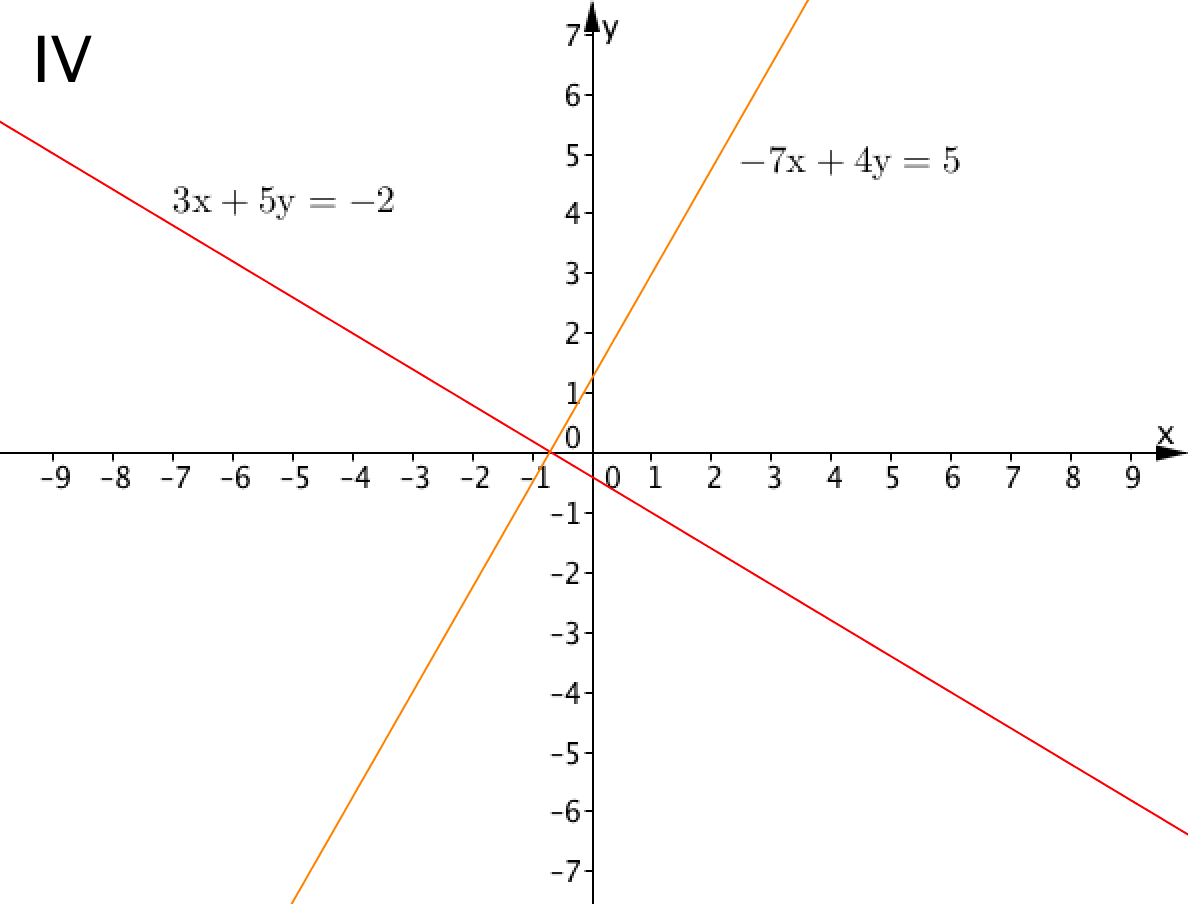
Выберите пару прямых, точка пересечения которых соответствует решению системы линейных уравнений:

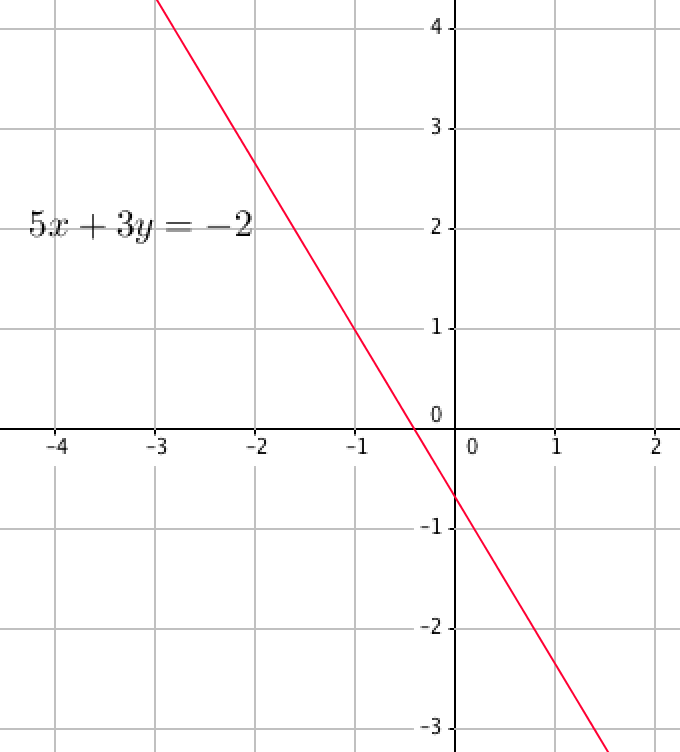
С геометрической точки зрения, решением системы уравнений

является точка с координатами \(\displaystyle (x_0;\, y_0)<\small ,>\) которая одновременно лежит на прямой \(\displaystyle 5x+3y=-2\)

и прямой \(\displaystyle -4x+7y=5\)

Этой точкой является точка пересечения прямых \(\displaystyle 5x+3y=-2\) и \(\displaystyle -4x+7y=5<\small .>\)

Таким образом, правильным ответом является вариант \(\displaystyle <\rm I><\small .>\)

Геометрическое истолкование линейной системы двух уравнений. Неопределенная и противоречивая системы

I

— у системы 1 решение.

II

пусть х₀у₀ — какое-нибудь решение 2-го уравнения, подставляем:

решение второго уравнеиня не удовлетворяет первое.

Противоречивая система — не имеет решений.

второе уравнение равно первому умноженному на какое-либо число или второе уравнение является следствием первого.

Неопределенной системойназывается система, имеющая бесконечное количество значений.

Геометрическое истолкование линейной системы трех уравнений. Неопределенная и противоречивая системы.

В пространстве Oxyz каждому из уравнений соответствует плоскость. Рассмотрим все возможные случаи взаимного расположения этих плоскостей.

1. Основной определитель Д¹0. По правилу Крамера находится единственное решение системы. Геометрически — это координаты единственной точки пересечения всех трех плоскостей.

2. Д=0 Много возможностей.

А) все три плоскости совпадают.

х+2у+z=2 2-ое и 3-е мы полу-

3х+6у+3z =6 чаем из 1-го, умно-

2х+4у+2z=4 жая их на 3 и 2 соответственно.ÞСистема неопределена. Отбрасываем 2 и 3 ур. и из оставшегося вычисляем z=2-х-2у. Давая различные значения х и у, вычислим соответствующее значение z и получим решение системы Таких решений бесконечное множество.

Б) Две плоскости совпадают, а 3-я их пересевает по одной прямой (т.е. не сливается с ними)Þможно отбросить одно уравнение, оставив уравнения любых двух несливающихся плоскостей. Эта система явл. неопред: значение одной из неизвестных задается произвольно, две другие вычисляются из упомянутой системы. Аналогичный результат получается, когда 3 плоскоти пересекаются по одной прямой, попарно не совпадая.

Если 1 и 3 сложить, то получится 2. И наоборот, если из 3-1, то получим 2.

В) 2 или 3 плоскости ||

При этом когда 2 || , третья либо их пересекает, либо совпадает с одной из нихÞ система противоречива.

Г) плоскости попарно пересекаются. Линии пересечения || между собой (их 3)Þ система противоречива.

*** Если в однородной системе все миноры 2-го порядка =0, решение зависит от 2х параметров., или хотябы один отличен от нуля, то решение зависит от одного пораметра.

Сложение векторов, умножение вектора на скаляр. Проекция вектора на ось. Коллиниарность и комплиментарность векторов.

Вектором называется величина, которая характеризуется не только численным значением, но и направлением в пространстве. Модулем |ā| или длиной вектора а наз его числ. зн-ие. Если |ā|=0, вектор называют нулевым..

Проекция вектора на ось.

Пусть в пространстве даны вектор ĀВ и ось Ох. Опустим ^ на ось Ох и з точек А и В, т.е. спроектируем эти точки на ось Ох. Обозначим проекции через А’ и В’ Вектор A’B’ называют компонентой вектора АВ по оси Ох. Проекцией вектора АВ на ось Ох называется длинна компоненты, взятая со знаком «+», если направление оси и компоненты совпадают, и со знаком «-» если направления противоположны.