Геометрический способ отбора корней в тригонометрических уравнениях

5 способов отбора корней в тригонометрических уравнениях

Исследовательская работа для подготовки к ЕГЭ (13 задание профильной математики)

Скачать:

Предварительный просмотр:

Межрегиональная научно-практическая конференция

посвященная Году экологии в Российской Федерации.

Тема: «5 способов отбора корней в тригонометрических уравнениях»

Физико-математический (физика, математика, информатика)

Кудряшова Светлана Олеговна,

ученица 10 класса МБОУ «Азбабинская СОШ»

Апастовского муниципального района РТ

Способы отбора корней в тригонометрических уравнениях………………..3 стр.

Алгебраический способ……………………………………………………… ..4 стр

Геометрический способ: изображение корней на тригонометрической

Геометрический способ: изображение корней на числовой прямой……….5 стр.

Функционально-графический способ…………………………………………6 стр

Список использованной литературы………………………………………….8 стр.

Уравнения и системы уравнений занимают важное место в математике. В 10 классе очень много внимания уделяется решению тригонометрических уравнений. Для успешного решения тригонометрических уравнений необходимо знать не только формулы и методы решения этих уравнений, но и правильно отбирать корни на заданном промежутке или при других дополнительных условиях. Следует также отметить, что в профильном варианте ЕГЭ по математике в 2017 году 13 задание это- «Решить тригонометрическое уравнение и выполнить отбор корней, удовлетворяющих условию или решить систему уравнений». Поэтому в данной работе я решила исследовать различные способы отбора корней в тригонометрических уравнениях, что поможет в дальнейшем для успешной сдачи ЕГЭ по математике.

Объект исследования: тригонометрические уравнения.

Предмет исследования: способы отбора корней в тригонометрических уравнениях.

Цель работы: Изучить различные способы отбора корней в тригонометрических уравнениях.

• определить наиболее рациональный способ отбора корней для каждого типа заданий;
• рассмотреть примеры решения уравнений, где необходимо выполнить отбор корней;

1) Изучение литературы

2)Анализ и обобщение изученной информации

3) Решение тригонометрических уравнений

Теоретическая значимость исследования заключается в том, что помимо распространённого способа отбора корней с помощью тригонометрической окружности, в меньшей мере используются арифметический и алгебраический подходы. Ученик, знающий несколько приёмов отбора корней, может при решении уравнения выбрать более рациональный.

Прикладная значимость результатов исследования определяется вкладом в развитие логического математического мышления, развитие умения самостоятельного решать тригонометрические уравнения различными способами. Результаты исследования могут быть использованы на уроках математики, а также при подготовке к ЕГЭ по математике.

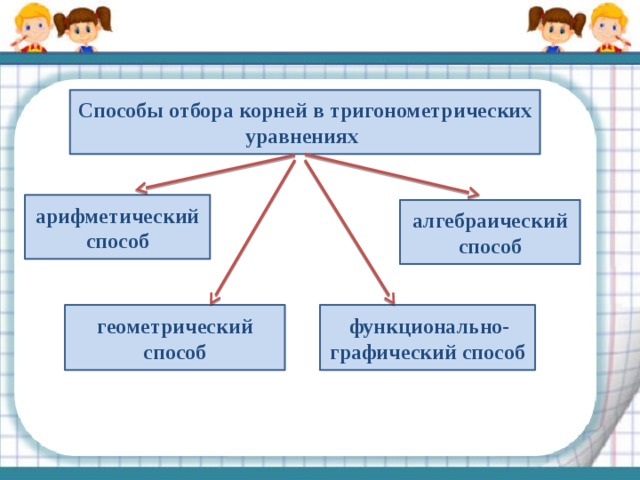
Способы отбора корней в тригонометрических уравнениях

При отборе корней в процессе решения тригонометрических уравнений обычно используют один из следующих способов.

• Арифметический способ: перебор значений целочисленного параметра и вычисление корней.
• Алгебраический способ: решение неравенства относительно неизвестного целочисленного параметра и вычисление корней.
• Геометрический способ:

— изображение корней на тригонометрической окружности с последующим отбором с учетом имеющихся ограничений;

— изображение корней на числовой прямой с последующим отбором с учетом

Каждый из этих способов по-своему хорош и удобен для применения в том или ином случае.

Сначала решим уравнение в общем виде :

а) 1- 2 x +3 x =1, 25

б)А теперь надо найти решения данного уравнения на промежутке [ 𝝅 ; 5 𝝅/2 ]

I. Арифметический способ: перебор значений целочисленного параметра и вычисление корней.

Придадим параметру k последовательно значения 0, 1.2, …, -1.-2, … и подставим эти значения в общую формулу.

Если k=0, то х=± 𝝅/6 не входит в промежуток [ 𝝅 ; 5 𝝅/2 ]

Если k=1, то х= 𝝅/6 + 𝝅 =7 𝝅 /6 это число входит в данный промежуток

х=- 𝝅 /6 + 𝝅 =5 𝝅/6 это число не входит в данный промежуток

Если k=2, то х= 𝝅/6 + 2𝝅 =13 𝝅 /6 это число входит в данный промежуток

х= -𝝅/6 + 2𝝅 =11 𝝅 /6 это число входит в данный промежуток.

Итак, заданному отрезку принадлежат те корни уравнения, которые получаются из общей формулы при следующих значениях параметра: k=1, 2. Эти корни таковы: 7 𝝅 /6 ; 11 𝝅/6 ;13 𝝅/6 .

II. Алгебраический способ: решение неравенства относительно неизвестного целочисленного параметра и вычисление корней.

Так как должно выполняться условие 𝝅≤х≤ 5 𝝅/2, то для первой серии имеем

𝝅≤ 𝝅 /6+ 𝝅 k ≤ 5 𝝅/2 ⇔ 1 ≤ 1 /6+k ≤ 5/2 ⇔ 1-1 /6 ≤ k ≤ 5/2- 1/6 ⇔ 5/6 ≤ k ≤ 7/3, то k= 1; 2.

Тогда х=7 𝝅 /6 ; х=13 𝝅 /6

Для второй серии имеем 𝝅≤ -𝝅 /6+ 𝝅 k ≤ 5 𝝅/2 ⇔ 1 ≤ -1 /6+k ≤ 5/2 ⇔

1+ 1 /6 ≤ k ≤ 5/2+ 1/6 ⇔ 7/6 ≤ k ≤1 7/6, то k= 2.

Итак, 7 𝝅/6 ; 11 𝝅/6 ;13 𝝅/6

III. Геометрический способ:

Изображение корней на тригонометрической окружности с последующим отбором с учетом имеющихся ограничений;

Все числа вида α+2 𝝅k, где k𝟄Z, соответствуют единственной точке числовой окружности, так как при обходе окружности в положительном или отрицательном направлении на целое число оборотов из данной точки мы приходим в эту же точку.

Проведем отбор корней, используя тригонометрическую окружность. Во-первых , на тригонометрической окружности отметим промежуток [ 𝝅 ; 5 𝝅/2 ] , длина которого 3π /2. Для этого полученные значения в серии решений изобразим на тригонометрической окружности . Из рисунка видно, что в интересующий нас промежуток входят только три значения из этих серий:

IV. Геометрический способ: изображение корней на числовой прямой с последующим отбором с учетом имеющихся ограничений.

Тригонометрическую окружность удобно использовать для изображения точек вида α+βn, n 𝟄Z, где отношение 2π:β- натуральное число. Ещё одна причина выбора числовой прямой связана с периодами функций, превосходящих 2π.

Итак, на числовой прямой рассмотрим промежуток [ 𝝅 ; 5 𝝅/2 ] . У нас 2 серии ответов: x= — 𝝅 /6+ 𝝅 k и x= 𝝅 /6+ 𝝅 k

Отметим точками числа:- — 𝝅 /6; 𝝅 /6; 𝝅 ; 5 𝝅/2; 7𝝅/6, 11𝝅/6; 13 𝝅/6.

На рисунке видно, что числа 7𝝅/6, 11𝝅/6; 13 𝝅/6 входят в промежуток [ 𝝅 ; 5 𝝅/2 ] .

Ответ: 7𝝅/6, 11𝝅/6; 13 𝝅/6

V. Функционально-графический способ

При решении тригонометрических уравнений иногда используются графики тригонометрических функций. При этом подходе требуется умение схематичного построения графика тригонометрической функции и применение формул корней соответствующих уравнений. Схематично изобразим графики функций y=sinх и y=0,5 , y= -0,5. Найдем три корня уравнения на промежутке [ 𝝅 ; 5 𝝅/2 ] . Это 7𝝅/6, 11𝝅/6; 13 𝝅/6

В своей работе я рассмотрела 5 способов отбора корней при решении тригонометрических уравнений с выбором ответа.

Проведя анализ всех решений, я пришла к выводу, что иногда уместно отобрать корни разными способами, чтобы твёрдо знать, что отбор выполнен верно.

Таким образом, арифметический способ самый простой, но он становится не эффективным в следующих случаях:

-заданные ограничения охватывают большой промежуток, и последовательный перебор значений приводит к громоздким вычислениям;

-серии решений содержат нетабличные значения обратных тригонометрических функций;

-требуется определить количество корней уравнения, удовлетворяющих дополнительным условиям.

Во всех случаях, перечисленных выше, удобен алгебраический способ отбора корней. Тригонометрическую окружность удобно использовать при отборе корней на промежутке, длина которого не превосходит 2π, или в случае, когда значения обратных тригонометрических функций, входящих в серию решений, не являются табличными.

Работа нашла своё применение и на уроках математики, а так же при подготовке к ЕГЭ по математике.

Способы отбора корней в тригонометрических уравнениях

Класс: 10

Автор проекта:
Шелкова Полина,
Класс: 10

Руководитель:
Злобова Людмила Викторовна,
учитель математики

ВВЕДЕНИЕ

Слово «тригонометрия» греческое, оно переводится как «измерение треугольников» (τρίγονον — «тригон» — треугольник и μετρειν — «метрео» — измеряю).

Тригонометрия, как и всякая другая наука, выросла из практической деятельности человека. Потребности развивающегося мореплавания, для которого требовалось умение правильно определять курс корабля в открытом море по положению небесных светил, оказали большое влияние на развитие астрономии и тесно связанной с ней тригонометрией. Предполагают, что основополагающее значение для развития тригонометрии в эпоху ее зарождения, имели работы древнегреческого астронома Гиппарха Никейского (180-125 лет до н. э.) (прил. №3). Систематическое использование полной окружности в 360° установилось в основном благодаря Гиппарху и его таблице хорд (прил. №2). Т.е. таблицы, которые выражают длину хорды для различных центральных углов в круге постоянного радиуса, что является аналогом современных таблиц тригонометрических функций. Впрочем, до нас не дошли оригинальные таблицы Гиппарха, как и почти все, что им написано. И мы, можем составить себе о них представление главным образом по сочинению «Великое построение» или «Альмагесту» знаменитого астронома Клавдия Птолемея, жившего в середине II века н.э.

Несмотря на то, что в работах ученых древности нет «тригонометрии» в строгом смысле этого слова, но по существу они, пользуясь известными им средствами элементарной геометрии, решали те задачи, которыми занимается тригонометрия. Например, задачи на решение треугольников (определение всех сторон и углов треугольника по трем его известным элементам), теоремы Евклида и Архимеда представленные в геометрическом виде, эквивалентны специфическим тригонометрическим формулам. Главным достижением средневековой Индии стала замена хорд синусами. Это позволило вводить различные функции, связанные со сторонами и углами прямоугольного треугольника. Таким образом, в Индии было положено начало тригонометрии, как учению о тригонометрических величинах.

Учёные стран Ближнего и Среднего Востока с VIII века развили тригонометрию своих предшественников. Уже в середине IX века среднеазиатский учёный аль-Хорезми написал сочинение «Об индийском счёте». После того, как трактаты мусульманских ученых были переведены на латынь, многие идеи греческих, индийских и мусульманских математиков стали достоянием европейской, а затем и мировой науки. В дальнейшем потребности географии, геодезии, военного дела, способствовали развитию тригонометрии. Особенно усиленно шло ее развитие в средневековое время. Большая заслуга в формировании тригонометрии как отдельной науки принадлежит азербайджанскому ученому Насир ад-Дину ат-Туси (1201-1274), написавшему «Трактат о полном четырехстороннике». Творения ученых этого периода привели к выделению тригонометрии как нового самостоятельного раздела науки. Однако в их трудах еще не была введена необходимая символика. Современный вид тригонометрия получила в трудах Леонарда Эйлера (1707-1783). На основании трудов Эйлера были составлены учебники тригонометрии, излагавшие ее в строгой научной последовательности (прил. №4). Тригонометрические вычисления применяются во многих областях человеческой деятельности: в геометрии, в физике, в астрономии, в архитектуре, в геодезии, инженерном деле, в акустике, в электронике и т.д.

I РАЗДЕЛ (теоретический)

Тема проекта и её актуальность: почему я выбрала тему «Способы отбора корней в тригонометрических уравнениях»?

• Расширить и углубить свои знания, полученные в курсе геометрии 8-9 класса.
• Тригонометрические уравнения рассматриваются в курсе алгебры и начал математического анализа 10-11 класса.
• Тригонометрические уравнения включены в КИМы ЕГЭ по математике.

Решение тригонометрических уравнений и отбор корней, принадлежащих заданному промежутку — это одна из сложнейших тем математики, которая выносится на Единый Государственный Экзамен. По результатам анкетирования многие учащиеся затрудняются или вообще не умеют решать тригонометрические уравнения и особенно затрудняются в отборе корней, принадлежащих промежутку. Немаловажно также знать, тригонометрические формулы, табличные значения тригонометрических функций для решения целого ряда заданий Единого Государственного Экзамена по математике.

Цель проекта: изучить способы отбора корней в тригонометрических уравнениях и выбрать для себя наиболее рациональные подходы для качественной подготовки к ЕГЭ.

Задачи:

• познакомиться с историческими сведениями о возникновении тригонометрии, как науки;
• изучить соответствующую литературу;
• научиться решать тригонометрические уравнения;
• найти теоретический материал и изучить методы отбора корней в тригонометрических уравнениях;
• научиться отбирать корни в тригонометрических уравнениях, принадлежащим заданному промежутку;
• подготовиться к ЕГЭ по математике.

Приёмы отбора корней тригонометрического уравнения на заданном промежутке.

При решении тригонометрических уравнений предлагается провести отбор корней из множества значений неизвестного. В тригонометрическом уравнении отбор корней можно осуществлять следующими способами: арифметическим, алгебраическим, геометрическим и функционально-графическим.

Арифметический способ отбора корней состоит в непосредственной подстановке полученных корней в уравнение, учитывая имеющиеся ограничения, при переборе значений целочисленного параметра.

Алгебраический способ предполагает составление неравенств, соответствующих дополнительным условиям, и их решение относительно целочисленного параметра.

Геометрический способ предполагает использование при отборе корней двух вариантов: тригонометрической окружности или числовой прямой. Тригонометрическая окружность более удобна, когда речь идет об отборе корней на промежутке или в случае, когда значение обратных тригонометрических функций, входящих в решения, не являются табличными. В остальных случаях предпочтительнее модель числовой прямой. Числовую прямую удобно использовать при отборе корней на промежутке, длина которого не превосходит 2 или требуется найти наибольший отрицательный или наименьший положительный корень уравнения.

Функционально-графический способ предполагает отбор корней осуществлять с использование графиков тригонометрических функций. Чтобы использовать данный способ отбора корней, требуется умение схематичного построения графиков тригонометрических функций.

II РАЗДЕЛ (практический)

Покажу практически три наиболее эффективных и рациональных, с моей точки зрения, метода отбора корней на примере решения следующего тригонометрического уравнения:

sinx−cos2x=0; [применили формулу двойного угла: cos2x = cos 2 x−sin 2 x]

sinx−(cos 2 x−sin 2 x)=0;

sinx−(1−sin 2 x−sin 2 x)=0;

Введем новую переменную: sinx = t, -1 ≤ t ≤1, получим

Вернемся к замене:

б) Рассмотрим три способа отбора корней, попадающих в отрезок .

1 способ: обратимся к единичной окружности. Отметим на ней дугу, соответствующую указанному отрезку, т.е. выполним отбор корней арифметическим способом и с помощью тригонометрической окружности:

2 способ: указанный отрезок соответствует неравенству: Подставим в него полученные корни:

3 способ: разместим корни уравнения на числовой прямой. Сначала отметим корни, подставив вместо n, и нуль (0), а потом добавим к каждому корню периоды.

Нам останется только выбрать корни, которые попали в нужный нам отрезок.

ЗАКЛЮЧЕНИЕ

При работе над моим проектом я изучила методы решения тригонометрических уравнений и способы отбора корней тригонометрических уравнений. Выяснила для себя положительные и отрицательные моменты. При апробации этих подходов в отборе корней тригонометрического уравнения, понимаешь, что каждый из этих способов удобен по-своему в том или ином случае. Например, алгебраический способ (решение неравенством) наиболее эффективен, когда промежуток для отбора корней достаточно большой, в тоже время он дает практически стопроцентное нахождение целочисленного параметра для вычисления корней, а применение арифметического способа приводит к громоздким вычислениям. При отборе корней уравнения, удовлетворяющих дополнительным условиям, т.е. когда корни уравнения принадлежат заданному промежутку, мне проще и нагляднее получить корни с помощью тригонометрической окружности, а проверить себя можно арифметическим способом. Замечу, что при решении тригонометрических уравнений трудности, связанные с отбором корней, возрастают, если в уравнении приходится учитывать ОДЗ. Как показывает практика и анкетирование моих одноклассников, из четырёх возможных методов отбора корней тригонометрического уравнения по дополнительным условиям, наиболее предпочтительным является отбор корней по окружности. Анкетирование проходили 12 респондентов, изучающих тригонометрию (прил. №5). Большинство из них отвечали, что этот раздел математики достаточно сложный: большой объем информации, очень много формул, табличных значений, которые нужно знать и уметь применять на практике. Еще как одна из проблем — небольшое количество времени, отведенное на изучение этого сложного раздела математики. И я разделяю их мнение. При такой сложности, многие считают, что тригонометрия важный раздел математики, который находит применение в других науках и практической деятельности человека.

СПИСОК ЛИТЕРАТУРЫ

1. Математика: алгебра и начала математического анализа, геометрия. Алгебра и начала математического анализа. 10 класс: учеб для общеобразоват. организаций: базовый и углубленный уровни/ [С.М.Никольский, М.К.Потапов, Н.Н.Решетников и др.]-3 -е изд.- М.: Просвещение, 2016.
2. Алгебра и начала математического анализа: Учеб для 10-11 кл.общеобразоват. организаций / А.Н.Колмогоров, А.М.Абрамов, Ю.П.Дудницин и др. под редакцией А.Н.Колмогорова — М. Просвещение, 2017.
3. С.В Кравцев и др. Методы решения задач по алгебре: от простых до самых сложных — М: Издательство: «Экзамен», 2005.
4. Корянов А.Г., Прокофьев А.А. — Тригонометрические уравнения: методы решения и отбор корней. — М.: Математика ЕГЭ, 2012.

Способы отбора корней в тригонометрических уравнениях

Тригонометрия традиционно относится к наиболее трудному для школьников материалу. Главной причиной этой трудности является большое количество формул и различных фактов, которые школьники должны не только помнить наизусть, но и уметь гибко и широко варьировать их применимость. Проблема отбора корней, отсеивания лишних корней при решении тригонометрических уравнений специфична.

При отборе корней в процессе решения тригонометрических уравнений обычно используют один из следующих способов: арифметический, алгебраический, геометрический, функционально- графический.

Просмотр содержимого документа
«Способы отбора корней в тригонометрических уравнениях»

Способы отбора корней в тригонометрических уравнениях

Болотина Татьяна Гавриловна МКОУ « Возовская СОШ» Поныровского района,

Способы отбора корней в тригонометрических уравнениях

а) непосредственная подстановка полученных корней в уравнение и имеющиеся ограничения;

б) перебор значений целочисленного параметра и вычисление корней.

а) решение неравенства относительно неизвестного целочисленного параметра и вычисление корней;

б) исследование уравнения с двумя целочисленными параметрами.

а) изображение корней на тригонометрической окружности с последующим отбором и учетом имеющихся ограничений;

б) изображение корней на числовой прямой с последующим отбором и учетом имеющихся ограничений.

выбор корней с помощью графика простейшей тригонометрической функции.

Арифметический способ (непосредственная подстановка полученных корней в уравнение и имеющиеся ограничения)

Найдите корни уравнения cos x = 0,5, удовлетворяющие неравенству sin x ≤ 0.

cos x = 0,5, x = + 2πn, n ϵ Z,

Проверим выполнение условия sin x ≤ 0.

Для x = + 2πn, n ϵZ,sin= sin =

Первая серия корней является посторонней.

Для x = — + 2πn, n ϵ Z,sin= sin=.

Ответ: x = + 2πn, n ϵ Z

а) Решите уравнение .

б) Найдите все корни этого уравнения, принадлежащие отрезку .

а) Решая квадратное уравнение относительно sin, находим,

Запишем решение уравнения в виде:

б) Рассмотрим отбор корней на отрезке

• Арифметический способ

Перебирая значения переменной, обозначающей целые числа, мы должны добиться того, чтобы найти все точки внутри промежутка и по одной точке слева и справа от данного промежутка.

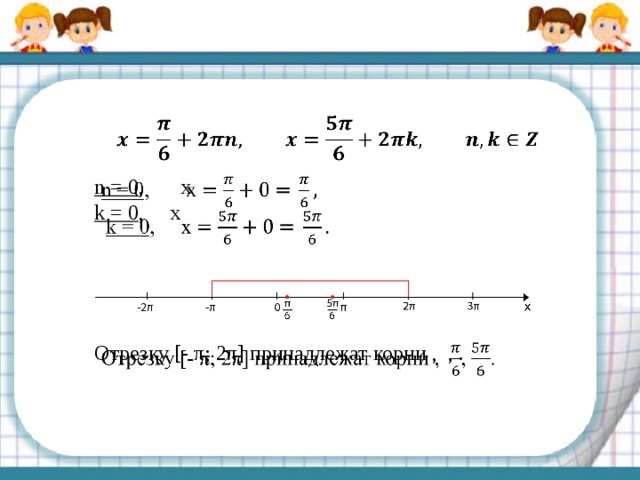
Пусть x = + 2πk, k ϵ Z.

при k = -1, x=- ∉ [- π; 2π]

при k = 1, x=∉ [- π; 2π]

Пусть x = + 2πn, n ϵ Z.

при n= -1, x= — ∉ [- π; 2π]

при n = 0, x = ϵ [- π; 2π]

при n = 1, x = ∉ [- π; 2π]

Отрезку [- π; 2π] принадлежат корни , .

Пусть x = + 2πn, n ϵ Z.

при n = -1, x= — = -330 ° ∉ [- π; 2π]

при n = 0, x = = 30° ϵ [- π; 2π]

при n = 1, x = =390 ° ∉ [- π; 2π]

Пусть x = + 2πk, k ϵ Z.

при k = -1, x=- = -210 ° ∉ [- π;2π]

при k = 1, x== 510 ° ∉ [- π; 2π]

Отрезку [- π; 2π] принадлежат корни ,

Рассмотрим отбор корней с помощью координатной прямой.

Покажем дополнительные точки, которые находятся внутри отрезка [- π; 2π], слева и справа от него

Отрезку [- π; 2π] принадлежат корни , , .

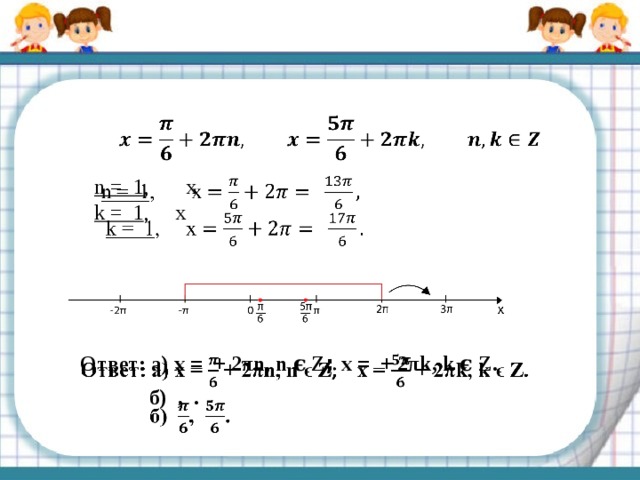
Ответ: а) х = + 2πn, n ϵ Z ; х = + 2πk, k ϵ Z.

2. Алгебраический способ .

Корни уравнения должны принадлежать отрезку [- π; 2π].

Это значит, что – π ≤ x ≤ 2π.

Пусть x = + 2πk, k ϵ Z.

Пусть x = + 2πn, n ϵ Z

Тогда – π ≤ + 2πk ≤ 2π;

Тогда – π ≤ + 2πn ≤ 2π;

Отрезку [- π; 2π] принадлежат корни , .

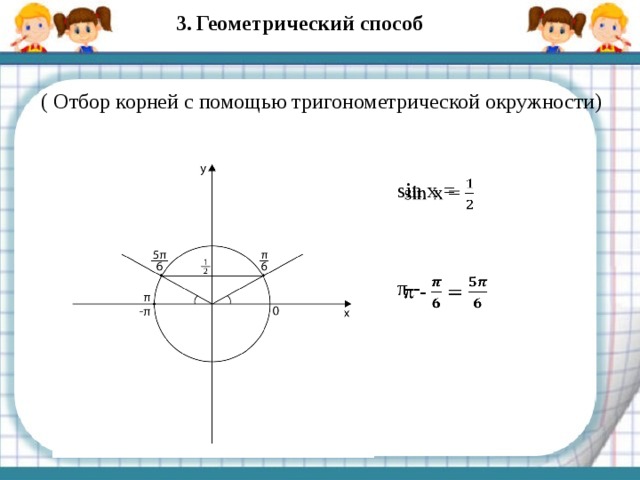
3. Геометрический способ

( Отбор корней с помощью тригонометрической окружности)

3. Геометрический способ

( Отбор корней с помощью тригонометрической окружности)

Отрезку [- π; 2π] принадлежат

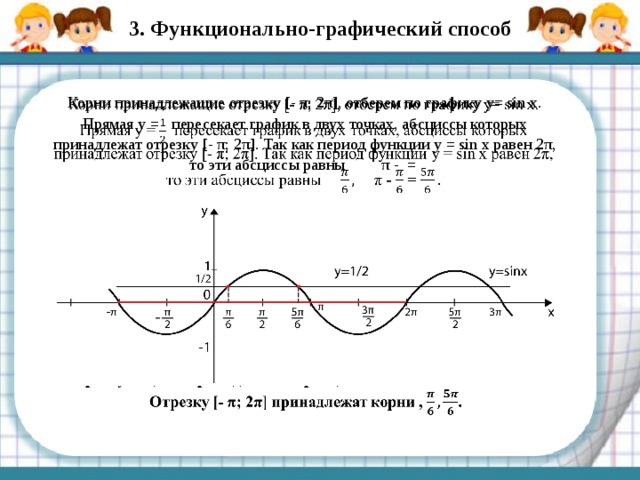
3. Функционально-графический способ

Корни принадлежащие отрезку [- π; 2π], отберем по графику y= sin x. Прямая y = пересекает график в двух точках, абсциссы которых принадлежат отрезку [- π; 2π]. Так как период функции y = sin x равен 2π, то эти абсциссы равны π — =

Отрезку [- π; 2π] принадлежат корни , .

а) Решите уравнение 2sin 4 x + 3 cos 2x + 1 = 0

б) Найдите все корни этого уравнения, принадлежащие отрезку [π; 3π]

2 sin 4 x + 3(1 – 2sin 2 x) +1 = 0

2 sin 4 x – 6 sin 2 x + 4 = 0

sin 4 x – 3 sin 2 x + 2 = 0, сделаем замену.

t 2 – 3 t 2 + 2 = 0

По теореме Виета или через дискриминант

t 1 = 1 или t 2 = 2

sin 2 x = 1 или sin 2 x = 2

sinx = ±1 или sinx = ± — уравнение корней не имеет

Отбор по окружности. На числовой окружности нужно показать нужный нам отрезок.

Отберем все точки которые попадают на этот отрезок

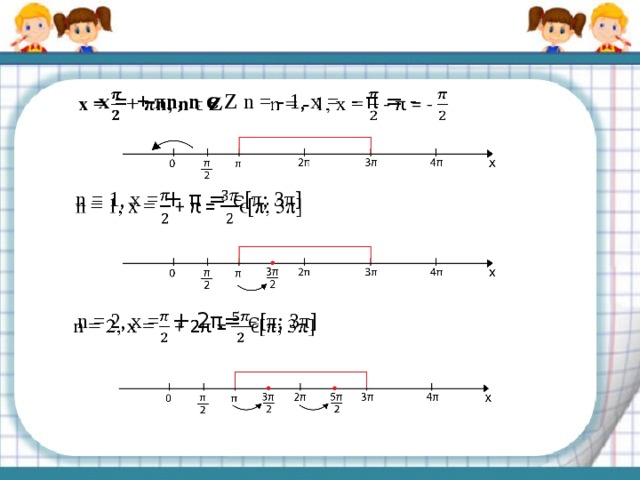
Рассмотрим отбор корней с помощью координатной прямой.

Покажем дополнительные точки, которые находятся внутри отрезка [π; 3π] , слева и справа от него

x = + πn, n ϵ Z n = — 1, x = — π = —