Геометрическое решение системы уравнений и неравенств

Методическая разработка урока: «Геометрический метод решения уравнений, неравенств, систем»
методическая разработка по алгебре (10 класс)

Внесение геометрического метода в алгебраические уравнения, неравенства, системы для их рационального решения

Скачать:

Предварительный просмотр:

Технологическая карта урока

Тема урока : Геометрический метод решения уравнений, неравенств, систем.

Тип урока: Урок общеметодологической направленности.

Цели урока: Внесение геометрического метода в алгебраические уравнения, неравенства, системы для их рационального решения.

— формировать у учащихся представления о методах, связывающих изучаемые понятия в единую систему;

— организовать учебную деятельность учащихся на саморазвитие и рефлексивную самоорганизацию;

— воспитать личностную позицию для решения сложных задач.

Образовательные ресурсы: задачи из сборников ЕГЭ (часть С), карточки.

Форма : комбинированный урок.

Метод обучения: по характеру мыслительной деятельности и познавательной активности — проблемно-поисковый.

Основные термины и понятия : геометрический метод решения, уравнения, неравенства, система.

Планируемые образовательные результаты:

— формирование целостного мировоззрения на математику, соответствующего современному уровню развития;

— развитие готовности к решению творческих задач, умения находить адекватные способы поведения и взаимодействия с партнёрами во время учебной деятельности.

— умение выделять альтернативные способы достижения цели и выбирать наиболее эффективный способ, для осуществления познавательной рефлексии в отношении действий по решению учебных и познавательных задач;

— понимание проблемы, умение ставить вопросы, выдвигать гипотезу, давать определения понятиям;

— умение на практике пользоваться основными логическими приёмами, методами объяснения, решения проблем, прогнозирования и др.;

— развитие способности к анализу, сравнению математических методов решения задач;

-создание основы для формирования интереса к расширению и углублению знаний по предмету.

Проектная работа по математике «Геометрическое решение алгебраических задач»

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

«Актуальность создания школьных служб примирения/медиации в образовательных организациях»

Свидетельство и скидка на обучение каждому участнику

МКОУ «Богучарский лицей»

«Геометрические решения алгебраических задач»

Выполнила: Мануйлова Валентина ученица 10 физико-математического/социально-экономического класса

Руководитель: учитель математики ВКК Кобелева Татьяна Васильевна.

Глава 1 Немного истории

Глава 2. Геометрические методы решения алгебраических задач

2.1. Решение алгебраических задач с помощью теоремы Пифагора

2.2. Применение в решении задач теоремы, обратной теореме Пифагора

2.3. Геометрическое решение текстовых задач

Глава 3. Задачи с практическим компонентом

Глава 4. Геометрическое решение уравнений и систем уравнений

4.1. Решение квадратного уравнения с помощью циркуля и линейки

4.2. Графический способ решения алгебраических систем уравнений и уравнений с модулем.

4.3. Решение некоторых типов тригонометрических задач геометрическим способом

Глава 5. Геометрическое решение некоторых нестандартных задач

«Но когда эти науки (алгебра и геометрия) объединились, они энергично поддержали друг друга и быстро зашагали к совершенству.» (Ж. Л. Лагранж)

В классическую древнюю эпоху геометрия занимала привилегированное положение. Она являлась основной наукой, в которой проявлялось искусство доказательства. Суть геометрического метода состоит в том, что решение задачи и доказательство направляется наглядным представлением. Например, в старинных индийских сочинениях доказательство сводилось к чертежу, подписанному одним словом «Смотри!». У древних греков величины обозначались не числами или буквами, а отрезками прямых. Они говорили не « a 2 », а «квадрат на отрезке а», не « ab », а «прямоугольник, содержащийся между отрезками a и b ». Некоторые термины подобного геометрического изложения алгебры сохранились до сих пор. Так, мы называем вторую степень числа квадратом, а третью степень – кубом числа. Решая алгебраические задачи, мы порой не задумываемся, что их можно решить геометрическим способом, может даже более простым, рациональным и наглядным.

Актуальность темы состоит в необходимости связи алгебры и геометрии, как элементов, составляющих одно целое – науку математику, а также в применении знаний геометрии в жизни. Данная тема интересна, потому что она позволяет находить новые неординарные подходы к решению задач. Многие задачи алгебры очень трудно решить аналитическим путем. Поэтому любое представление условия задачи в виде рисунка или чертежа облегчает решение задачи. Геометрический метод состоит в том, что само доказательство или решение задачи направляется наглядным представлением.

Цель работы: рассмотреть различные геометрические методы в решении алгебраических задач.

1) показать, что преимущество геометрического решения алгебраических задач в его наглядности, так как геометрический подход допускает изящное решение;

2) рассмотреть применение теоремы Пифагора и обратной ей теоремы для решения алгебраических задач;

3) рассмотреть применение метода линейных и двумерных диаграмм для решения алгебраических задач;

4) продемонстрировать применение геометрического метода для решения текстовых задач.

Глава 1. Немного истории

В наши дни трудно найти человека, у которого геометрия не ассоциировалось бы с теоремой Пифагора. Причина такой популярности теоремы Пифагора триедина: простота, красота и значимость. В современных учебниках теорема сформулирована так: «В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов»

о мнению известного немецкого историка математики Кантора, равенство 3 2 +4 2 =5 2 было известно уже египтянам еще около 2300 г. до н. э. во времена царя Аменемхета I (согласно папирусу 6619 Берлинского музея). Кантор писал, что гарпедонапты, или «натягиватели веревок», строили прямые углы при помощи прямоугольных треугольников со сторонами 3, 4 и 5 .Очень легко можно воспроизвести их способ построения. Возьмем веревку длиною 12 м и привяжем к ней по цветной полоске на расстоянии 3 м от одного конца и 4 м от другого. Прямой угол окажется заключенным между сторонами длиной в 3 и 4 м (рис. 1). Решим задачу из «Арифметики» Магницкого, по которой начинал свой путь в науку Михайло Ломоносов.

«Случилося некому человеку к стене лестницу прибрати, стены же тоя высота есть 117 стоп. И обреете лестницу долготью 125 стоп. И ведати хочет, колико стоп сея лестницы нижний конец от стены отстояти имать»

Решение: Пусть х- расстояние от лестницы до стены (рис. 2).

П

о теореме Пифагора: 117 2 + х 2 =125 2

х 2 =1936; х=44 , так как х>0

Задача из китайской «Математики в девяти книгах». Имеется водоем со стороной в 1 чжан = 10 чи. В центре его растет камыш, который выступает над водой на 1 чи. Если потянуть камыш к берегу, то он как раз коснётся его. Спрашивается: какова глубина воды и какова длина камыша?

Решение: Пусть х — искомая глубина, тогда х+1 — длина камыша.

По теореме Пифагора: 5 2 +х 2 =(х+1) 2 , х=12

Ответ: глубина воды 12 чи, длина камыша 13 чи.

Задача о бамбуке из древнекитайского трактата «Гоу-гу». Имеется бамбук высотой в 1 чжан. Вершину его согнули так, что она касается земли на расстоянии 3 чи от корня (1 чжан = 10 чи).

Какова высота бамбука после сгибания?

Решение: Пусть х — высота бамбука после сгибания. Тогда 10-х — вершина бамбука, которую согнули.

По теореме Пифагора: (10-х) 2 =х 2 +3 2

Ответ: 4 11 /₂₀ чи — высота бамбука после сгибания.

Задача «О лотосе» из Египта. На глубине 12 футов растет лотос с 13-футовым стеблем. Определите, на какое расстояние цветок может отклониться от вертикали, проходящей через точку крепления стебля ко дну.

х=

Ответ: на 5 футов.

Задача Бхаскари из Индии.

На берегу реки рос тополь одинокий.

Вдруг ветра порыв его ствол надломал.

Бедный тополь упал. И угол прямой

С теченьем реки его ствол составлял.

Запомни теперь, что в этом месте река

В четыре лишь фута была широка

Верхушка склонилась у края реки.

Осталось три фута всего от ствола,

Прошу тебя, скоро теперь мне скажи:

У тополя как велика высота?

По теореме Пифагора 3 2 +4 2 =5 2

Ответ: высота тополя равна 5 футам.

Глава 2 Геометрические методы решения алгебраических задач

2.1 Решение алгебраических задач с помощью теоремы Пифагора

Теперь решим некоторые алгебраические задачи с помощью теоремы Пифагора.

Задача 1. Решите уравнение .

Решение: Рассмотрим прямоугольный треугольник, у которого гипотенуза с равна 13, катет а равен 12, а другой катет х — неизвестен. Тогда алгебраическая задача «Решите уравнение » получает геометрическую интерпретацию: «Найдите катет х прямоугольного треугольника, если его гипотенуза равна 13, а другой катет равен 12». В результате получаем |х|=5, а значит, х=±5. Ответ: х=±5.

Задача 2. Решите систему уравнений при условии, что x, y, z и t – положительны:

ешение: Рассмотрим прямоугольные треугольники с гипотенузами 1, 2, 3 и 4 и катетами x, у, z и t соответственно. Расположим эти треугольники на чертеже в виде «цепочки» так, чтобы их катеты были соответственно параллельны (рис. 4 a ). Проведя дополнительные построения, получим треугольник AВС с прямым углом С (рис. 4 b ), у которого катет АС = 8, поскольку сумма длин соответствующих катетов , , , равна 8. Катет ВС = 6, так как x + у + z + t = 6. тогда гипотенуза АВ = =10. Отсюда следует, что гипотенузы рассматриваемых треугольников лежат на одной прямой, потому что в противном случае длина ломаной AFEDB была бы строго больше 10.Точки F, E и D делят гипотенузу АВ на части, которые относятся следующим образом BD:DE:EF:FA = 1:2:3:4. Проведем через эти точки прямые, параллельные катету АС. По теореме о пропорциональных отрезках катет ВС разделился в том же отношении, т.е. x:y:z:t = 1:2:3:4. Следовательно, x = 0,6, y = 1,2, z = 1,8, t = 2,4.

2.2 Применение в решении задач теоремы, обратной теореме Пифагора

Мы знаем, что теорема Пифагора имеет несколько сотен доказательств, и ею очень часто пользуются при решении задач, в то время как обратная ей теорема: «Если квадрат одной стороны треугольника равен сумме квадратов двух других сторон, то треугольник прямоугольный» — не имеет столько доказательств, но является не менее важной. Теорема, обратная теореме Пифагора, помогает в решении некоторых алгебраических задач.

Рассмотрим простую на первый взгляд задачу с неожиданным ответом.

Задача 3. Следует ли из теоремы Пифагора, что треугольник со сторонами 6, 8, 10 прямоугольный?

Решение: Нет. Треугольник со сторонами 6, 8, 10, конечно, прямоугольный, но это следует не из теоремы Пифагора, а из теоремы ей обратной: если а 2 + b 2 =с 2 то, угол С=90°.

Задача 4. Из условий х 2 +у 2 =9, у 2 + z 2 =16 и у 2 =х z для положительных х, у, z , не вычисляя их значений, указать значение выражения ху+у z

Решение: По теореме, обратной теореме

Пифагора, числа х, у и 3 являются соответственно длинами катетов и гипотенузы треугольника АВ D с прямым углом D . А рассмотрев второе уравнение системы, можно сделать вывод, что у, z и 4 так же

есть соответственно длины катетов и гипотенузы треугольника ВС D

с прямым углом D . Третье уравнение системы разрешает

тверждать, что число у есть среднее пропорциональное чисел х и z ,

и по теореме, обратной теореме о пропорциональных отрезках в

прямоугольном треугольнике, угол АВС – прямой (рис. 5). Теперь рассмотрим выражение ху+у z =(х+ z )у= 2 S _{A ВС}=3·4=12.

Задача 5. Решить систему уравнений:

По теореме, обратной теореме Пифагора, из уравнения х 2 + у 2 =3 2 , числа х и у являются катетами АBD ( D – прямой) с гипотенузой АВ = 3. Рассматривая второе уравнение у 2 + z 2 = 16, построим BDC, где у и z – катеты, а ВС = 4 – гипотенуза. Третье уравнение y 2 = xz подсказывает, что число у есть среднее пропорциональное чисел х и z.

По теореме обратной теореме о пропорциональных отрезках 0 АС = ( х + z ) = = 5, тогда

AB 2 = AD • AC, 9 = х • 5, х =9/5

BC 2 = DC • AC, 16 = z • 5, z = 16/5

BD 2 = y 2 = x • z = 9/5 • 16/5 и BD =12/5 = y.

Однако, такой прием дает потерю корней, легко убедиться, что х = ± 9/5; у = ± 12/5; z = ± 16/5.

2.3 Геометрическое решение текстовых задач

Очень многие текстовые задачи на составление уравнений (или систем уравнений) можно решать графически. К ним относятся задачи на движение и на совместную работу. Решение задачи основывается на точных геометрических соотношениях. Преимущество геометрического решения в его наглядности, так как чертёж помогает глубже понять условия задачи.

Задача 6. В одном элеваторе было зерна в два раза больше, чем в другом. Из первого элеватора вывезли 750 т зерна, во второй элеватор привезли 350 т, после чего в обоих элеваторах зерна стало поровну. Сколько зерна было первоначально в каждом элеваторе?

Р

ешаем данную задачу с помощью линейной диаграммы (рис. 6). Построенная линейная диаграмма превращает алгебраическую задачу в геометрическую, решение которой основано на использовании свойств длины отрезка, а именно: 1) равные отрезки имеют равные длины; меньший отрезок имеет меньшую длину; 2) если точка делит отрезок на два отрезка, то длина всего отрезка равна сумме длин этих двух отрезков.

Решение: AB = 2CD — первоначальное распределение зерна между двумя элеваторами; BK = 750, DE = 350. AK = CE — конечное распределение зерна между элеваторами.

CD=AF=FB (по построению), FB= 350 + 750 = 1100, тогда CD=1100, AB = 1100·2 = 2200.

Ответ: 2200 т, 1100 т.

З

адача 7. Предприятие уменьшило выпуск продукции на 20% . На сколько процентов необходимо теперь увеличить выпуск продукции, чтобы достигнуть его первоначального уровня.

Решение: Представим первоначальный выпуск продукции в виде отрезка АВ (рис. 7). Разделим его на 5 равных частей и отметим точку С на расстоянии 1/5 от В. Мы получим отрезок АС, равный 4/5 АВ. Из чертежа видно, что требуется найти какую часть составляет ВС от АС. Решение очевидно. Так как ¼ АС =ВС, тогда требуется увеличить выпуск продукции на ¼ АС, т. е. на 25%. Ответ: на 25%.

Задача 8. Бригада лесорубов ежедневно перевыполняла норму на 16 м 3 , поэтому недельную норму (шесть рабочих дней) она выполнила за четыре дня. Сколько кубометров леса заготовляла бригада в день?

Так как в задаче рассматривается произведение двух величин (A = p·n), то для наглядности представим его в виде двумерной диаграммы. Двумерная диаграмма — это площадь одного или нескольких прямоугольников, стороны которых изображают численные значения рассматриваемых величин (p и n), а площадь прямоугольника изображает их произведение (S = A).

Решение: Пусть S_ABCD определяет недельную норму бригады лесорубов. AB — производительность (м 3 ) бригады в день по плану; AD — количество дней; S_AMNK — объем работы, выполненный бригадой за четыре дня (рис. 8).

S _AMNK = S _ABCD = S; S ₁ = S ₂ , так как S ₁ + S ₃ = S ₂ + S ₃ . S ₁ = 2KE, S ₂ = =16·4 = 64, значит 2KE = 64, тогда KE = 32. AB = KE = 32, AM = AB + BM = 32 + 16 = 48.

Ответ: бригада заготовляла в день 48 м 3 леса.

Итак, метод длин и диаграмм является одним из удобных, интересных и наглядных способов, позволяющих лучше понять условие и решить задачу на этапе чертежа.

Расстояние между двумя городами равно 450 км. Два автомобиля выходят одновременно навстречу друг другу. Один автомобиль мог бы пройти все расстояние за 9 часов, другой – вдвое быстрее. Через сколько часов они встретятся?

Читаем с чертежа ответ: 3 часа.

Задача 10. На двух типографских станках, работающих одновременно, можно сделать копию пакета документов за 10 минут. За какое время можно выполнить эту работу на каждом станке в отдельности, если известно, что на первом ее можно сделать на 15 минут быстрее, чем на второй?

Р

ешение: Н а оси абсцисс откладываем время работы станков в минутах. Оба станка сделают работу вместе за 10 минут. ОМ=10. Тогда одной первой понадобится t минут. А второй ( t +15) минут. V — объем работ, который нужно выполнить. ОВ — график работы первого станка, ОС — второго, ОА – вместе (рис. 9). ΔО VB ≅Δ NAB и Δ OP С≅ΔOMK, откуда VO / AN = VB / AB и С P / KM = OP / OM ; покажем, что AN = KM . Так как за 10 минут первый станок выполнит часть работы, соответствующий отрезку NM ( AN — отрезок работы который выполнит второй станок). Но за 10 минут второй станок выполнит часть работы, соответствующую МК. Поэтому А N =КМ. Учитывая это равенство и то, что СР= VO , получаем, VO/AN=CP/KM. Так как VO / AN = VB / AB и С P / KM = OP / OM , то получаем соотношение: VB / AB = OP / OM , значит t /( t -10)=( t +15)/10; t 2 -5 t -150=0; t =15 Таким образом, I станок выполнит работу за 15 минут, а II за 30 минут.

Ответ: 15 минут, 30 минут.

Задача 11. Два велосипедиста выезжают одновременно из пунктов А и В навстречу друг другу. Один прибывает в В через 27 минут после встречи, а другой прибывает в А через 12 минут после встречи. За сколько минут проехал каждый велосипедист свой путь?

ешение: Рассмотрим две системы координат tAy и t _’ By _’ (рис. 10). На оси А t откладываем время движения первого велосипедиста, а на оси В t _’ – время движения второго велосипедиста. Оси А t и Bt _’ сонаправлены. Оси пройденного пути противоположно направлены, длина отрезка АВ в каждом случае равна пройденному пути. Отрезок АВ₁ – график движения первого велосипедиста, а отрезок ВА₁ – график движения второго. Точка О соответствует моменту их встречи. Время движения до встречи обозначим t . ΔВ₁ОМ подобен ΔАО N , ΔМОВ подобен ΔNOA₁. Тогда MB ₁/ AN = MO / ON и BM / NA ₁= MO /О N . Из равенства следует: 27/ t = t /12, откуда t =18. Таким образом, первый велосипедист проехал весь путь за 18+12=30 (мин.), а второй за 18+27=45 (мин.).

Ответ: 30 минут, 45 минут.

Задача 12.
На двух копировальных машинах, работающих одновременно, можно сделать копию пакета документов за 10 мин. За какое время можно выполнить эту работу на каждой машине в отдельности, если известно, что на первой её можно сделать на 15 мин. быстрее, чем на второй?

Решение: На оси абсцисс откладываем время работы копировальных машин в минутах (рис). Обе машины, работая вместе, сделают копию за 10 мин. (ОМ=10). Тогда одной первой для этого понадобится t мин, а одной второй – (t+15) мин. Положение точки V на оси ординат соответствует объёму работы, которую необходимо выполнить.

Так как объём работы прямо пропорционален затраченному времени, то график работы копировальных машин представляют собой отрезки: ОВ – график работы первой, ОС – график работы второй, ОА – график совместной работы.

Рассмотрим две пары подобных треугольников ОСР и ОКМ
Покажем, что AN=KM. За 10 мин. первая машина выполнит часть работы, соответствующую отрезку NM (AN – отрезок работы, который выполнит вторая машина). Но за 10 мин. Вторая машина выполнит часть работы, соответствующую MK. Поэтому AN=KM. Учитывая это равенство и то, что CP=VO, получаем = . Из пропорций (1) и (2) получаем соотношение: = , из которого легко перейти к уравнению =

Решая это уравнение, находим положительный корень t = 15. Таким образом, первая машина сделает копию пакета документов за 15 мин, а вторая – 30 мин.

Ответ: 15 мин, 30 мин.

Итак, геометрический метод в решении алгебраических задач отличается быстротой. Мы убедились, что задачи на движение и совместную работу возможно решать с помощью геометрии. И такое решение является неординарным и рациональным, а также позволяет экономить время и быстро находить правильный ответ.

Глава 3 Задачи с практическим компонентом.

Как в прошлом, так и в настоящем для решения практических задач люди использовали знания геометрии. Например, работники некоторой судоверфи часто сталкивались с задачами, которые можно решить с помощью теоремы Пифагора.

Задача 13 Парусное судно стояло на ремонте на судоверфи. Для крепления мачты необходимо было установить 4 троса. Один конец каждого троса должен крепиться на высоте 12 м, другой на земле на расстоянии 5 м от мачты. Хватило ли 50 м троса для крепления мачты? (рис. 11)

Решение: По теореме Пифагора 12 2 +5 2 =144+25=169; 13·4=52 (м)

твет: троса не хватило.

В подтверждение возможности использования теоремы Пифагора на практике мы провели небольшой эксперимент, идея которого возникла во время прочтения книги «Занимательная геометрия» Я. И. Перельмана. Гуляя однажды по лесу в ясный солнечный день, мы заметили две сосны одна в 38 м от другой. Мы решили измерить их высоты. Дождавшись момента, когда длина нашей собственной тени стала равной нашему росту и, измерив длину тени деревьев, мы определили их высоты, используя свойство сторон равнобедренного треугольника. А затем составили и решили следующую задачу.

Высота первой сосны равна 29 м, второй – 4 м. Как велико расстояние между их верхушками?

ешение: Искомое расстояние АВ между верхушками сосен (рис. 12) находится по теореме Пифагора: (29-4) 2 +38 2 =25 2 +38 2 ≈45,5 2

Подобные задачи решаются в различных областях: в судостроении, ракетостроении, машиностроении, строительстве и т.д.

Глава 4 Геометрическое решение уравнений и систем уравнений

4.1Решение квадратного уравнения с помощью циркуля и линейки

В древности, когда геометрия была более развита, чем алгебра, квад­ратные уравнения решали не алгебраически, а геометрически.

Среднеазиатским ученым Мухаммедом ал-Хорезми (IX в.) были рас­смотрены и решены шесть видов квадратных уравнений, но без какого бы то ни было алгебраического формализма (в геометрической форме), содер­жащих в общих частях только члены с положительными коэффициентами, причем рассматривались только положительные корни. Суть его рассуж­дений видна из рисунка (он рассматривает уравнение х 2 + 10 x= 39 ).

Площадь большого квадрата скла­дывается из площади х 2 + 10x, равной левой части рассматриваемого урав­нения, и площади четырех квадратов со стороной 5/2, равной 25.

S_ABCD =х 2 + 10x + 25 = 39 + 25 = 64; отку­да следует, что сторона квадрата ABCD, то есть отрезок АВ= 8, а ис­комая сторона первоначального квадрата равна

Нахождение корней квадратного уравнения с помощью циркуля и линейки

Следует упомянуть и о на­хождении корней квадратного уравнения ах 2 + вх + с=О с по­мощью циркуля и линейки.

До­пустим, что искомая окружность пересекает ось абсцисс в точках B(x₁;0) и D(x₂;0), где х₁ и х₂ — корни уравнения ах 2 + вх + с =0, и проходит через точки А(0; 1) и С(0;у) на оси ординат. Тогда по теореме о секущих имеем

ОВ * OD = О А * ОС, откуда

Центр окружности находится в точке пересечения перпендикуляров SF и SK, восстановленных в серединах хорд АС и BD, поэтому

координаты точки S

Итак:1)построим точки S; (центр окружности) и A(0;1);

2) проведем окружность радиуса SA;

3) абсциссы точек пересечения этой окружности с осью Ох являют­ся корнями исходного квадратного уравнения.

При использовании данного метода также возможны три случая (рис. 3):

Уравнения степеней выше второй тоже решали геометрически при помощи кривых — гиперболы, параболы и др.

Нахождение корней квадратного уравнения с помощью циркуля и линейки

Задача 15 . Решить квадратное уравнение 7х 2 -6х-1=0.

1) Построим точки S (-b/2a; (a+c)/2a) =S(3/7; 3/7) — центр окружности и А(0;1) на координатной плоскости;

2) Проведем окружность радиуса SA (рис. 4);

3) Окружность пересекает ось абсцисс в точках (-1/7;0) и (1;0)

4) Проверкой убеждаемся, что х₁=−1/7; х₂=1 – корни данного уравнения

4.2 Графический способ решения алгебраических систем уравнений и уравнений с модулем.

Графический способ часто эффективно используется для решения уравнений, систем уравнений и неравенств. На геометрическом языке решить систему уравнений – значит найти все общие точки графиков уравнений, входящих в систему. А решить неравенство — значит найти множество точек координатной плоскости, удовлетворяющих его условию. Графический метод изучается в курсе алгебры, но он основан на использовании геометрических представлений функций и связанных с ними законов геометрии.

Задача 16. Решить уравнение: |x-1|+2x-5=0.

Запишем уравнение в виде lx -1=5-2х . Так как |x – 1| ≥ 0 при любых х, то и 5 – 2x ≥ 0 , т. е. x ≤ 2,5. Построим графики функций у₁=|x-1|, y₂=5-2x (рис. 5).

Решением данного уравнения является абсцисса точки пересечения данных графиков.

Задача 17. Сколько корней имеет система

Решение: Преобразуем все три уравнения системы:

Итак, данная система принимает вид:

График первого уравнения – окружность с центром в точке (-4;6) и радиусом 10; график второго – парабола, полученная из параболы х=-у2 путем параллельного переноса в точку (13;3); график третьего уравнения окружность с центром в точке (8;3) и радиусом 5. Построив эти графики, мы находим единственное решение системы (4;0) (рис. 6).

4.3Решение некоторых типов тригонометрических задач геометрическим способом

Известно, что основные тригонометрические тождества и формулы приведения выведены с использованием теорем геометрии: теоремы Пифагора, признаков равенства треугольников, признаков подобия треугольников и других теорем.

В основе идеи применения геометрии при решении тригонометрических задач лежит то обстоятельство, что тригонометрические функции y = sin x , y = cos x , y = tg x , y = ctg x определяются при непосредственном участии геометрии.

Вычисление значений тригонометрических функций по заданному значению одной из них геометрическим способом без применения формул основных тригонометрических тождеств. Такие вычисления можно выполнять для углов любой четверти.

Задача 18. Дано: sin x = , 0°≤ α ≤ 90°

Найти cos α , tg α .

Т. к. α принадлежит I четверти, то cos α > 0.

cos α = = = = = .

tg α = = ÷ = = .

Ответ: cos α = , tg α = .

Т. к. sin α = , то пусть противолежащий углу α катет равен 3а, где а – отрезок единичной длины, тогда гипотенуза равна 4а. По теореме Пифагора найдём второй катет:

АС = = = а.

Значит, cos α = = = ,

tg α = = = = .

Ответ: cos α = , tg α = .

Задача 19 . Дано: cos α = — , 180° α

Найти sin α, tg α , ctg α.

Т. к. α принадлежит III четверти, то sin α tg α > 0, ctg α > 0.

sin α = — = — = — ;

tg α = — ÷ = ;

ctg α = = .

Ответ : sin α = — , tg α = , ctg α = .

Вычислим значение sin α , tg α и ctg α для случая, когда угол α – острый, а знак выражения sinα , tg α , ctg α определим в соответствии с четвертью, которой угол α принадлежит.

Т. к. cos α = , то пусть прилежащий к углу α катет будет равен 3а, где а – отрезок единичной длины, тогда гипотенуза равна 5а. По теореме Пифагора найдём второй катет = = = 4а. Тогдп sin α = = , tg α = = , ctg α = = . С учётом того, что α принадлежит третьей четверти, имеем sin α = — , tg α = , ctg α = .

Ответ: sin α = — , tg α = , ctg α = .

Задача 20 . Решить уравнение cos x – sin x = 1.

cos x – sin x = 1

Разделим левую и правую часть уравнения на корень квадратный из суммы квадратов коэффициентов при cos x и sin x , т. е. на = :

× cos x — sin x = .

Заметим , что = sin = cos , т . е . sin × cos x — cos × sin x =

sin =

= arcsin 2 πn , n принадлежит Ζ,

= + 2 πn ,

= 2 πk , k принадлежит Ζ.

= π + 2π m , m принадлежит Ζ,

= + 2π m ,

= — + 2 πl , l принадлежит Ζ .

cos x – sin x = 1

ВС = 1 × sin x = sin x,

АС = 1 × cos x = cos x.

Следовательно, АС – ВС = 1. Но в треугольнике АВС каждая сторона больше разности двух других сторон, т. е. АВ > АС – ВС АС – ВС

если АС = 1, а ВС = 0, т.е. = 0 + 2 πk , = 2 πk , k принадлежит Ζ

если АС = 0, а ВС = 1, т.е. = — + 2 πl , l принадлежит Ζ

Ответ: 2 πk ; — + 2 πl , k , l принадлежат Ζ.

Задача21 . Решить уравнение: arcsin x + arcsin 2 x =

Пусть arcsin x = α, arcsin 2 x = β.

α + β =

sin α = x , sin β = 2 x . Заметим, что x > 0 (иначе arcsin x arcsin 2 x

Пусть АС = 1, АВС D – прямоугольник, тогда ВС = 1 × sin α = sin α = x ,

CD = 1 × sin β = sin β = 2 x

По теореме Пифагора из треугольника АВС:

+ = ,

+ = 1,

5 = 1,

=

x = , x = — — не подходит по условию задачи.

Ответ: .

Задача 22 . Решить уравнение: sin x + cos x = 1.

Воспользуемся формулой sin x + cos x = cos ( x — ).

cos ( x — ) = 1,

cos ( x — ) = ,

— = — +2 πn , n принадлежит Ζ — = + 2 πn ,

= 2 πn , n принадлежит Ζ = + 2 πn , n принадлежит Ζ.

Ответ: 2 πn ; + 2 πn , n принадлежит Ζ.

sin x + cos x = 1.

Из треугольника АВС:

ВС = 1 × sin x = sin x ,

АС = 1× cos x = cos x.

Для любого значения угла x от 0° до 90° в треугольнике АВС АВ πn , = + 2 πn , n принадлежит Ζ.

Ответ: 2 πn ; + 2 πn , n принадлежит Ζ.

Задача 23:_{Вычислить без калькулятора и таблиц sin 18°.}

_{Решение:}

Рассмотрим сектор ОАВ окружности с центром в точке О и радиуса 1, AOB =36 _{º (рис}.10). Тогда ОАВ= = OBA =72°. Проведем хорду АВ, на отрезке ОВ построим точку С так, чтобы АС=АВ, при этом АСВ= = АВС=72°, а САВ=36°. Таким образом, ОАС=36°, следовательно, ОС=АС.

усть АВ=х, тогда ОС=х, СВ=1-х. Поскольку АС — биссектриса треугольника ОАВ, справедлива пропорция , откуда х 2 +х-1=0, (х>0); . По теореме косинусов АВ 2 =ОА 2 +ОВ 2 -2ОА×ОВ× , x 2 =1+1-2 cos 36º, x 2 =2-2 cos 36º, Поэтому . Ответ: .

Глава 5 Геометрическое решение некоторых нестандартных задач

Задачи, встречающиеся на олимпиадах, очень часто требуют нестандартных подходов.

Геометрический метод может помочь в решении таких задач, к которым относятся неравенства, уравнения и системы уравнений с параметрами.

Задача 24. При каком а система уравнений имеет ровно четыре решения?

Решение: Построим линии, определяемые уравнениями системы (рис. 9).

Четыре решения могут быть только в двух случаях, когда a = R₂ =1 или a = r₂ = 1/2 .

Геометрия придает алгебре необыкновенную красоту и изящность. А вместе алгебра и геометрия представляют собой единое целое. Вспомним крылатую фразу французского математика Софии Жермен : «Алгебра – не что иное, как записанная в символах геометрия, а геометрия – это просто алгебра, воплощенная в фигурах» . В ходе работы нам удалось увидеть синтез этих двух великих наук. Мы рассмотрели в работе несколько типов задач, для которых подобрали решение и алгебраическим и геометрическим методами. Сравнили эти решения и попробовали применить данные способы для решения подобных задач. Достигнута цель работы, которая заключается в углубленном изучении математики на основе интеграции алгебраического и геометрического методов решения задач.

В процессе исследования мы решили много исторических, практических, алгебраических задач геометрическими способами. Решения некоторых из них продемонстрированы в работе. Рассматривая различные источники и анализируя литературу, мы пришли к выводу, что алгебраические задачи, которые можно решить геометрически, встречаются очень часто, как на ЕГЭ, так и в школьных учебниках. Мы убедились, что геометрические подходы часто упрощают решение задач. Таким образом, цель работы достигнута.

Преимущества решения задач геометрическим способом:

Графическая иллюстрация облегчает проведение анализа, составления уравнений, помогает найти несколько способов решения.

Расширяется область использования графиков, повышается графическая культура.

Реализуются внутрипредметные (алгебра и геометрия) и межпредметные (математика и физика) связи.

Мы рассмотрели различные задачи, подобрали для них геометрические способы решения, сравнили алгебраический и геометрический методы решения.

Удобнее и нагляднее всего решать геометрическим методом тригонометрические задачи. Этот метод можно использовать в качестве проверки при решении задач.

Рассмотренные геометрические методы подходят для решения конкурсных нестандартных и олимпиадных задач. Позволяют существенно упростить их решение, сделать его более понятным и наглядным.

Применение геометрических методов позволяет развивать пространственное воображение, которое является основным для освоения материала в старших классах. Позволяет сократить время решения задач (применимо к тестам).

Куликова Л. В. , Литвинова С. А., За страницами учебника математики, М. — Глобус, 2008.

Киселева Ю. С., Методическое пособие по теме: Использование геометрических методов при решении алгебраических задач.

В.А. Филимонов, Геометрия помогает решить задачу – Математика в школе № 2-3, 1992

Алгебра: учеб. для 8 кл. общеобразоват. учреждений/ Ю.Н. Макарычев [и др.]; Под ред. С.А. Теляковского. – М.: Просвещение, 2012.

Геометрия, 7-9: учеб. для общеобразоват. учреждений/ Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев и др. – М.: Просвещение, 2012.

Генкин Г.З. Геометрические решения алгебраических задач// Математика в школе. – 2001. – №7.

Единый государственный экзамен. Математика. 11 класс: 2013. – М.: Просвещение.

Жуков А.В. Элегантная математика. Задачи и решения/ А.В. Жуков, П.И. Самолов, М.В. Аппельбаум. – М.: КомКнига, 2005.

За страницами учебника математики/ авт.-сост. С.А. Литвинова. – М.: Глобус, Волгоград: Панорама, 2008.

Математика. 9-11 классы: проектная деятельность учащихся/ авт.-сост. М.В. Величко. – Волгоград: Учитель, 2007.

Перельман Я. И. Занимательная геометрия. – М.: АСТ, 2007.

Энциклопедия для детей. Т. 11. Математика/ Глав. ред. М. Аксенова. – М.: Аванта +, 2007

Электронная энциклопедия «Большая энциклопедия Кирилла и Мефодия».

http://mat.1september.ru/ — Издательский дом «Первое сентября». Учебно-методическая газета «Математика».

http://www.lomonosovo.ru/ — Общественно-информационный сайт «Ломоносово.ру».

Краткое описание документа:

Работа заняла 2 место в Воронежском Государственном Университете на Научно-практической конференции учащихся, секция «Математика» 2014 уч. год.

Актуальность темы состоит в необходимости связи алгебры и геометрии, как элементов, составляющих одно целое – науку математику, а также в применении знаний геометрии в жизни. Поэтому любое представление условия задачи в виде рисунка или чертежа облегчает решение задачи.

Суть геометрического метода состоит в том, что решение задачи и доказательство направляется наглядным представлением.

Цель работы: рассмотреть различные геометрические методы в решении алгебраических задач.

Задачи работы:

1) показать, что преимущество геометрического решения алгебраических задач в его наглядности, так как геометрический подход допускает изящное решение;

2) рассмотреть применение теоремы Пифагора и обратной ей теоремы для решения алгебраических задач;

3) рассмотреть применение метода линейных и двумерных диаграмм для решения алгебраических задач;

4) продемонстрировать применение геометрического метода для решения текстовых задач.

В реферате рассмотрены:

1) исторические задачи, решенные геометрическим способом;

2) задачи на движение с использованием чертежа и подобия треугольников;

3) решение квадратного уравнения с помощью циркуля и линейки;

4) г рафический способ решения алгебраических систем уравнений и уравнений с модулем;

5) р ешение некоторых типов тригонометрических задач геометрическим способом;

6) решение задач с параметром геометрическим способом .

Геометрия придает алгебре необыкновенную красоту и изящность. А вместе алгебра и геометрия представляют собой единое целое. Вспомним крылатую фразу французского математика Софии Жермен : «Алгебра – не что иное, как записанная в символах геометрия, а геометрия – это просто алгебра, воплощенная в фигурах» . В ходе работы нам удалось увидеть синтез этих двух великих наук. Мы рассмотрели в работе несколько типов задач, для которых подобрали решение и алгебраическим и геометрическим методами. Сравнили эти решения и попробовали применить данные способы для решения подобных задач. Достигнута цель работы, которая заключается в углубленном изучении математики на основе интеграции алгебраического и геометрического методов решения задач.
В процессе исследования мы решили много исторических, практических, алгебраических задач геометрическими способами. Решения некоторых из них продемонстрированы в работе. Рассматривая различные источники и анализируя литературу, мы пришли к выводу, что алгебраические задачи, которые можно решить геометрически, встречаются очень часто, как на ЕГЭ, так и в школьных учебниках. Мы убедились, что геометрические подходы часто упрощают решение задач. Таким образом, цель работы достигнута.

Преимущества решения задач геометрическим способом:

• Графическая иллюстрация облегчает проведение анализа, составления уравнений, помогает найти несколько способов решения.
• Расширяется область использования графиков, повышается графическая культура.
• Реализуются внутрипредметные (алгебра и геометрия) и межпредметные (математика и физика) связи.

Выводы

1. Мы рассмотрели различные задачи, подобрали для них геометрические способы решения, сравнили алгебраический и геометрический методы решения.
2. Удобнее и нагляднее всего решать геометрическим методом тригонометрические задачи. Этот метод можно использовать в качестве проверки при решении задач.
3. Рассмотренные геометрические методы подходят для решения конкурсных нестандартных и олимпиадных задач. Позволяют существенно упростить их решение, сделать его более понятным и наглядным.
4. Применение геометрических методов позволяет развивать пространственное воображение, которое является основным для освоения материала в старших классах. Позволяет сократить время решения задач (применимо к тестам).

Геометрический смысл решений неравенств, уравнений и их систем

Рассмотрим решения неравенств.

Теорема 2.3. Множество решений неравенства с двумя переменными

(2.2)

является одной из двух плоскостей, на которые вся плоскость делится прямой , включая и эту прямую, а другую полуплоскость с той же прямой есть множество решений неравенства

(2.3)

Пример 2.4. Построить множество решений неравенства:

а) ; б) .

Решение. В соответствии с теоремой 2.3 множество решений неравенства есть полуплоскость.

а) построим границу полуплоскости – прямую , найдя точки ее пересечения с осями координат A (-4;-0) и B (0;3) на рис. 2.7, a

Для определения искомой полуплоскости (верхней или нижней) рекомендуется задать произвольную контрольную точку, не лежащую на ее границе — построенной прямой. Если неравенство выполняется в контрольной точке, то оно выполняется и во всех точках полуплоскости, содержащей контрольную точку, и не выполняется во всех точках другой полуплоскости. И наоборот, в случае невыполнения неравенства контрольной точке оно не выполняется во всех точках плоскости, содержащей контрольную точку, и выполняется всех точках другой полуплоскости.

В качестве контрольной точки удобно взять начало координат O (0;0), не лежащее на построенной прямой. Координаты точки O не удовлетворяют неравенству: , следовательно, решением данного неравенства является нижняя полуплоскость, не содержащая контрольную точку O. Искомая полуплоскость выделена штриховкой.

б) Построим границу полуплоскости — прямую по двум точкам. Одной из этих точек является начало координат на рис. 2.7,б (в уравнении прямой отсутствует свободный член), а другую точку берем на прямой произвольно, например, А(2;3) на рис. 2.7,б. В качестве контрольной возьмем, например, точку В(1;0). Самую «простую» точку О (0;0) здесь в качестве контрольной брать не следует, ибо она лежит на по­строенной прямой. Так как координаты контрольной точки В(1;0) удовлетворяют неравенству, т.е. , то реше­нием данного неравенства является нижняя (правая) полу­плоскость, содержащая эту точку.

Учитывая, что множество точек, удовлетворяющих уравне­нию (2.4) при n = 3 является плоскостью, а при n > 3 ее обобщением в n -мерном пространстве – гиперплоскостью, можно распрост­ранить теорему 2.3 на случай 3 и более переменных.

Теорема 2.4. Множество всех решений линейного неравен­ства с n переменными 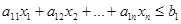является одним из полупространств, на которые все простран­ство делится плоскостью или гиперплоскостью (2.4), включая и эту плоскость (гиперплоскость).

Рассмотрим множество решений системы неравенств.

Теорема 2.5. Множество решений совместной системы т ли­нейных неравенств с двумя переменными

является выпуклым многоугольником (или выпуклой много­угольной областью).

Пример 2.5. Построить множество решений системы неравенств

Решение. Для построения искомого множества решений системы неравенств строим последовательно множество решений каждого неравенства аналогично тому, как это делалось в примере 2.4. Рекомендуем после нахождения каждой полуплоскости и выделения ее соответствующей штриховкой находить последовательно их пересечение: сначала полуплоскостей решений первых двух неравенств (многоугольной области GFD на рис. 2.8), затем первых трех неравенств (треугольника GFD), затем — четырех неравенств (четырехугольника HAFD) затем — пяти неравенств (пятиугольника OAFDE) и наконец всех шести неравенств — выпуклого многоугольника OABCDE.

Рис.2.8

Координаты угловых точек — вершин этого многоугольника найдем как координаты точек пересечения соответствующих прямых. Например, точка D является точкой пересечения прямых II и III, т.е. ее координаты являются решением системы

откуда , т.е. D(9;2). Аналогично находим координаты других угловых точек: O(0;0), A(0;5), B(4/5;6), C(3;6), E(3;0)

При построении областей решении систем неравенств могут встретиться и другие случаи: множество решений — выпуклая многоугольная область; одна точка; пустое множество, когда система неравенств несовместима (рис. 2.9, а, б, в).

Рис.2.9

Теорема 2.6. Множество решений совместной системы m линейных неравенств с n переменными является выпуклым многогранником (выпуклой многогранной областью) в п-мерном пространстве.

Теорема 2.7. Множество всех допустимых решений совместной системы m линейных уравнений с п переменными (т 3) переменными не представляется возможным. В данном случае (когда разность между числом переменных и уравнений n — m = 2) можно поступить так: разобьем все переменные на основные, например х₃ и х₄ (определитель коэффициентов при них отличен от нуля) и неосновные (свободные) переменные х₁ и х₂ и вместо множества решений системы построим множество значений их неосновных переменных (выполнить это возможно, так как их всего две).

С этой целью выразим основные переменные через неосновные:

Так как рассматриваются допустимые значения переменных, т.е. , то

Решениями полученной таким образом системы неравенств (являются точки четырехугольника ABCD на рис. 2.10,б с че­тырьмя угловыми точками А(0; 1), В(0;4), С(6;0), В(l;0).

В данном примере графические построения проведены не в пространстве всех переменных, а в плоскости двух неосновных переменных х₁, х₂. Но так как любой паре неосновных нере­шенных х₁, х₂ соответствуют определенные значения основных переменных х₃, х₄, а следовательно, одно и только одно решение данной системы уравнений, то каждой точке построенного четырехугольника ABCD соответствует одна и только одна точка множества допустимых решений системы уравнений.