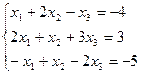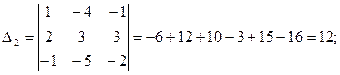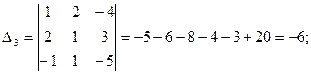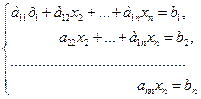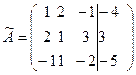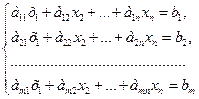ГЛАВА 2. СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ
§ 1. Правило Крамера решения систем линейных уравнений
Определения. Системой линейных уравнений называется система уравнений вида:

Где 



Введем следующие обозначения:


Расширенная матрица, 

Матричными уравнениями называются уравнения вида АХ =В, ХА=В, АХВ=С, где A, B, C – известные матрицы, Х – Искомая.
Матрица 
Лемма. Пусть А – матрица системы (1), а В – столбец ее свободных членов. Тогда система линейных уравнений (1) равносильна матричному уравнению
В следующем смысле: если 

► <



Уравнение (2) называется Матричной формой записи системы (1).
Теорема (правило Крамера). Если в системе линейных уравнений число уравнений равно числу неизвестных и определитель системы 

Где 
►На основании доказанной леммы система (1) равносильна матричному уравнению (2), поэтому теорему доказываем для этого уравнения.
Единственность. Предположим, что (2) имеет два решения 
<




Существование. Покажем, что

Решение уравнения (2). Действительно, 


(4)

Определение. Рангом матрицы называется наивысший порядок отличных от нуля ее миноров. Ранг нулевой матрицы по определению равен нулю. Ранг матрицы будем обозначать так: 
Замечание. Если все миноры K-го порядка матрицы А равны нулю, то все ее миноры (K+1)-го порядка тоже равны нулю. Таким образом, если 
Определение. Элементарными преобразованиями матрицы называются:
1) умножение строк и столбцов на число, отличное от 0;
2) прибавление к какой либо строке (столбцу) другой строки (столбца), умноженной на число;
3) перестановка строк или столбцов.
Лемма. Последнее элементарное преобразование может быть получено последовательным применением первых двух
►Докажем утверждение для строк матрицы. Будем, как и раньше,
Обозначать сокращенно 
Аналогично утверждение доказывается и для столбцов.◄
Теорема. Элементарные преобразования не меняют ранга матрицы.
►Для первого элементарного преобразования утверждение, очевидно, выполняется, так как ранг матрицы зависит от того, будет ли минор равен нулю или нет. А это свойство минора не изменится при умножении строки или столбца на число, отличное от нуля. Если утверждение справедливо для второго преобразования, то его справедливость для третьего вытекает из доказанной леммы.
Доказательство проведем для строк матрицы А (для столбцов оно будет аналогичным). Обозначим 


Пусть 

1. Покажем, что матрица 
А) Матрица А имеет отличный от нуля минор R-го порядка, не содержащий I — й строки. Этот же минор является и минором матрицы 
Б) Все миноры R-го порядка матрицы А, не содержащие I — й строки, равны нулю. Пусть 



(волна указывает, что эти строки короче, они содержат только те элементы, которые принадлежат выделенным столбцам). В равенстве (1) определитель 



2. Покажем, что все миноры (R+1)-го порядка матрицы 
А) Минор (R+1)-го порядка матрицы 
Б) Минор 


В равенстве (2) 




Свойства ранга матрицы
1°. Ранг матрицы не превосходит ни количества ее строк, ни количества столбцов.
2°. При транспонировании матрицы ее ранг не меняется.
3°. Если rang A = 0, то A – нулевая матрица.
4°. Если у матрицы вычеркнуть столбец или строку, полностью состоящую из нулей, то ее ранг при этом не изменится.
5°. Если у матрицы вычеркнуть однy из двух пропорциональных строк (столбцов), то её ранг при этом не изменится.
6°. Ранг произведения матриц не превосходит ранга каждого из сомножителей. При этом, если один из сомножителей – невырожденная матрица, то ранг произведения равен рангу второго сомножителя.
Первые четыре свойства очевидны, пятое вытекает из доказанной теоремы, а шестое мы докажем позже, в четвёртой главе.
§ 3. Теорема о базисном миноре
Определение. Строки матрицы А

Называются Линейно зависимыми, если существуют числа 

Строки (1) называются Линейно независимыми, если равенство (2) выполняется Только в том случае, когда 
Аналогично формулируется определение линейной зависимости и независимости для столбцов матрицы (позднее мы введем понятия линейной зависимости и независимости в более общем случае).
Определение. Базисным минором матрицы называется любой отличный от нуля её минор, порядок которого равен рангу этой матрицы. Строки (столбцы), проходящие через базисный минор, называются Базисными.
Теорема 1 (о базисном миноре). Справедливы следующие утверждения:
1. Базисные строки (столбцы) матрицы линейно независимы.
2. Каждая из небазисных строк (столбцов) может быть представлена в виде линейной комбинации базисных.
►Пусть 

Обозначим М её базисный минор, М≠0. Приступаем непосредственно к доказательству.
1. Для доказательства линейной независимости строк

Составляем их линейную комбинацию и приравниваем её нулевой строке:

Матрицы равны в том и только в том случае, когда равны их соответствующие элементы. Приравнивая нулю первые R Элементов матрицы-строки из левой части равенства (4), получаем следующую систему:

Конечно, мы могли бы приравнять нулю и все остальные элементы матрицы, но в этом, как вы увидите, нет никакой необходимости.
Система (5) — система линейных уравнений относительно 

2. Нужно доказать, что 




К базисным строкам и столбцам добавим одну из небазисных строк и произвольный столбец и рассмотрим полученный определитель:

Определитель 






Так как 


При вычислении алгебраических дополнений к элементам последнего столбца дописанный J-й столбец вычеркивается, значит, алгебраические дополнения 

Теорема 2 (О линейной независимости строк и столбцов). Для того чтобы строки (столбцы) матрицы были линейно независимы необходимо и достаточно, чтобы ее ранг равнялся количеству строк (столбцов).
►Доказательство проводим для строк матрицы (для столбцов оно будет аналогичным).
Необходимость. Дано: строки матрицы линейно независимы. Пусть 


Среди чисел (9) есть отличные от нуля, и

Таким образом, строки матрицы линейно зависимы, и мы пришли к противоречию. Следовательно, предположение неверно и 
Достаточность. Дано: 
1. Для того чтобы строки (столбцы) матрицы были линейно зависимы, необходимо и достаточно, чтобы ее ранг был меньше количества строк (столбцов).
2. Для того чтобы строки (столбцы) определителя были линейно независимы необходимо и достаточно, чтобы он был отличен от 0.
► <строки 

3. Для того чтобы строки (столбцы) определителя были линейно зависимы необходимо и достаточно, чтобы он был равен 0.
§ 4. Критерий совместности линейных уравнений
Теорема Кронекера – Капелли (Критерий совместности системы линейных Уравнений). Для того чтобы система линейных уравнений была совместной необходимо и достаточно, чтобы ранг матрицы системы равнялся рангу расширенной матрицы (
►Пусть задана система линейных уравнений

С матрицей А. Будем обозначать 

Необходимость. Дано: система совместна. Следовательно, существует упорядоченный набор чисел 
Получаем: 

Достаточность. Дано: 



§ 5. Однородные системы линейных уравнений
Определение. Система линейных уравнений называется Однородной, если во всех ее уравнениях свободные члены равны нулю:

Часто удобно использовать и матричную запись:
Однородная система всегда совместна, она имеет, по крайней мере, решение 



Рассмотрим различные случаи.
1. Если 
2. Пусть 


Она имеет единственное решение 

Решение системы (3) и исходной системы. Так как свободным неизвестным можно придать значения бесконечным числом способов, то при условии 
Вывод. Для того чтобы однородная система линейных уравнений имела нетривиальные решения, необходимо и достаточно, чтобы ранг ее матрицы был меньше количества неизвестных. В частности, если в однородной системе число уравнений равно числу неизвестных, то для существования нетривиальных решений необходимо и достаточно, чтобы определитель матрицы системы был равен нулю.
Свойства решений однородной системы линейных уравнений
1°. Сумма решений однородной системы также является ее решением.
►<X1, X2 – решения (2)> 

2°. Если решение однородной системы умножить на число, то также получим ее решение.
►<Х – решение (2)>

3°. При условии 


►Построим систему решений следующим образом: для решения 






(звездочками здесь отмечены значения неизвестных, которые для наших рассуждений не так уж и важны). Так как 
4°. Каждое решение однородной системы может быть представлено в виде линейной комбинации решений её фундаментальной системы
►Обозначим X0 произвольное решение однородной системы,
И построим вспомогательный столбец

Из свойств 1° и 2° вытекает, что 





Которая имеет единственное тривиальное решение 


Замечания. 1. При доказательстве свойства 3° мы получили следующее правило: для построения фундаментальной системы решений следует свободным неизвестным придать значения по строкам единичной (или любой невырожденной) матрицы и найти соответствующие значения базисных неизвестных, решая систему (4). На практике сначала решают систему (4) в общем виде, выражая все неизвестные через свободные, а затем придают им необходимые значения.
2. Из доказанных свойств вытекает, что множество всех решений однородной системы линейных уравнений совпадает с множеством всевозможных линейных комбинаций решений её фундаментальной системы (т. е. решений вида (6)).
Определение. Множество всех решений системы линейных уравнений, выраженное через параметры (свободные неизвестные), называется Общим решением системы линейных уравнений. Каждое решение системы называется её Частным решением.
Чтобы получить какое-либо частное решение, следует в общем решении придать свободным неизвестным какие-то конкретные значения
§ 6. Неоднородные системы линейных уравнений
Пусть задана неоднородная система линейных уравнений
В матричной записи. Наряду с (1) рассмотрим однородную систему
С той же матрицей, что и система (1). Однородную систему (2) будем называть союзной для неоднородной системы (1).
Теорема. Справедливы следующие утверждения:
1. Разность решений неоднородной системы линейных уравнений является решением союзной к ней однородной системы.
2. Сумма решения неоднородной системы линейных уравнений и решения союзной к ней однородной является решением неоднородной системы.
3. Если неоднородная система линейных уравнений имеет решение 

Где 
►1. 

2. <



3. Пусть система (1) имеет некоторое решение 




Итак, если неоднородная система линейных уравнений имеет решение 
Вывод. Пусть 



§7. Метод Гаусса решения системы линейных уравнений
Теорема. С помощью элементарных преобразований только над строками и перестановки столбцов любая ненулевая матрица может быть приведена к простейшему виду, т. е. к виду, когда в её левом верхнем углу находится единичная матрица, а последние строки полностью состоят из нулей.
►Пусть задана ненулевая матрица
(верхний индекс будет обозначать номер шага). Предположим, например, что 


Которую, в свою очередь, преобразуем так: к I — й строке прибавим первую, умноженную на 


Где 

Выберем теперь среди чисел 


Строки которой, в том числе и первую, преобразуем так: к I-й строке прибавляем вторую, умноженную на 

Теперь выбираем отличный от нуля элемент в последних (
Замечание. На самом деле перестановкой столбцов мы заниматься не будем. Базисный минор вовсе не обязательно перемещать в первые столбцы и приводить к виду единичной матрицы, достаточно, чтобы в каждом из его столбцов был единственный отличный от нуля элемент. Кроме того, чтобы избежать дробей, строчки также не будем делить на опорный элемент. При переходе от каждой матрицы к следующей поступаем так:
А) выбираем опорный элемент 
Б) опорную строку оставляем без изменений, опорный столбец дополняем нулями;
В) предыдущие опорные столбцы умножаем на новый опорный элемент;
Г) остальные элементы пересчитываем по правилу прямоугольника:

Правило решения системы линейных уравнений
1. Вычисляем одновременно ранг матрицы системы и ранг расширенной матрицы, приводя матрицу А с помощью элементарных преобразований строк матрицы 

2. Если 
3. Если 



Её базисный минор расположен в первых 

Пример. Решим методом Гаусса систему линейных уравнений
▼Составляем расширенную матрицу и приводим её к простейшему виду методом опорного элемента. При этом всякий раз получаем матрицу системы, равносильной исходной. Поэтому между матрицами можно ставить знак равносильности. Опорный элемент будем подчеркивать двойной чертой.

Базисный минор можно выбрать, например, в первом, третьем и четвертом столбцах. Тогда базисными будут неизвестные 


Общее решение выглядит так:

§ 8. Еще раз об обратной матрице
Если квадратная матрица 
Пусть 


Обозначим 






<(1)> 





Таким образом, матричное уравнение (1) равносильно системе

Состоящей из систем линейных уравнений с одной и той же невырожденной матрицей 



<




Тогда 
Так как в (2) все системы имеют одну и туже матрицу, то нет необходимости преобразовывать отдельно расширенную матрицу каждой из этих систем, а можно это сделать вместе, записав матрицу 


Из вышесказанного вытекает правило нахождения обратной матрицы: записываем расширенную матрицу 




Пример. С помощью элементарных преобразований найдем обратную для матрицы









Глава 2 МЕТОДЫ РЕШЕНИЯ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
Описание презентации по отдельным слайдам:
Глава 2
МЕТОДЫ РЕШЕНИЯ СИСТЕМ
ЛИНЕЙНЫХ УРАВНЕНИЙ
2.1. Общая характеристика методов решения
систем линейных уравнений
2.2. Метод обратной матрицы. Формула Крамера
Имеем линейную систему уравнений с n неизвестными:
.
…
(2.1)
Введем матрицы:
– матрица системы из
коэффициентов при неизвестных,
– вектор-столбец неизвестных,
– вектор-столбец свободных членов.
Системе (2.1) соответствует матричное уравнение
. (2.2)
Решение уравнения (2.2) на базе обратной матрицы
имеет вид
. (2.3)
Другой разновидностью формы решения (2.3)
является формула Крамера
, (2.5)
,
где Δ – главный определитель системы (2.1);
– номера столбцов;
– определитель, полученный
путем замены в главном
определителе системы (Δ)
столбца коэффициентов при
неизвестном xj столбцом
коэффициентов свободных
членов (B).
2.3. Метод Гаусса
Для простоты рассуждений ограничимся
рассмотрением системы четырех уравнений с четырьмя
неизвестными
1)
2)
3)
4)
(2.7)
,
,
,
.
Изложим последовательность операций
при прямом ходе.
Первый шаг. Разделим коэффициенты первого
уравнения на a11, в результате чего оно примет вид
.
(2.8)
Пользуясь уравнением (2.8), можно исключить
Переменную x1 из уравнений № 2, 3, 4 системы (2.7).
Для этого нужно из уравнения №2 системы вычесть
уравнение (2.8), умноженное на a21, из уравнения №3 системы вычесть уравнения (2.8), умноженное на a31 и
т.д. В результате получим систему из трех уравнений с тремя неизвестными:
1)
2)
3)
(2.9)
,
,
.
Второй шаг состоит в исключении x2 из уравнений
№ 2, 3 системы (2.9).
(2.11)
.
Используя (2.11), исключаем x2 из уравнений № 2, 3
системы (2.9) и получаем систему второго порядка:
1)
2)
(2.12)
,
.
Третий шаг. Разделим первое уравнение
системы (2.12) на ведущий элемент , что дает
(2.13)
.
С помощью этого уравнения исключим x3 из второго
уравнения системы (2.12) и получим
(2.14)
.
Таким образом, исходную систему (2.7) удалось
привести к эквивалентной системе с треугольной
матрицей:
(2.15)
.
,
,
,
Обратный ход связан с последовательным
переходом от последнего уравнения системы (2.15)
к первому, в процессе которого осуществляется
непосредственный расчет значений x:
(2.16)
.
,
,
,
(2.21)
.
Определитель матрицы A равен произведению
«ведущих» элементов в схеме Гаусса:
(2.22)
.
2.4. Метод простой итерации
для решения систем линейных уравнений
Имеем линейную систему уравнений с n неизвестными:
.
…
(2.23)
,
,
Итерационный процесс для системы (2.24):
(2.27)
где k – номер итерации.
Для сходящегося процесса решением является
,
.
(2.28)
Условие сходимости:
(2.39)
,
т.е. модуль диагонального коэффициента для каждого
уравнения больше суммы модулей его недиагональных
коэффициентов.
Условие завершения итерационного процесса:
.
(2.44)
2.5. Метод Зейделя для решения линейных систем
Метод Зейделя представляет собой некоторую
модификацию метода простой итерации.
Считаем, что дана линейная система, приведенная
к итерационному виду (2.24):
.
(2.62)
Полагаем, что найдено k-е приближение
всех корней. Согласно методу Зейделя, (k+1)-е
приближение корней будет определяться по следующим
формулам:
,
,
,
…
,
…
,
.
(2.63)
Метод Зейделя обеспечивает, как правило, лучшую
сходимость, чем метод простой итерации.
Курс повышения квалификации
Охрана труда
- Сейчас обучается 120 человек из 44 регионов
Курс профессиональной переподготовки
Охрана труда
- Сейчас обучается 236 человек из 54 регионов
Курс профессиональной переподготовки
Библиотечно-библиографические и информационные знания в педагогическом процессе
- Сейчас обучается 353 человека из 64 регионов
Ищем педагогов в команду «Инфоурок»
Дистанционные курсы для педагогов
«Взбодрись! Нейрогимнастика для успешной учёбы и комфортной жизни»
Свидетельство и скидка на обучение каждому участнику
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
5 594 359 материалов в базе
Самые массовые международные дистанционные
Школьные Инфоконкурсы 2022
33 конкурса для учеников 1–11 классов и дошкольников от проекта «Инфоурок»
«Психологические методы развития навыков эффективного общения и чтения на английском языке у младших школьников»
Свидетельство и скидка на обучение каждому участнику
Другие материалы
- 04.12.2020
- 94
- 1
- 06.10.2020
- 142
- 0
- 02.10.2020
- 91
- 0
- 01.10.2020
- 140
- 0
- 01.10.2020
- 117
- 0
- 23.09.2020
- 73
- 0
- 20.09.2020
- 75
- 0
- 26.08.2020
- 82
- 0
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Добавить в избранное
- 10.11.2020 92
- PPTX 175 кбайт
- 2 скачивания
- Оцените материал:
Настоящий материал опубликован пользователем Данилова Екатерина Николаевна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт
Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.
Автор материала
- На сайте: 1 год и 2 месяца
- Подписчики: 0
- Всего просмотров: 33301
- Всего материалов: 232
Московский институт профессиональной
переподготовки и повышения
квалификации педагогов
Дистанционные курсы
для педагогов
663 курса от 690 рублей
Выбрать курс со скидкой
Выдаём документы
установленного образца!
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
В Белгородской области отменяют занятия в школах и детсадах на границе с Украиной
Время чтения: 0 минут
Новые курсы: функциональная грамотность, ФГОС НОО, инклюзивное обучение и другие
Время чтения: 15 минут
Минобрнауки и Минпросвещения запустили горячие линии по оказанию психологической помощи
Время чтения: 1 минута
Школьник из Сочи выиграл международный турнир по шахматам в Сербии
Время чтения: 1 минута
Минпросвещения России подготовит учителей для обучения детей из Донбасса
Время чтения: 1 минута
Школы смогут вносить данные в портфолио школьника в «МЭШ»
Время чтения: 2 минуты
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
Глава 2. Системы линейных алгебраических уравнений (СЛАУ)
2.1. Основные понятия и определения.
В общем случае система n линейных с неизвестными уравнений имеет вид:
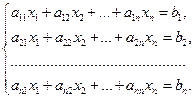
Через 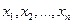
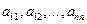
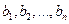
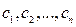
Условие совместимости СЛАУ. Теорема Кронекера-Капелли
Рассмотрим систему (10). Матрицей этой системы будем называть матрицу, составленную из ее коэффициентов: 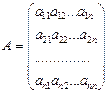
Если к этой матрице добавить столбец свободных членов, получим расширенную матрицу:
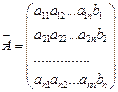
Теорема Кронекера–Капелли. Система линейных уравнений совместна тогда и только тогда, когда ранг расширенной матрицы равен рангу матрицы системы.
Доказательство. Необходимость. Предположим, что система совместна, тогда имеется решение этой системы 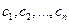
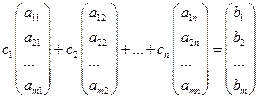
Последний столбец расширенной матрицы является линейной комбинацией её остальных столбцов, поэтому ранг расширенной матрицы будет равен рангу системы.
Достаточность. Предположим, что ранг расширенной матрицы равен рангу системы и равен числу r: 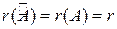
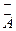
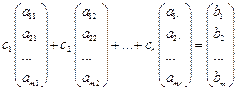
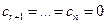
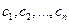
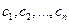
Правило Крамера решения СЛАУ
Рассмотрим систему n линейных уравнений с n неизвестными (2.1). Введем матрицу неизвестных Х: 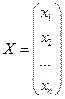
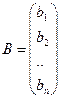
Считаем, что определитель матрицы системы (2.1) 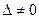
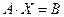
Поскольку определитель системы отличен от нуля, матрица А имеет обратную матрицу А –1 . Для доказательства существования решения воспользуемся теоремой Кронекера–Капели. Ранг матрицы системы равен n, а ранг расширенной матрицы, содержащей n строк, больше числа n быть не может. Умножим матричное уравнение слева на обратную матрицу А –1 : 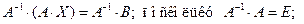
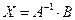
Используя формулу для обратной матрицы и введя обозначения: 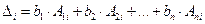
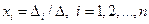
Определитель 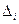
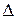
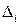
Например, для системы трех линейных уравнений с тремя неизвестными: если определитель системы 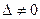
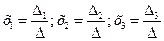
Пример 2.1. Решить систему
Необходимо вычислить четыре определителя по формулам Крамера:
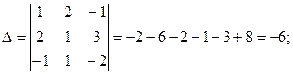
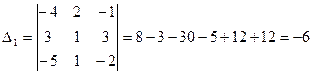
Тогда 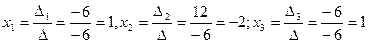
Проверкой убеждаемся в правильности вычислений.
Метод Гаусса
Рассмотрим систему n линейных уравнений с n неизвестными (2.1). Метод Гаусса представляет собой систематизированную схему последовательного исключения неизвестных. Пусть 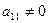
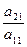
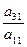
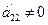
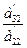
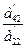
Эта процедура называется прямым ходом метода Гаусса. Далее начинаем обратный ход метода Гаусса, т.е. нахождение неизвестных. Находим xn из последнего уравнения, затем найденное значение xn подставляем в предпоследнее уравнение и определяем xn–1. Найденные значения xn и xn–1подставляем в (n – 2)-е уравнение и находим хn–2. Продолжая этот процесс, определяем остальные неизвестные системы.
Мы полагали, что 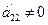
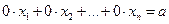
Если а=0, то система имеет бесконечное количество решений. При этом одно (или несколько) уравнений являются следствием остальных.
Если 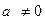
Как отыскивать решения системы в первом случае, будет указано в следующем пункте. При решении систем линейных уравнений методом Гаусса удобно приводить к треугольному (или ступенчатому) виду не саму систему уравнений, а расширенную матрицу этой системы, выполняя все преобразования над ее строками. Последовательно получающиеся в ходе преобразования матрицы обычно соединяют знаком эквивалентности.
Пример 2.2. Решить систему из примера 2.1 методом Гаусса. Запишем расширенную матрицу системы:
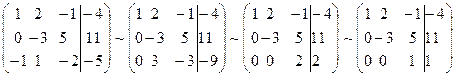
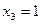
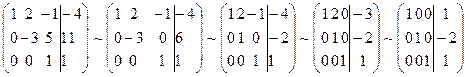
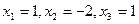
Решение произвольных СЛАУ
Рассмотрим систему m линейных уравнений с n неизвестными:
Для решения произвольной системы алгебраических уравнений необходимо вычислить ранг матрицы системы r(А). Если он совпадает с рангом расширенной матрицы, то система имеет решение. Считаем, что базисный минор расположен в первых r строках и столбцах системы. Уравнения, соответствующие базисным строкам, назовем базисными уравнениями. Неизвестные, соответствующие базисным столбцам, назовем главными, а остальные – свободными. Система линейных уравнений эквивалентна системе своих базисных уравнений.
Если r = n, то система имеет единственное решение по теореме Кронекера–Капели. Если r
Последнее изменение этой страницы: 2017-03-14; Просмотров: 316; Нарушение авторского права страницы
http://infourok.ru/glava-2-metody-resheniya-sistem-linejnyh-uravnenij-4833823.html
http://lektsia.com/7x3e63.html