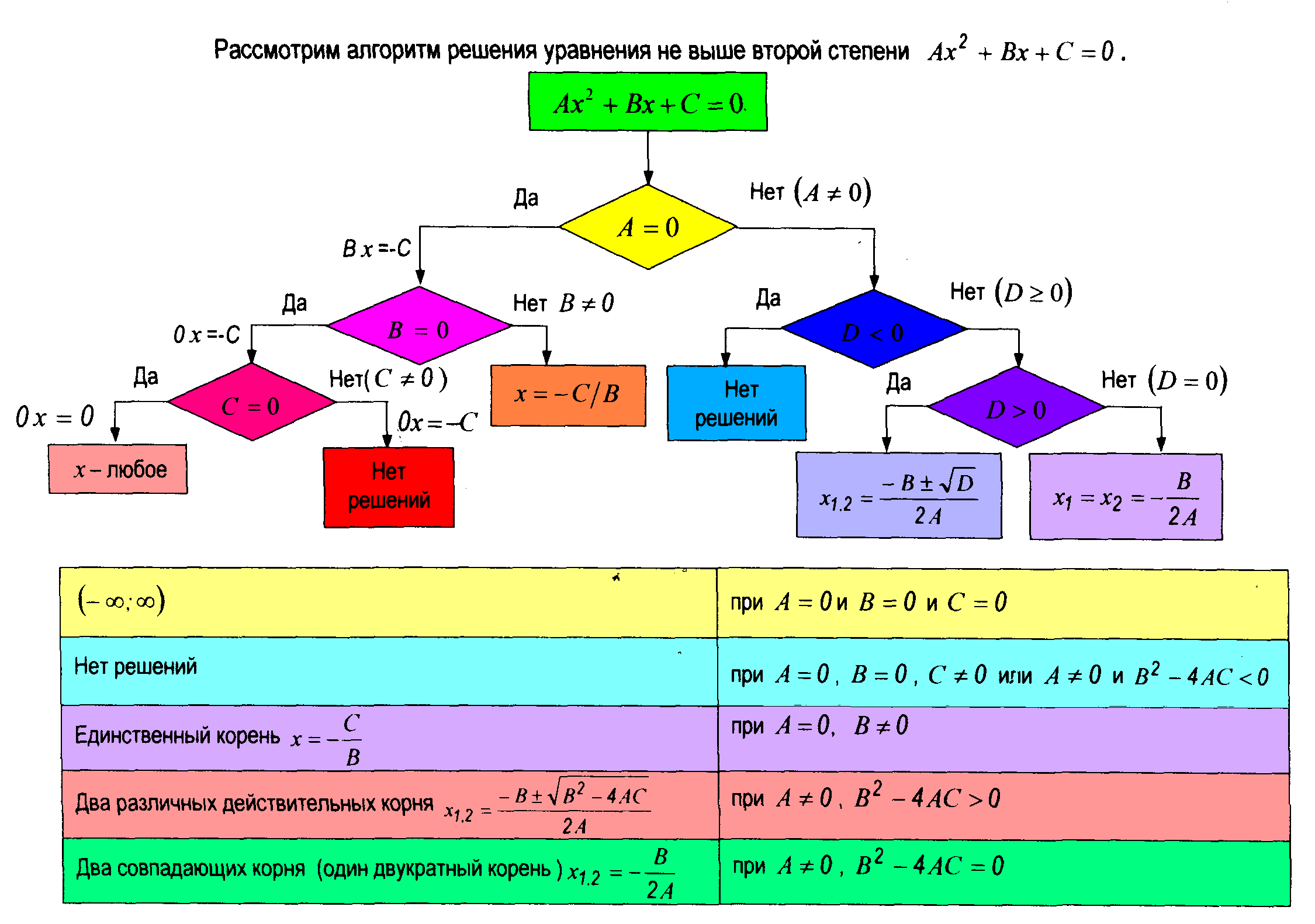
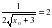Исследовательская работа по математике «Аналитический и графический методы решения уравнений с параметрами»
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
Министерство Образования и науки Республики Дагестан
Семнадцатая Республиканская научная конференция молодых исследователей
Аналитический и графический методы решения
уравнений с параметрами
Сотавов Артур Русланович,
ученик 11 «а» класса
Гимназии им. М. Горького
Заря Оксана Владимировна
Гимназии им. М. Горького
Хасавюрт, 2011 г.
1. Приобрести навык решения уравнений с параметрами различных видов;
2. Рассмотреть два метода решения уравнений с параметрами: аналитический и графический;
3. Использовать приобретенные умения и навыки при решении заданий с параметрами на ЕГЭ.
1. Использование эвристических приемов общего характера, применяемых в исследованиях математического материала;
2. Применение основных разделов школьной математики;
3. Решение аналитическим и графическим способами уравнений с параметрами – отдельная составляющая школьного курса математики.
1. Формирование логического мышления и математической культуры;
2. Выбор наиболее рациональных способ решений уравнений с параметрами, применяя аналитический и графический метод решения уравнений с параметрами;
3. Путем исследования способов решения уравнений с параметром показать, что с научной точки зрения, владение приемами решения задач с параметрами — критерий знаний основного раздела школьной математики.
Знакомство с понятием «параметр»………………………………………………………….2
Аналитический метод решения уравнений с параметрами…………………………………3
2.1. Решение уравнений первой степени с одним неизвестным………………………. 4
2.3. Дробно-рациональные уравнения……………………………………………………..5
2.4. Иррациональные уравнения, содержащие параметр…………………………………6
2.5. Элементы математического анализа…………………………………………………..7
Графический метод решения уравнений с параметрами……………………………………7
Изучение многих физических процессов и геометрических закономерностей часто приводит к решению уравнений, содержащих параметр. Способы решения задач с параметрами не изучаются как отдельная составляющая школьного курса математики, и рассматриваются только на немногочисленных факультативных занятиях.
В настоящее время различные задачи с параметрами – это одни из самых сложных заданий на экзамене по математике. Среди заданий группы «С» одно – задача с параметрами. Таким образом, получение отличной отметки при различных формах проведения экзамена по математике без решения задач с параметрами становится неразрешимой проблемой. Многие даже не берутся решать эти задания, так как заведомо считают, что не смогут их решить, даже не попробовав.
При решении примеров с параметрами применяются: аналитический способ; метод координат (система координат на прямой и на плоскости); метод сечений; нестандартные и логические задачи.
В данной работе будут рассмотрены аналитический способ и метод координат.
Применение разработанной на основе общих методов решения уравнений, содержащих параметры, методики их решения позволит решать уравнения, содержащие параметры, на сознательной основе, выбирать наиболее рациональный метод решения, применять разные методы решения.
В своей работе я исследовал формы решения задач с параметрами, так как именно они вызывают у большинства наибольшие затруднения. Мне самому нужно будет сдавать ЕГЭ, и поэтому, обращаясь к этой теме, хочу предложить свою работу в качестве методического пособия.
Глава I . ЗНАКОМСВО С ПОНЯТИЕМ «ПАРАМЕТР».

с неизвестными х, у, . z и с параметрами 

с неизвестными х, у. z, не содержащих параметров. Уравнение (F0) имеет некоторое вполне определенное множество (быть, может, пустое) решений.
Аналогично рассматриваются неравенства и системы, содержащие параметры. Допустимыми системами значений параметров считаются системы, допустимые для каждого уравнения в отдельности.
Определение. Решить уравнение, содержащее параметры, это значит, для каждой допустимой системы значений параметров найти множество всех решений данного уравнения.
Понятие эквивалентности применительно к уравнениям, содержащие параметр, устанавливается следующим образом.
Определение. Два уравнения F(х, у, . z; 
Ф (х, у, . z; 
с неизвестным х, у. z и с параметрами 
Итак, эквивалентные уравнения при всякой допустимой системе значений параметров имеют одно и то же множество решений.
Преобразование уравнения, изменяющее множество допустимых систем значений параметров, приводит к уравнению, не эквивалентному данному уравнению.
Предположим, что каждое из неизвестных, содержащихся в уравнении
F ( x , у, z; 
задано в виде некоторой функции от параметров:
х = х( 


Говорят, что система функций (Х), заданных совместно, удовлетворяет уравнению (F), если при подстановке этих функций вместо неизвестных х, у. z в уравнение (F) левая его часть обращается в нуль тождественно при всех допустимых значениях параметров:
F ( x ( 


Глава II . Аналитический метод решения уравнений с параметрами
Задачи с параметрами играют важную роль в формировании логического мышления и математической культуры у школьников, но их решение вызывает у них значительные затруднения. Это связано с тем, что каждое уравнение с параметрами представляет собой целый класс обычных уравнений, для каждого из которых должно быть получено решение. Такие задачи предлагаются на едином государственном экзамене и на вступительных экзаменах в вузы.
Основное, что нужно усвоить при первом знакомстве с параметром, — это необходимость осторожного, даже, если хотите, деликатного обращения с фиксированным, но неизвестным числом.
При одних значениях параметров уравнение не имеет корней, при других – имеет только один корень, при третьих – два корня.
При решении таких уравнений надо:
1) найти множество всех доступных значений параметров;
2) перенести все члены, содержащие неизвестное, в левую часть уравнения, а все члены, не содержащие неизвестного в правую;
3) привести подобные слагаемые;
4) решать уравнение ax = b .
Возможно три случая.
1. а 
х = 
2. а = 0, b = 0. Уравнение принимает вид: 0х = 0, решениями являются все х 
3. а = 0, b ≠ 0. Уравнение 0х = b решений не имеет.
Сделаем одно замечание. Существенным этапом решения уравнений с параметрами является запись ответа. Особенно это относится к тем примерам, где решение как бы «ветвится» в зависимости от значений параметра. В подобных случаях составление ответа – это сбор ранее полученных результатов. И здесь очень важно не забыть отразить в ответе все этапы решения.
В только что разобранном примере запись ответа практически повторяет решение. Тем не менее, я считаю целесообразным привести ответ.
Ответ: х = 

х – любое число при а = 0, b = 0; решений нет при а = 0, b ≠ 0.
Многие учащиеся принимают параметр как какое-то одно число, тогда как, хотя он и является фиксированным числом, но может принимать любое действительное значение. Поэтому при решении задач с параметром следует соблюдать особую осторожность, чтобы не попасть впросак.
2.1. Решение уравнений первой степени с одним неизвестным.
Пример 1: Решите при всех значениях параметра а уравнение
Решение: Необходимо решить линейное уравнение с параметром. Сначала перенесем все неизвестные слагаемые в левую часть уравнения и приведем подобные слагаемые. Получим (а-2)х=5.
Чтобы найти значение х, в данном случае надо разделить уравнение на (а-2). При всех ли значениях параметра а мы можем уравнение разделить на (а-2)? Нет.
При а=2 выражение а-2 обращается в нуль, поэтому значение параметра а=2 является «особым» — контрольным значением параметра. Рассмотрим это значение отдельно.
При а=2; (2-2)х=5; 0х=5 – уравнение решений не имеет.
Теперь а≠2, и, чтобы выразить х, делим обе части уравнения на (а-2).
При а≠2 получим 
Ответ: при а=2 решений нет; при а≠2 
Пример 2: При каких значениях параметра уравнение ( b -1) x 2 +( b +4) x + b +7=0 имеет только один корень?
Решение: При всех ли значениях параметра данное уравнение будет квадратным? Нет.
При b =1 уравнение становится линейным ( b =1 – контрольное значение параметра). Подставим значение b =1 в исходное уравнение:
(1-1)х 2 +(1+4)х+1+7=0,5х+8=0. Это уравнение имеет один корень -1,6.
При b 
Находим дискриминант и приравниваем его к нулю.
D=(b+4) 2 -4∙(b-1)(b+7)=b 2 +8b+16-4(b 2 +6b-7)=-3b 2 -16b+44=0
Ответ: при b =1 ; b =2; b =-22/3 уравнение имеет только один корень.
Процесс решения дробно-рациональных уравнений протекает по обычной схеме: данное уравнение заменяется целым путем умножения обеих частей уравнения на общий знаменатель левой и правой его частей. После чего учащиеся решают известным им способом целое уравнение, исключая посторонние корни, то есть числа, которые обращают общий знаменатель в нуль. В случае уравнений с параметрами эта задача более сложная. Здесь, чтобы посторонние корни исключить, требуется находить значение параметра, обращающее общий знаменатель в нуль, то есть решать соответствующие уравнения относительно параметра .
Пример 3 : Решить уравнение

Решение . Значение а=0 является контрольным. При a=0 уравнение (1) теряет смысл и, следовательно, не имеет корней. Если а≠0, то после преобразований уравнение (4) примет вид: х 2 +2 (1 — а) х +а 2 — 2а — 3=0. (2)
Найдем дискриминант уравнения (2) 
Таким образом, при а = — 2 х1—посторонний корень уравнения (1).
Таким образом, при а = — 3 x1— посторонний корень уравнения (1).
Таким образом, при а=2 х2 — посторонний корень уравнения (1).
Таким образом, при а = 1 х2— посторонний корень уравнения (1)
При а = — 3 получаем х= — 6; при a = — 2 х = — 5;
При a=1 х = 1+1=2; при a=2 х=2+1=3. Итак, можно записать
Ответ : 1) если a = — 3, то х = — 6; 2) если a = -2, то х = — 5; 3) если a = 0, то корней нет; 4) если a = 1, то х=2; 5) если а = 2, то х = 3; 6) если 
2.4. Иррациональные уравнения, содержащие параметр
Главными особенностями при решении уравнений такого типа являются:
1. ограничение области определения неизвестной х, так как она меняется в зависимости от значения параметра.
2. в решении уравнений вида 

При рассмотрении всех особых случаев и возведении обеих частей иррационального уравнения в квадрат мы переходим к решению квадратного уравнения с параметром.
Рассмотрим несколько примеров и попробуем заметить эти особенности при решении.
Пример 4: В зависимости от значения параметра 

Итак, мы вплотную подошли к задаче рассмотрения различных случаев параметра
Если 
Если 




Ответ : При 

2.5. Элементы математического анализа
Пример 5: Найти все такие значения параметра, что наименьшее значение функции 
Решение: Наименьшее значение 


Ответ: a 

Глава III . Графический метод решения уравнений с параметрами
В практике вступительных экзаменов в вариантах ЕГЭ можно выделить задачи на исследование уравнения или неравенства 

В средней школе учащиеся знакомятся с графической иллюстрацией уравнения или неравенства вида 


В общем случае, когда построение графика функции 

Графическое представление уравнения с параметром обладает несколькими несомненными преимуществами:
1. построив график (графики), можно определить, как влияет на них и, соответственно, на решение уравнения изменение параметра;
2. иногда график дает возможность сформулировать аналитически необходимые и достаточные условия для решения поставленной задачи;
3. ряд теорем позволяет на основании графической информации делать вполне строгие и обоснованные заключения о решениях уравнения, об их границах и т.д.
В случаях, когда результат, полученный с помощью графического метода, вызывает сомнения, его необходимо подкрепить аналитически.
Пример 6: Решить уравнение 
Решение: Уравнения с модулем можно решать графически. Для этого выражения, содержащие параметр, переносят в одну часть уравнения и строят графики функций левой и правых частей уравнения. 
Будем строить в одной системе координат графики функций 

1) При а>1 графики выглядят следующим образом (см. прил. 1). Графики
пересекаются в одной точке: (1;0), т.е. при а>1 х=1
2) При а=1 графики выглядят следующим образом (см. прил. 2). При 
совпадают, т.е. система имеет бесконечно много решений. При а=1 решением будет промежуток [1;+∞).
3) При 0 a графики выглядят следующим образом (см. прил. 3). Графики
пересекаются в двух точках. Одна точка имеет координаты (1;0). Чтобы найти координаты второй точки, надо решить систему
Так как x , то модули выражений раскрываются следующим образом:


4) При а=0 график 
Ответ: при a >1 x =1 ; при a =1 x ≥1 ; при 0 a x =1 и 
Пример 7: Решить систему уравнений 
Будем строить в одной системе координат графики функц ий 


1) 
О1(5;4), R 1 =2; О2(2;0), R 2 = 



2) 
О1(-5;4), R 1 =2; О2(2;0), R 2 = 



Ответ: при 

C научной точки зрения, владение приемами решения задач с параметрам можно считать критерием знаний основных разделов школьной математики, уровня математического и логического мышления.
Решение задач, уравнений с параметрами, открыло значительное число эвристических приемов общего характера, ценных для математического развития личности, применяемых в исследованиях и на любом другом
математическом материале. Именно такие задачи развивают логическое мышление и математическую культуру. Владение методами решения задач с параметрами помогли мне успешно справиться с другими задачами.
В моей работе я рассмотрел следующие виды заданий с параметрами:
1) решение уравнений первой степени с одним неизвестным;
2) решение квадратных уравнений;
3) решение дробно-рациональных уравнений;
4) решение иррациональных уравнений;
5) решение уравнений, использовав элементы мат. анализа;
6) решение уравнений, содержащих модуль.
При исследовании способов решения уравнения с параметрами я столкнулся с определенными трудностями, связанными со следующими особенностями:
— обилие формул и методов, используемых при решении уравнений данного вида;
— возможность решения одного и того же уравнения, содержащего параметр различными методами.
Конечно, не все далось сразу и легко – чтобы научиться решать уравнения с параметрами, нужно выйти за рамки представлений об уравнении, при этом не забывая о свойствах того или иного типа уравнения. Удалось это не сразу. К тому же, в школьной программе задачам с параметрами не уделяется должного внимания, поэтому, не изучив данные способы, можно растеряться.
Исследовав способы решения уравнений с параметрами я действительно понял, как решаются уравнения с параметрами, приобрел навык решения и, надеюсь, теперь не столкнусь с трудностями при решении подобных заданий на ЕГЭ.
5. В.В. Кочагин, М.И. Кочагина Интенсивная подготовка к ЕГЭ(математика) – Москва, 2010г.
6. Э.И.Эфендиев Практикум по элементарной математике – Махачкала, 2004г.
7. М.И. Шабунин Уравнения и системы уравнений с параметром /Математика в школе №3, 2003г./
8. А.Г.Корянов, А.А. Прокофьев Использование метода наглядной графической интерпретации при решении уравнений и неравенств с параметрами (начало) /Математика в школе №1,2011г/;
9. А.Г.Корянов, А.А. Прокофьев Использование метода наглядной графической интерпретации при решении уравнений и неравенств с параметрами (окончание) /Математика в школе №2, 2011г/;
10. В.И.Горбачев Общие методы решения уравнений и неравенств с параметрами не выше второй степени /Математика в школе №2, 2000г/
Занятие элективного курса: «Различные способы решения уравнений с параметром: аналитическим и графическим методом».
Задания с параметрами традиционно считаются одними из самых сложных в школьном курсе математики.Однако в тестах по ЕГЭ и ОГЭ они обязательно присутствуют. Поэтому умение их решать- залог успеха на экзамене. Данное занятие как раз помогает школьникам научиться решатьподобные задания. Материал урока направлен на развитие логического мышления, алгоритмической культуры, интуиции, навыков исследовательской деятельности, творческих способностей ущащихся.
Просмотр содержимого документа
«Занятие элективного курса: «Различные способы решения уравнений с параметром: аналитическим и графическим методом». »
Соловьева Екатерина Николаевна
Класс: 9. Дата проведения: 21.01.15.
Тема: Различные способы решения уравнений с параметром: аналитическим и графическим методом.
Тип урока: урок повторения.
Цель: — способствовать формированию умений решать уравнения с параметром;
— способствовать развитию навыков исследовательской деятельности;
— способствовать развитию навыков самоконтроля;
— способствовать развитию поисковой и познавательной активности.
Средства: опорные схемы, мультимедиа, доска, мел.
Рассмотрение способов решения
Постановка домашнего задания и рефлексия
Здравствуйте. Тема нашего сегодняшнего урока: Решение уравнений с параметром графическим методом.
Давайте вспомним: Какое уравнение называется уравнением с параметром? (Уравнениями с параметром называются уравнения, у которых коэффициенты заданы не конкретными числовыми значениями, а обозначены буквами.)
Что значит аналитически решить уравнение? (Это решение, представленное в виде формулы (и соответственно полученное тоже путем математических выкладок).)
Что значит графически решить уравнение? (Построить график левой части и график правой части. Абсцисса точки пересечения и будет решением.)
Употребление букв и разных других математических знаков появилось не сразу, а в результате долгого развития математики. Оно началось по-настоящему лишь в XV веке. До этого все величины выражались только словами. Алгебру тех времен называли, поэтому риторической, то есть словесной.
Во второй половинеXV века в Италии, Германии и других странах Европы были введены некоторые алгебраические символы и положено начало употреблению букв.
Арифметика учит общаться с числами и числовыми (арифметическими) выражениями, алгебра же — с буквами и алгебраическими выражениями, составленными из цифр, букв и знаков действий. Арифметическое выражение есть частный случай алгебраического.
Даем ученикам задание: При каких а уравнение имеет единственное решение?
Это задание вызовет у них затруднение, в плане того, каким способ решать его.
Рассмотрение способов решения задачи
Учащиеся рассматривают способы решения этого уравнения:
Обеспечим неотрицательность обеих частей,
возведем в квадрат обе части уравнения:
Найдем дискриминант квадратного уравнения:
1способ (Аналитический) По условию уравнение должно иметь один корень, значит,
а = — 49/8; , но надо проверить, удовлетворяет ли это значение ОДЗ:
Если D0, то только один корень уравнения должен удовлетворять условию
2 способ) Решим это задание графическим способом.
Проведем графический анализ менее трудоемкий, чем построение графика 
Рассмотрим схему расположения графиков при различных значениях а, причем с ростом а прямая у=2х – а перемещается вправо.

Когда прямая является касательной к полупараболе и, начиная с положения, когда прямая проходит через вершину параболы (- 3; 0),мы имеем одну точку пересечения, т. е одно решение исходного уравнения. Напишем уравнение касательной в точке х
Угловой коэффициент равен 2, т. е.
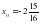
Тогда уравнение касательной 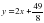
При х = — 3, у=0 графики пересекаются в двух точках. При этом а= — 6.
А при а — 6 имеем одну точку пересечения.
После рассмотренных решений можно заметить, что графический метод более рационален и удобен в применении.
Уравнение имеет единственное решение, если дискриминант равен нулю.
4а 2 -4а-24=0 Разделим обе части уравнения на 4
Ответ: при а = — 2; а = 3 уравнение имеет единственное решение.
Повторим схему исследования уравнений с параметрами:
Какие способы ее решения вы можете предложить? Таким образом, цель нашего занятия не просто научиться решать систему уравнений с параметрами , но и рассмотреть различные способы решения: аналитический и графический.
— Кто планирует решать эту систему аналитически? А кто предпочитает графический способ? Объединитесь, пожалуйста в группы по выбранному способу решения.
Ребята меняются местами и объединяются в группы, согласно выбранному способу решения.
— Группа, которая выбрала аналитический метод, запишут свое решение в тетрадях и мы рассмотрим его с помощью документ — камеры. А графический способ мы рассмотрим на интерактивной доске.
Вам дается минут 5-7 на решение.
После проверяются и анализируются решения, предложенные ребятами.
Теперь предлагаю вам еще одну систему уравнений. В чем вы заметили отличие?
— Кто сейчас выбирает группу аналитиков? А кто предпочитает графический способ? Объединитесь, пожалуйста в группы по выбранному способу решения.
— идет, возможно, переформирование групп.
В течении 10 минут ребята обсуждают решение. После чего снова оба решения проверяются.
Давайте рассмотрим еще один пример:
Найдите множество всех чисел 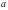
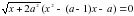
Решение. Перепишем данное уравнение в следующем виде:
Теперь важно не упустить, что 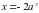
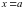
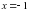
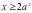
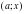
Ответ. При 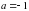
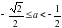
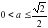
Как видим, и эту задачу рациональнее будет решать графическим методом.
Для закрепления дадим еще несколько уравнений с параметрами, при решении которых целесообразно использовать графический метод.
При каких значениях параметра 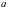
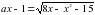
При каких 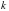
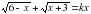
При каких значения параметра система имеет единственное решение
Попробуйте решить ее разными способами.
Сегодня мы с вами рассмотрели уравнения с параметрами решаемые двумя способами : аналитическим и графическим методом.
Как видим, используя этот метод, при решении задач, будут успешно формироваться поисковая и познавательная активность, а так же положительное эмоциональное отношение к познавательной и исследовательской деятельности.
Способы задания функции
Основной признак функциональной зависимости между двумя переменными величинами — это наличие соответствия между значениями этих величин: каждому допустимому значению одной переменной соответствует строго определённое значение другой.
Функция считается заданной, как только установлено соответствие между двумя переменными. Это соответствие может быть установлено различными способами. Рассмотрим подробнее три из них: аналитический, табличный и графический.
Аналитический способ
Аналитический способ — это способ задания функции с помощью формулы.
Например, формула y = x — 2 показывает, как с помощью значения аргумента x вычислить соответствующее ему значение функции y.
Табличный способ
Табличный способ — это способ задания функции с помощью таблицы со значениями.
Например, если измерять температуру воздуха каждый час в течении суток, то каждому часу (t) будет соответствовать определённая температура (T). Такое соответствие можно записать в виде таблицы:
| t (ч) | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| T (°) | 14 | 14 | 14,5 | 14,5 | 15 | 15 | 16 | 16 | 16 | 16,5 | 16,5 | 17 |
| t (ч) | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 |
| T (°) | 18 | 20 | 22 | 24 | 24,5 | 24,5 | 24 | 23 | 21 | 20 | 18 | 16 |
Следовательно, T функция от t — T(t) , определённая с помощью множества целых чисел от 0 до 24 и заданная таблицей. Соответствие между величинами двух переменных задаётся в данном случае не формулой, а таблицей.
Графический способ
Графический способ — это способ задания функции с помощью графика. В этом случае аргумент является абсциссой точки, а значение функции, соответствующее данному аргументу, ординатой.
Графики позволяют быстро находить значение функции по значению аргумента и наоборот — значение аргумента по значению функции. Например, рассмотрим уже готовый график функции:
Чтобы узнать, какое значение функции будет соответствовать аргументу x = 1, надо провести из соответствующей точки оси абсцисс (оси x) перпендикуляр на график. Ордината точки пересечения перпендикуляра с графиком (точки M) и будет соответствующим значением функции. Поэтому, так как точка M имеет координаты (1; 2), то запись этих значений в виде функции будет выглядеть так: y(1) = 2.
http://kopilkaurokov.ru/matematika/uroki/zaniatiie-eliektivnogho-kursa-razlichnyie-sposoby-rieshieniia-uravnienii-s-paramietrom-analitichieskim-i-ghrafichieskim-mietodom
http://izamorfix.ru/matematika/algebra/kak_zadat_funk.html