Решение тригонометрических уравнений графически
Уравнения, с которыми приходится сталкиваться при решении практических задач, как правило, значительно отличаются от тех, которые мы рассматривали. Для таких уравнений иногда вообще нельзя указать никакого способа, который позволял бы найти корни абсолютно точно. В таком случае приходится ограничиваться нахождением лишь приближенных значений корней. Современная математика располагает эффективными методами приближенного решения уравнений. Рассмотрим графический способ решения.
Пусть, например, нужно решить уравнение
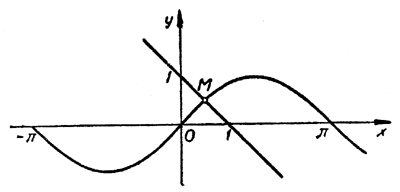
На одном и том же рисунке начертим два графика: график функции y = sin х и график функции у = 1 — х
Эти графики пересекаются в одной точке М. Абсцисса этой точки и дает нам единственный корень нашего уравнения:
Для уточнения полученного результата полезно использовать тригонометрические таблицы или компьютерные программы. При х = 0,5
следовательно, sin х 1 — х. Но тогда, как легко понять из того же рисунка, искомый корень x0 должен быть меньше, чем 0,6. Теперь уже мы знаем, что x0 находится в интервале [0,5; 0,6]. Поэтому с точностью до 0,1
С помощью таблиц можно найти приближенное значение x0 и с точностью до 0,01. Разделим интервал [0,5; 0,6] пополам. В средней точке (x = 0,55) этого интервала
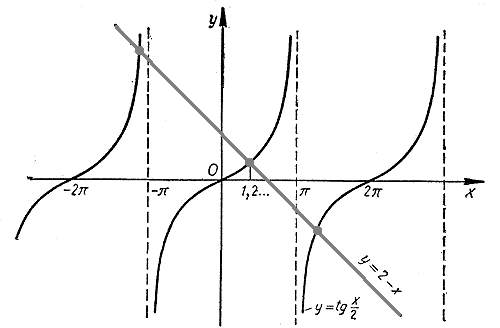
Графики функций у = tg x /2 и у = 2 — х пересекаются в бесконечном числе точек. Значит, данное уравнение имеет бесконечное множество корней. Найдем, например, наименьший положительный корень х0. Этот корень является абсциссой точки пересечения графиков. Примерно он равен 1,2.
Чтобы найти этот корень точнее, воспользуемся таблицами тангенсов В. М. Брадиса (или рассчитаем соответствующие значения в программе «Kалькулятор» или «Excel»). Выпишем значения функций у = tg x /2 и у = 2 — х в окрестности точки х = 1,2.
| x | 1,2 | 1,3 |
| y=tg x/2 | 0,6841 | 0,7602 |
| y=2-x | 0,8000 | 0,7000 |
| tg x/2-(2-x) | -0,1159 | 0,0602 |
Как видно из этой таблицы, при переходе от значения х = 1,2 к значению х = 1,3 разность tg x /2 — (2 — х) меняет свой знак на противоположный (с — на +). Значит, в нуль эта разность обращается где-то между значениями 1,2 и 1,3. Следовательно, с точностью до 0,1 х0 ≈ 1,2 (с недостатком) или х0 ≈ 1,3 (с избытком). Используя таблицу тангенсов, можно найти и приближенное значение этого корня
с точностью до 0,01. Для этого рассмотрим значение х = 1,25, являющееся средним значением чисел 1,2 и 1,3. При х = 1,25
Тригонометрические неравенства. Решение тригонометрических неравенств графическим способом. 10-й класс
Класс: 10
Презентация к уроку
Оборудование: ПК, проектор, экран, аудиторная доска.
Тип занятия: изучение нового материала.
| Образовательная цель: | сформировать навык решения тригонометрических неравенств, используя графический метод решения неравенств; отработать навыки построения графиков тригонометрических функций; познакомить учащихся с основоположниками тригонометрии и историей ее развития. |
| Развивающая цель: | обеспечить условия для развития умений анализировать, выделять главное, устанавливать единые общие признаки и свойства; научить применять знания на практике; научить критически оценивать свои знания. |
| Воспитательная цель: | воспитывать положительное отношение к знаниям; воспитывать дисциплинированность и добросовестность при выполнении заданий; воспитывать умение работать в парах (чувствовать индивидуальную ответственность за достижение результата). |
Задачи:
- повторить следующие темы по математике: решение квадратных неравенств графическим способом, преобразование графиков тригонометрических функций, понятие arcsin, arccos, arctg и arcctg числа, решение тригонометрических уравнений;
- научить применять графический метод для решения тригонометрических неравенств;
- отработать навыки построения графиков тригонометрических функций;
- расширить кругозор учащихся об истории развития Тригонометрии;
- для активизации познавательной деятельности учащихся применять различные формы и методы работы на уроке: фронтальная, индивидуальная и групповая (работа в парах) формы работы, использование игровых технологий.
Структура занятия:
- Организационный момент, проверка домашнего задания (3 мин.);
- Актуализация опорных знаний и фиксация затруднений в деятельности (5 мин.);
- Объяснение нового материала (10 мин.);
- Экспертная работа (5 мин.);
- Самостоятельная работа в парах (10 мин.);
- Домашнее задание (2 мин.);
- Игра “Поле чудес” (6 мин.);
- Рефлексия деятельности (итог урока) (4 мин.).
Пояснение к уроку: во время урока учащиеся выставляют баллы в “Рабочую карту урока” согласно правилам, описанным в данной карте. В конце урока подводится итог работы учащихся по количеству набранных баллов.
1. Организационный момент, проверка домашнего задания
Французский писатель Анатоль Франс однажды заметил: “Учиться можно только весело… Чтобы переваривать знания, надо поглощать их с аппетитом.”.
Давайте сегодня на уроке будем следовать этому совету писателя, будем активны, внимательны, будем поглощать знания с большим желанием.
Прежде чем приступить к изучению нового материала, проверим домашнее задание на сегодня.
Проверка домашнего задания:
№ 11.27 (а, б), № 11.29 (б, е), № 11.30 (б)
Никольский С. М. Алгебра и начала математического анализа. 10 класс – М.: Просвещение, 2013.
За каждое правильно выполненное задание – 1 балл в рабочую карту занятия в колонку “Домашняя работа”.
2. Актуализация опорных знаний и фиксация затруднений в деятельности
Тема нашего урока – Тригонометрические неравенства. Решение тригонометрических неравенств графическим способом.
Давайте запишем дату и тему урока в тетрадь.
Перед Вами на сегодня стоит задача – научиться применять графический метод для решения тригонометрических неравенств.
Поработаем сначала устно, чтобы вспомнить те понятия и приемы, которые нам понадобятся для изучения новой темы.
За каждый правильный ответ учащиеся получают 1 балл в рабочую карту занятия в колонку “Устная работа”.
Инструкция по работе с презентацией: при подведении курсора к ответу и нажатии левой кнопки мыши: неверные ответы исчезают, а в области верного ответа всплывает окно со словом “Верно”.
3. Объяснение нового материала
Если вспомнить определение тригонометрического уравнения – это уравнение, содержащее переменную под знаком тригонометрической функции, тогда легко можно дать определение тригонометрического неравенства – это неравенство, содержащие переменную под знаком тригонометрической функции.
Для решения тригонометрических неравенств мы будем использовать графический метод.
Рассмотрим решение неравенства
Построим график функции: 

Определим точки пересечения данных графиков:
Заштрихуем область, при которой значения функции 

Так как функция 


Ответ: 
Рассмотрим решение неравенства
Пусть 
Рассмотрим графики функций 



Получим неравенство
Следовательно,
Ответ: 

4. Экспертная работа
К доске приглашаются двое учащихся, хорошо разобравшихся в материале и желающих ответить у доски, они будут выступать в роли экспертов, остальные учащиеся могут поправлять их решение по мере надобности с места.
1. 

2. 

За работу у доски учащиеся получают 1-3 балла, за работу с места 1 балл.
5. Самостоятельная работа в парах
Прежде чем перейти к выполнению самостоятельной работы, необходимо заметить, что при решении более сложных тригонометрических неравенств, их с помощью преобразований сводят к простейшим тригонометрическим неравенствам, используя при этом те же приёмы, что и при решении тригонометрических уравнений.
Учащиеся выполняют задание, обмениваются тетрадями и проверяют работу соседа по парте, выставляя соответствующие баллы, ответы представлены на экране, подробное решение неравенств под номером 3 необходимо заранее подготовить на аудиторной доске.
Для решения тригонометрических неравенств графическим методом можно использовать Приложение № 2 к данному уроку.
| Вариант № 1 Решить неравенства | Вариант № 2 Решить неравенства |
1.  | 1.  |
2.  | 2.  |
 |   |
За каждое верное задание № 1,2-1 балл, № 3 – 3 балла.
Подведение итогов изучения новой темы. Учащимся необходимо ответить на вопросы учителя.
Вопросы:
- Какой метод мы использовали для решения тригонометрических неравенств?
- Что необходимо предпринять, чтобы решить тригонометрическое неравенство графическим способом?
- Как влияет периодичность тригонометрических функций на ответ при решении тригонометрических неравенств?
За каждый правильный ответ учащиеся получают 1 балл в рабочую карту занятия в колонку “Устная работа”.
6. Домашнее задание
Никольский С. М. Алгебра и начала математического анализа. 10 класс – М.: Просвещение, 2013.
п. 11.5, 11.6, № 11.34 (б), 11.36 (в), 11.37 (в), 11.38 (б), 11.41 (б)
Дополнительное задание (по желанию):
Решить неравенство
7. Игра “Поле чудес”
Игра построена по принципу одноименной телевизионной игры. Учитель читает задание, учащиеся могут открыть любую букву, если выполнят скрытое в данной ячейке задание.
За каждую угаданную букву (решенное задание) учащиеся получают 1 балл, за отгаданное слово – 5 баллов.
Инструкция по работе с презентацией: при подведении курсора к ячейке, за которой скрывается буква, и нажатии левой кнопки мыши: появляется задание, которое необходимо выполнить, при повторном нажатии левой кнопки мыши в данную область появляется скрытая там буква.
Древнегреческий астроном, географ и математик II века до н.э., часто называемый величайшим астрономом античности. Главной заслугой его считается то, что он привнёс в греческие геометрические модели движения небесных тел предсказательную точность астрономии Древнего Вавилона.
При разработке теорий Луны и Солнца он использовал античный вариант тригонометрии. Возможно, он первым составил таблицу хорд, аналог современных таблиц тригонометрических функций.
Швейцарский, немецкий и российский математик, внёсший значительный вклад в развитие математики, а также механики, физики, астрономии и ряда прикладных наук.
Автор более чем 800 работ по математическому анализу, дифференциальной геометрии, теории чисел, приближённым вычислениям, небесной механике, математической физике, оптике, баллистике, кораблестроению, теории музыки и др.
Почти полжизни провёл в России, где внёс существенный вклад в становление российской науки. С 1731 по 1741, а также с 1766 года был академиком Петербургской Академии Наук (в 1741—1766 годах работал в Берлине, оставаясь одновременно почётным членом Петербургской Академии). Хорошо знал русский язык и часть своих сочинений (особенно учебники) публиковал на русском. Первые русские академики-математики (С.К. Котельников) и астрономы (С.Я. Румовский) были его учениками.
Аналитическая теория тригонометрических функций в основном была создана этим выдающимся математиком XVIII века. Именно он первым ввел известные определения тригонометрических функций, стал рассматривать функции произвольного угла, получил формулы приведения.
Ответ: Леонард Эйлер
Наука об измерении треугольников. Данный термин впервые появился в 1595 г. как название книги немецкого математика Бартоломеуса Питискуса, а сама наука ещё в глубокой древности использовалась для расчётов в астрономии, геодезии и архитектуре..
Раздел математики, в котором изучаются тригонометрические функции и их приложения к геометрии.
Рефлексия деятельности (итог урока)
Рабочая карта занятия
о/т — оценка товарища, о/у- оценка учителя, с/о – самооценка, о/г-оценка группы
с/о
Общее количество баллов, по 1 за каждое правильно выполненное задание.
о/у
Общее количество баллов, по 1 за каждый правильный ответ.
о/г
1-3 балла за работу у доски,
1 балл за работу с места.
о/т
За каждое верное задание
№ 3 – 3 балла.
о/у
Общее количество баллов, по 1 за каждый правильный ответ, за отгаданное слово – 5 баллов.
- 16 и более баллов – оценка “5”
- 11 — 15 баллов – оценка “4”
- 6 — 10 баллов – оценка “3”
Литература:
- Никольский, С.М. Алгебра и начала математического анализа. 10 класс: учеб. для общеобразоват. учреждений: базовый и профил. уровни/ С. М. Никольский, М.К. Потапов, Н.Н. Решетников, А.В. Шевкин. – М.: Просвещение, 2013.
- Чулков, П.В. Материалы курса “Уравнения и неравенства в школьном курсе математики”: Лекции 5-8./ П.В. Чулков. – М.: Педагогический университет “Первое сентября”, 2010.
- Егерев, В.К. Сборник задач по математике для поступающих во втузы: учеб. пособие/ В.К. Егерев, Б.А. Кордемский, В.В. Зайцев и др.; Под ред. М.И. Сканави. – М.: “Столетие”, 1997.
Графический метод решения тригонометрических уравнений и неравенств Текст научной статьи по специальности « Математика»
Аннотация научной статьи по математике, автор научной работы — Чекмарева И. А.
Актуальность представленной работы заключается в практической направленности предлагаемого метода, поскольку графическое решение тригонометрических уравнений и неравенств дает возможность определить корни намного проще, чем при аналитическом методе.
Похожие темы научных работ по математике , автор научной работы — Чекмарева И. А.
Текст научной работы на тему «Графический метод решения тригонометрических уравнений и неравенств»
ГРАФИЧЕСКИМ МЕТОД РЕШЕНИЯ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ И НЕРАВЕНСТВ
Краснодарский гуманитарно-технологический колледж, г. Краснодар
Актуальность представленной работы заключается в практической направленности предлагаемого метода, поскольку графическое решение тригонометрических уравнений и неравенств дает возможность определить корни намного проще, чем при аналитическом методе.
Преимущество метода заключается в том, что он не требует особых технических навыков в тригонометрических преобразованиях, а теоретическую сторону дела позволяет продемонстрировать очень наглядно. Конечно, при графическом решении уравнений корни определяются приближенно, но, тем не менее, той точности, которую обеспечивает графический метод, бывает вполне достаточно для решения практических задач.
Пусть необходимо решить уравнение Ffcos t; sin t) = 0 (1), где F(x, у) -многочлен от двух переменных х и у. Идея решения состоит в том, чтобы дополнить уравнение (1) тождеством cos2t + sin2t = 1, ввести обозначение х = tos t, у = sin t и решить графически систему, состоящую из двух уравне-
„ \F(x; y) = 0 ний: i 2 2
Получим точки пересечения (если они существуют) единичной окружности с графиком функции Ffo у), координаты которых определить не сложно. Но в этом нет никакой необходимости. Для того, чтобы найти корни уравнения (1), достаточно измерить углы между положительным направлением оси Ох и радиус-векторами полученных точек пересечения графиков с помощью транспортира: t1 и а1, t2 и а2 (рис. 1). Учитывая периодичность
* Технологическое отделение. Научный руководитель: Андрюхина М.И., преподаватель математики.
тригонометрических функций, получим окончательный ответ: tj и а\ + 360° n, t2и а2 + 360° к, где n e Z, к e Z.
содержащей два уравнения:
Рассмотрим уравнение F(ctg t; tg t) = 0 (2). Дополним его тождеством ctg t • tg t = 1 и введем обозначения х = ctg t, у = tg t. Мы пришли к системе,
Решая графически эту систему, получим точки пересечения (если они существуют) ветвей гиперболы ху = 1 с графиком уравнения F(x; у) = 0.
Для нахождения решения уравнения (2) достаточно спроецировать полученные точки пересечения графиков на линию тангенсов, т.е. на прямую х = 1, и определить с помощью транспортира углы между положительным направлением оси Ох и радиус-векторами построенных проекций (рис. 2): t1 и а1, t2 и а2. Учитывая периодичность тригонометрических функций, получим окончательный ответ: t1 и а1 + 180° n, t2 и а2 + 180° к, где n e Z, к e Z.
1. Решим уравнение соб t = 2sm t — 1.
Введем обозначение х = oos t, у = sin t и введем вспомогательную систему:
J x = 2y-1 Ix2 + y2 = 1
Преобразуем ее следующим образом: ,
(У = log2(x +1) I X2 + y2 = 1 • Графическое решение системы показано на рис. 3.
Проведя радиус-векторы точек пересечения единичной окружности с графиком функции у = log2(x + 1), получим tx и -117°, t2 и 48°. С учетом периодичности: t1 и -117 ° + 360° n, t2 и 48° + 360° к, где n e Z, к e Z. 2. Пусть дано уравнение 8 tg t — 4 ctg2 t — 4 ctg t + 23 = 0.
Введем обозначение х = ctg t, у = tg t, перепишем уравнение в новых обозначениях: 8у — 4-х2 — 4х + 23 = 0 и приведем его к виду: у = 0,5(х + 0,5)2 — 3.
Гy = 0,5(х + 0,5)2 -3 Решим графически систему: ^ .
По рисунку 4 находим, что ti и -71°, t2 и -20°, t3 и 25°. С учетом периодичности: ti « -71° + 360° n, t2 и -20° + 360° к, t3 и 25° + 360°m, п e Z, к e Z, m e Z.
3. Перейдем к неравенству:
8 eos3/ — 14 cos2t + 6 eos t — 2 sin2t + 8 sin t — 3 > 0.
Заменим sin2t на 1 — eos2t и введем обозначения х = eos t, у = sin t. Это позволит привести неравенство к виду у > -(х — 0,5)3 + 0,5.
Решим графически систему: ^ , , .
Дуга АВ единичной окружности и является графическим решением этой вспомогательной системы (рис. 5). Каждая точка этой дуги имеет радиус-вектор, образующий с положительным направлением оси Ох угол, величина которого изменяется в промежутке [26°; 106°].С учетом периодичности получим: t е [26° + 360° к; 106°+ 360° к], где к е Z.
-lf 0 /юе ‘хЗйшШШШШШШШШ ¡^^стмммжщ
— 0.S)3у 0,5 plllllll ■1 11111111 1
4. Решим неравенство 2 tg t + ctg2 t — 2 ctg t — 4 Надоели баннеры? Вы всегда можете отключить рекламу.
http://urok.1sept.ru/articles/658051
http://cyberleninka.ru/article/n/graficheskiy-metod-resheniya-trigonometricheskih-uravneniy-i-neravenstv