Графическое решение систем линейных уравнений
Презентация к уроку
Цели и задачи урока:
- продолжить работу по формированию навыков решения систем уравнений графическим методом;
- провести исследования и сделать выводы о количестве решений системы двух линейных уравнений;
- развивать интерес к предмету через игру.
1. Организационный момент (Планерка) – 2 мин.
– Добрый день! Начинаем нашу традиционную планерку. Мы рады приветствовать всех, кто сегодня у нас в гостях, в нашей лаборатории (представляю гостей). Наша лаборатория называется: «ТРУД с интересом и удовольствием» (показываю слайд 2). Название служит девизом в нашей работе. «Твори, Решай, Учись, Добивайся с интересом и удовольствием». Дорогие гости, представляю вам руководителей нашей лаборатории (слайд 3).
Наша лаборатория занимается изучением научных трудов, исследованиями, экспертизой, работает над созданием творческих проектов.
Сегодня тема нашего обсуждения: «Графическое решение систем линейных уравнений». (Предлагаю записать тему урока)
Программа дня: (слайд 4)
1. Планерка
2. Расширенный ученый совет:
- Выступления по теме
- Допуск к работе
3. Экспертиза
4. Исследования и открытия
5. Творческий проект
6. Отчет
7. Планирование
2. Опрос и устная работа (Расширенный ученый совет) – 10 мин.
– Сегодня мы проводим расширенный ученый совет, на котором присутствуют не только руководители отделов, но и все члены нашего коллектива. Лаборатория только начала работу по теме: «Графическое решение систем линейных уравнений». Мы должны постараться добиться самых высоких достижений в этом вопросе. Наша лаборатория должна славиться качеством исследований по этой теме. Я, как старший научный сотрудник, желаю всем удачи!
Результаты исследований будут сообщены начальнику лаборатории.
Слово для доклада о решении систем уравнений имеет…(вызываю ученика к доске). Даю заданию задание (карточка 1).
А лаборант…(называю фамилию) напомнит, как строить график функции с модулем. Даю карточку 2.
Карточка 1 (решение задания на слайде 7)
Решить систему уравнений:
Карточка 2 (решение задания на слайде 9)
Построить график функции: y = | 1,5x – 3 |
Пока сотрудники готовятся к докладу, я проверю, как вы готовы к выполнению исследований. Каждый из вас должен получить допуск к работе. (Начинаем устный счет с записью ответов в тетрадь)
Допуск к работе (задания на слайдах 5 и 6)
1) Выразить у через x:
3x + y = 4 (y = 4 – 3x)
5x – y = 2 (y = 5x – 2)
1/2y – x = 7 (y = 2x + 14)
2x + 1/3y – 1 = 0 (y = – 6x + 3)
2) Решить уравнение:
5x + 2 = 0 (x = – 2/5)
4x – 3 = 0 (x = 3/4)
2 – 3x = 0 (x = 2/3)
1/3x + 4 = 0 (x = – 12)
3) Дана система уравнений:
Какая из пар чисел (– 1; 1) или (1; – 1) является решением данной системы уравнений?
Сразу после каждого фрагмента устного счета учащиеся обмениваются тетрадями (с рядом сидящим учеником в одном отделе), на слайдах появляются верные ответы; проверяющий ставит плюс или минус. По окончании работы начальники отделов вносят результаты в сводную таблицу (см ниже); за каждый пример дается 1 балл (возможно получить 9 баллов).
Те, кто набрал 5 и более баллов, получают допуск к работе. Остальные получают условный допуск, т.е. должны будут работать под контролем начальника отдела.
Таблица (заполняет начальник)
| п/п | Фамилия | Допуск | Экспертиза | Исследования | Проект | Всего |
| 1 | Климов | |||||
| Бадин | ||||||
| Бережная | ||||||
| Ждан | ||||||
| Мацкевич |
(Таблицы выдаются до начала урока)
После получения допуска слушаем ответы учащихся у доски. За ответ ученик получает 9 баллов, если ответ полный (максимальное количество при допуске), 4балла, если ответ не полный. Баллы вносят в графу «допуск».
Если на доске правильное решение, то слайды 7 и 9 можно не показывать. Если решение правильное, но нечетко выполненное или решение неправильное, то слайды демонстрируются обязательно с пояснениями.
Слайд 8показываю обязательно после ответа ученика по карточке 1. На этом слайде выводы важные для урока.
Алгоритм решения систем графическим способом:
- Выразить y через x в каждом уравнении системы.
- Построить график каждого уравнения системы.
- Найти координаты точек пересечения графиков.
- Сделать проверку (обращаю внимание учащихся на то, что графический метод обычно дает приближенное решение, но в случае попадания пересечения графиков в точку с целыми координатами, можно выполнить проверку и получить точный ответ).
- Записать ответ.
3. Упражнения (Экспертиза) – 5 мин.
Вчера в работе некоторых сотрудников были допущены грубые ошибки. Сегодня вы уже более компетентны в вопросе графического решения. Вам предлагается провести экспертизу предложенных решений, т.е. найти ошибки в решениях. Демонстрируется слайд 10.
Работа идет в отделах. (На каждый стол выдаются ксерокопии заданий с ошибками; в каждом отделе сотрудники должны найти ошибки и подчеркнуть их или исправить; ксерокопии сдать старшему научному сотруднику, т.е. учителю). Тем, кто найдет и исправит ошибку, начальник добавляет 2 балла. Затем обсуждаем допущенные ошибки и указываем их на слайде 10.
Ошибка 1
Решить систему уравнений:
Ответ: решений нет.
Учащиеся должны продолжить прямые до пересечения и получить ответ: (– 2; 1).
Ошибка 2.
Решить систему уравнений:
Учащиеся должны найти ошибку в преобразовании первого уравнения и исправить на готовом чертеже. Получить другой ответ: (2; 5).
4. Объяснение нового материала (Исследования и открытия) – 12 мин.
Учащимся предлагаю решить графически три системы. Каждый ученик решает самостоятельно в тетради. Консультироваться могут только те, у кого условный допуск.
Решение
Без построения графиков понятно, что прямые совпадут.
На слайде 11 показано решение систем; ожидаемо, что учащиеся будут испытывать затруднение при записи ответа в примере 3. После работы в отделах проверяем решение (за верное начальник добавляет 2 балла). Теперь пришло время обсудить, сколько решений может иметь система двух линейных уравнений.
Учащиеся должны сделать выводы самостоятельно и объяснить их, перечислив случаи взаимного расположения прямых на плоскости (слайд 12).
5. Творческий проект (Упражнения) – 12 мин.
Задание дается для отдела. Начальник дает каждому лаборанту по способностям фрагмент его выполнения.
Решить системы уравнений графически:
После раскрытия скобок учащиеся должны получить систему:
После раскрытия скобок первое уравнение имеет вид: y = 2/3x + 4.
6. Отчет (проверка выполнения задания) – 2 мин.
После выполнения творческого проекта учащиеся сдают тетради. На слайде 13 показываю то, что должно было получиться. Начальники сдают таблицу. Последнюю графу заполняет учитель и ставит отметку (отметки можно сообщить ученикам на следующем уроке). В проекте решение первой системы оценивается тремя баллами, а второй – четырьмя.
7. Планирование (подведение итогов и домашнее задание) – 2 мин.
Подведем итоги нашего труда. Мы неплохо поработали. Конкретно о результатах поговорим завтра на планерке. Безусловно, все без исключения лаборанты овладели графическим методом решения систем уравнений, усвоили, какое количество решений может иметь система. Завтра каждого из вас ждет персональный проект. Для дополнительной подготовки: п.36; 647-649(2); повторите аналитические методы решение систем. 649(2) решите и аналитическим методом.
Нашу работу в течение всего дня контролировал директор лаборатории Ноумэн Ноу Мэнович. Ему слово. (Показываю заключительный слайд).
Как решать системы уравнений с двумя переменными
Что такое система уравнений с двумя переменными
Системой уравнений в алгебре называется некое условие, смысл которого заключается в одновременном выполнении нескольких уравнений относительно нескольких (либо одной) переменных.
Это значит, что система представляет собой комплекс уравнений. Данные равенства могут содержать одну, две или более переменных. Основным условием понятия «система уравнений» является то, что все эти уравнения выполняются в одно время.
Объединить уравнения в систему можно с помощью фигурной скобки:
У р а в н е н и е 1 У р а в н е н и е 2 У р а в н е н и е 3 …
Графический метод решения
Принцип решения систем уравнений графическим способом заключается в построении графиков для каждого уравнения в общей системе координат. Тогда решения системы соответствуют точкам, в которых данные графики пересекаются. После объяснения решения ответ принято записывать, как координаты этих точек.
Разберем наглядный пример. Предположим, что дана некая система уравнений, решать которую нужно графическим способом. Выполним работу последовательно:
- Запишем систему.
- Выразим одну из переменных (пусть это будет у).
- Построим на координатной прямой графики функций.
- Найдем точки пересечения графиков.
2 x + 3 y = 12 3 x — y = 7 ⇔ y = 4 — 2 3 x y = 3 x — 7
Заметим, что точка пересечения графиков имеет следующие координаты:
Графический метод решения систем уравнений уступает в точности другим способам. Использовать график целесообразно в том случае, когда в задаче записана система линейных уравнений. Подобные задачи встречаются в средних классах школы. Такие уравнения имеют вид y = a x + b без квадратных членов, а их графики являются прямыми.
Метод подстановки
Алгоритм решения системы уравнений с помощью метода подстановки:
- выражение одной переменной через другие;
- подстановка выражения, которое получилось, в начальные уравнения на место выраженной переменной;
- повторение второго шага до тех пор, пока не будут определены другие переменные.
Рассмотрим последовательность действий на практике. Предположим, что имеется некая система уравнений, которую требуется решить:
2 x + 3 y = 12 3 x — y = 7
Выразим у из второго уравнения:
Выполним подстановку полученного выражения в первое равенство:
2 x + 3 3 x — 7 = 12
Для полученного уравнения с одной переменной несложно найти корни:
2 x + 3 3 x — 7 = 12
2 x + 3 · 3 x — 3 · 7 = 12
2 x + 9 x — 21 = 12
Зная х, выполним подстановку и найдем у:
y = 3 x — 7 = 3 · 3 — 7 = 2 .
Запишем в ответ значения двух переменных.
Ответ: x = 3 ; y = 2 , либо (3;2).
Метод сложения
При сложении левых частей пары (или более) уравнений выражение, полученное в результате, равно сложенным правым частям этих же равенств, согласно формуле:
a = b c = d ⇒ a + c = b + d
В обратную сторону записанное свойство не работает:
a + c = b + d ◃ ≠ ▹ a = b c = d
Таким образом, при решении систем уравнений можно увеличивать обе части уравнения на одинаковое число. Например, сложим первое уравнение с числом с:
a = b c = d ⇒ a + c = b + c
Исходя из того что c=d, можно выполнить замену c на d справа:
a = b c = d ⇒ a + c = b + c ⇒ a + c = b + d .
В качестве примера попробуем решить систему уравнений:
2 x + y = 12 3 x — y = 3
Следуя правилу, суммируем уравнения. В процессе левые части складываем друг с другом. Аналогичным образом поступим с правыми частями равенств. В результате:
2 x + y = 12 3 x — y = 3 ⇒ 2 x ¯ ¯ + y ¯ + 3 x ¯ ¯ — y ¯ = 15 ⇔ 5 x = 15 ⇔ x = 3 .
Получилось избавиться от переменной у. В итоге задача значительно упростилась. Подставим число 3 на место слагаемого с х:
2 x + y = 12 x = 3 ⇔ 2 · 3 + y = 12 x = 3 ⇔ y = 6 x = 3
В следующем примере система уравнений имеет следующий вид:
2 x + 3 y = 13 4 x + 5 y = 23
Заметим, что с помощью сложения задание не получится упростить. В этом случае можно воспользоваться умножением уравнения на какое-либо число, отличное от нуля. Важно выбрать такой множитель, который позволит избавиться от одной из переменных. В этом случае лучше использовать (-2):
2 x + 3 y = 13 · — 2 4 x + 5 y = 23 ⇔ — 4 x — 6 y = — 26 4 x + 5 y = 23
Приступим к сложению:
— 4 x — 6 y = — 26 4 x + 5 y = 23 ⇒ — 4 x — 6 y + 4 x + 5 y = — 26 + 23 ⇔ — y = — 3 ⇔
Выполним подстановку у=3 в первое уравнение:
2 x + 3 y = 13 y = 3 ⇔ 2 x + 9 = 13 y = 3 ⇔ x = 2 y = 3
Задания для самостоятельного решения
Нужно решить систему уравнений:
13 x + 6 y = 7 2 x — 4 y = 6
Выразим х с помощью второго уравнения:
Найти значения переменных:
2 x + 5 y = 10 8 y — 5 x = 57
Из первого равенства выразим х:
2 x + 5 y = 10 2 x = 10 — 5 y
Подставим полученное значение во второе уравнение и запишем ответ.
Дана система уравнений, которую требуется решить:
2 x + 5 y = 10 3 x — 2 y = 1
В данном случае следует умножить первое уравнение на число 2, а второе равенство умножить на число 5:
2 x + 5 y = 10 · 2 3 x — 2 y = 1 · 5 ⇔ 4 x + 10 y = 20 15 x — 10 y = 5
После сложения уравнений остается лишь определить х:
19 x = 25 ⇔ x = 25 19
При подстановке х в какое-либо из двух уравнений можно вычислить у и записать ответ.
Ответ: ( 25 19 ; 28 19 ) .
Требуется найти переменные:
3 y — 4 x = — 13 3 x + 7 y = 56
Здесь следует в первую очередь найти произведение первого уравнения и числа 3, умножить второе уравнение на множитель 4. Далее остается суммировать уравнения и записать ответ.
Нужно решить систему уравнений:
7 x + 3 y = 21 4 y — 5 x = — 15
Множителем для первого уравнения является число 4. Второе уравнение нужно умножить на -3. Полученные равенства следует сложить и записать ответ.
Решить систему уравнений:
6 x — 8 y = — 2 9 x + 10 y = 8
В данном случае предполагается умножение уравнений на дробные числа. Множителем для первого уравнения является дробь 1 4 . Второе уравнение следует умножить на 1 5 :
6 x — 8 y = — 2 · 1 4 9 x + 10 y = 8 · 1 5 ⇔ 6 4 x — 2 y = — 1 2 9 5 x — 2 y = 8 5
Далее выполним сложение:
6 4 x — 2 y = — 1 2 9 5 x — 2 y = 8 5 ⇔ 3 2 x + 9 5 x =-0,5+1,6 ⇔ ⇔ 15 10 x + 18 10 x = 1,1 ⇔ 33 10 x = 1 , 1 ⇔ ⇔ 33 = 11 x x = 3
Путем подстановки определим y:
6 3 — 8 y = — 2 x = 3 ⇔ — 8 y = — 4 x = 3 ⇔ y = 2 x = 3
Найти корни следующих систем уравнений:
2 x + 3 y = 11 3 x + 2 y = 9
3 x — y = 85 5 x + 2 y = 17
x — 3 y = 6 2 y — 5 x = — 4
y 4 — x 5 = 6 x 15 + y 12 = 0
y — x = 5 x + 3 y = 3
Ответ: (1; 3), (17; -34), (0; -2), (-15; 12), (-3; 2).
Урок «Система линейных уравнений. Графическое решение системы»
Краткое описание документа:
Во многих случаях, особенно связанных с решением практических задач, приходится сталкиваться с такой математической конструкцией, как система уравнений. В таких случаях задача базируется на заданных двух переменных, участвующих в построении двух равенств. В новом видеоуроке подробно изучим подобную систему.
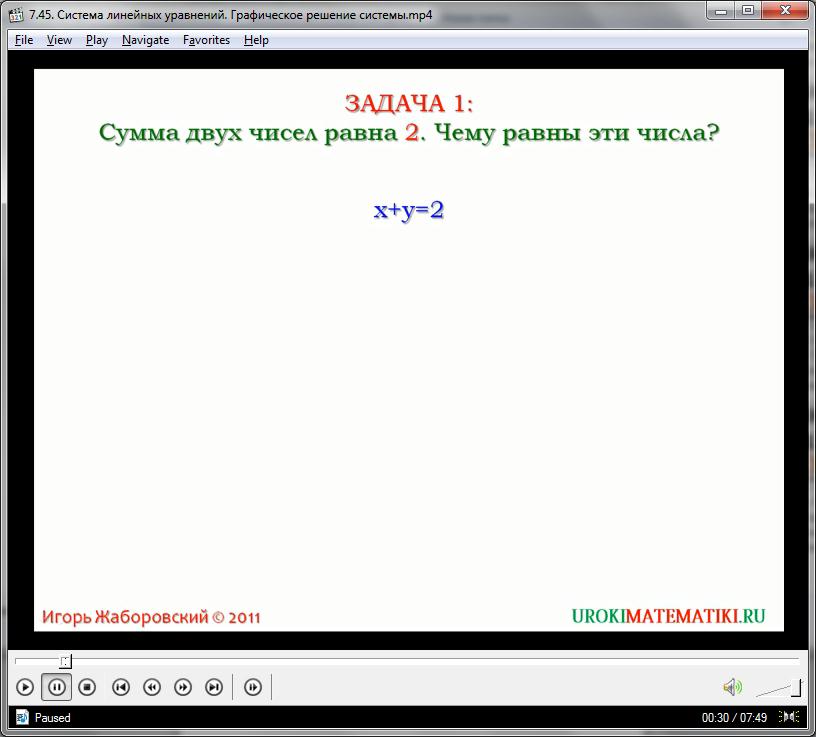
Предположим, у нас есть такое упражнение. Сумма двух неизвестных чисел равна двум. Чему равны эти числа? Алгебраически, условие задачи легко отображается линейным уравнением с двумя переменными:
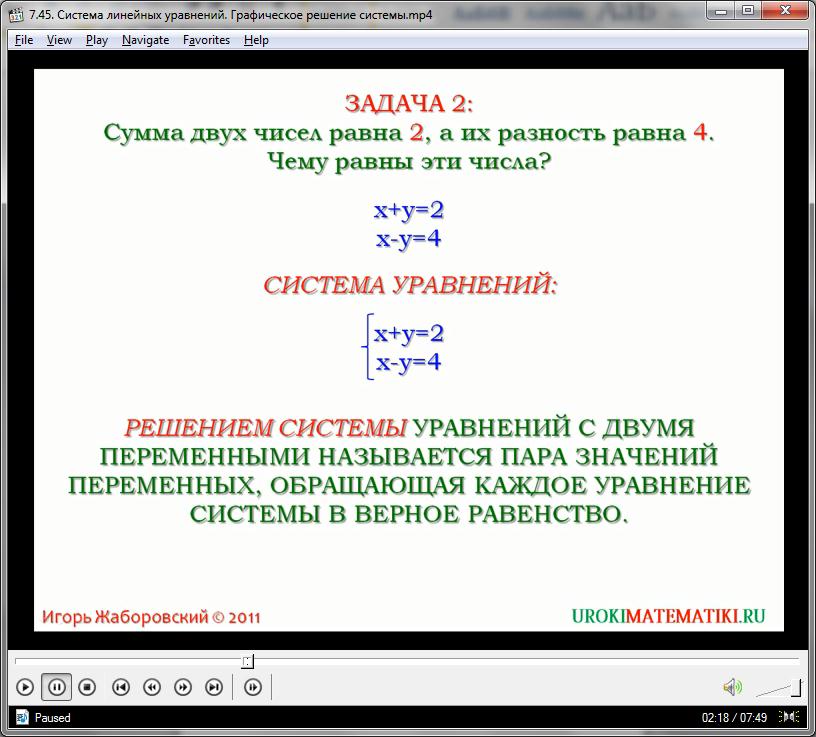
Данное уравнение имеет бесконечное множество решений. Напомним, что ответом, в данном случае, всегда будет пара неких чисел, представляющих собой взаимосвязанные значения х и у. Чтобы сократить количество корней уравнения, зададим ещё одно условие. Пусть наши числа не только дают сумму, равную двум, но и разность, равную четырем:
При этом стоит обратить внимание, что значения каждой из переменных строго коррелируют между уравнениями, то есть, ответ для них будет общим. Такая пара уравнений, имеющая две переменные и общую пару значений, являющихся ответом, называется системой линейных уравнений:
На письме сбоку от пары уравнений записывается обобщающая фигурная скобка. Важно понимать, что пара значений х и у в ответе должна преобразовывать в правильное равенство и первое, и второе уравнения, иначе она не будет являться корректным корнем для этой системы.
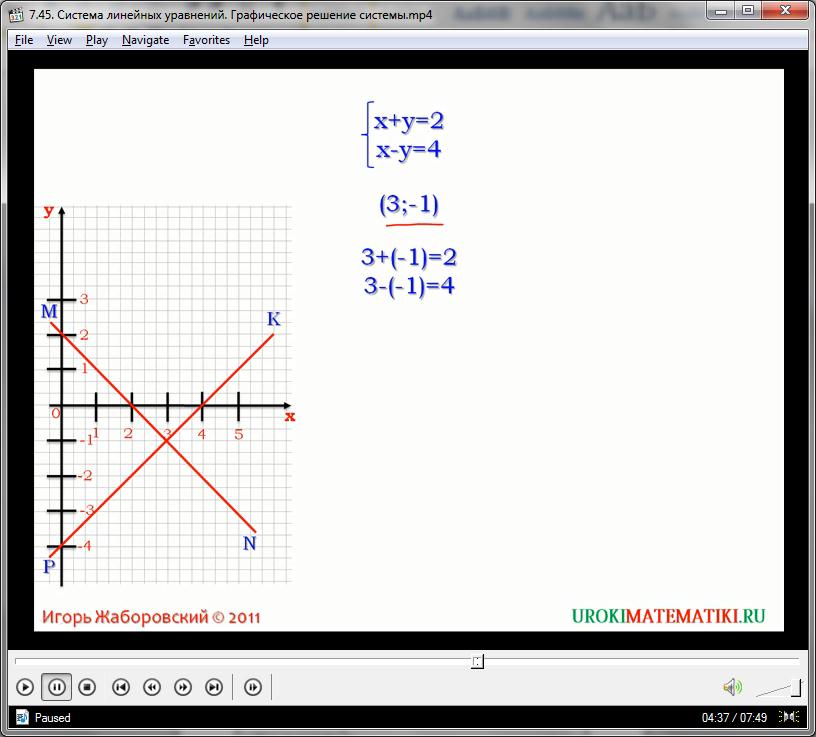
Системы линейных уравнений имеют несколько основных способов решения. В данном случае, в нашем видеоуроке мы разберем графический метод. Для этого преобразуем систему в набор функций (или зависимостей) при помощи тождественных равносильных преобразований:
Наши функции являются простейшими случаями прямолинейной зависимости. Графики для них строятся довольно легко на основании двух любых точек, которые рассчитываются в координационной сетке. Итак, построив графики для обеих определенных зависимостей, мы увидим, что это прямые, которые не проходят через центр координат, но при этом, однократно пересекаются друг с другом. Точка пересечения имеет координаты (3, -1). Подставим аргумент и значение зависимости в нашу систему уравнений, вместо х и у соответственно:
Образовались верные равенства, а значит, пара 3, -1 удовлетворяет систему уравнений, как пара корней. Таким образом, для того, чтобы решить подобную систему, необходимо совершить такой алгоритм действий:
1. Преобразовать уравнения в линейные зависимости, использовав тождественные изменения;
2. Составить координационную сетку хотя бы для двух точек каждого из двух графиков;
3. Отобразить в декартовой системе координат графики обеих зависимостей;
4. Найти точку пересечения графиков (если она есть), и записать её координаты как корни системы уравнений, где аргумент – это х, а значение зависимости – это у.
Следует понимать, что каждое отдельное уравнение с двумя переменными – это линейная зависимость, которую можно отобразить на графике. Она показывает множество связей между парами х и у. И если по самому определению для системы уравнений нужна одно общее решение, то логично искать такие значения х и у, которые будут одновременно соответствовать обоим графикам зависимости.
Особенности пересечения графиков отображают, помимо того, диапазон возможных вариантов решения системы уравнений. При наличии одной точки пересечения (как в случае с двумя прямыми) – решение системы лишь одно, и оно соответствует этой точке. Если пересечений нет – значит, система уравнений не имеет решений вообще (так как при этом не существует общих элементов в двух парах множества). Ну а если прямые совпадают и пересечение вырождается в сливание – ответами на подобную систему будет бесконечное множество чисел, так как любая прямая охватывает бесконечность.
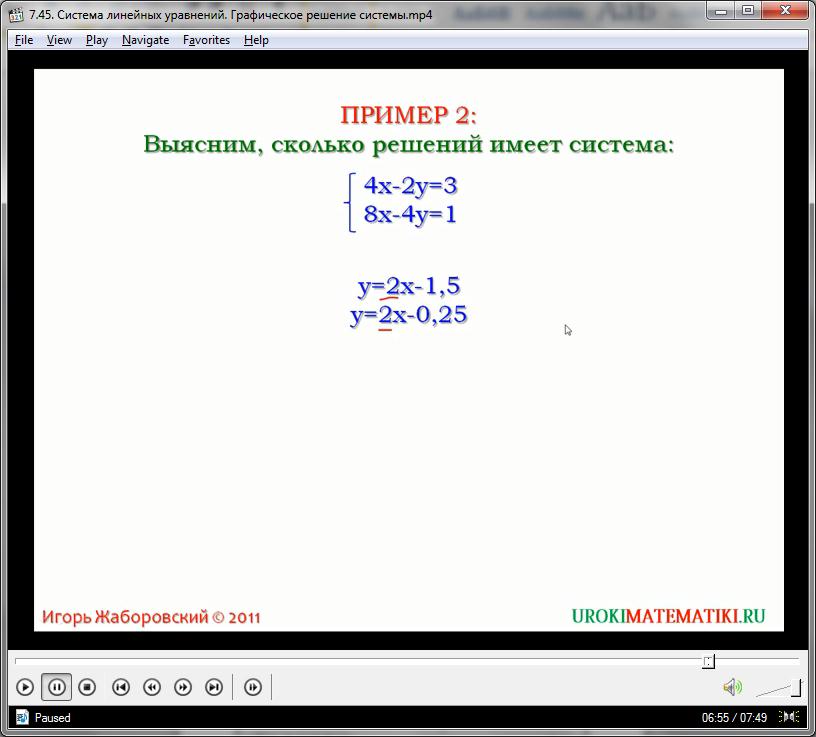
Иногда можно определить наличие корней только лишь по анализу самих уравнений, без применения построения графиков. Рассмотрим пример:
Преобразуем уравнения так, чтобы вывести линейные зависимости, использовав тождественные преобразования:
Из свойств прямолинейной функции известно, что угол наклона прямой в графике зависит от коэффициента при х, а второе слагаемое лишь сдвигает прямую в сторону параллельным переносом. Анализируя наш набор зависимостей, видим, что коэффициенты при х равны, а значит и прямые их графиков имеют одинаковый угол наклона. При этом слагаемые уравнений разные по значению, то есть графики сдвинуты относительно друг друга. Иными словами, прямые параллельны и не пересекаются, значит, данная система уравнений не имеет верных корней.
http://wika.tutoronline.ru/algebra/class/9/kak-reshat-sistemy-uravnenij-s-dvumya-peremennymi
http://urokimatematiki.ru/urok-sistema-lineynih-uravneniy-graficheskoe-reshenie-sistemi-477.html