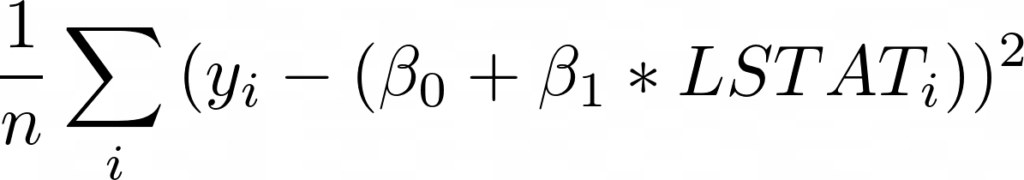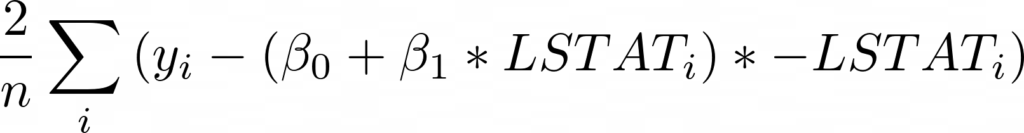Графическое изображение уравнения линейной регрессии это

Основы линейной регрессии

Что такое регрессия?

Разместим точки на двумерном графике рассеяния и скажем, что мы имеем линейное соотношение, если данные аппроксимируются прямой линией.

Если мы полагаем, что y зависит от x, причём изменения в y вызываются именно изменениями в x, мы можем определить линию регрессии (регрессия y на x), которая лучше всего описывает прямолинейное соотношение между этими двумя переменными.

Статистическое использование слова «регрессия» исходит из явления, известного как регрессия к среднему, приписываемого сэру Френсису Гальтону (1889).

Он показал, что, хотя высокие отцы имеют тенденцию иметь высоких сыновей, средний рост сыновей меньше, чем у их высоких отцов. Средний рост сыновей «регрессировал» и «двигался вспять» к среднему росту всех отцов в популяции. Таким образом, в среднем высокие отцы имеют более низких (но всё-таки высоких) сыновей, а низкие отцы имеют сыновей более высоких (но всё-таки довольно низких).

Линия регрессии

Математическое уравнение, которое оценивает линию простой (парной) линейной регрессии:

x называется независимой переменной или предиктором.

Y – зависимая переменная или переменная отклика. Это значение, которое мы ожидаем для y (в среднем), если мы знаем величину x, т.е. это «предсказанное значение y»

• a – свободный член (пересечение) линии оценки; это значение Y, когда x=0 (Рис.1).
• b – угловой коэффициент или градиент оценённой линии; она представляет собой величину, на которую Y увеличивается в среднем, если мы увеличиваем x на одну единицу.
• a и b называют коэффициентами регрессии оценённой линии, хотя этот термин часто используют только для b.

Парную линейную регрессию можно расширить, включив в нее более одной независимой переменной; в этом случае она известна как множественная регрессия.

Рис.1. Линия линейной регрессии, показывающая пересечение a и угловой коэффициент b (величину возрастания Y при увеличении x на одну единицу)

Метод наименьших квадратов

Мы выполняем регрессионный анализ, используя выборку наблюдений, где a и b – выборочные оценки истинных (генеральных) параметров, α и β , которые определяют линию линейной регрессии в популяции (генеральной совокупности).

Наиболее простым методом определения коэффициентов a и b является метод наименьших квадратов (МНК).

Подгонка оценивается, рассматривая остатки (вертикальное расстояние каждой точки от линии, например, остаток = наблюдаемому y – предсказанный y, Рис. 2).

Линию лучшей подгонки выбирают так, чтобы сумма квадратов остатков была минимальной.

Рис. 2. Линия линейной регрессии с изображенными остатками (вертикальные пунктирные линии) для каждой точки.

Предположения линейной регрессии

Итак, для каждой наблюдаемой величины остаток равен разнице и соответствующего предсказанного Каждый остаток может быть положительным или отрицательным.

Можно использовать остатки для проверки следующих предположений, лежащих в основе линейной регрессии:

• Между и существует линейное соотношение: для любых пар данные должны аппроксимировать прямую линию. Если нанести на двумерный график остатки, то мы должны наблюдать случайное рассеяние точек, а не какую-либо систематическую картину.

• Остатки нормально распределены с нулевым средним значением;

• Остатки имеют одну и ту же вариабельность (постоянную дисперсию) для всех предсказанных величин Если нанести остатки против предсказанных величин от мы должны наблюдать случайное рассеяние точек. Если график рассеяния остатков увеличивается или уменьшается с увеличением то это допущение не выполняется;

Если допущения линейности, нормальности и/или постоянной дисперсии сомнительны, мы можем преобразовать или и рассчитать новую линию регрессии, для которой эти допущения удовлетворяются (например, использовать логарифмическое преобразование или др.).

Аномальные значения (выбросы) и точки влияния

«Влиятельное» наблюдение, если оно опущено, изменяет одну или больше оценок параметров модели (т.е. угловой коэффициент или свободный член).

Выброс (наблюдение, которое противоречит большинству значений в наборе данных) может быть «влиятельным» наблюдением и может хорошо обнаруживаться визуально, при осмотре двумерной диаграммы рассеяния или графика остатков.

И для выбросов, и для «влиятельных» наблюдений (точек) используют модели, как с их включением, так и без них, обращают внимание на изменение оценки (коэффициентов регрессии).

При проведении анализа не стоит отбрасывать выбросы или точки влияния автоматически, поскольку простое игнорирование может повлиять на полученные результаты. Всегда изучайте причины появления этих выбросов и анализируйте их.

Гипотеза линейной регрессии

При построении линейной регрессии проверяется нулевая гипотеза о том, что генеральный угловой коэффициент линии регрессии β равен нулю.

Если угловой коэффициент линии равен нулю, между и нет линейного соотношения: изменение не влияет на

Для тестирования нулевой гипотезы о том, что истинный угловой коэффициент равен нулю можно воспользоваться следующим алгоритмом:

Вычислить статистику критерия, равную отношению , которая подчиняется распределению с степенями свободы, где стандартная ошибка коэффициента

,

— оценка дисперсии остатков.

Обычно если достигнутый уровень значимости нулевая гипотеза отклоняется.

Можно рассчитать 95% доверительный интервал для генерального углового коэффициента :

где процентная точка распределения со степенями свободы что дает вероятность двустороннего критерия

Это тот интервал, который содержит генеральный угловой коэффициент с вероятностью 95%.

Для больших выборок, скажем, мы можем аппроксимировать значением 1,96 (то есть статистика критерия будет стремиться к нормальному распределению)

Оценка качества линейной регрессии: коэффициент детерминации R 2

Из-за линейного соотношения и мы ожидаем, что изменяется, по мере того как изменяется , и называем это вариацией, которая обусловлена или объясняется регрессией. Остаточная вариация должна быть как можно меньше.

Если это так, то большая часть вариации будет объясняться регрессией, а точки будут лежать близко к линии регрессии, т.е. линия хорошо соответствует данным.

Долю общей дисперсии , которая объясняется регрессией называют коэффициентом детерминации, обычно выражают через процентное соотношение и обозначают R 2 (в парной линейной регрессии это величина r 2 , квадрат коэффициента корреляции), позволяет субъективно оценить качество уравнения регрессии.

Разность представляет собой процент дисперсии который нельзя объяснить регрессией.

Нет формального теста для оценки мы вынуждены положиться на субъективное суждение, чтобы определить качество подгонки линии регрессии.

Применение линии регрессии для прогноза

Можно применять регрессионную линию для прогнозирования значения по значению в пределе наблюдаемого диапазона (никогда не экстраполируйте вне этих пределов).

Мы предсказываем среднюю величину для наблюдаемых, которые имеют определенное значение путем подстановки этого значения в уравнение линии регрессии.

Итак, если прогнозируем как Используем эту предсказанную величину и ее стандартную ошибку, чтобы оценить доверительный интервал для истинной средней величины в популяции.

Повторение этой процедуры для различных величин позволяет построить доверительные границы для этой линии. Это полоса или область, которая содержит истинную линию, например, с 95% доверительной вероятностью.

Подобным образом можно рассчитать более широкую область, внутри которой, как мы ожидаем, лежит наибольшее число (обычно 95%) наблюдений.

Простые регрессионные планы

Простые регрессионные планы содержат один непрерывный предиктор. Если существует 3 наблюдения со значениями предиктора P , например, 7, 4 и 9, а план включает эффект первого порядка P , то матрица плана X будет иметь вид

а регрессионное уравнение с использованием P для X1 выглядит как

Если простой регрессионный план содержит эффект высшего порядка для P , например квадратичный эффект, то значения в столбце X1 в матрице плана будут возведены во вторую степень:

а уравнение примет вид

Y = b 0 + b 1 P 2

Сигма -ограниченные и сверхпараметризованные методы кодирования не применяются по отношению к простым регрессионным планам и другим планам, содержащим только непрерывные предикторы (поскольку, просто не существует категориальных предикторов). Независимо от выбранного метода кодирования, значения непрерывных переменных увеличиваются в соответствующей степени и используются как значения для переменных X . При этом перекодировка не выполняется. Кроме того, при описании регрессионных планов можно опустить рассмотрение матрицы плана X , а работать только с регрессионным уравнением.

Пример: простой регрессионный анализ

Этот пример использует данные, представленные в таблице:

Рис. 3. Таблица исходных данных.

Данные составлены на основе сравнения переписей 1960 и 1970 в произвольно выбранных 30 округах. Названия округов представлены в виде имен наблюдений. Информация относительно каждой переменной представлена ниже:

Рис. 4. Таблица спецификаций переменных.

Задача исследования

Для этого примера будут анализироваться корреляция уровня бедности и степень, которая предсказывает процент семей, которые находятся за чертой бедности. Следовательно мы будем трактовать переменную 3 ( Pt_Poor ) как зависимую переменную.

Можно выдвинуть гипотезу: изменение численности населения и процент семей, которые находятся за чертой бедности, связаны между собой. Кажется разумным ожидать, что бедность ведет к оттоку населения, следовательно, здесь будет отрицательная корреляция между процентом людей за чертой бедности и изменением численности населения. Следовательно мы будем трактовать переменную 1 ( Pop_Chng ) как переменную-предиктор.

Просмотр результатов

Коэффициенты регрессии

Рис. 5. Коэффициенты регрессии Pt_Poor на Pop_Chng.

На пересечении строки Pop_Chng и столбца Парам. не стандартизованный коэффициент для регрессии Pt_Poor на Pop_Chng равен -0.40374 . Это означает, что для каждого уменьшения численности населения на единицу, имеется увеличение уровня бедности на .40374. Верхний и нижний (по умолчанию) 95% доверительные пределы для этого не стандартизованного коэффициента не включают ноль, так что коэффициент регрессии значим на уровне p . Обратите внимание на не стандартизованный коэффициент, который также является коэффициентом корреляции Пирсона для простых регрессионных планов, равен -.65, который означает, что для каждого уменьшения стандартного отклонения численности населения происходит увеличение стандартного отклонения уровня бедности на .65.

Распределение переменных

Коэффициенты корреляции могут стать существенно завышены или занижены, если в данных присутствуют большие выбросы. Изучим распределение зависимой переменной Pt_Poor по округам. Для этого построим гистограмму переменной Pt_Poor .

Рис. 6. Гистограмма переменной Pt_Poor.

Как вы можете заметить, распределение этой переменной заметно отличается от нормального распределения. Тем не менее, хотя даже два округа (два правых столбца) имеют высокий процент семей, которые находятся за чертой бедности, чем ожидалось в случае нормального распределения, кажется, что они находятся «внутри диапазона.»

Рис. 7. Гистограмма переменной Pt_Poor.

Это суждение в некоторой степени субъективно. Эмпирическое правило гласит, что выбросы необходимо учитывать, если наблюдение (или наблюдения) не попадают в интервал (среднее ± 3 умноженное на стандартное отклонение). В этом случае стоит повторить анализ с выбросами и без, чтобы убедиться, что они не оказывают серьезного эффекта на корреляцию между членами совокупности.

Диаграмма рассеяния

Если одна из гипотез априори о взаимосвязи между заданными переменными, то ее полезно проверить на графике соответствующей диаграммы рассеяния.

Рис. 8. Диаграмма рассеяния.

Диаграмма рассеяния показывает явную отрицательную корреляцию ( -.65 ) между двумя переменными. На ней также показан 95% доверительный интервал для линии регрессии, т.е., с 95% вероятностью линия регрессии проходит между двумя пунктирными кривыми.

Критерии значимости

Рис. 9. Таблица, содержащая критерии значимости.

Критерий для коэффициента регрессии Pop_Chng подтверждает, что Pop_Chng сильно связано с Pt_Poor , p .

На этом примере было показано, как проанализировать простой регрессионный план. Была также представлена интерпретация не стандартизованных и стандартизованных коэффициентов регрессии. Обсуждена важность изучения распределения откликов зависимой переменной, продемонстрирована техника определения направления и силы взаимосвязи между предиктором и зависимой переменной.

Простая линейная регрессия

В предыдущих заметках предметом анализа часто становилась отдельная числовая переменная, например, доходность взаимных фондов, время загрузки Web-страницы или объем потребления безалкогольных напитков. В настоящей и следующих заметках мы рассмотрим методы предсказания значений числовой переменной в зависимости от значений одной или нескольких других числовых переменных. [1]

Материал будет проиллюстрирован сквозным примером. Прогнозирование объема продаж в магазине одежды. Сеть магазинов уцененной одежды Sunflowers на протяжении 25 лет постоянно расширялась. Однако в настоящее время у компании нет систематического подхода к выбору новых торговых точек. Место, в котором компания собирается открыть новый магазин, определяется на основе субъективных соображений. Критериями выбора являются выгодные условия аренды или представления менеджера об идеальном местоположении магазина. Представьте, что вы — руководитель отдела специальных проектов и планирования. Вам поручили разработать стратегический план открытия новых магазинов. Этот план должен содержать прогноз годового объема продаж во вновь открываемых магазинах. Вы полагаете, что торговая площадь непосредственно связана с объемом выручки, и хотите учесть этот факт в процессе принятия решения. Как разработать статистическую модель, позволяющую прогнозировать годовой объем продаж на основе размера нового магазина?

Как правило, для предсказания значений переменной используется регрессионный анализ. Его цель — разработать статистическую модель, позволяющую предсказывать значения зависимой переменной, или отклика, по значениям, по крайней мере одной, независимой, или объясняющей, переменной. В настоящей заметке мы рассмотрим простую линейную регрессию — статистический метод, позволяющий предсказывать значения зависимой переменной Y по значениям независимой переменной X. В последующих заметках будет описана модель множественной регрессии, предназначенная для предсказания значений независимой переменной Y по значениям нескольких зависимых переменных (Х₁, Х₂, …, X_k). [2]

Скачать заметку в формате Word или pdf, примеры в формате Excel2013

Виды регрессионных моделей

В заметке Представление числовых данных в виде таблиц и диаграмм для иллюстрации зависимости между переменными X и Y использовалась диаграмма разброса. На ней значения переменной X откладывались по горизонтальной оси, а значения переменной Y — по вертикальной. Зависимость между двумя переменными может быть разной: от самой простой до крайне сложной. Пример простейшей (линейной) зависимости показан на рис. 1.

Рис. 1. Положительная линейная зависимость

Простая линейная регрессия:

где β₀ — сдвиг (длина отрезка, отсекаемого на координатной оси прямой Y), β₁ — наклон прямой Y, ε_i— случайная ошибка переменной Y в i-м наблюдении.

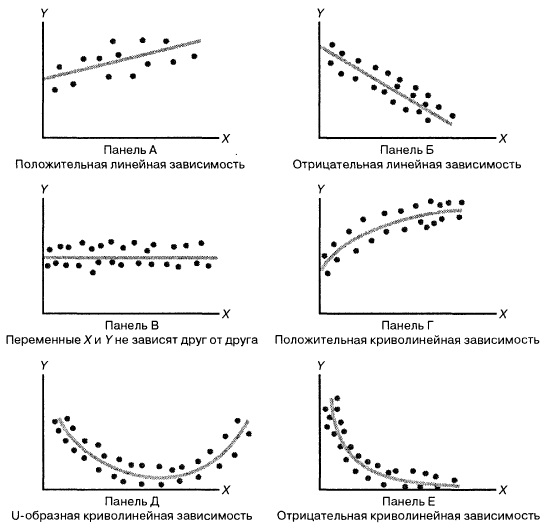
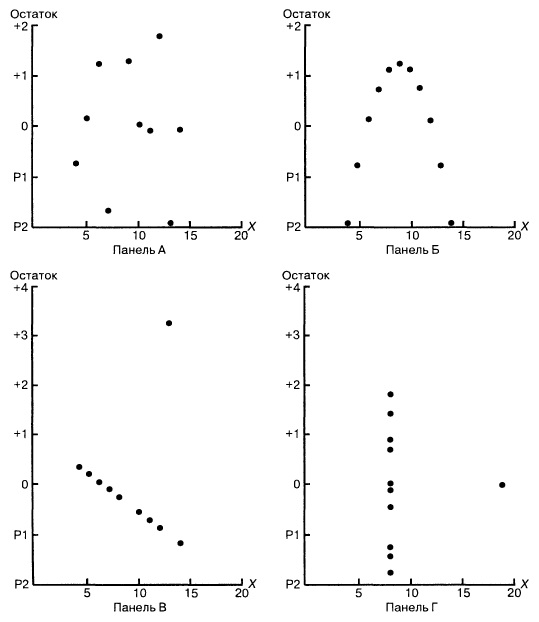
В этой модели наклон β₁ представляет собой количество единиц измерения переменной Y, приходящихся на одну единицу измерения переменной X. Эта величина характеризует среднюю величину изменения переменной Y (положительного или отрицательного) на заданном отрезке оси X. Сдвиг β₀ представляет собой среднее значение переменной Y, когда переменная X равна 0. Последний компонент модели ε_i является случайной ошибкой переменной Y в i-м наблюдении. Выбор подходящей математической модели зависит от распределения значений переменных X и Y на диаграмме разброса. Различные виды зависимости переменных показаны на рис. 2.

Рис. 2. Диаграммы разброса, иллюстрирующие разные виды зависимостей

На панели А значения переменной Y почти линейно возрастают с увеличением переменной X. Этот рисунок аналогичен рис. 1, иллюстрирующему положительную зависимость между размером магазина (в квадратных футах) и годовым объемом продаж. Панель Б является примером отрицательной линейной зависимости. Если переменная X возрастает, переменная Y в целом убывает. Примером этой зависимости является связь между стоимостью конкретного товара и объемом продаж. На панели В показан набор данных, в котором переменные X и Y практически не зависят друг от друга. Каждому значению переменной X соответствуют как большие, так и малые значения переменной Y. Данные, приведенные на панели Г, демонстрируют криволинейную зависимость между переменными X и Y. Значения переменной Y возрастают при увеличении переменной X, однако скорость роста после определенных значений переменной X падает. Примером положительной криволинейной зависимости является связь между возрастом и стоимостью обслуживания автомобилей. По мере старения машины стоимость ее обслуживания сначала резко возрастает, однако после определенного уровня стабилизируется. Панель Д демонстрирует параболическую U-образную форму зависимости между переменными X и Y. По мере увеличения значений переменной X значения переменной Y сначала убывают, а затем возрастают. Примером такой зависимости является связь между количеством ошибок, совершенных за час работы, и количеством отработанных часов. Сначала работник осваивается и делает много ошибок, потом привыкает, и количество ошибок уменьшается, однако после определенного момента он начинает чувствовать усталость, и число ошибок увеличивается. На панели Е показана экспоненциальная зависимость между переменными X и Y. В этом случае переменная Y сначала очень быстро убывает при возрастании переменной X, однако скорость этого убывания постепенно падает. Например, стоимость автомобиля при перепродаже экспоненциально зависит от его возраста. Если перепродавать автомобиль в течение первого года, его цена резко падает, однако впоследствии ее падение постепенно замедляется.

Мы кратко рассмотрели основные модели, которые позволяют формализовать зависимости между двумя переменными. Несмотря на то что диаграмма разброса чрезвычайно полезна при выборе математической модели зависимости, существуют более сложные и точные статистические процедуры, позволяющие описать отношения между переменными. В дальнейшем мы будем рассматривать лишь линейную зависимость.

Вывод уравнения простой линейной регрессии

Вернемся к сценарию, изложенному в начале главы. Наша цель — предсказать объем годовых продаж для всех новых магазинов, зная их размеры. Для оценки зависимости между размером магазина (в квадратных футах) и объемом его годовых продаж создадим выборки из 14 магазинов (рис. 3).

Рис. 3. Площади и годовые объемы продаж 14 магазинов сети Sunflowers: (а) исходные данные; (б) диаграмма разброса

Анализ рис. 3 показывает, что между площадью магазина X и годовым объемом продаж Y существует положительная зависимость. Если площадь магазина увеличивается, объем продаж возрастает почти линейно. Таким образом, наиболее подходящей для исследования является линейная модель. Остается лишь определить, какая из линейных моделей точнее остальных описывает зависимость между анализируемыми переменными.

Метод наименьших квадратов

Данные, представленные на рис. 1а, получены для случайной выборки магазинов. Если верны некоторые предположения (об этом чуть позже), в качестве оценки параметров генеральной совокупности (β₀ и β₁) можно использовать сдвиг b₀ и наклон b₁ прямой Y. Таким образом, уравнение простой линейной регрессии принимает следующий вид:

где — предсказанное значение переменной Y для i-гo наблюдения, X_i — значение переменной X в i-м наблюдении.

Для того чтобы предсказать значение переменной Y, в уравнении (2) необходимо определить два коэффициента регрессии — сдвиг b₀ и наклон b₁ прямой Y. Вычислив эти параметры, проведем прямую на диаграмме разброса. Затем исследователь может визуально оценить, насколько близка регрессионная прямая к точкам наблюдения. Простая линейная регрессия позволяет найти прямую линию, максимально приближенную к точкам наблюдения. Критерии соответствия можно задать разными способами. Возможно, проще всего минимизировать разности между фактическими значениями Y_i, и предсказанными значениями . Однако, поскольку эти разности могут быть как положительными, так и отрицательными, следует минимизировать сумму их квадратов.

Поскольку = b₀ + b₁X_i, сумма квадратов принимает следующий вид:

Параметры b₀ и b₁ неизвестны. Таким образом, сумма квадратов разностей является функцией, зависящей от сдвига b₀ и наклона b₁ выборки Y. Для того чтобы найти значения параметров b₀ и b₁, минимизирующих сумму квадратов разностей, применяется метод наименьших квадратов. При любых других значениях сдвига b₀ и наклона b₁ сумма квадратов разностей между фактическими значениями переменной Y и ее наблюдаемыми значениями лишь увеличится.

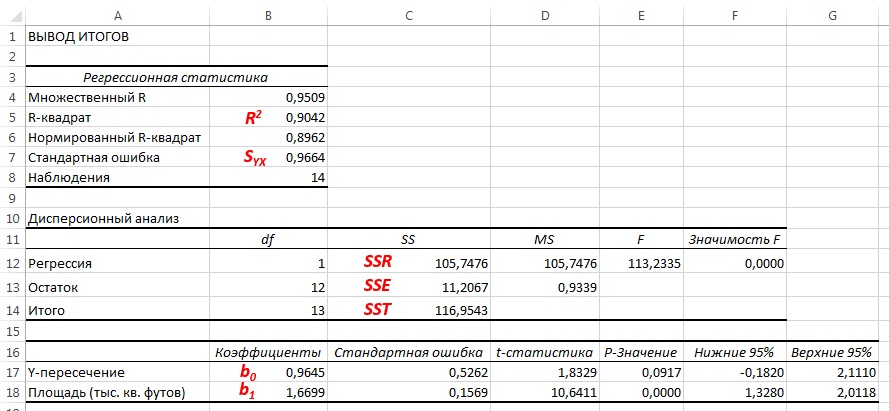
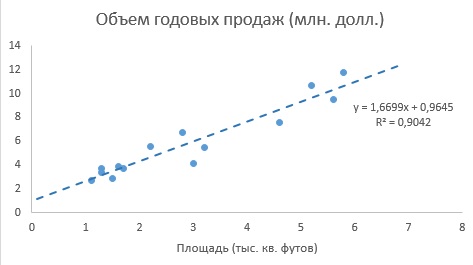
До того, как Excel взял на себя всю рутинную работу, вычисления по методу наименьших квадратов были очень трудоемкими. Excel позволяет решать подобные задачи двумя способами. Во-первых, можно воспользоваться Пакетом анализа (строка Регрессия). Результаты представлены на рис. 4. Во-вторых, можно, выделив точки на графике (как на рис. 3б), кликнуть правой кнопкой мыши и выбрать Добавить линию тренда. Далее можно выбрать вид линии тренда (в нашем случае – Линейная), отформатировать линию, показать на графике уравнение и величину достоверности аппроксимации (R 2 ) (рис. 5).

Рис. 4. Результаты решения задачи о зависимости между площадями и годовыми объемами продаж в магазинах сети Sunflower (получены с помощью Пакета анализа Excel)

Рис. 5. Диаграмма разброса и линия регрессии (тренда) в задаче о выборе магазина

Как следует из рис. 4 и 5, b₀ = 0,9645, а b₁ = 1,6699. Таким образом, уравнение линейной регрессии для этих данных имеет следующий вид: = 0,9645 + 1,6699X_i. Вычисленный наклон b₁ = +1,6699. Это означает, что при возрастании переменной X на единицу среднее значение переменной Y возрастает на 1,6699 единиц. Иначе говоря, увеличение площади магазина на один квадратный фут приводит к увеличению годового объема продаж на 1,67 тыс. долл. Таким образом, наклон представляет собой долю годового объема продаж, зависящую от размера магазина. Вычисленный сдвиг b₀ = +0,9645 (млн. долл.). Эта величина представляет собой среднее значение переменной Y при X = 0. Поскольку площадь магазина не может равняться нулю, сдвиг можно считать долей годового дохода, зависящей от других факторов. Следует отметить, однако, что сдвиг переменной Y выходит за пределы диапазона переменной X. Следовательно, к интерпретации параметра b₀ необходимо относиться внимательно.

Пример 1. Один экономист решил предсказать изменение индекса 500 наиболее активно покупаемых акций на Нью-Йоркской фондовой бирже, публикуемого агентством Standard and Poor, на основе показателей экономики США за 50 лет. В результате он получил следующее уравнение линейной регрессии: Ŷ_i = –5,0 + 7Х_i. Какой смысл имеют параметры сдвига b₀ и наклона b₁.

Решение. Сдвиг регрессии b₀ равен –5,0. Это значит, что если рост экономики США равен нулю, индекс акций за год снизится на 5%. Наклон b₁ равен 7. Следовательно, при увеличении темпов роста экономики на 1% индекс акций возрастает на 7%.

Пример 2. Вернемся к сценарию, изложенному в начале заметки. Применим модель линейной регрессии для прогноза объема годовых продаж во всех новых магазинах в зависимости от их размеров. Предположим, что площадь магазина равна 4000 квадратных футов. Какой среднегодовой объем продаж можно прогнозировать?

Решение. Подставим значение X = 4 (тыс. кв. футов) в уравнение линейной регрессии: = 0,9645 + 1,6699X_i = 0,9645 + 1,6699*4 = 7,644 млн. долл. Итак, прогнозируемый среднегодовой объем продаж в магазине, площадь которого равна 4000 кв. футов, составляет 7 644 000 долл.

Прогнозирование в регрессионном анализе: интерполяция и экстраполяция

Применяя регрессионную модель для прогнозирования, необходимо учитывать лишь допустимые значения независимой переменной. В этот диапазон входят все значения переменной X, начиная с минимальной и заканчивая максимальной. Таким образом, предсказывая значение переменной Y при конкретном значении переменной X, исследователь выполняет интерполяцию между значениями переменной X в диапазоне возможных значений. Однако экстраполяция значений за пределы этого интервала не всегда релевантна. Например, пытаясь предсказать среднегодовой объем продаж в магазине, зная его площадь (рис. 3а), мы можем вычислять значение переменной Y лишь для значений X от 1,1 до 5,8 тыс. кв. футов. Следовательно, прогнозировать среднегодовой объем продаж можно лишь для магазинов, площадь которых не выходит за пределы указанного диапазона. Любая попытка экстраполяции означает, что мы предполагаем, будто линейная регрессия сохраняет свой характер за пределами допустимого диапазона.

Оценки изменчивости

Вычисление сумм квадратов. Для того чтобы предсказать значение зависимой переменной по значениям независимой переменной в рамках избранной статистической модели, необходимо оценить изменчивость. Существует несколько способов оценки изменчивости. Первый способ использует общую сумму квадратов (total sum of squares — SST), позволяющую оценить колебания значений Y_i вокруг среднего значения . В регрессионном анализе полная вариация, представляющая собой полную сумму квадратов, разделяется на объяснимую вариацию, или сумму квадратов регрессии (regression sum of squares — SSR), и необъяснимую вариацию, или сумму квадратов ошибок (error sum of squares — SSE). Объяснимая вариация характеризует взаимосвязь между переменными X и Y, а необъяснимая зависит от других факторов (рис. 6).

Рис. 6. Оценки изменчивости в модели регрессии

Сумма квадратов регрессии (SSR) представляет собой сумму квадратов разностей между Ŷ_i (предсказанным значением переменной Y) и (средним значением переменной Y). Сумма квадратов ошибок (SSE) является частью вариации переменной Y, которую невозможно описать с помощью регрессионной модели. Эта величина зависит от разностей между наблюдаемыми и предсказанными значениями.

Полная сумма квадратов (SST) равна сумме квадратов регрессии плюс сумма квадратов ошибок:

(3) SST = SSR + SSE

Полная сумма квадратов (SST) равна сумме квадратов разностей между наблюдаемыми значениями переменной Y и ее средним значением:

Сумма квадратов регрессии (SSR) равна сумме квадратов разностей между предсказанными значениями переменной Y и ее средним значением:

Сумма квадратов ошибок (SSE) равна сумме квадратов разностей между наблюдаемыми и предсказанными значениями переменной Y:

Суммы квадратов, вычисленные с помощью программы Пакета анализа Excel при решении задачи о сети магазинов Sunflowers, представлены на рис. 4.

Полная сумма квадратов разностей равна SST = 116,9543. Эта величина состоит из суммы квадратов регрессии (SSR) равной 105,7476, и суммы квадратов ошибок (SSE), равной 11,2067.

Коэффициент смешанной корреляции. Величины SSR, SSE и SST не имеют очевидной интерпретации. Однако отношение суммы квадратов регрессии (SSR) к полной сумме квадратов (SST) представляет собой оценку полезности регрессионного уравнения. Это отношение называется коэффициентом смешанной корреляции r 2 :

Коэффициент смешанной корреляции оценивает долю вариации переменной Y, которая объясняется независимой переменной X в регрессионной модели. В задаче о сети магазинов Sunflowers SSR = 105,7476 и SST = 116,9543. Следовательно, r 2 = 105,7476 / 116,9543 = 0,904. Таким образом, 90,4% вариации годового объема продаж объясняется изменчивостью площади магазинов, измеренной в квадратных футах. Данная величина r 2 свидетельствует о сильной положительной линейной взаимосвязи между двумя переменными, поскольку применение регрессионной модели снижает изменчивость прогнозируемых годовых объемов продаж на 90,4%. Только 9,6% изменчивости годовых объемов продаж в выборке магазинов объясняются другими факторами, не учтенными в регрессионной модели.

Коэффициент смешанной корреляции в задаче о сети магазинов Sunflowers представлен в таблице Регрессионная статистика на рис. 4.

Среднеквадратичная ошибка оценки. Хотя метод наименьших квадратов позволяет вычислить линию, минимизирующую отклонение от наблюдаемых значений, наличие суммы квадратов ошибок (SSE) свидетельствует о том, что линейная регрессия не дает абсолютной точности прогноза, если, конечно, точки наблюдения не лежат на регрессионной прямой. Однако ожидать этого так же неестественно, как предполагать, что все выборочные значения точно равны их среднему арифметическому. Следовательно, необходима статистика, которая позволила бы оценить отклонение предсказанных значений переменной Y от ее реальных значений, аналогично тому, как стандартное отклонение, введенное ранее, позволяет оценить колебание данных вокруг их средней величины. Стандартное отклонение наблюдаемых значений переменной Y от ее регрессионной прямой называется среднеквадратичной ошибкой оценки. Отклонение реальных данных от регрессионной прямой в задаче о сети магазинов Sunflowers показано на рис. 5.

Среднеквадратичная ошибка оценки

где Y_i — фактическое значение переменной Y при заданном значении X_i, Ŷ_i — предсказанное значение переменной Y при заданном значении X_i, SSE — сумма квадратов ошибок.

Поскольку SSE = 11,2067, по формуле (8) получаем:

Таким образом, среднеквадратичная ошибка оценки равна 0,9664 млн. долл. (т.е. 966 400 долл.). Этот параметр также рассчитывается Пакетом анализа (см. рис. 4). Среднеквадратичная ошибка оценки характеризует отклонение реальных данных от линии регрессии. Она измеряется в тех же единицах, что и переменная Y. По смыслу среднеквадратичная ошибка очень похожа на стандартное отклонение. В то время как стандартное отклонение характеризует разброс данных вокруг их среднего значения, среднеквадратичная ошибка позволяет оценить колебание точек наблюдения вокруг регрессионной прямой. Cреднеквадратичная ошибка оценки позволяет обнаружить статистически значимую зависимость, существующую между двумя переменными, и предсказать значения переменной Y.

Предположения

Обсуждая методы проверки гипотез и дисперсионного анализа, мы не раз подчеркивали важность условий, которые должны обеспечивать корректность сделанных выводов. Поскольку и регрессионный, и дисперсионный анализ используют линейную модель, условия их применения приблизительно одинаковы:

• Ошибка должна иметь нормальное распределение.
• Вариация данных вокруг линии регрессии должна быть постоянной.
• Ошибки должны быть независимыми.

Первое предположение, о нормальном распределении ошибок, требует, чтобы при каждом значении переменной X ошибки линейной регрессии имели нормальное распределение (рис. 7). Как и t— и F-критерий дисперсионного анализа, регрессионный анализ довольно устойчив к нарушениям этого условия. Если распределение ошибок относительно линии регрессии при каждом значении X не слишком сильно отличается от нормального, выводы относительно линии регрессии и коэффициентов регрессии изменяются незначительно.

Рис. 7. Предположение о нормальном распределении ошибок

Второе условие заключается в том, что вариация данных вокруг линии регрессии должна быть постоянной при любом значении переменной X. Это означает, что величина ошибки как при малых, так и при больших значениях переменной X должна изменяться в одном и том же интервале (см. рис. 7). Это свойство очень важно для метода наименьших квадратов, с помощью которого определяются коэффициенты регрессии. Если это условие нарушается, следует применять либо преобразование данных, либо метод наименьших квадратов с весами.

Третье предположение, о независимости ошибок, заключается в том, что ошибки регрессии не должны зависеть от значения переменной X. Это условие особенно важно, если данные собираются на протяжении определенного отрезка времени. В этих ситуациях ошибки, присущие конкретному отрезку времени, часто коррелируют с ошибками, характерными для предыдущего периода.

Анализ остатков

Чуть выше при решении задачи о сети магазинов Sunflowers мы использовали модель линейной регрессии. Рассмотрим теперь анализ ошибок — графический метод, позволяющий оценить точность регрессионной модели. Кроме того, с его помощью можно обнаружить потенциальные нарушения условий применения регрессионного анализа.

Оценка пригодности эмпирической модели. Остаток, или оценка ошибки е_i, представляет собой разность между наблюдаемым (Y_i) и предсказанным (Ŷ_i) значениями зависимой переменной при заданном значении X_i.

Для оценки пригодности эмпирической модели регрессии остатки откладываются по вертикальной оси, а значения X_i — по горизонтальной. Если эмпирическая модель пригодна, график не должен иметь ярко выраженной закономерности. Если же модель регрессии не пригодна, на рисунке проявится зависимость между значениями X_i и остатками е_i.

Рассмотрим примеры (рис. 8). Панель А иллюстрирует возрастание переменной Y при увеличении переменной X. Однако зависимость между этими переменными носит нелинейный характер, поскольку скорость возрастания переменной Y падает при увеличении переменной X. Таким образом, для аппроксимации зависимости между этими переменными лучше подойдет квадратичная модель. Особенно ярко квадратичная зависимость между величинами X_i и e_i проявляется на панели Б. Графическое изображение остатков позволяет отфильтровать или удалить линейную зависимость между переменными X и Y и выявить недостаточную точность модели простой линейной регрессии. Таким образом, в данной ситуации вместо простой линейной модели должна применяться квадратичная модель, обладающая более высокой точностью.

Рис. 8. Исследование эмпирической модели простой линейной регрессии

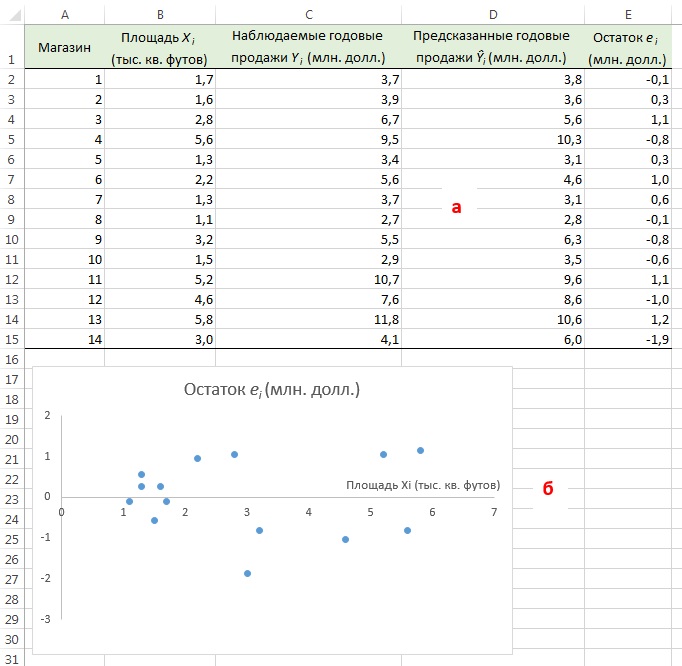
Вернемся к задаче о сети магазинов Sunflowers и посмотрим, хорошо ли подходит простая линейная регрессия для ее решения. Соответствующие данные и расчеты приведены на рис. 9а (формулы можно посмотреть в Excel-файле). Построим диаграмму разброса, откладывая по вертикальной оси остатки e_i, а по горизонтальной — независимую переменную X_i (рис. 9б). Несмотря на большой разброс остатков, между e_i и Х_i нет ярко выраженной зависимости. Остатки одинаково часто принимают как положительные, так и отрицательные значения. Это позволяет сделать вывод, что модель линейной регрессии пригодна для решения задачи о сети магазинов Sunflowers.

Рис. 9. Остатки e_i, вычисленные при решении задачи о сети магазинов Sunflowers

Значения остатков (таблица на рис. 9а) и график остатков (аналог рис. 9б) можно получить непосредственно в процедуре Регрессия Пакета анализа. Просто поставьте соответствующие галки (рис. 10).

Рис. 10. Остатки e_i и график остатков полученные с помощью Пакета анализа

Проверка условий. График остатков позволяет оценить вариации ошибок. На рис. 10 нет особых различий между ошибками, соответствующими разным значениям X_i. Следовательно, вариации ошибок при разных значениях Х_i приблизительно одинаковы. Рассмотрим гипотетическую ситуацию, в которой это условие не выполняется (рис. 11). На этом рисунке изображен эффект веера: при возрастании значений Х_i ошибки увеличиваются. Таким образом, изменчивость значений Y_i при разных значениях Х_i является непостоянной.

Рис. 11. Пример нарушения условия независимости вариаций ошибок от X_i

Нормальность. Чтобы проверить предположение о нормальном распределении ошибок, построим график нормального распределения на основе точечного графика, на вертикальной оси которого отложены значения остатков, а на горизонтальной оси — соответствующие квантили стандартизованного нормального распределения (подробнее см. Проверка гипотезы о нормальном распределении). Для построения такого графика значения остатков должны быть упорядочены по возрастанию (рис. 12). График нормального распределения может быть построен одним кликом с помощью Пакета анализа Excel – просто поставьте соответствующую галочку в окне Регрессия (см. рис. 10, самый низ окна Регрессия – опция График нормальной вероятности).

Рис. 12. График нормального распределения для остатков

Без визуализации данных (с помощью гистограммы, диаграммы «ствол и листья», блочной диаграммы или графика как на рис. 12) проверить предположение о нормальном распределении ошибок очень трудно. Данные, изображенные на рис. 12, не слишком сильно отличаются от нормального распределения. Устойчивость регрессионного анализа и небольшой объем выборки позволяют утверждать, что условие о нормальном распределении ошибок нарушается незначительно.

Независимость. Предположение о независимости ошибок также проверяется с помощью графика остатков. Данные, собранные на протяжении некоторого периода времени, иногда демонстрируют эффект автокорреляции между последовательными наблюдениями. В таких ситуациях остатки зависят от значений предыдущих остатков. Подобная связь между остатками нарушает предположение о независимости ошибок. Эффект автокорреляции хорошо выявляется на графике. Кроме того, его можно измерить с помощью процедуры Дурбина-Уотсона (см. ниже). Если данные о размерах магазинов и объемах продаж собирались в течение одного и того же периода времени, гипотезу об их независимости проверять не имеет смысла.

Измерение автокорреляции: статистика Дурбина–Уотсона

Одним из основных предположений о регрессионной модели является гипотеза о независимости ее ошибок. Если данные собираются в течение определенного отрезка времени, это условие часто нарушается, поскольку остаток в определенный момент времени может оказаться приблизительно равным предыдущим остаткам. Такое поведение остатков называется автокорреляцией. Если набор данных обладает свойством автокорреляции, корректность регрессионной модели становится весьма сомнительной.

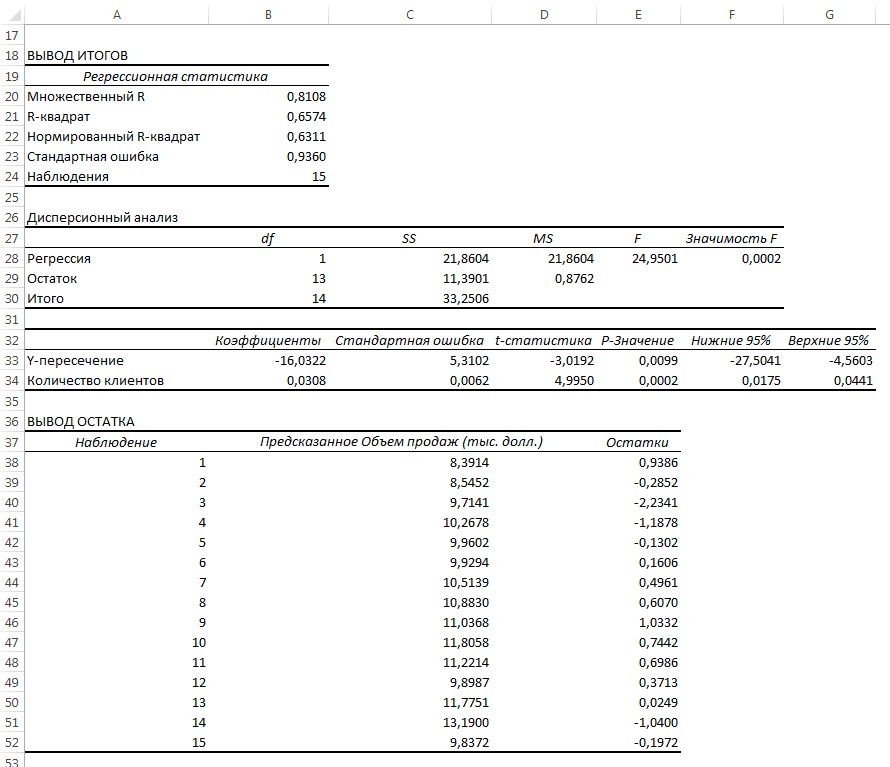
Распознавание автокорреляции с помощью графика остатков. Для выявления автокорреляции необходимо упорядочить остатки по времени и построить их график. Если данные обладают положительной автокорреляцией, на графике возникнут кластеры остатков, имеющие одинаковый знак. В случае отрицательной автокорреляции остатки будут скачкообразно принимать то положительные, то отрицательные значения. Этот вид автокорреляции очень редко встречается в регрессионном анализе, поэтому мы рассмотрим лишь положительную автокорреляцию. Проиллюстрируем ее следующим примером. Предположим, что менеджер магазина, доставляющего товары на дом, пытается предсказать объем продаж по количеству клиентов, совершивших покупки в течение 15 недель (рис. 13).

Рис. 13. Количество клиентов и объемы продаж за 15 недель

Поскольку данные собирались на протяжении 15 последовательных недель в одном и том же магазине, необходимо определить, наблюдается ли эффект автокорреляции. Построим регрессию с использованием Пакета анализа; включим вывод Остатков, но не будем включать График остатков (рис. 14).

Рис. 14. Параметры линейной регрессии, полученные с использованием Пакета анализа

Анализ рис. 14 показывает, что r 2 = 0,657. Это значит, что 65,7% вариации объемов продаж объясняется изменчивостью количества клиентов. Кроме того, сдвиг b₀ переменной Y равен –16,032, а наклон b₁ = 0,0308. Однако, прежде чем применять эту модель, необходимо выполнить анализ остатков. Поскольку данные собирались на протяжении 15 последовательных недель, их следует отобразить на графике в том же порядке (рис. 15).

Рис. 15. Зависимость остатков от времени

Анализ рис. 15 показывает, что остатки циклически колеблются вверх и вниз. Эта цикличность является явным признаком автокорреляции. Следовательно, гипотезу о независимости остатков следует отклонить.

Статистика Дурбина-Уотсона. Автокорреляцию можно выявить и измерить с помощью статистики Дурбина-Уотсона. Эта статистика оценивает корреляцию между соседними остатками:

где е_i — остаток, соответствующий i-му периоду времени.

Чтобы лучше понять статистику Дурбина-Уотсона, рассмотрим ее составные части. Числитель представляет собой сумму квадратов разностей между соседними остатками, начиная со второго и заканчивая n-м наблюдением. Знаменатель является суммой квадратов остатков. Вот, что по этому поводу написано в Википедии:

где ρ₁ – коэффициент автокорреляции; если ρ₁ = 0 (нет автокорреляции), D ≈ 2; если ρ₁ ≈ 1 (положительная автокорреляции), D ≈ 0; если ρ₁ = -1 (отрицательная автокорреляции), D ≈ 4.

На практике применение критерия Дурбина-Уотсона основано на сравнении величины D с критическими теоретическими значениями d_L и d_U для заданного числа наблюдений n, числа независимых переменных модели k (для простой линейной регрессии k = 1) и уровня значимости α. Если D d_U, гипотеза не отвергается (то есть автокорреляция отсутствует); если d_L t_U = 2,1788 (рис. 19), нулевая гипотеза Н₀ отклоняется. С другой стороны, р-значение для Х = 10,6411, вычисляемое по формуле =1-СТЬЮДЕНТ.РАСП(D3;12;ИСТИНА), приближенно равно нулю, поэтому гипотеза Н₀ снова отклоняется. Тот факт, что р-значение почти равно нулю, означает, что если бы между размерами магазинов и годовым объемом продаж не существовало реальной линейной зависимости, обнаружить ее с помощью линейной регрессии было бы практически невозможно. Следовательно, между средним годовым объемом продаж в магазинах и их размером существует статистически значимая линейная зависимость.

Рис. 19. Проверка гипотезы о наклоне генеральной совокупности при уровне значимости, равном 0,05, и 12 степенях свободы

Применение F-критерия для наклона. Альтернативным подходом к проверке гипотез о наклоне простой линейной регрессии является использование F-критерия. Напомним, что F-критерий применяется для проверки отношения между двумя дисперсиями (подробнее см. Однофакторный дисперсионный анализ). При проверке гипотезы о наклоне мерой случайных ошибок является дисперсия ошибки (сумма квадратов ошибок, деленная на количество степеней свободы), поэтому F-критерий использует отношение дисперсии, объясняемой регрессией (т.е. величины SSR, деленной на количество независимых переменных k), к дисперсии ошибок (MSE = S_YX 2 ).

По определению F-статистика равна среднему квадрату отклонений, обусловленных регрессией (MSR), деленному на дисперсию ошибки (MSE): F = MSR/MSE, где MSR = SSR / k, MSE = SSE/(n– k – 1), k – количество независимых переменных в регрессионной модели. Тестовая статистика F имеет F-распределение с k и n – k – 1 степенями свободы.

При заданном уровне значимости α решающее правило формулируется так: если F > F_U, нулевая гипотеза отклоняется; в противном случае она не отклоняется. Результаты, оформленные в виде сводной таблицы дисперсионного анализа, приведены на рис. 20.

Рис. 20. Таблица дисперсионного анализа для проверки гипотезы о статистической значимости коэффициента регрессии

Аналогично t-критерию F-критерий выводится в таблицу при использовании Пакета анализа (опция Регрессия). Полностью результаты работы Пакета анализа приведены на рис. 4, фрагмент, относящийся к F-статистике – на рис. 21.

Рис. 21. Результаты применения F-критерия, полученные с помощью Пакета анализа Excel

F-статистика равна 113,23, а р-значение близко к нулю (ячейка Значимость F). Если уровень значимости α равен 0,05, определить критическое значение F-распределения с одной и 12 степенями свободы можно по формуле F_U =F.ОБР(1-0,05;1;12) = 4,7472 (рис. 22). Поскольку F = 113,23 > F_U = 4,7472, причем р-значение близко к 0 0, r = –, если b₁ 2 = 0,904, а b₁— +1,670 (см. рис. 4). Поскольку b₁ > 0, коэффициент корреляции между объемом годовых продаж и размером магазина равен r = +√0,904 = +0,951. Проверим нулевую гипотезу, утверждающую, что между этими переменными нет корреляции, используя t-статистику:

При уровне значимости α = 0,05 нулевую гипотезу следует отклонить, поскольку t = 10,64 > 2,1788. Таким образом, можно утверждать, что между объемом годовых продаж и размером магазина существует статистически значимая связь.

При обсуждении выводов, касающихся наклона генеральной совокупности, доверительные интервалы и критерии для проверки гипотез являются взаимозаменяемыми инструментами. Однако вычисление доверительного интервала, содержащего коэффициент корреляции, оказывается более сложным делом, поскольку вид выборочного распределения статистики r зависит от истинного коэффициента корреляции.

Оценка математического ожидания и предсказание индивидуальных значений

В этом разделе рассматриваются методы оценки математического ожидания отклика Y и предсказания индивидуальных значений Y при заданных значениях переменной X.

Построение доверительного интервала. В примере 2 (см. выше раздел Метод наименьших квадратов) регрессионное уравнение позволило предсказать значение переменной Y при заданном значении переменной X. В задаче о выборе места для торговой точки средний годовой объем продаж в магазине площадью 4000 кв. футов был равен 7,644 млн. долл. Однако эта оценка математического ожидания генеральной совокупности является точечной. Ранее для оценки математического ожидания генеральной совокупности была предложена концепция доверительного интервала. Аналогично можно ввести понятие доверительного интервала для математического ожидания отклика при заданном значении переменной X:

где , = b₀ + b₁X_i – предсказанное значение переменное Y при X = X_i, S_YX – среднеквадратичная ошибка, n – объем выборки, X_i — заданное значение переменной X, µ_Y|_X=Xi – математическое ожидание переменной Y при Х = Х_i, SSX =

Анализ формулы (13) показывает, что ширина доверительного интервала зависит от нескольких факторов. При заданном уровне значимости возрастание амплитуды колебаний вокруг линии регрессии, измеренное с помощью среднеквадратичной ошибки, приводит к увеличению ширины интервала. С другой стороны, как и следовало ожидать, увеличение объема выборки сопровождается сужением интервала. Кроме того, ширина интервала изменяется в зависимости от значений X_i. Если значение переменной Y предсказывается для величин X, близких к среднему значению , доверительный интервал оказывается уже, чем при прогнозировании отклика для значений, далеких от среднего.

Допустим, что, выбирая место для магазина, мы хотим построить 95%-ный доверительный интервал для среднего годового объема продаж во всех магазинах, площадь которых равна 4000 кв. футов:

Следовательно, средний годовой объем продаж во всех магазинах, площадь которых равна 4 000 кв. футов, с 95% -ной вероятностью лежит в интервале от 6,971 до 8,317 млн. долл.

Вычисление доверительного интервала для предсказанного значения. Кроме доверительного интервала для математического ожидания отклика при заданном значении переменной X, часто необходимо знать доверительный интервал для предсказанного значения. Несмотря на то что формула для вычисления такого доверительного интервала очень похожа на формулу (13), этот интервал содержит предсказанное значение, а не оценку параметра. Интервал для предсказанного отклика Y_X=Xi при конкретном значении переменной X_i определяется по формуле:

Предположим, что, выбирая место для торговой точки, мы хотим построить 95%-ный доверительный интервал для предсказанного годового объема продаж в магазине, площадь которого равна 4000 кв. футов:

Следовательно, предсказанный годовой объем продаж в магазине, площадь которого равна 4000 кв. футов, с 95%-ной вероятностью лежит в интервале от 5,433 до 9,854 млн. долл. Как видим, доверительный интервал для предсказанного значения отклика намного шире, чем доверительный интервал для его математического ожидания. Это объясняется тем, что изменчивость при прогнозировании индивидуальных значений намного больше, чем при оценке математического ожидания.

Подводные камни и этические проблемы, связанные с применением регрессии

Трудности, связанные с регрессионным анализом:

• Игнорирование условий применимости метода наименьших квадратов.
• Ошибочная оценка условий применимости метода наименьших квадратов.
• Неправильный выбор альтернативных методов при нарушении условий применимости метода наименьших квадратов.
• Применение регрессионного анализа без глубоких знаний о предмете исследования.
• Экстраполяция регрессии за пределы диапазона изменения объясняющей переменной.
• Путаница между статистической и причинно-следственной зависимостями.

Широкое распространение электронных таблиц и программного обеспечения для статистических расчетов ликвидировало вычислительные проблемы, препятствовавшие применению регрессионного анализа. Однако это привело к тому, что регрессионный анализ стали применять пользователи, не обладающие достаточной квалификацией и знаниями. Откуда пользователям знать об альтернативных методах, если многие из них вообще не имеют ни малейшего понятия об условиях применимости метода наименьших квадратов и не умеют проверять их выполнение?

Исследователь не должен увлекаться перемалыванием чисел — вычислением сдвига, наклона и коэффициента смешанной корреляции. Ему нужны более глубокие знания. Проиллюстрируем это классическим примером, взятым из учебников. Анскомб показал, что все четыре набора данных, приведенных на рис. 23, имеют одни и те же параметры регрессии (рис. 24).

Рис. 23. Четыре набора искусственных данных

Рис. 24. Регрессионный анализ четырех искусственных наборов данных; выполнен с помощью Пакета анализа (кликните на рисунке, чтобы увеличить изображение)

Итак, с точки зрения регрессионного анализа все эти наборы данных совершенно идентичны. Если бы анализ был на этом закончен, мы потеряли бы много полезной информации. Об этом свидетельствуют диаграммы разброса (рис. 25) и графики остатков (рис. 26), построенные для этих наборов данных.

Рис. 25. Диаграммы разброса для четырех наборов данных

Диаграммы разброса и графики остатков свидетельствуют о том, что эти данные отличаются друг от друга. Единственный набор, распределенный вдоль прямой линии, — набор А. График остатков, вычисленных по набору А, не имеет никакой закономерности. Этого нельзя сказать о наборах Б, В и Г. График разброса, построенный по набору Б, демонстрирует ярко выраженную квадратичную модель. Этот вывод подтверждается графиком остатков, имеющим параболическую форму. Диаграмма разброса и график остатков показывают, что набор данных В содержит выброс. В этой ситуации необходимо исключить выброс из набора данных и повторить анализ. Метод, позволяющий обнаруживать и исключать выбросы из наблюдений, называется анализом влияния. После исключения выброса результат повторной оценки модели может оказаться совершенно иным. Диаграмма разброса, построенная по данным из набора Г, иллюстрирует необычную ситуацию, в которой эмпирическая модель значительно зависит от отдельного отклика (Х₈ = 19, Y₈ = 12,5). Такие регрессионные модели необходимо вычислять особенно тщательно. Итак, графики разброса и остатков являются крайне необходимым инструментом регрессионного анализа и должны быть его неотъемлемой частью. Без них регрессионный анализ не заслуживает доверия.

Рис. 26. Графики остатков для четырех наборов данных

Как избежать подводных камней при регрессионном анализе:

• Анализ возможной взаимосвязи между переменными X и Y всегда начинайте с построения диаграммы разброса.
• Прежде чем интерпретировать результаты регрессионного анализа, проверяйте условия его применимости.
• Постройте график зависимости остатков от независимой переменной. Это позволит определить, насколько эмпирическая модель соответствует результатам наблюдения, и обнаружить нарушение постоянства дисперсии.
• Для проверки предположения о нормальном распределении ошибок используйте гистограммы, диаграммы «ствол и листья», блочные диаграммы и графики нормального распределения.
• Если условия применимости метода наименьших квадратов не выполняются, используйте альтернативные методы (например, модели квадратичной или множественной регрессии).
• Если условия применимости метода наименьших квадратов выполняются, необходимо проверить гипотезу о статистической значимости коэффициентов регрессии и построить доверительные интервалы, содержащие математическое ожидание и предсказанное значение отклика.
• Избегайте предсказывать значения зависимой переменной за пределами диапазона изменения независимой переменной.
• Имейте в виду, что статистические зависимости не всегда являются причинно-следственными. Помните, что корреляция между переменными не означает наличия причинно-следственной зависимости между ними.

Резюме. Как показано на структурной схеме (рис. 27), в заметке описаны модель простой линейной регрессии, условия ее применимости и способы проверки этих условий. Рассмотрен t-критерий для проверки статистической значимости наклона регрессии. Для предсказания значений зависимой переменной использована регрессионная модель. Рассмотрен пример, связанный с выбором места для торговой точки, в котором исследуется зависимость годового объема продаж от площади магазина. Полученная информация позволяет точнее выбрать место для магазина и предсказать его годовой объем продаж. В следующих заметках будет продолжено обсуждение регрессионного анализа, а также рассмотрены модели множественной регрессии.

Рис. 27. Структурная схема заметки

[1] Используются материалы книги Левин и др. Статистика для менеджеров. – М.: Вильямс, 2004. – с. 792–872

[2] Если зависимая переменная является категорийной, необходимо применять логистическую регрессию.

Полное руководство по линейной регрессии в Scikit-Learn

Обсудим модель линейной регрессии, используемую в машинном обучении. Используем ML-техники для изучения взаимосвязи между набором известных показателей и тем, что мы надеемся предсказать. Давайте рассмотрим выбранные для примера данные, чтобы конкретизировать эту идею.

В бой. Импортируем рабочие библиотеки и датасет:

Вот краткое описание нашего датасета:

• CRIM — уровень преступности на душу населения по городам.
• ZN — доля земли под жилую застройку, разделенная на участки площадью более 25 000 кв. футов.
• INDUS — доля акров, которые принадлежат предприятиям, не связанным с розничной торговлей, на город.
• CHAS — фиктивная переменная реки Чарльз (1, если участок соединен с рекой; 0 в противном случае).
• NOX — концентрация оксидов азота (в десятимиллионных долях).
• RM — среднее количество комнат в доме.
• AGE — доля занимаемых зданий, построенных до 1940 г.
• DIS — взвешенные расстояния до пяти бостонских центров занятости.
• RAD — индекс доступности радиальных автомобильных дорог.
• TAX — полная ставка налога на имущество за каждые 10000 долларов стоимости.
• PTRATIO — соотношение учеников и учителей по городам.
• B — 1000 (Bk — 0,63) , где Bk — доля граждан афроамериканского происхождения по городам.
• LSTAT — процент более низкого статуса населения.
• TARGET —медианное значение стоимости занимаемых домов в тысячах долларов США.

Задача данной выборки сводится к прогнозированию целевого показателя (медианной стоимости недвижимости), используя приведенные выше показатели (все, кроме TARGET).

Линейная регрессия

Как мы можем подойти к этой проблеме?
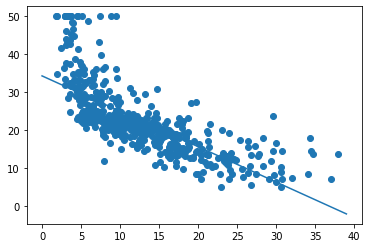
Для нашего первого прохода давайте упростим задачу. Допустим, мы просто хотим использовать признак LSAT для прогнозирования TARGET.

По оси X у нас есть LSTAT, а по оси Y — TARGET. Просто взглянув на это, можно увидеть отрицательную взаимосвязь: когда LSTAT растет, TARGET падает.

Функция оценки/стоимости

Как мы можем решить проблему предсказания TARGET на основе LSTAT? Хорошая отправная точка для размышлений: допустим, мы разрабатываем множество моделей для прогнозирования целевого показателя, как нам выбрать лучшую из них? Как только мы найдем подходящее для сравнения значение, наша задача — минимизировать/максимизировать его.

Это чрезвычайно полезно, если вы можете свести проблему к единственной оценочной метрике. Тогда это очень упрощает цикл разработки модели. Однако в реальном мире прийти к такому упрощению может быть непросто. Иногда не совсем понятно, что вы хотите, чтобы ваша модель максимизировала/минимизировала. Но это проблема для другой статьи.

Поэтому для нашей задачи предлагаю использовать среднюю квадратическую ошибку (mean squared error) в качестве оценочной метрики. Для лучшего понимания смысла MSE, давайте определимся с терминологией:

Таким образом, MSE:

По сути, для каждой точки мы вычитаем предсказанное нами значение из фактического. Затем, поскольку нас не волнует направление ошибки, мы возводим разницу в квадрат. Наконец, мы вычисляем среднее всех этих значений. Таким образом, мы хотим, чтобы среднее расстояние между предсказанными и фактическими показателями было минимальным.

Вам может быть интересно, почему мы возводили разницу в квадрат вместо того, чтобы брать абсолютное значение. Оказывается, что для некоторых из представленных ниже математических операций возведение в квадрат работает лучше. Кроме того, это метод максимального правдоподобия. Тем не менее, такой подход приводит к тому, что крупные ошибки имеют более сильное влияние на среднее значение, поскольку мы возводим в квадрат каждое отклонение.

Наша модель

Теперь, когда у нас есть функция оценки, как найти способ ее минимизировать? В этом посте мы рассмотрим модель линейной регрессии. Она выглядит следующим образом:

Где j — количество имеющихся у нас предсказателей (независимых переменных), значения бета — это наши коэффициенты. А бета 0 является смещением (intercept). По сути, данная модель представляет собой линейную комбинацию наших предсказателей с intercept.

Теперь, когда у нас есть модель и функция оценки, наша задача состоит в том, чтобы найти бета-значения, которые минимизируют MSE для наших данных. Для линейной регрессии на самом деле существует решение в замкнутой форме, называемое нормальным уравнением. Однако в этом посте мы собираемся использовать другую технику — градиентный спуск.

Градиентный спуск

Градиентный спуск — это метод, который мы позаимствовали из оптимизации. Очень простой, но мощный алгоритм, который можно использовать для поиска минимума функции.

1. Выберите случайное начальное значение.
2. Делайте шаги, пропорциональные отрицательному градиенту в текущей точке.
3. Повторяйте, пока не достигните предела.

Этот метод найдет глобальный минимум, если функция выпуклая. В противном случае мы можем быть уверены только в том, что достигнем локальный минимум.

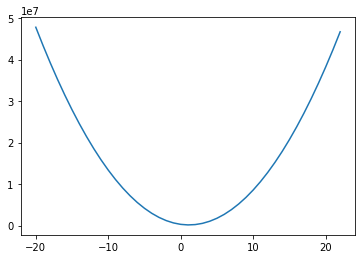
Первый вопрос, на который нам нужно ответить: является ли наша функция оценки выпуклой? Давайте посмотрим:

Для построения графика выше мы взяли диапазон значений коэффициентов для LSTAT, и для каждого из них рассчитали MSE на основе наших данных. Если мы затем отобразим полученные значения, мы получим приведенную выше кривую — выглядит довольно выпуклой! И оказывается, что наша функция MSE с нашей моделью линейной регрессии всегда будет выпуклой! Это означает: мы можем использовать градиентный спуск, чтобы найти оптимальные коэффициенты для нашей модели!

Одна из причин того, что градиентный спуск более распространен, чем нормальное уравнение для машинного обучения, заключается в том, что он намного лучше масштабируется по мере увеличения количества показателей. Это также стандартный метод оптимизации, который используется повсюду в машинном обучении. Поэтому понимание того, как он работает, чрезвычайно важно.

Градиенты

Если вы снова посмотрите на наш псевдокод для градиентного спуска, вы увидите, что на самом деле все, что нам нужно сделать, это вычислить градиенты. Итак, что такое градиенты? Это просто частные производные по коэффициентам. Для каждого имеющегося коэффициента нам нужно будет вычислить производную MSE по этому коэффициенту. Давайте начнем!

Для начала запишем выражение для MSE, подставив функцию оценки со смещением и единственной переменной LSTAT:

Теперь, взяв производную по бета 0, мы получим (умноженное на -1):

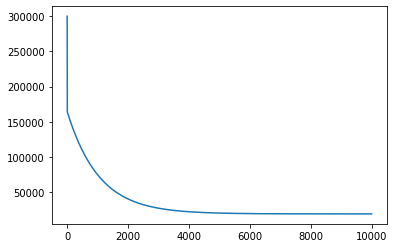
Теперь давайте запустим наш алгоритм градиентного спуска и убедимся, что MSE действительно уменьшается:

Первый график, представленный выше, показывает значение MSE, когда мы запускаем градиентный спуск. Как и следовало ожидать, MSE уменьшается со временем по мере выполнения алгоритма. Это означает, что мы постоянно приближаемся к оптимальному решению.

На графике видно, что мы вполне могли завершить работу раньше. MSE переходит в прямую (почти не изменяется) примерно после 4000 итераций.

Итак, запуск градиентного спуска показал, что оптимальное смещение составляет 34.55, а оптимальный наклон равен -0,95. На приведенном выше графике эта линия показана поверх наших данных, она выглядит как аппроксимирующая прямая.

Скорость обучения

Один параметр, который нам еще предстоит обсудить, — это скорость обучения. Эта скорость — гиперпараметр, используемый для определения того, насколько большие шаги мы делаем от направления градиента. Как узнать, какое значение выбрать? Как правило, можно попробовать множество вариантов. Вот некоторые из них, которые были предложены Andrew Ng: .001, .003, .01, .03, .1, .3, 1, 3.

Выбор слишком малого значения приводит к более медленной сходимости. Выбор слишком большого значения может привести к перешагиванию через минимум и расхождению.

Существуют также другие оптимизаторы градиентного спуска, которые более сложны и адаптируют скорость обучения за вас. Это также то, что вы можете делать самостоятельно, постепенно снижая скорость обучения.

Когда прекратить итерацию?

В моем коде я просто выполняю наш цикл 10000 раз. Почему 10000? Никакой реальной причины, кроме моей уверенности в том, что этого достаточно, чтобы достичь минимума. Такой подход точно нельзя назвать лучшей практикой. Вот несколько более разумных идей:

1. Следите за оценкой после каждого цикла, и когда ее очередное изменение меньше некоторого граничного значения — скажем, 0.001 — останавливайтесь.
2. Используйте проверочный датасет (validation set) и отслеживайте число ошибок, например, с помощью MSE. Когда метрика перестанет уменьшаться, остановитесь.

Нормализация данных

При работе с градиентным спуском вы хотите, чтобы все ваши данные были нормализованы. Вычтите среднее значение и разделите на стандартное отклонение для всех ваших тренировочных показателей. Обычно это ускоряет обучение и снижает вероятность застревания в локальном оптимуме, если функция оценки не является выпуклой.

Другие виды градиентного спуска

Показанный здесь градиентный спуск представляет собой классическую форму, что означает: каждое обновление коэффициента использует все данные для вычисления градиентов. Существует также стохастический градиентный спуск. Ему необходима только 1 строка данных (1 наблюдение) для пересчета коэффициентов в каждом цикле.

Такой способ намного лучше масштабируется, так как нужно обработать только одну строку данных за раз перед обновлением. Также он является более неопределенным, поскольку вы пытаетесь перемещаться с использованием градиента, рассчитанного на основе единственного наблюдения.

Другой тип градиентного спуска — это мини-пакетный градиентный спуск. Эта форма представляет собой компромисс между двумя, где вы выбираете размер пакета. Скажем, 32 (или, что еще лучше, пакетный график, который начинается с небольших пакетов и увеличивается с увеличением количества эпох), и каждая итерация вашего градиентного спуска использует 32 случайные строки данных для вычисления градиента (алгоритм воспользуется всеми строками перед повторной выборкой раннее обработанных). В результате мы получаем некоторую масштабируемость, но и некоторую неопределенность.

Такое случайное поведение оказывается полезным для функций оценки, которые не являются выпуклыми (глубокое обучение), поскольку оно может помочь модели избежать локального минимума. Это наиболее распространенный метод для невыпуклых функций оценки.

Допущения нашей модели

Всякий раз, когда вы имеете дело с моделью, хорошо знать, какие допущения она делает. Университет Дьюка написал об этом целую статью:

Реализация линейной регрессии в Scikit-Learn

Теперь, когда мы немного разбираемся в теории и реализации, давайте обратимся к библиотеке scikit-learn, чтобы на самом деле использовать линейную регрессию на наших данных. Написание моделей с нуля довольно полезно для обучения, но на практике вам, как правило, гораздо лучше использовать проверенную и широко используемую библиотеку.

Для начала нужно нормализовать данные:

У Scikit-learn довольно удобный API. Он предоставляет множество моделей, и все они имеют функции fit и predict . Вы можете вызвать fit с вашими X и y данными для обучения модели, а затем использовать predict для получения предсказанных значений на основе новых данных. Scikit-learn также предоставляет множество метрик, которые вы можете использовать для оценки, такие как MSE. Здесь я вычисляю среднеквадратическую ошибку (RMSE). Так мы можем использовать шкалу нашего целевого показателя, что, легче для понимания.

SGDRegressor выполняет линейную регрессию с использованием градиентного спуска и принимает следующие аргументы: tol (сообщает модели, когда следует прекратить итерацию) и eta0 (начальная скорость обучения).

RMSE в итоге составила 4.68… для нашей обучающей выборки с использованием scikit-learn.

Полиномиальные переменные

Рассматривая построенный выше график стоимости от LSTAT, вы могли заметить, что между данными показателями существует полиномиальная связь. Линейная регрессия хорошо подходит в случае линейной зависимости, но, если вы добавите полиномиальные показатели, такие как LSTAT, вы сможете установить более сложные отношения. SKLearn упрощает данный процесс:

Функция PolynomialFeatures сгенерировала новую матрицу показателей, состоящую из всех их полиномиальных комбинаций со степенью меньше или равной указанной (в нашем примере 2). Затем мы нормализовали эти данные и скормили их нашей модели. Так мы получили улучшенную тренировочную RMSE, равную 3.24. Однако обратите внимание, что эти результаты, представленные в иллюстративных целях, используют только тренировочную выборку.

Категориальные переменные

Линейная регрессия — одна из моделей, с которой нужно быть осторожным, когда у вас есть качественные данные. Если у вас переменные со значениями 1, 2 и 3, которые на самом деле означают «Мужской», «Женский», «Нет ответа», не передавайте их модели таким образом, даже если они являются числами.

Если бы вы это сделали, модель присвоила бы такому показателю коэффициент — возможно, 0.1. Это будет означать, что принадлежность к женскому полу увеличивает предсказанное значение на 0.1. А отсутствие ответа — на 0.2. Но, возможно, метка «Женский» должна повысить результат на 1.2, а «Нет ответа» — всего на 0.001. Чтобы решить данную проблему, вы должны преобразовать такие значения в фиктивные переменные, чтобы каждая категория имела свой собственный вес. Вы можете узнать, как это сделать с помощью scikit-learn, здесь.

Интерпретация вашей модели

Линейная регрессия — это отличная статистическая модель, которая существует уже давно. Есть много статистических методов, которые можно использовать для ее оценки и интерпретации. Мы не будем рассматривать их все и на самом деле сосредоточимся на очень простых подходах, которые, возможно, более распространены в машинном обучении, чем в статистике.

Во-первых, давайте посмотрим на коэффициенты, которым научилась наша модель (по всем показателям):

Что они означают? Каждый коэффициент представляет собой среднее изменение цены на жилье при изменении соответствующего показателя на единицу с условием, что все остальные показатели остаются неизменными. Например, если значения других показателей не затрагиваются, то увеличение LSTAT на единицу снижает наш целевой показатель (цену на жилье) на 3.72, а увеличение RM увеличивает его на 2.85.

Таким образом, если вы хотите повысить стоимость дома, то может быть стоит начать с увеличения RM и уменьшения LSTAT. Я говорю «может быть», потому что линейная регрессия рассматривает корреляции. Судя по нашим данным, такая взаимосвязь имеет место быть, что само по себе не означает обязательное наличие причинно-следственной связи между показателями.

Доверительные интервалы

Часто в машинном обучении очень полезно иметь доверительный интервал вокруг ваших оценок. Есть разные способы сделать это, но одним довольно общим методом является использование bootstrap .

Bootstrap — это случайная выборка на основе наших данных, и эта выборка того же размера, что и исходные данные. Так мы можем создать несколько представлений одних и тех же данных. Давайте создадим 1000 bootstrap-семплов наших данных.

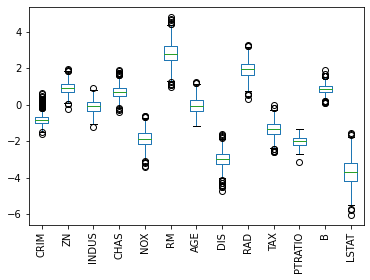
Затем мы обучим модель на каждом из полученных датасетов и получим следующие коэффициенты:

На представленной диаграмме размаха показан диапазон значений коэффициентов, которые мы получили для каждого показателя для всех моделей, которые мы обучили. AGE — особенно интересен, потому что значения коэффициентов были как положительными, так и отрицательными, что является хорошим признаком того, что, вероятно, нет никакой связи между возрастом и стоимостью.

Кроме того, мы можем увидеть, что LSTAT имеет большой разброс в значениях коэффициентов, в то время как PTRATIO имеет относительно небольшую дисперсию, что повышает доверие к нашей оценке этого коэффициента.

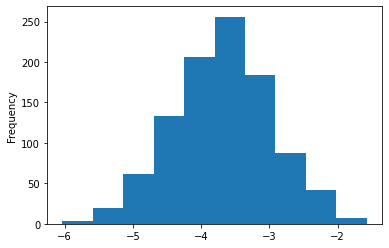
Мы даже можем немного углубиться в полученные коэффициенты для LSTAT:

Теперь мы можем с большой уверенностью сказать, что фактический коэффициент LSTAT отрицателен и почти наверняка находится между -2 и -5.5.

Разделение на обучающий/тестовый датасеты и кросс-валидация

До этого момента мы тренировались на всех имеющихся данных. Это может иметь смысл, потому что мы хотим максимизировать их полезность, используя как можно больше данных для обучения. С другой стороны, из-за такого подхода нам становится труднее оценивать, насколько хорошо работает наша модель. Причина этого в том, что, если мы продолжим рассчитывать MSE, используя тренировочные данные, мы можем обнаружить, что при применении модели на незнакомых ей данных, она работает довольно плохо.

Эта идея называется переобучением (overfitting). По сути, такая модель работает намного лучше с обучающими данными, чем с новыми. Она была чрезмерно натренирована на обнаружение уникальных характеристик обучающего множества, которые не являются общими закономерностями, присущими генеральной совокупности.

Другая сторона проблемы называется bias. Модель имеет высокий bias, когда она плохо обучена. В этом случае MSE будет высокой как для тренировочных данных, так и для данных, не показанных во время обучения.

В ML всегда существует компромисс между смещением (bias) и дисперсией (overfitting). По мере того, как ваши модели становятся более сложными, возрастает риск переобучения на тренировочных данных.

Теперь, когда мы знаем о проблемах с вычислением MSE, используя только обучающее множество, что мы можем сделать, чтобы лучше судить о способности модели к обобщению? А также диагностировать overfitting и bias? Типичным решением является разделение наших данных на две части: обучающий и тестовый датасеты.

Теперь, когда у нас есть два отдельных набора данных, мы можем тренировать модель на обучающем множестве и вычислять метрики, используя оба датасета (лучше всего использовать ваши тестовые данные после настройки модели):

Отлично! Теперь у нас есть MSE как для тренировочных данных, так и для данных тестирования. И оба значения довольно близки, что говорит об отсутствии проблемы с переобучением. Но достаточно ли они низкие? Большие значения предполагают наличие высокого bias.

Один из способов разобраться в этом — построить график обучения. Кривая обучения отображает нашу функцию ошибок (MSE) с различными объемами данных, используемых для тренировки. Вот наш график:

Вы можете видеть, что с менее чем 50 обучающими примерами тренировочная MSE неплохая, а кросс-валидация оставляет желать лучшего — довольно плохая (мы еще не говорили о кросс-валидации, так что пока думайте об этом как о тестировании). Если бы у нас было только такое количество данных, это выглядело бы как явная проблема высокой дисперсии (переобучения).

По мере увеличения наших данных мы начинаем улучшать оба результата, и они становятся очень похожими, что говорит о том, что у нас нет проблемы переобучения. Как правило, при высокой дисперсии на этом графике две линии будут находится довольно далеко друг от друга, и кажется, что, если мы продолжим добавлять больше данных, они могут сойтись.

Этот график больше похож на проблему с большим смещением (bias), поскольку две наши кривые очень близки и сглаживаются. Однако трудно сказать наверняка, потому что, возможно, мы только что достигли наилучшего возможного MSE. В таком случае это не будет проблемой высокого смещения. Такой результат был бы ей только в том случае, если бы наши кривые выровнялись при значении MSE выше оптимального. В реальной жизни вы не знаете, какова оптимальная MSE, поэтому вам нужно немного поразмышлять, считаете ли вы, что уменьшение bias улучшит ваш результат — но лучше просто попробуйте!

Устранение проблем высоких bias/variance

Итак, теперь, когда вы диагностировали проблему смещения или дисперсии, как ее исправить?

Для высокой дисперсии:

• Получите больше данных для обучения
• Попробуйте меньший набор показателей
• Используйте менее сложную модель
• Добавьте регуляризацию

Для высокого смещения:

• Попробуйте увеличить число показателей
• Перейдите на более сложную модель

Кросс-валидация и настройка гиперпараметров

Ранее мы упоминали этот термин: кросс-валидация. Давайте поговорим об этом сейчас. На данный момент мы узнали, что неплохо разделить данные на наборы для обучения и тестирования, чтобы лучше понять, насколько хорошо работает модель. Это замечательно, но представьте, что мы хотим протестировать несколько разных моделей или протестировать разные параметры нашей модели — например, другую скорость обучения или толерантность. Как бы нам решить, какая модель или какой параметр лучше? Будем ли мы обучать все на тренировочных данных и тестировать все на наших тестовых данных?

Надеюсь, вы понимаете, что это не имеет смысла, потому что тогда мы, по сути, оказались бы в том же месте, что и раньше, без возможности проверить, насколько хорошо мы справляемся с ранее неизвестными данными. Итак, мы хотим сохранить датасет для тестирования незапятнанным в том смысле, что в идеальном мире мы бы запускали наши тесты на нем только после того, как провели все необходимые эксперименты и были уверены в том, что нашли самую лучшую модель.

Похоже, нам нужен третий набор данных – датасет для валидации. По сути, мы можем разбить наши обучающие данные на две части: обучающий и проверочный датасеты. Все модели будут обучены на тренировочном множестве, а затем протестированы на нашем проверочном наборе. Затем мы выберем модель, которая лучше всего справляется с проверкой, и посмотрим, насколько удачно она пройдет тестирование. Результаты тестирования покажут, как хорошо наша модель будет работать с незнакомыми данными, и на этом мы завершим процесс разработки.

Примечание: в статье предполагается, что используемые тестовые и проверочные датасеты представляют собой репрезентативные выборки из нашей совокупности. Например, если средняя цена дома в вашем проверочном множестве составляет 1 миллион, а для генеральной совокупности соответствующее значение равно 300 тысячам, у вас плохая выборка. Часто мы случайным образом делим имеющиеся данные на три выборки, но всегда полезно подтвердить, что эти наборы являются репрезентативными. В противном случае вы обнаружите, что ваша модель, которая хорошо зарекомендовала себя при проверке и тестировании, плохо работает на реальных данных.

На практике вместо создания единого множества для проверки мы часто используем k-блочную кросс-валидацию.

Это означает, что мы выбираем значение k, скажем 3. Затем мы берем наши обучающие данные и делим их на 3 части. Мы случайным образом выбираем 2 блока для тренировки, а затем используем оставшийся для тестирования. Повторяем этот процесс еще 2 раза, так чтобы все наблюдения были использованы как для обучения, так и для проверки, и каждое из них применялось для валидации только один раз. После этого усредняем все три оценки (в нашем случае MSE), чтобы получить общую оценку для конкретной модели. Затем мы можем повторить этот процесс для других моделей, чтобы найти лучшую.

Вот видео, которое более наглядно описывает этот подход (с русскими субтитрами): https://www.youtube.com/watch?v=TIgfjmp-4BA

Этот процесс довольно просто реализуется с помощью sklearn:

Здесь мы фактически использовали рандомизированный поиск ( RandomizedSearchCV ), который обычно лучше, чем поиск по всем возможным значениям. Часто вы хотите попробовать много разных параметров для множества различных регуляторов, и сеточный поиск (перебор всех возможных комбинаций) вам не подходит.

Обычно вы хотите использовать рандомизированный поиск (случайный выбор комбинаций), как мы сделали выше. Хотя, поскольку у нас было только небольшое количество значений, мы заставили его работать как сеточный поиск, установив n_iter_search равным числу вариантов, которые мы хотели попробовать.

Мы также установили cv=3 , чтобы иметь 3 блока и использовали отрицательную MSE, потому что функции CV в scikit-learn пытаются максимизировать значение.

Вы можете узнать больше о случайном и «сеточном» вариантах поиска здесь: https://scikit-learn.org/stable/modules/grid_search.html.

Кроме того, в scikit-learn есть много других CV функций, которые полезны, особенно если вы хотите протестировать разные модели с одинаковыми блоками. Вот некоторая документация: https://scikit-learn.org/stable/modules/cross_validation.html.

Регуляризация

В качестве средства борьбы с высокой дисперсией я упомянул регуляризацию. Вы можете думать о ней как о методе, который используется для наказания модели за обучение сложным взаимосвязям. Для линейной регрессии она принимает форму трех популярных подходов. Все эти методы сосредоточены на идее ограничения того, насколько большими могут быть коэффициенты наших показателей.

Идея состоит в том, что если мы переоцениваем влияние предсказателя (большое значение коэффициента), то, вероятно, мы переобучаемся. Примечание: у нас все еще могут быть просто большие коэффициенты. Регуляризация говорит о том, что уменьшение MSE должно оправдывать увеличение значений коэффициентов.

• Регуляризация L1 (Lasso): вы добавляете сумму абсолютных значений коэффициентов к функции оценки. Этот метод может принудительно обнулить коэффициенты, что затем может быть средством выбора показателей.
• Регуляризация L2 (Ridge): вы добавляете сумму квадратов значений коэффициентов к функции оценки.
• Эластичная сетка: вы добавляете обе и выбираете, как их утяжелить.

Каждый из этих методов принимает весовой множитель, который говорит вам, насколько сильное влияние регуляризация будет иметь на функцию оценки. В scikit-learn такой параметр называется альфа. Альфа равный 0 не добавит штрафа, в то время как высокое его значение будет сильно наказывать модель за наличие больших коэффициентов. Вы можете использовать кросс-валидацию, чтобы найти хорошее значение для альфа.
Sklearn упрощает это: