Реферат: Отделение корней. Графический и аналитический методы отделения корней
| Название: Отделение корней. Графический и аналитический методы отделения корней Раздел: Рефераты по информатике Тип: реферат Добавлен 11:03:33 16 июня 2011 Похожие работы Просмотров: 2994 Комментариев: 22 Оценило: 8 человек Средний балл: 4.5 Оценка: 5 Скачать |
| Из рис.1 видно, что корень находится на отрезке [1,2]. В качестве приближенного значения этого корня можно взять значение х=1.5. Если взять шаг по оси Ох меньше, то и значение корня можно получить более точное. |
3. Аналитический метод (табличный или шаговый).
Для отделения корней полезно помнить следующие известные теоремы:
1) если непрерывная функция f(x) принимает значения разных знаков на концах отрезка [a,b], т.е. f(a)f(b) 0, значит корня на отрезке [0;0.5] нет.
f(0.5)f(1) 0, значит корня на отрезке [0.5;0.75] нет.
3.1. Отделение корней нелинейного уравнения
Отделение корней – это определение их наличия, количества и нахождение для каждого их них достаточно малого отрезка [a, b], которому он принадлежит.
На первом этапе определяется число корней, их тип. Определяется интервал, в котором находятся эти корни, или определяются приближенные значения корней.
В инженерных расчетах, как правило, необходимо определять только вещественные корни. Задача отделения вещественных корней решается Аналитическими и Графическими методами.
Аналитические методы основаны на функциональном анализе.
Для алгебраического многочлена n-ой степени (полинома) с действительными коэффициентами вида
Pn(x) = an x n + an-1xn-1 +. +a1x+ a0 = 0, (an >0) (3.2)
Верхняя граница положительных действительных корней 

Где: k ³ 1 – номер первого из отрицательных коэффициентов полинома;
B – максимальный по модулю отрицательный коэффициент.
Нижнюю границу положительных действительных корней 

Если для этого уравнения по формуле Лагранжа верхняя граница равна R1, то


Тогда все положительные корни многочлена лежат в интервале


Интервал отрицательных действительных корней многочлена определяется с использованием следующих вспомогательных функций.






Рассмотрим пример отделения корней с использованием этого аналитического метода.
Методом Лагранжа определим границы положительных и отрицательных корней многочлена.
3×8 – 5×7 – 6×3 – x – 9 = 0
K = 1 B = |– 9| an = 3


 |
k = 8 B = 3 an = 9
Отсюда границы положительных корней 0,5 ≤ x+ ≤ 4



K = 1 B = 6 an = 9
 |
Следовательно, границы отрицательных корней –2 ≤ x– ≤ –0,6
Формула Лагранжа позволяет оценить интервал, в котором находятся все действительные корни, положительные или отрицательные. Поэтому, для определения расположения каждого корня необходимо проводить дополнительные исследования.
Для трансцендентных уравнений не существует общего метода оценки интервала, в котором находятся корни. Для этих уравнений оцениваются значения функции в особых точках: разрыва, экстремума, перегиба и других.
На практике получил большее распространение Графический метод приближённой оценки вещественных корней. Для этих целей строится график функции по вычисленным её значениям.
Графически корни можно отделить 2-мя способами:
1. Построить график функции y = f(x) и определить координаты пересечений с осью абсцисс− это приближенные значения корней уравнения.На графике 3 корня.
Рис. 3.1 Отделение корней на графике f(x).
2. Преобразовать f(x)=0 к виду j(x) = y(x), где j(x) и y(x) – элементарные функции, и определить абсциссу пересечений графиков этих функций.
На графике 2 корня.
Рис. 3.2 Отделение корней по графикам функций j(x) и y(x).
Графический метод решения нелинейных уравнений широко применяется в технических расчётах, где не требуется высокая точность.
Для отделения вещественных корней можно использовать ЭВМ. Алгоритм отделения корней основан на факте Изменения знака функции в окрестности корня. Действительно, если корень вещественный, то график функции пересекает ось абсцисс, а знак функции изменяется на противоположный.
Рассмотрим Схему алгоритма отделения корней нелинейного уравнения на заданном отрезке в области определения функции.
Алгоритм позволяет определить приближённые значения всех действительных корней на отрезке [a, b]. Введя незначительные изменения в алгоритм, его можно использовать для определения приближённого значения максимального или минимального корня.
Приращение неизвестного Δx не следует выбирать слишком большим, чтобы не «проскочить» два корня.
Недостаток метода – использование большого количества машинного времени.
Графическое отделение корней
Графическое отделение корнейосновано на графическом способе решения уравнений – отыскании точек, в которых функция f(x)пересекает ось 0Х.
Пример 1.2.2-1. Отделить корни уравнения ln (x-1) 2 – 0.5 = 0.
На рис. 1.2.2-1 изображен график функции y = ln (x-1) 2 – 0.5, из которого следует, что уравнение имеет два действительных корня 

 |
В некоторых случаях удобно вначале преобразовать функцию f(x) к виду f(x)=g1(x)— g2(x), из которого, при условии f(x)=0, следует, что g1(x)=g2(x). При построении графиков y1=g1(x)и y2=g2(x)находят отрезки, содержащие точки пересечения этих графиков.
Пример 1.2.2-2. Отделить корни уравнения сos(x) – x + 1 = 0.
Приведем исходное уравнение к виду сos(x)= x – 1. Построив графики функций y1 = сos(x) и y2 = х – 1 (рис. 1.2.2), выделим отрезок, содержащий корень 
 |
Аналитическое отделение корней
Аналитическое отделениекорней основано на следующей теореме.
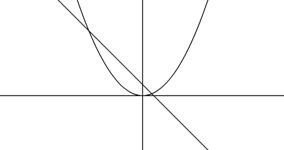
Если функция f(x) непрерывна и монотонна на отрезке [a;b] и принимает на концах отрезка значения разных знаков, то на отрезке [a;b] содержится один корень уравнения f(x)=0.
Действительно, если условия теоремы выполнены, как это имеет место на отрезке [a;b] (рис. 1.2.2-3), то есть f(a)∙f(b) 0 для xÎ [a;b], то график функции пересекает ось 0Х только один раз и, следовательно, на отрезке [a;b] имеется один корень 
Аналогично можно доказать единственность корня 

 |
Таким образом, для отделения корней нелинейного уравнения необходимо найти отрезки, в пределах которых функция монотонна и изменяет свой знак. Принимая во внимание, что непрерывная функция монотонна в интервалах между критическими точками, при аналитическом отделении корней уравнения можно рекомендовать следующий порядок действий:
1)установить область определения функции;
2)определить критические точки функции, решив уравнение f¢(x)=0;
3)составить таблицу знаков функции f(x) в критических точках и на границах области определения;
4)определить интервалы, на концах которых функция принимает значения разных знаков.
Пример 1.2.2-3. Отделить корни уравнения x — ln(x+2) = 0.
Область допустимых значений функции f(x) = x — ln(x+2) лежит в интервале (-2; ∞), найденных из условия x+2>0. Приравняв производную f¢(x)=1-1/(x+2) к нулю, найдем критическую точку хk= -1. Эти данные сведены в табл. 1.2.2-1 и табл. 1.2.2-2 знаков функции f(x).
Таблица 1.2.2-1 Таблица 1.2.2-.2
| x | x→-2 | -1 | x→∞ | x | -1.9 | -1.1 | -0.9 | 2.0 |
| Sign(f(x)) | + | — | + | Sign(f(x)) | + | — | — | + |
Уравнение x — ln(x+2) = 0 имеет два корня 



Уточнение корней
Задача уточнения корня уравнения 



http://matica.org.ua/metodichki-i-knigi-po-matematike/vychislitelnaia-matematika/3-1-otdelenie-kornei-nelineinogo-uravneniia
http://megaobuchalka.ru/11/54487.html
 Министерство образования и науки РФ
Министерство образования и науки РФ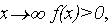 при
при 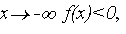 что уже свидетельствует о наличии хотя бы одного корня.
что уже свидетельствует о наличии хотя бы одного корня.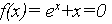 видим, что
видим, что 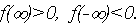 Обнаружив, что
Обнаружив, что 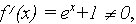 устанавливаем факт наличия единственного корня, и остается лишь найти его (как говорится, за немногим стало дело).
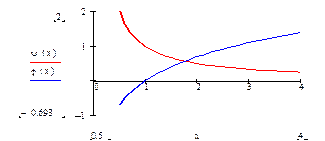
устанавливаем факт наличия единственного корня, и остается лишь найти его (как говорится, за немногим стало дело).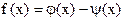 и строить графики функций
и строить графики функций 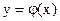 и
и 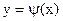 . Абсцисса точки пересечения этих графиков и будет являться корнем уравнения (1), а отрезок на оси абсцисс которому принадлежит данный корень, будет являться интервалом изоляции. Этот метод отделения корней хорошо работает только в том случае, если исходное уравнение не имеет близких корней. Данный метод дает тем точнее результат, чем мельче берется сетка по оси Ох.
. Абсцисса точки пересечения этих графиков и будет являться корнем уравнения (1), а отрезок на оси абсцисс которому принадлежит данный корень, будет являться интервалом изоляции. Этот метод отделения корней хорошо работает только в том случае, если исходное уравнение не имеет близких корней. Данный метод дает тем точнее результат, чем мельче берется сетка по оси Ох.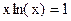 .
.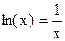 , т.е.
, т.е. 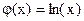 и
и 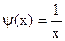 .
.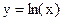 и
и 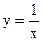 .
.