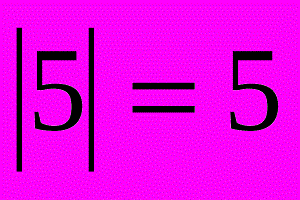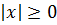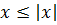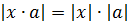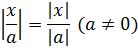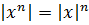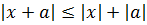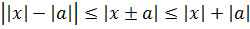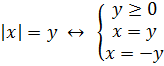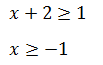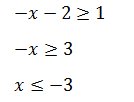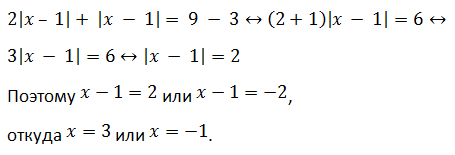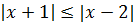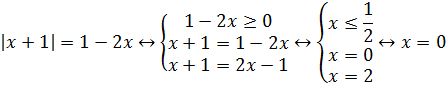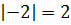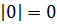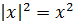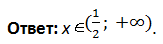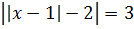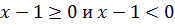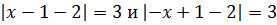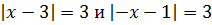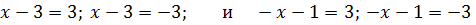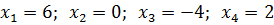График уравнения с абсолютными величинами

Научно-исследовательская работа «Графический методиуравнений, содержащих абсолютную величину»

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

«Актуальность создания школьных служб примирения/медиации в образовательных организациях»

Свидетельство и скидка на обучение каждому участнику

Выберите документ из архива для просмотра:

Выбранный для просмотра документ АННОТАЦИЯ.docx

МБОУ Абалаковская СОШ№1, номинация 5-8класс

Тема: «Графический метод решения уравнений с абсолютной величиной»

Руководитель: Бусыгина Ирина Владимировна, учитель математики высшей категории

Цель исследовательской работы: исследование возможности рационального построения графиков с модулями для решения уравнений, содержащих модуль и параметр .

В данной работе анализируются графические методы построения графиков функции с модулем, содержащей один, два и вложенные модули первой степени. Кроме того,автор показывает применение рациональных методов для решения уравнений с модулем и параметром.

Работа имеет практическую направленность, т.к. материал может использоваться в качестве репетитора для подготовки ЕГЭ, ОГЭ заданий повышенного уровня и проведения математических факультативов, развивая математическую культуру учащихся.

Выбранный для просмотра документ Графический метод.ppt

Описание презентации по отдельным слайдам:

Графический метод решения линейных уравнений с абсолютной величиной Задания на решение уравнений с модулем и параметрами — это одна из самых трудных тем математики (10 класс, профильный уровень) Решение заданий 2й части ЕГЭ и ОГЭ (повышенный уровень)

Цель: Исследование возможности рационального построения графиков с модулями для решения линейных уравнений, содержащих модуль и параметр

Задачи Изучить теорию по решению методов уравнений с модулем. Научиться решать уравнения, содержащие знак абсолютной величины Классифицировать графические методы решения уравнений. Проанализировать достоинства и недостатки каждого метода Применить рациональные методы для решения уравнений

Тип1.Графики ,содержащие 1 модуль y=|x| y=|x| a y=|x a| 1.Определение модуля 2.Метод симметрии (2шага) 3.Использование алгоритма преобразований функций у=кх+в

x a>2 — два корня a=2 — один корень a

Выбранный для просмотра документ Работа.doc

Задания на построение графиков функции «модуль» и задачи с параметрами традиционно — это одна из самых трудных тем математики, поэтому она всегда включена в задания повышенного и высокого уровня ГИА и ЕГЭ.

Понятие «модуль» изучается в школе с 6 класса, причем на уровне ,только определения и вычисления, несмотря на то, что он широко применяется во многих разделах школьного курса математики, например, в изучении абсолютной и относительной погрешностей приближенного числа; в геометрии и физике будут изучаться понятия вектора и его длины (модуля вектора). Понятия модуля применяется в курсах высшей математики, физики и технических наук, изучаемых в высших учебных заведениях.

Перед выпускниками стоит проблема – удачно сдать ГИА в 9классе, а в дальнейшем и ЕГЭ.

В этом году на уроках математики мы познакомились с понятием линейной функции и научились строить ее график. Было показано, что этот ее график берется за основу построения функции «модуль». Кроме того, учитель сказала, что уравнения бывают с одним и несколькими модулям. Я решила глубже изучить эту тему, тем более, что она мне пригодится при сдаче экзаменов.

Тема «Графический метод решения уравнений, содержащих абсолютную величину»

Цель работы : исследование возможности рационального построения графиков с модулями для решения уравнений, содержащих модуль и параметр

Изучить теорию по решению методов уравнений с модулем.

Научиться решать уравнения 1 й степени, содержащие знак абсолютной величины.

Классифицировать графические методы решения уравнений.

Проанализировать достоинства и недостатки различных методов построения графиков функции «модуль».

Узнать, что такое параметр

Применить рациональные методы для решения уравнений с параметром

Объект – методы решения уравнений с модулем

Предмет графический метод решения уравнений

Методы исследования: теоретические и практические:

теоретические — это изучение литературы по теме исследования; интернет – информации;

практические- это анализ информации, полученной при изучении литературы, результатов, полученных при решении уравнений с модулем различными способами;

сравнение способов решения уравнений предмет рациональности их использования при решении различных уравнений с модулем.

Понятия и определения

1.1.Понятие «модуль» широко применяется во многих разделах школьного курса математики, например, в изучении абсолютной и относительной погрешностей приближенного числа; в геометрии и физике изучаются понятия вектора и его длины (модуля вектора). Понятия модуля применяется в курсах высшей математики, физики и технических наук, изучаемых в высших учебных заведениях.

Слово «модуль» произошло от латинского слова « modulus », что в переводе означает «мера». Это слово имеет множество значений и применяется не только в математике, физике и технике, но и в архитектуре, программировании и других точных науках.Считают, что термин предложил использовать Котс, ученик Ньютона. Знак модуля был введен в XIX веке Вейерштрассом.

В архитектуре модуль– исходная единица измерения, устанавливаемая для данного архитектурного сооружения.В технике – это термин, применяемый в различных областях техники, служащий для обозначения различных коэффициентов и величин, например, модуль упругости, модуль зацепления.В математике модуль имеет несколько значений, но я буду рассматривать его как абсолютную величину числа.

Определение: Модулем (абсолютной величиной) действительного числа а называется само это число, если а ≥0, или противоположное число – а, если а 0, у=-кх+в, где х 0.Часть прямой при х x |+ n график сдвигается вверх по оси ординат на в единиц

б) у=| x |- n график сдвигается вниз по оси ординат

с) у=| x + n | график сдвигается влево по оси абцисс

d )у=| x — n | график сдвигается вправо по оси абцисс

1.3.4. Метод интервалов. Координатная прямая разбивается на интервалы и полуинтервалы нулями модулей. Далее, используя определение модуля, для каждой из найденных областей получим уравнение, которое необходимо решить на данном промежутке и получить функцию.

1.3.5. Метод расширения областей нулей. В том случае, когда модулей несколько, удобнее не раскрывать модули, а использовать следующее утверждение: алгебраическая сумма модулей n линейных выражений представляет собой кусочно-линейную функцию, график которой состоит из n +1 прямолинейных отрезков.

Тогда график может быть построен по n+2 точкам, n из которых представляют собой корни внутримодульных выражений, ещё одна — произвольная точка с абсциссой, меньшей меньшего из этих корней и последняя — с абсциссой, большей большего из корней.

1.4. Имеем уравнение ax+b=c. В этом уравнении х – неизвестное, a,b,c – коэффициенты, которые могут принимать различные числовые значения. Заданные таким образом коэффициенты называются параметрами. Одно уравнение с параметрами задает множество уравнений (для всех возможных значений параметров).

это все уравнения, которые задает уравнение с параметрами ax+b=c.

Решить уравнение с параметрами – это значит:

Указать, при каких значениях параметров уравнение имеет корни и сколько их при разных значениях параметров.

Найти все выражения для корней и указать для каждого из них те значения параметров, при которых это выражение определяет корень уравнения.

Таким образом, существуют разные методы построения графиков с модулем, которые необходимо исследовать на возможность их рационального применения.

Анализ методов построения графиков функций, содержащих модуль, и применение

«График – это говорящая линия,

которая может о многом рассказать»

2.1. Изучая виды уравнений с модулем, мы увидели, что их можно и разделить по типам и методам решения.

Таблица. Классификация типов уравнений и их методов решения.

1.Уравнение с одним модулем

|xn|=a

|x|n=a

1.По определению модуля

2.Уравнение, содержащее 2 модуля

|xn||xm|=a

1.По определению модуля

|||xn|m||= а

1.По определению модуля

Вывод: таким образом, классификация уравнений дает нам общие методы решения всех типов уравнений — это по определению модуля и графический метод.

2.2.Анализ построения графиков.

2.2.1. Тип 1. Построение у=| x |

1.Строим прямую у=х

2.Выделяем часть прямой при х0

3.Строим прямую у=-х

4.Выделяем часть прямой при х x -2|

1.Строим прямую у=х-2

2.Выделяем часть прямой при х-20

3.Строим прямую у=-х+2

4.Выделяем часть прямой при х-2 По определению модуля

По определению главного модуля имеем:

2) х 0 и у=-х+1 х 0 у=х-1 х Определение модуля

Знать : как определяются координаты точек прямых

Уметь выделять часть прямой по неравенству

Уметь строить точки по их координатам

Уметь вычислять координаты точек

-применение большого объема знаний

-при «снятии» модуля можно допустить ошибки

Знать и уметь применять преобразование функции

Строить симметрию относительно оси абцисс

-знание алгоритмов преобразования графиков

Находить нули модуля

Определять интервалы и полуинтервалы

Приводить подобные слагаемые

Уметь строить точки по их координатам

-много вычислений и преобразований при снятии нулей

-занимает много времени

-правильность определения интервалов и полуинтервалов

Метод расширения области нулей

Находить нули модуля

Уметь расширять область нулей

Уметь вычислять модули в этих точках

Уметь строить точки по их координатам

— допуск ошибок в вычислениях

Метод преобразований функций

Знать алгоритм преобразования

Уметь строить точки по их координатам

Уметь вычислять координаты точек

Уметь применять алгоритм преобразования

— знание алгоритмов преобразования графиков

Вывод: анализируя таблицу, делаем вывод, что метод симметрии и расширения области нулей самые рациональные, т.к. содержат меньше всего действий для построения, а значит экономят времени.

2.3.Применение рациональных методов построения графиков к решению уравнений с модулем и параметром

2.3.1. Решить уравнение :

Строим у= и у=0,5-х

4.Проводим отрезки и лучи

2.3.2. ЕГЭ 2009г. Найдите все значения а, при каждом из которых уравнение , имеет ровно 1 корень.

Решение:

,

Преобразуем:-4+а=3 и-4+а=-3

— +7=а — -1=а

Построим графики функций у = а, , .

При а =7 прямая пересекает график только в одной точке. Значит, данное уравнение имеет ровно один корень при а =7.

2.3.3. ЕГЭ 2010г. При каком значении параметра уравнение имеет 4 корня а =|||х |-2|-2 | ?

Решение: применив поэтапно метод симметрию:

Первый раз: у=

Построим прямую у=а

Ответ: при а=2 уравнение имеет 4корня

Таким образом, в ходе проделанной работы нам удалось изучить и проанализировать разные методы построения графиков. В результате анализа и сравнения методов построения графиков получили следующие выводы:

-перевод алгебраической задачи на язык графиков позволяет избежать громоздких решений;

-при решении уравнений, содержащих модуль и параметр, графический способ является более наглядным и сравнительно более простым;

-при построении графиков, содержащих 2 модуля и «матрешку» практичнее метод симметрии;

-хотя графический способ решения уравнений является приближенным, т.к. точность зависит от выбранного единичного отрезка, толщины карандаша, углов под которыми пересекаются линии и т.д., но этот метод позволяет оценивать кол-во корней уравнений для решения уравнений с параметром.

Учитывая, что одни из самых популярных заданий на ЕГЭ и ГИА уравнения с модулем, то , что главным моим результатом является то, что я могу решать уравнения с модулем и параметром графическим способом.

Модуль числа знак, свойства, действия, как найти, примеры графиков

Модуль числа легко найти, и теория, которая лежит в его основе, важна при решении задач.

Свойства и правила раскрытия, используемые при решении упражнений и на экзаменах, будут полезны школьникам и студентам.

Что такое модуль в математике

Модуль числа описывает расстояние на числовой линии от нуля до точки без учета того, в каком направлении от нуля лежит точка. Математическое обозначение: |x|.

Иными словами, это абсолютная величина числа. Определение доказывает, что значение никогда не бывает отрицательным.

Свойства модуля

Важно помнить о следующих свойствах:

1. Правило раскрытия: абсолютная величина любого числа больше или равна нулю:
2. Если абсолютные значения содержат выражения противоположных значений, они равны:
3. Значение числа не превышает величину его модуля:
4. Правило раскрытия при произведении:
5. Правило, применимое при делении:
6. При возведении в степень:
7. Сумма величин:
8. Двойной модуль:

Модуль комплексного числа

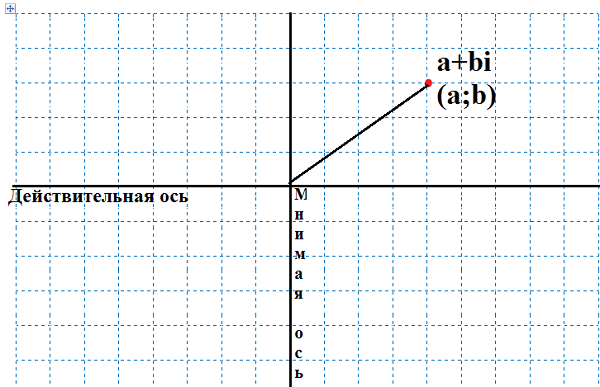
Абсолютной величиной комплексного числа называют длину направленного отрезка, проведенного от начала комплексной плоскости до точки (a, b).

Этот направленный отрезок также является вектором, представляющим комплексное число a + bi, поэтому абсолютная величина комплексного числа – это то же самое, что и величина (или длина) вектора, представляющего a+ bi.

Как решать уравнения с модулем

Уравнение с модулем – это равенство, которое содержит выражение абсолютного значения. Если для действительного числа оно представляет его расстояние от начала координат на числовой линии, то неравенства с модулем являются типом неравенств, которые состоят из абсолютных значений.

Уравнения типа |x| = a

Уравнение |x| = a имеет два ответа x = a и x = –a, потому что оба варианта находятся на координатной прямой на расстоянии a от 0.

Равенство с абсолютной величиной не имеет решения, если величина отрицательная.

Если |x| &lt, a представляет собой расстояние чисел от начала координат, это значит, что нужно искать все числа, чье расстояние от начала координат меньше a.

Уравнения типа |x| = |y|

Когда есть абсолютные значения по обе стороны уравнений, нужно рассмотреть обе возможности для приемлемых определений – положительные и отрицательные выражения.

Например, для равенства |x − a| = |x + b| есть два варианта: (x − a) = − (x + b) или (x − a) = (x + b).

Далее простая арифметика − нужно решить два равенства относительно x.

Уравнения типа |x| = y

Уравнения такого вида содержат абсолютную величину выражения с переменной слева от нуля, а справа – еще одну неизвестную. Переменная y может быть как больше, так и меньше нуля.

Для получения ответа в таком равенстве нужно решить систему из нескольких уравнений, в которой нужно убедиться, что y – неотрицательная величина:

Решение неравенств с модулем

Чтобы лучше понять, как раскрыть модуль в разных типах равенств и неравенств, нужно проанализировать примеры.

Уравнения вида |x| = a

Пример 1 (алгебра 6 класс). Решить: |x| + 2 = 4.

Решение.

Такие уравнения решаются так же, как и равенства без абсолютных значений. Это означает, что, перемещая неизвестные влево, а константы – вправо, выражение не меняется.

После перемещения константы вправо получено: |x| = 2.

Поскольку неизвестные связаны с абсолютным значением, это равенство имеет два ответа: 2 и −2.

Ответ: 2 и −2.

Пример 2 (алгебра 7 класс). Решить неравенство |x + 2| ≥ 1.

Решение.

Первое, что нужно сделать, это найти точки, где абсолютное значение изменится. Для этого выражение приравнивается к 0. Получено: x = –2.

Это означает, что –2 – поворотная точка.

Далее определяется знак на интервалах: на промежутке величина будет отрицательной, а на интервале будет положительной.

Разделим интервал на 2 части:

Общим ответом для этих двух неравенств является интервал [−1, + ∞).

Общим ответом для этих двух неравенств является интервал (−∞, –3].

Окончательное решение – объединение ответов отдельных частей:

Ответ: x ∈ (–∞, –3] ∪ [–1, + ∞).

Уравнения вида |x| = |y|

Пример 1 (алгебра 8 класс). Решить уравнение с двумя модулями: 2 * |x – 1| + 3 = 9 – |x – 1|.

Решение:

Ответ: x1 = 3, x2 = − 1.

Пример 2 (алгебра 8 класс). Решить неравенство:

Решение:

Уравнения вида |x| = y

Пример 1 (алгебра 10 класс). Найти x:

Решение:

Очень важно провести проверку правой части, иначе можно написать в ответ ошибочные корни. Из системы видно, что не лежит в промежутке .

Ответ: x = 0.

Модуль суммы

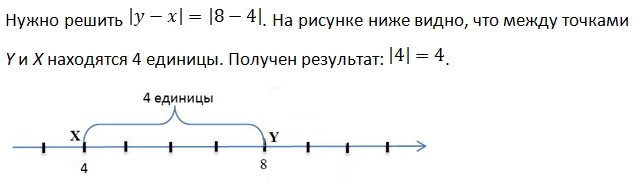
Модуль разности

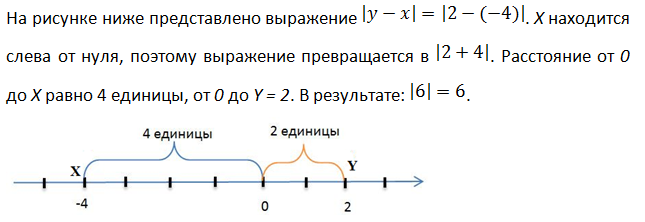
Абсолютная величина разности двух чисел x и y равна расстоянию между точками с координатами X и Y на координатной прямой.

Пример 1.

Пример 2.

Модуль отрицательного числа

Для нахождения абсолютного значения числа, которое меньше нуля, нужно узнать, как далеко оно расположено от нуля. Поскольку расстояние всегда является положительным (невозможно пройти «отрицательные» шаги, это просто шаги в другом направлении), результат всегда положительный. То есть,

Проще говоря, абсолютная величина отрицательного числа имеет противоположное значение.

Модуль нуля

Вот почему нельзя сказать, что абсолютная величина – положительное число: ноль не является ни отрицательным, ни положительным.

Модуль в квадрате

Модуль в квадрате всегда равен выражению в квадрате:

Примеры графиков с модулем

Часто в тестах и на экзаменах встречаются задания, которые возможно решить, лишь проанализировав графики. Рассмотрим такие задания.

Пример 1.

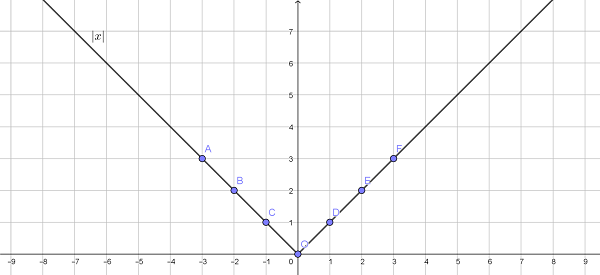
Дана функция f(x) = |x|. Необходимо построить график от – 3 до 3 с шагом 1.

Решение:

Объяснение: из рисунка видно, что график симметричен относительно оси Y.

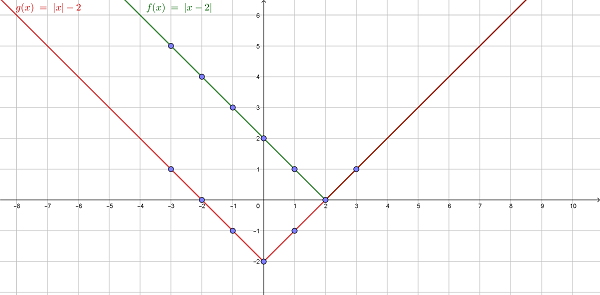
Пример 2. Необходимо нарисовать и сравнить графики функций f(x) = |x–2| и g(x) = |x|–2.

Решение:

Объяснение: константа внутри абсолютной величины перемещает весь график вправо, если ее значение отрицательное, и влево, если положительное. Но постоянная снаружи будет передвигать график вверх, если значение положительное, и вниз, если оно отрицательное (как –2 в функции g (x)).

Координата вершины x (точка, в которой соединяются две линии, вершина графа) – это число, на которое график сдвигается влево или вправо. А координата y – это значение, на которое график сдвигается вверх или вниз.

Строить такие графики можно с помощью онлайн приложений для построения. С их помощью можно наглядно посмотреть, как константы влияют на функции.

Метод интервалов в задачах с модулем

Метод интервалов – один из лучших способов найти ответ в задачах с модулем, особенно если в выражении их несколько.

Для использования метода нужно совершить следующие действия:

1. Приравнять каждое выражение к нулю.
2. Найти значения переменных.
3. Нанести на числовую прямую точки, полученные в пункте 2.
4. Определить на промежутках знак выражений (отрицательное или положительное значение) и нарисовать символ – или + соответственно. Проще всего определить знак с помощью метода подстановки (подставив любое значение из промежутка).
5. Решить неравенства с полученными знаками.

Пример 1. Решить методом интервалов.

Решение:

Результатом будет сумма всех подходящих интервалов.

Модуль в модуле

Среди примеров часто встречаются уравнения, где нужно найти корни равенств такого вида: ||ax – b| – c| = kx + m.

Лучше всего понять принцип на примере.

Пример 1. Решить

Решение:

Первым делом нужно раскрыть внутренний модуль. Для этого рассматривается два варианта:

В первом случае выражение положительное, а во втором отрицательное. Исходя из этого, получаем:

Нужно упростить два уравнения:

Далее каждое из равенств разделяется еще на два:

Получено четыре результата:

Заключение

Самое важное, что нужно знать: модуль не может быть отрицательным.

Поэтому, если представлено выражение, похожее на |2 – 4x| = –7 стоит помнить, что равенство неверно даже без поисков ответов.

В качестве итогов, напомним все свойства, которые помогут в решении задач:

• когда положительное число находится внутри модуля, достаточно просто избавиться от него,
• если есть выражение, нужно его упростить, прежде чем найти абсолютное значение,
• если равенство содержит две переменные, нужно решать его с помощью системы уравнений и за основу брать методы решения выражений с абсолютными величинами.

Решать равенства и неравенства можно разными способами, но лучше всего использовать графический способ или метод интервалов.

Урок-лекция по математике по теме «Построение графиков, содержащих модуль»

Разделы: Математика

Цель урока: обобщить и систематизировать материал данной темы.

План лекции (написать на доске)

а) повторить определение модуля
б) геометрическая интерпретация модуля
в) графики простейших функций, содержащих модуль
г) графики уравнений содержащих модули
д) построить графики функций ( самостоятельно)

Ход урока

1. Орг. момент

2. Содержание материала

2а. Повторить определение модуля

Модуль — абсолютная величина числа, равная расстоянию от начала отсчета до точки на числовой прямой.

Определение. Модуль числа a или абсолютная величина числа a равна a, если a больше или равно нулю и равна -a, если a меньше нуля:

Из определения следует, что для любого действительного числа a,

Геометрически |a| означает расстояние на координатной прямой от точки, изображающей число a, до начала отсчета.

Если то на координатной прямой существуют две точки a и -a, равноудаленные от нуля, модули которых равны.

Если a = 0, то на координатной прямой |a| изображается точкой 0.

2б. Использование геометрической интерпретации модуля

Геометрический смысл модуля разности величин — это расстояние между ними. Например, геометрический смысл выражения |x – a| — длина отрезка координатной оси, соединяющей точки с абсциссами а и х. Перевод алгебраической задачи на геометрический язык часто позволяет избежать громоздких решений.

Пример 1. Решим уравнение |x – 2| + |x – 3|=1 с использованием геометрической интерпретации модуля.

Будем рассуждать следующим образом: исходя из геометрической интерпретации модуля, левая часть уравнения представляет собой сумму расстояний от некоторой точки с абсциссой х до двух фиксированных точек с абсциссами 2 и 3. Тогда очевидно, что все точки с абсциссами из отрезка [2; 3] обладают требуемым свойством, а точки, расположенные вне этого отрезка — нет. Отсюда ответ: множеством решений уравнения является отрезок [2; 3].

Ответ: х [2; 3]

Пример 2. Решим уравнение |x – 1| — |x – 2|=1 с использованием геометрической интерпретации модуля.

Разность расстояний до точек с абсциссами 1 и 2 равна единице только для точек, расположенных на координатной оси правее числа 2. Следовательно, решением данного уравнения будет являться не отрезок, заключенный между точками 1 и 2, а луч, выходящий из точки 2, и направленный в положительном направлении оси х.

Ответ: х [2; +)

Обобщением вышеприведенных уравнений являются следующие равносильные переходы:

2в Графики простейших функций, содержащих знак абсолютной величины

Под простейшими функциями понимают алгебраическую сумму модулей линейных выражений.

В том случае, когда модулей несколько, удобнее не раскрывать модули, а использовать следующее утверждение:

алгебраическая сумма модулей n линейных выражений представляет собой кусочно-линейную функцию, график которой состоит из n +1 прямолинейных отрезков.

Тогда график может быть построен по n+2 точкам, n из которых представляют собой корни внутримодульных выражений, ещё одна — произвольная точка с абсциссой, меньшей меньшего из этих корней и последняя — с абсциссой, большей большего из корней.

1) f(x)=|x — 1|. Вычисляя функции в точках 1, 0 и 2, получаем график, состоящий из двух отрезков (рис.1);

2) f(x)=|x — 1| + |x – 2|. Вычисляя значение функции в точках с абсциссами 1, 2, 0 и 3, получаем график, состоящий из двух отрезков прямых (рис.2);

3) f(x)=|x — 1| + |x – 2| + |x – 3|. Для построения графика вычислим значения функции в точках 1, 2, 3, 0 и 4 (рис.3);

4) f(x)=|x — 1| — |x – 2|. График разности строится аналогично графику суммы, т.е. по точкам 1, 2, 0 и 3 (рис.4).

Рис. 1. Рис. 2. Рис. 3. Рис. 4.

2г Графики уравнений, содержащих модули

Когда в “стандартные” уравнения прямых, парабол, гипербол включают знак модуля, их графики становятся необычными и даже красивыми. Чтобы научиться строить такие графики, надо владеть приемами построения “базовых” фигур, а также твердо знать и понимать определение модуля числа.

Покажем на примерах некоторые приемы построения графиков уравнений с модулями.

Пример 3. Построим график уравнения y=|x 2 -4|.

Сначала построим параболу y=x 2 -4. Чтобы получить из нее график уравнения y=|x 2 — 4|, нужно каждую точку параболы с отрицательной ординатой заменить точкой с той же абсциссой, но с противоположной (положительной) ординатой. Иными словами, часть параболы, расположенную ниже оси х, нужно заменить линией, ей симметричной относительно оси х.

Пример 4. Построим график уравнения y=х 2 -2|x|.

По определению модуля числа, заменим формулу y=х 2 -2|x| двумя, задающими зависимость переменной y от x отдельно для x > 0 и x 0, то y=х 2 -2x;

Строить график будем так:

• построим параболу y=х 2 -2x и обведем ту ее часть, которая соответствует неотрицательным значениям х, т.е. часть, расположенную правее оси у;
• в той же координатной плоскости построим параболу y=х 2 +2x и обведем ту ее часть, которая соответствует отрицательным значениям х, т.е. часть, расположенную левее оси у.

Обведенные части парабол вместе образуют график уравнения y=х 2 -2|x|

Здесь при построении графика удобно использовать сдвиги вдоль осей координат. Будем действовать по следующему плану:

1. Построим “основной” график, т.е. график уравнения y=|х|;
2. Подвинем построенный график на 2 единицы вниз; получится график уравнения y=|х|-2;
3. Часть графика, расположенную ниже оси х, заменим ее “зеркальным отражением”, т.е. заменим ее линией, симметричной относительно оси х; получится график уравнения y=||х|-2|;
4. Сдвинем построенный в п.3 график на 2 единицы вниз; получится график уравнения y=||х|-2|-2;
5. Часть графика, расположенную ниже оси х, отобразим симметрично относительно этой оси; получим график уравнения y=|||х|-2|-2|.

3. Используя вышеизложенные правила построить самостоятельно графики других уравнений, содержащих модули:

(дать выполнить это задание дома)

Построить графики функций:

1)y=|2x + 4|
2) y=|x 2 – 3|
3) y=|x 2 – x – 2|
4) y=
5) y=|x| – 2x
6) y=x 2 +3|x|
7) y=(5–|x|)(|x|+1)
8) y=(5–|x|)(x+1)
9) y=||x|-3|
10) y=|||x|-4|-4|

4. Подвести итог урока:

Подводя итог урока надо нацелить учащихся на то, что это первый шаг для решения уравнений содержащих модуль и параметр. Этот урок можно проводить в 9-м классе, 10-м классе и 11-м классе перед темой: решение уравнений с параметрами.