График уравнения с двумя переменными видео

7 класс, 8 урок, Линейное уравнение с двумя переменными и его график

Просмотров: 39 858

29 сентября 2017

Mr. event

Спасибо, все понял

Troll Zach

Я вот думаю, это я такой тупой или это потому-что я основ не знаю?

Troll Zach

Мы это в девятом классе учим, а тут седьмой написанно.
Это как?

Спасибо, очень хороший урок!

samson Кудрин

спасибо огромное. Я сейчас в седьмом классе и у меня была истерика потому что я не понимал эту тему, а ты мне очень сильно помог.

Николай Форточкин

Спасибо большое, супер

MORGAN

Аделина Умаханова

Блин я ничего не поняла вот реально какие плоскости какие блин координаты оффффф блин что мне делать ??))))

1234-пydi

СПАСИБОО, я всё смогла понять!

MaScH1N1ST

капец умный, у меня мотемотичка так хорошо не объясняет

Артём Спивачук

Единственный из многих блогеров, который всё понятно объясняет!

CHILLSIDE

У нас бы так математичка объясняла)

eykenov

Cody star

Ниче не понял а завтра сам работа а к репититору ток в четверг пойду

mallek

Спасибо большое Я до этого не понимал тему

Нурайым Беккожа

Извините,
А если уравнение
4x+y-2=0?
Просто понять никак не могу ахах

Вот зачем убиваться в школе 45мин когда этот чувак объясняет за 5мин

Спс пацан я хор понел

Оала Члвв

Иван Бирюков

7 класс, 8 урок, Линейное уравнение с двумя переменными и его график

Легитимность Чеченской Республики Ичкерия. Часть- 3

Убитая путиным Анна Политковская, о геноциде

Желтое платье своими руками/ Making a summer dress from scratch in 4 hours

5 десятилетий назад

5 десятилетий назад

Линейное уравнение с двумя переменными. 7 класс.

MEKTEП OnLine MATEMATИKA

7 класс, 9 урок, Линейная функция и её график

Видеокурсы DA VINCI

Алгебра 7 Линейное уравнение с двумя переменными и его график

Образование. Обучение — Znaika TV. Знайка.ру

Как решать системы уравнений с двумя переменными

Что такое система уравнений с двумя переменными

Системой уравнений в алгебре называется некое условие, смысл которого заключается в одновременном выполнении нескольких уравнений относительно нескольких (либо одной) переменных.

Это значит, что система представляет собой комплекс уравнений. Данные равенства могут содержать одну, две или более переменных. Основным условием понятия «система уравнений» является то, что все эти уравнения выполняются в одно время.

Объединить уравнения в систему можно с помощью фигурной скобки:

У р а в н е н и е 1 У р а в н е н и е 2 У р а в н е н и е 3 …

Графический метод решения

Принцип решения систем уравнений графическим способом заключается в построении графиков для каждого уравнения в общей системе координат. Тогда решения системы соответствуют точкам, в которых данные графики пересекаются. После объяснения решения ответ принято записывать, как координаты этих точек.

Разберем наглядный пример. Предположим, что дана некая система уравнений, решать которую нужно графическим способом. Выполним работу последовательно:

1. Запишем систему.
2. Выразим одну из переменных (пусть это будет у).
3. Построим на координатной прямой графики функций.
4. Найдем точки пересечения графиков.

2 x + 3 y = 12 3 x — y = 7 ⇔ y = 4 — 2 3 x y = 3 x — 7

Заметим, что точка пересечения графиков имеет следующие координаты:

Графический метод решения систем уравнений уступает в точности другим способам. Использовать график целесообразно в том случае, когда в задаче записана система линейных уравнений. Подобные задачи встречаются в средних классах школы. Такие уравнения имеют вид y = a x + b без квадратных членов, а их графики являются прямыми.

Метод подстановки

Алгоритм решения системы уравнений с помощью метода подстановки:

• выражение одной переменной через другие;
• подстановка выражения, которое получилось, в начальные уравнения на место выраженной переменной;
• повторение второго шага до тех пор, пока не будут определены другие переменные.

Рассмотрим последовательность действий на практике. Предположим, что имеется некая система уравнений, которую требуется решить:

2 x + 3 y = 12 3 x — y = 7

Выразим у из второго уравнения:

Выполним подстановку полученного выражения в первое равенство:

2 x + 3 3 x — 7 = 12

Для полученного уравнения с одной переменной несложно найти корни:

2 x + 3 3 x — 7 = 12

2 x + 3 · 3 x — 3 · 7 = 12

2 x + 9 x — 21 = 12

Зная х, выполним подстановку и найдем у:

y = 3 x — 7 = 3 · 3 — 7 = 2 .

Запишем в ответ значения двух переменных.

Ответ: x = 3 ; y = 2 , либо (3;2).

Метод сложения

При сложении левых частей пары (или более) уравнений выражение, полученное в результате, равно сложенным правым частям этих же равенств, согласно формуле:

a = b c = d ⇒ a + c = b + d

В обратную сторону записанное свойство не работает:

a + c = b + d ◃ ≠ ▹ a = b c = d

Таким образом, при решении систем уравнений можно увеличивать обе части уравнения на одинаковое число. Например, сложим первое уравнение с числом с:

a = b c = d ⇒ a + c = b + c

Исходя из того что c=d, можно выполнить замену c на d справа:

a = b c = d ⇒ a + c = b + c ⇒ a + c = b + d .

В качестве примера попробуем решить систему уравнений:

2 x + y = 12 3 x — y = 3

Следуя правилу, суммируем уравнения. В процессе левые части складываем друг с другом. Аналогичным образом поступим с правыми частями равенств. В результате:

2 x + y = 12 3 x — y = 3 ⇒ 2 x ¯ ¯ + y ¯ + 3 x ¯ ¯ — y ¯ = 15 ⇔ 5 x = 15 ⇔ x = 3 .

Получилось избавиться от переменной у. В итоге задача значительно упростилась. Подставим число 3 на место слагаемого с х:

2 x + y = 12 x = 3 ⇔ 2 · 3 + y = 12 x = 3 ⇔ y = 6 x = 3

В следующем примере система уравнений имеет следующий вид:

2 x + 3 y = 13 4 x + 5 y = 23

Заметим, что с помощью сложения задание не получится упростить. В этом случае можно воспользоваться умножением уравнения на какое-либо число, отличное от нуля. Важно выбрать такой множитель, который позволит избавиться от одной из переменных. В этом случае лучше использовать (-2):

2 x + 3 y = 13 · — 2 4 x + 5 y = 23 ⇔ — 4 x — 6 y = — 26 4 x + 5 y = 23

Приступим к сложению:

— 4 x — 6 y = — 26 4 x + 5 y = 23 ⇒ — 4 x — 6 y + 4 x + 5 y = — 26 + 23 ⇔ — y = — 3 ⇔

Выполним подстановку у=3 в первое уравнение:

2 x + 3 y = 13 y = 3 ⇔ 2 x + 9 = 13 y = 3 ⇔ x = 2 y = 3

Задания для самостоятельного решения

Нужно решить систему уравнений:

13 x + 6 y = 7 2 x — 4 y = 6

Выразим х с помощью второго уравнения:

Найти значения переменных:

2 x + 5 y = 10 8 y — 5 x = 57

Из первого равенства выразим х:

2 x + 5 y = 10 2 x = 10 — 5 y

Подставим полученное значение во второе уравнение и запишем ответ.

Дана система уравнений, которую требуется решить:

2 x + 5 y = 10 3 x — 2 y = 1

В данном случае следует умножить первое уравнение на число 2, а второе равенство умножить на число 5:

2 x + 5 y = 10 · 2 3 x — 2 y = 1 · 5 ⇔ 4 x + 10 y = 20 15 x — 10 y = 5

После сложения уравнений остается лишь определить х:

19 x = 25 ⇔ x = 25 19

При подстановке х в какое-либо из двух уравнений можно вычислить у и записать ответ.

Ответ: ( 25 19 ; 28 19 ) .

Требуется найти переменные:

3 y — 4 x = — 13 3 x + 7 y = 56

Здесь следует в первую очередь найти произведение первого уравнения и числа 3, умножить второе уравнение на множитель 4. Далее остается суммировать уравнения и записать ответ.

Нужно решить систему уравнений:

7 x + 3 y = 21 4 y — 5 x = — 15

Множителем для первого уравнения является число 4. Второе уравнение нужно умножить на -3. Полученные равенства следует сложить и записать ответ.

Решить систему уравнений:

6 x — 8 y = — 2 9 x + 10 y = 8

В данном случае предполагается умножение уравнений на дробные числа. Множителем для первого уравнения является дробь 1 4 . Второе уравнение следует умножить на 1 5 :

6 x — 8 y = — 2 · 1 4 9 x + 10 y = 8 · 1 5 ⇔ 6 4 x — 2 y = — 1 2 9 5 x — 2 y = 8 5

Далее выполним сложение:

6 4 x — 2 y = — 1 2 9 5 x — 2 y = 8 5 ⇔ 3 2 x + 9 5 x =-0,5+1,6 ⇔ ⇔ 15 10 x + 18 10 x = 1,1 ⇔ 33 10 x = 1 , 1 ⇔ ⇔ 33 = 11 x x = 3

Путем подстановки определим y:

6 3 — 8 y = — 2 x = 3 ⇔ — 8 y = — 4 x = 3 ⇔ y = 2 x = 3

Найти корни следующих систем уравнений:

2 x + 3 y = 11 3 x + 2 y = 9

3 x — y = 85 5 x + 2 y = 17

x — 3 y = 6 2 y — 5 x = — 4

y 4 — x 5 = 6 x 15 + y 12 = 0

y — x = 5 x + 3 y = 3

Ответ: (1; 3), (17; -34), (0; -2), (-15; 12), (-3; 2).

Урок «Уравнение с двумя переменными и его график»

Краткое описание документа:

Видеоурок «Уравнение с двумя переменными и его график» знакомит учеников с понятием уравнения с двумя переменными, его решением, дает представление о графике уравнения с двумя переменными, его построении. Задача видеоурока – наглядно представить учебный материал по данной теме, облегчая выполнение задач учителя на уроке и давая возможность ему более эффективно использовать время урока.

Возможности видеоурока больше, чем любого другого наглядного пособия. Возможность использовать анимационные эффекты, заменить учителя в демонстрации построения графиков, чертежей, выполнение голосового сопровождения позволяет повысить эффективность урока, более рационально распределять время, удерживать внимание учеников на изучаемом материале.

Видеоурок начинается с представления темы. Ученикам представляются примеры уравнений с двумя переменными: 3х+4у=16, х 2 =9-у 2 , ху-8=0. Далее дается представление о решениях уравнения с двумя переменными. Демонстрируется подстановка значений переменных х=4 и у=1, которые превращают уравнение 3х+4у=16 в справедливое равенство. После объяснения сути решения уравнения, вводится понятие решения уравнения, которое в данном случае представляет собой пару чисел (4;1), в котором на первом месте представлено значение переменной х, а на втором – значение переменной у. Далее для запоминания учениками на экран выведено определение, что такое решение уравнения, которым называется пара значений для переменных, обращающая уравнение в верное равенство.

Уточняется особенность уравнения, имеющего две переменные — в большинстве случаев они имеют бесконечное множество решений. Вводится понятие равносильных уравнений, представляющих собой уравнения, имеющие одинаковое множество решений. Отмечается одинаковый способ определения степени целого уравнения, имеющего две переменные, и целого уравнения, имеющего одну переменную. Также уточняется, что уравнение, содержащее две переменные, у которого в левой части – многочлен, а в правой – 0, имеет степень, равной степени данного многочлена. Способом определения степени уравнения остается замена его равносильным уравнением таким образом, чтобы в левой части уравнения остался многочлен стандартного вида, а в левой – нуль. Приведен пример такой замены: отмечается, что уравнения (х 2 -у) 2 =х 4 -1 и -2х 2 у+у 2 +1=0 равносильны. После приведения уравнения к виду, когда в левой части остается многочлен стандартного вида, можно установить, что данное уравнение — третьей степени.

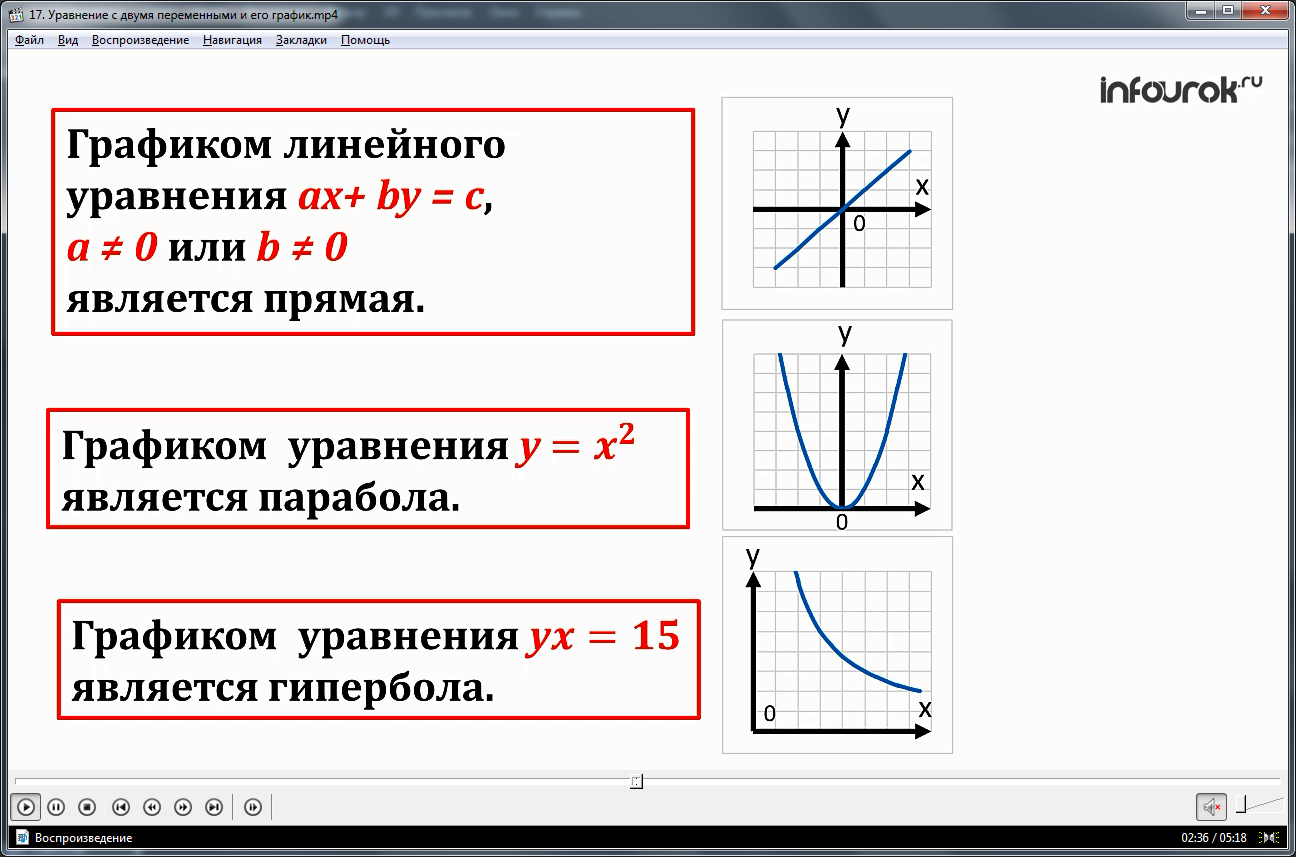
Далее рассматриваются особенности графика уравнения, имеющего две переменные. В представленном определении графиком некоторого уравнения, имеющего две переменные, является множество точек на координатной плоскости, подставив координаты которых, можно получить верное равенство. Ученикам напоминается вид графиков, уже изученных ранее и представляющих собой график уравнения с двумя переменными. Это прямая, представляющая собой график линейного уравнения ax+by=c, где a≠0 и b≠0, а также парабола – график уравнения у=х 2 , гипербола – график ух=15.

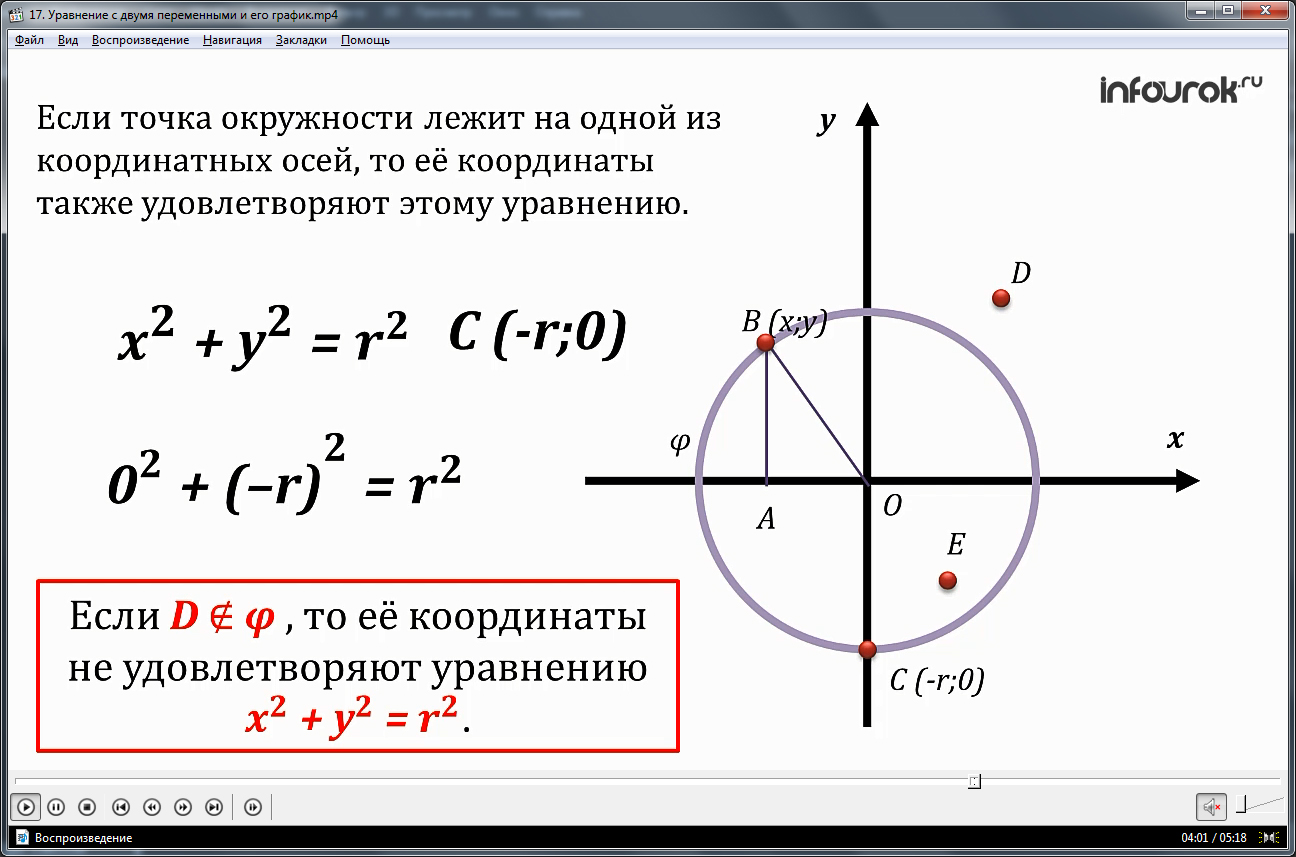
Ученикам демонстрируется построение графика функции x 2 +y 2 =r 2 , где r – произвольное положительное число. Окружность, являющаяся графиком данного уравнения, представлена на экране. Доказывается, что любая точка окружности будет удовлетворять данному уравнению. Для этого отмечаем произвольную точку В(х;у). Длина опущенного на ось абсцисс перпендикуляра равна модулю ординаты данной точки, а отрезок, проведенный из данной точки в начало координат – радиусу. Длина отрезка от начала координат до точки пересечения перпендикуляра с осью абсцисс равна модулю абсциссы. Из полученного прямоугольного треугольника АОВ имеем равенство: АО 2 +АВ 2 =ВО 2 , то есть |x| 2 +|y| 2 =r 2 . Это равенство также справедливо без знака модуля.

Чтобы убедиться, что уравнение верно в любом положении В(х;у) на окружности, предлагается рассмотреть точку В, которая лежит в точке пересечения окружности с осью абсцисс. Отмечается, что в этом случае одна координата точкиу равняется радиусу, а вторая – нуль. Уравнение x 2 +y 2 =r 2 превращается в 0 2 +r 2 =r 2 , поэтому равенство также справедливо. При этом для всех точек, которые не лежат в области определения, их координаты не удовлетворяют уравнению окружности x 2 +y 2 =r 2 . Примеры таких точек отмечены на координатной плоскости. Общий вывод из рассмотренного построения следует, что уравнение окружности в записи х 2 +у 2 =r 2 верно для случаев, когда точки А(х;у) принадлежат области определения φ, О(0;0) – центр окружности, а r — радиус.

Далее рассматривается, как уравнение окружности зависит от положения ее центра. Отмечается, что при переносе центра на |а| единиц вправо или влево параллельно х, а также на |b| единиц вверх или вниз, параллельно у, получается окружность того же радиуса, только с центром в точке с новыми координатами О(a;b). Уравнением такой окружности будет (x-a) 2 +(y-b) 2 =r 2 .

Видеоурок «Уравнение с двумя переменными и его график» может быть использован как наглядное пособие на уроке алгебры по данной теме или заменить объяснение учителя по теме. Также данный материал может быть полезен при дистанционном обучении, поможет освоить тему ученикам самостоятельно.