Графики и уравнения основных элементарных функций

Основные элементарные функции: их свойства и графики

Основные элементарные функции, присущие им свойства и соответствующие графики – одни из азов математических знаний, схожих по степени важности с таблицей умножения. Элементарные функции являются базой, опорой для изучения всех теоретических вопросов.

Статья ниже дает ключевой материал по теме основных элементарных функций. Мы введем термины, дадим им определения; подробно изучим каждый вид элементарных функций, разберем их свойства.

Выделяют следующие виды основных элементарных функций:

постоянная функция (константа);
корень n -ой степени;
степенная функция;
показательная функция;
логарифмическая функция;
тригонометрические функции;
братные тригонометрические функции.

Постоянная функция

Постоянная функция определяется формулой: y = C ( C – некое действительное число) и имеет также название: константа. Данная функция определяет соответствие любому действительному значению независимой переменной x одного и того же значения переменной y – значение C .

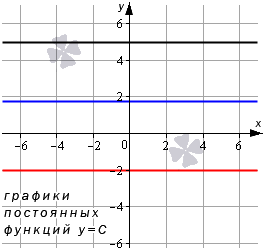
График константы – это прямая, которая параллельна оси абсцисс и проходит через точку, имеющую координаты ( 0 , С ) . Для наглядности приведем графики постоянных функций y = 5 , y = — 2 , y = 3 , y = 3 (на чертеже обозначено черным, красным и синим цветами соответственно).

Свойства постоянных функций:

область определения – все множество действительных чисел;
постоянная функция – четная;
область значений – множество, составленное из единственного числа C ;
постоянная функция является невозрастающей и неубывающей;
постоянная функция – прямая линия, о выпуклости или вогнутости здесь речи быть не может;
асимптоты отсутствуют;
точка прохождения функции на координатной плоскости – ( 0 ; С ) .

Корень n-й степени

Данная элементарная функция определяется формулой y = x n ( n – натуральное число больше единицы).

Рассмотрим две вариации функции.

Корень n -й степени, n – четное число

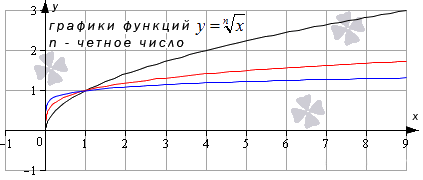
Для наглядности укажем чертеж , на котором изображены графики таких функций: y = x , y = x 4 и y = x 8 . Эти функции отмечены цветом: черный, красный и синий соответственно.

Похожий вид у графиков функции четной степени при иных значениях показателя.

Свойства функции корень n-ой степени, n – четное число

область определения – множество всех неотрицательных действительных чисел [ 0 , + ∞ ) ;
когда x = 0 , функция y = x n имеет значение, равное нулю;
данная функция- функция общего вида (не является ни четной, ни нечетной);
область значений: [ 0 , + ∞ ) ;
данная функция y = x n при четных показателях корня возрастает на всей области определения;
функция обладает выпуклостью с направлением вверх на всей области определения;
отсутствуют точки перегиба;
асимптоты отсутствуют;
график функции при четных n проходит через точки ( 0 ; 0 ) и ( 1 ; 1 ) .

Корень n -й степени, n – нечетное число

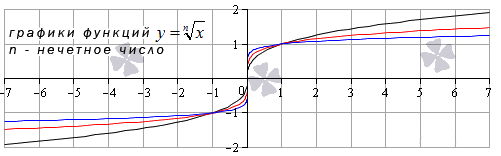
Такая функция определена на всем множестве действительных чисел. Для наглядности рассмотрим графики функций y = x 3 , y = x 5 и x 9 . На чертеже они обозначены цветами: черный, красный и синий цвета кривых соответственно.

Иные нечетные значения показателя корня функции y = x n дадут график аналогичного вида.

Свойства функции корень n-ой степени, n – нечетное число

область определения – множество всех действительных чисел;
данная функция – нечетная;
область значений – множество всех действительных чисел;
функция y = x n при нечетных показателях корня возрастает на всей области определения;
функция имеет вогнутость на промежутке ( — ∞ ; 0 ] и выпуклость на промежутке [ 0 , + ∞ ) ;
точка перегиба имеет координаты ( 0 ; 0 ) ;
асимптоты отсутствуют;
график функции при нечетных n проходит через точки ( — 1 ; — 1 ) , ( 0 ; 0 ) и ( 1 ; 1 ) .

Степенная функция

Степенная функция определяется формулой y = x a .

Вид графиков и свойства функции зависят от значения показателя степени.

когда степенная функция имеет целый показатель a , то вид графика степенной функции и ее свойства зависят от того, четный или нечетный показатель степени, а также того, какой знак имеет показатель степени. Рассмотрим все эти частные случаи подробнее ниже;
показатель степени может быть дробным или иррациональным – в зависимости от этого также варьируется вид графиков и свойства функции. Мы разберем частные случаи, задав несколько условий: 0 a 1 ; a > 1 ; — 1 a 0 и a — 1 ;
степенная функция может иметь нулевой показатель, этот случай также ниже разберем подробнее.

Степенная функция при нечетном положительном показателе

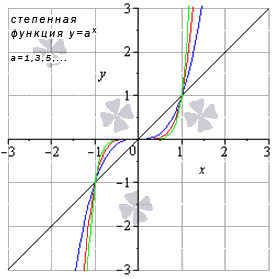
Разберем степенную функцию y = x a , когда a – нечетное положительное число, например, a = 1 , 3 , 5 …

Для наглядности укажем графики таких степенных функций: y = x (черный цвет графика), y = x 3 (синий цвет графика), y = x 5 (красный цвет графика), y = x 7 (зеленый цвет графика). Когда a = 1 , получаем линейную функцию y = x .

Свойства степенной функции, когда показатель степени – нечетный положительный

область определения: x ∈ — ∞ ; + ∞ ;
область значений: y ∈ — ∞ ; + ∞ ;
функция является нечетной, поскольку y ( — x ) = — y ( x ) ;
функция является возрастающей при x ∈ ( — ∞ ; + ∞ ) ;
функция имеет выпуклость при x ∈ ( — ∞ ; 0 ] и вогнутость при x ∈ [ 0 ; + ∞ ) (исключая линейную функцию);
точка перегиба имеет координаты ( 0 ; 0 ) (исключая линейную функцию);
асимптоты отсутствуют;
точки прохождения функции: ( — 1 ; — 1 ) , ( 0 ; 0 ) , ( 1 ; 1 ) .

Степенная функция при четном положительном показателе

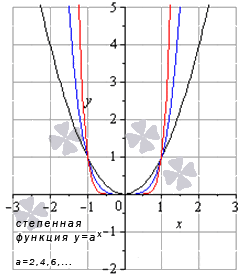
Разберем степенную функцию y = x a , когда a – четное положительное число, например, a = 2 , 4 , 6 …

Для наглядности укажем графики таких степенных функций: y = x 2 (черный цвет графика), y = x 4 (синий цвет графика), y = x 8 (красный цвет графика). Когда a = 2 , получаем квадратичную функцию, график которой – квадратичная парабола.

Свойства степенной функции, когда показатель степени – четный положительный:

область определения: x ∈ ( — ∞ ; + ∞ ) ;
область значений: y ∈ [ 0 ; + ∞ ) ;
функция является четной, поскольку y ( — x ) = y ( x ) ;
функция является возрастающей при x ∈ [ 0 ; + ∞ ) ; убывающей при x ∈ ( — ∞ ; 0 ] ;
функция имеет вогнутость при x ∈ ( — ∞ ; + ∞ ) ;
очки перегиба отсутствуют;
асимптоты отсутствуют;
точки прохождения функции: ( — 1 ; 1 ) , ( 0 ; 0 ) , ( 1 ; 1 ) .

Степенная функция при нечетном отрицательном показателе

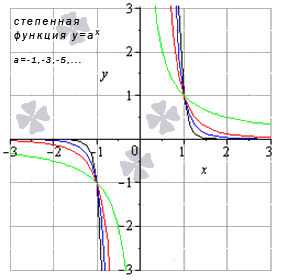
На рисунке ниже приведены примеры графиков степенной функции y = x a , когда a – нечетное отрицательное число: y = x — 9 (черный цвет графика); y = x — 5 (синий цвет графика); y = x — 3 (красный цвет графика); y = x — 1 (зеленый цвет графика). Когда a = — 1 , получаем обратную пропорциональность, график которой – гипербола.

Свойства степенной функции, когда показатель степени – нечетный отрицательный:

область определения: x ∈ ( — ∞ ; 0 ) ∪ ( 0 ; + ∞ ) ;

Когда х = 0 , получаем разрыв второго рода, поскольку lim x → 0 — 0 x a = — ∞ , lim x → 0 + 0 x a = + ∞ при a = — 1 , — 3 , — 5 , … . Таким образом, прямая х = 0 – вертикальная асимптота;

область значений: y ∈ ( — ∞ ; 0 ) ∪ ( 0 ; + ∞ ) ;
функция является нечетной, поскольку y ( — x ) = — y ( x ) ;
функция является убывающей при x ∈ — ∞ ; 0 ∪ ( 0 ; + ∞ ) ;
функция имеет выпуклость при x ∈ ( — ∞ ; 0 ) и вогнутость при x ∈ ( 0 ; + ∞ ) ;
точки перегиба отсутствуют;
горизонтальная асимптота – прямая y = 0 , поскольку:

k = lim x → ∞ x a x = 0 , b = lim x → ∞ ( x a — k x ) = 0 ⇒ y = k x + b = 0 , когда а = — 1 , — 3 , — 5 , . . . .

точки прохождения функции: ( — 1 ; — 1 ) , ( 1 ; 1 ) .

Степенная функция при четном отрицательном показателе степени

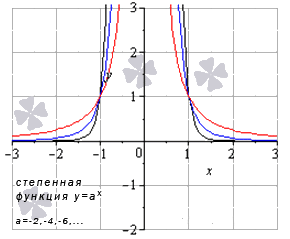
На рисунке ниже приведены примеры графиков степенной функции y = x a , когда a – четное отрицательное число: y = x — 8 (черный цвет графика); y = x — 4 (синий цвет графика); y = x — 2 (красный цвет графика).

Свойства степенной функции, когда показатель степени – четный отрицательный:

область определения: x ∈ ( — ∞ ; 0 ) ∪ ( 0 ; + ∞ ) ;

Когда х = 0 , получаем разрыв второго рода, поскольку lim x → 0 — 0 x a = + ∞ , lim x → 0 + 0 x a = + ∞ при a = — 2 , — 4 , — 6 , … . Таким образом, прямая х = 0 – вертикальная асимптота;

область значений: y ∈ ( 0 ; + ∞ ) ;
функция является четной, поскольку y ( — x ) = y ( x ) ;
функция является возрастающей при x ∈ ( — ∞ ; 0 ) и убывающей при x ∈ 0 ; + ∞ ;
функция имеет вогнутость при x ∈ ( — ∞ ; 0 ) ∪ ( 0 ; + ∞ ) ;
точки перегиба отсутствуют;
горизонтальная асимптота – прямая y = 0 , поскольку:

k = lim x → ∞ x a x = 0 , b = lim x → ∞ ( x a — k x ) = 0 ⇒ y = k x + b = 0 , когда a = — 2 , — 4 , — 6 , . . . .

точки прохождения функции: ( — 1 ; 1 ) , ( 1 ; 1 ) .

Степенная функция при рациональном или иррациональном показателе (значение больше нуля и меньше единицы)

С самого начала обратите внимание на следующий аспект: в случае, когда a – положительная дробь с нечетным знаменателем, некоторые авторы принимают за область определения этой степенной функции интервал — ∞ ; + ∞ , оговаривая при этом, что показатель a – несократимая дробь. На данный момент авторы многих учебных изданий по алгебре и началам анализа НЕ ОПРЕДЕЛЯЮТ степенные функции, где показатель – дробь с нечетным знаменателем при отрицательных значениях аргумента. Далее мы придержемся именно такой позиции: возьмем за область определения степенных функций с дробными положительными показателями степени множество [ 0 ; + ∞ ) . Рекомендация для учащихся: выяснить взгляд преподавателя на этот момент во избежание разногласий.

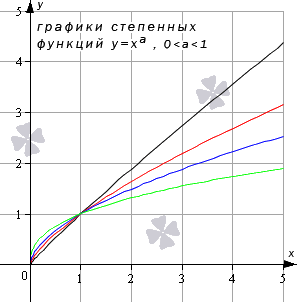
Итак, разберем степенную функцию y = x a , когда показатель степени – рациональное или иррациональное число при условии, что 0 a 1 .

Проиллюстрируем графиками степенные функции y = x a , когда a = 11 12 (черный цвет графика); a = 5 7 (красный цвет графика); a = 1 3 (синий цвет графика); a = 2 5 (зеленый цвет графика).

Иные значения показателя степени a (при условии 0 a 1 ) дадут аналогичный вид графика.

Свойства степенной функции при 0 a 1 :

область определения: x ∈ [ 0 ; + ∞ ) ;
область значений: y ∈ [ 0 ; + ∞ ) ;
данная функция – функция общего вида (не является ни нечетной, ни четной);
функция является возрастающей при x ∈ [ 0 ; + ∞ ) ;
функция имеет выпуклость при x ∈ ( 0 ; + ∞ ) ;
точки перегиба отсутствуют;
асимптоты отсутствуют;
точки прохождения функции: ( 0 ; 0 ) , ( 1 ; 1 ) .

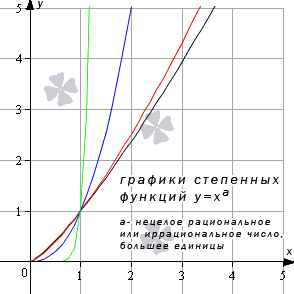
Степенная функция при нецелом рациональном или иррациональном показателе степени (больше единицы)

Разберем степенную функцию y = x a , когда показатель степени – нецелое рациональное или иррациональное число при условии, что a > 1 .

Проиллюстрируем графиками степенную функцию y = x a в заданных условиях на примере таких функций: y = x 5 4 , y = x 4 3 , y = x 7 3 , y = x 3 π (черный, красный, синий, зеленый цвет графиков соответственно).

Иные значения показателя степени а при условии a > 1 дадут похожий вид графика.

Свойства степенной функции при a > 1 :

область определения: x ∈ [ 0 ; + ∞ ) ;
область значений: y ∈ [ 0 ; + ∞ ) ;
данная функция – функция общего вида (не является ни нечетной, ни четной);
функция является возрастающей при x ∈ [ 0 ; + ∞ ) ;
функция имеет вогнутость при x ∈ ( 0 ; + ∞ ) (когда 1 a 2 ) и выпуклость при x ∈ [ 0 ; + ∞ ) (когда a > 2 );
точки перегиба отсутствуют;
асимптоты отсутствуют;
точки прохождения функции: ( 0 ; 0 ) , ( 1 ; 1 ) .

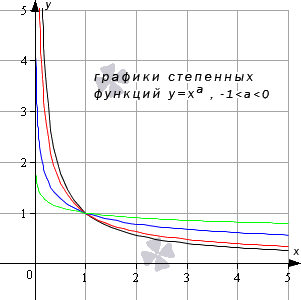
Степенная функция при действительном показателе степени (больше минус единицы и меньше нуля)

Обращаем ваше внимание! Когда a – отрицательная дробь с нечетным знаменателем, в работах некоторых авторов встречается взгляд, что область определения в данном случае – интервал — ∞ ; 0 ∪ ( 0 ; + ∞ ) с оговоркой, что показатель степени a – несократимая дробь. На данный момент авторы учебных материалов по алгебре и началам анализа НЕ ОПРЕДЕЛЯЮТ степенные функции с показателем в виде дроби с нечетным знаменателем при отрицательных значениях аргумента. Далее мы придерживаемся именно такого взгляда: возьмем за область определения степенных функций с дробными отрицательными показателями множество ( 0 ; + ∞ ) . Рекомендация для учащихся: уточните видение вашего преподавателя на этот момент во избежание разногласий.

Продолжаем тему и разбираем степенную функцию y = x a при условии: — 1 a 0 .

Приведем чертеж графиков следующий функций: y = x — 5 6 , y = x — 2 3 , y = x — 1 2 2 , y = x — 1 7 (черный, красный, синий, зеленый цвет линий соответственно).

Свойства степенной функции при — 1 a 0 :

lim x → 0 + 0 x a = + ∞ , когда — 1 a 0 , т.е. х = 0 – вертикальная асимптота;

область значений: y ∈ 0 ; + ∞ ;
данная функция – функция общего вида (не является ни нечетной, ни четной);
функция является убывающей при x ∈ 0 ; + ∞ ;
функция имеет вогнутость при x ∈ 0 ; + ∞ ;
точки перегиба отсутствуют;
горизонтальная асимптота – прямая y = 0 ;
точка прохождения функции: ( 1 ; 1 ) .

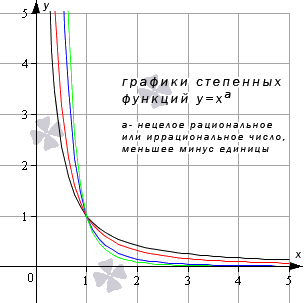
Степенная функция при нецелом действительном показателе степени (меньше минус единицы)

На чертеже ниже приведены графики степенных функций y = x — 5 4 , y = x — 5 3 , y = x — 6 , y = x — 24 7 (черный, красный, синий, зеленый цвета кривых соответственно).

Свойства степенной функции при a — 1 :

lim x → 0 + 0 x a = + ∞ , когда a — 1 , т.е. х = 0 – вертикальная асимптота;

область значений: y ∈ ( 0 ; + ∞ ) ;
данная функция – функция общего вида (не является ни нечетной, ни четной);
функция является убывающей при x ∈ 0 ; + ∞ ;
функция имеет вогнутость при x ∈ 0 ; + ∞ ;
точки перегиба отсутствуют;
горизонтальная асимптота – прямая y = 0 ;
точка прохождения функции: ( 1 ; 1 ) .

Когда a = 0 и х ≠ 0 , получим функцию y = x 0 = 1 , определяющую прямую, из которой исключена точка ( 0 ; 1 ) (условились, что выражению 0 0 не будет придаваться никакого значения).

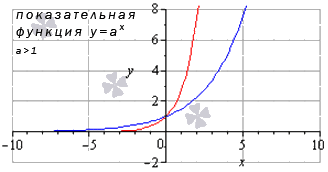
Показательная функция

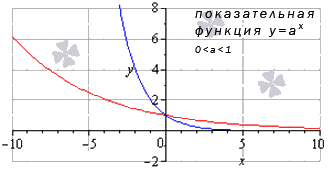
Показательная функция имеет вид y = a x , где а > 0 и а ≠ 1 , и график этой функции выглядит различно, исходя из значения основания a . Рассмотрим частные случаи.

Сначала разберем ситуацию, когда основание показательной функции имеет значение от нуля до единицы ( 0 a 1 ) . Наглядным примером послужат графики функций при a = 1 2 (синий цвет кривой) и a = 5 6 (красный цвет кривой).

Подобный же вид будут иметь графики показательной функции при иных значениях основания при условии 0 a 1 .

Свойства показательной функции, когда основание меньше единицы:

область определения – все множество действительных чисел;
область значений: y ∈ ( 0 ; + ∞ ) ;
данная функция – функция общего вида (не является ни нечетной, ни четной);
показательная функция, у которой основание меньше единицы, является убывающей на всей области определения;
функция имеет вогнутость при x ∈ — ∞ ; + ∞ ;
точки перегиба отсутствуют;
горизонтальная асимптота – прямая y = 0 при переменной x , стремящейся к + ∞ ;
точка прохождения функции: ( 0 ; 1 ) .

Теперь рассмотрим случай, когда основание показательной функции больше, чем единица ( а > 1 ) .

Проиллюстрируем этот частный случай графиком показательных функций y = 3 2 x (синий цвет кривой) и y = e x (красный цвет графика).

Иные значения основания, большие единицы, дадут аналогичный вид графика показательной функции.

Свойства показательной функции, когда основание больше единицы:

область определения – все множество действительных чисел;
область значений: y ∈ ( 0 ; + ∞ ) ;
данная функция – функция общего вида (не является ни нечетной, ни четной);
показательная функция, у которой основание больше единицы, является возрастающей при x ∈ — ∞ ; + ∞ ;
функция имеет вогнутость при x ∈ — ∞ ; + ∞ ;
точки перегиба отсутствуют;
горизонтальная асимптота – прямая y = 0 при переменной x , стремящейся к — ∞ ;
точка прохождения функции: ( 0 ; 1 ) .

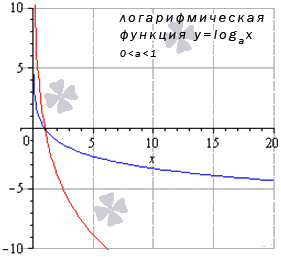
Логарифмическая функция

Логарифмическая функция имеет вид y = log a ( x ) , где a > 0 , a ≠ 1 .

Такая функция определена только при положительных значениях аргумента: при x ∈ 0 ; + ∞ .

График логарифмической функции имеет различный вид, исходя из значения основания а.

Рассмотрим сначала ситуацию, когда 0 a 1 . Продемонстрируем этот частный случай графиком логарифмической функции при a = 1 2 (синий цвет кривой) и а = 5 6 (красный цвет кривой).

Иные значения основания, не большие единицы, дадут аналогичный вид графика.

Свойства логарифмической функции, когда основание меньше единицы:

область определения: x ∈ 0 ; + ∞ . Когда х стремится к нулю справа, значения функции стремятся к + ∞ ;
область значений: y ∈ — ∞ ; + ∞ ;
данная функция – функция общего вида (не является ни нечетной, ни четной);
логарифмическая функция является убывающей на всей области определения;
функция имеет вогнутость при x ∈ 0 ; + ∞ ;
точки перегиба отсутствуют;
асимптоты отсутствуют;
точка прохождения функции: ( 1 ; 0 ) .

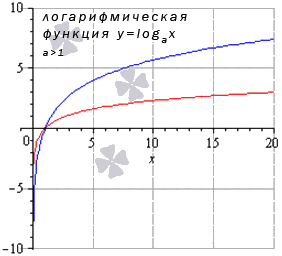
Теперь разберем частный случай, когда основание логарифмической функции больше единицы: а > 1 . На чертеже ниже – графики логарифмических функций y = log 3 2 x и y = ln x (синий и красный цвета графиков соответственно).

Иные значения основания больше единицы дадут аналогичный вид графика.

Свойства логарифмической функции, когда основание больше единицы:

область определения: x ∈ 0 ; + ∞ . Когда х стремится к нулю справа, значения функции стремятся к — ∞ ;
область значений: y ∈ — ∞ ; + ∞ (все множество действительных чисел);
данная функция – функция общего вида (не является ни нечетной, ни четной);
логарифмическая функция является возрастающей при x ∈ 0 ; + ∞ ;
функция имеет выпуклость при x ∈ 0 ; + ∞ ;
точки перегиба отсутствуют;
асимптоты отсутствуют;
точка прохождения функции: ( 1 ; 0 ) .

Тригонометрические функции, их свойства и графики

Тригонометрические функции – это синус, косинус, тангенс и котангенс. Разберем свойства каждой из них и соответствующие графики.

В общем для всех тригонометрических функций характерно свойство периодичности, т.е. когда значения функций повторяются при разных значениях аргумента, отличающихся друг от друга на величину периода f ( x + T ) = f ( x ) ( T – период). Таким образом, в списке свойств тригонометрических функций добавляется пункт «наименьший положительный период». Помимо этого, будем указывать такие значения аргумента, при которых соответствующая функция обращается в нуль.

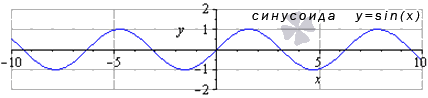
Функция синус: y = sin ( х )

График данной функции называется синусоида.

Свойства функции синус:

область определения: все множество действительных чисел x ∈ — ∞ ; + ∞ ;
наименьший положительный период: Т = 2 π ;
функция обращается в нуль, когда x = π · k , где k ∈ Z ( Z – множество целых чисел);
область значений: y ∈ — 1 ; 1 ;
данная функция – нечетная, поскольку y ( — x ) = — y ( x ) ;
функция является возрастающей при x ∈ — π 2 + 2 π · k ; π 2 + 2 π · k , k ∈ Z и убывающей при x ∈ π 2 + 2 π · k ; 3 π 2 + 2 π · k , k ∈ Z ;
функция синус имеет локальные максимумы в точках π 2 + 2 π · k ; 1 и локальные минимумы в точках — π 2 + 2 π · k ; — 1 , k ∈ Z ;
функция синус вогнутая, когда x ∈ — π + 2 π · k ; 2 π · k , k ∈ Z и выпуклая, когда x ∈ 2 π · k ; π + 2 π · k , k ∈ Z ;
точки перегиба имеют координаты π · k ; 0 , k ∈ Z ;
асимптоты отсутствуют.

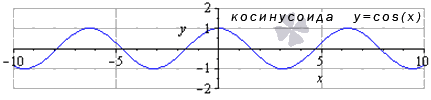
Функция косинус: y = cos ( х )

График данной функции называется косинусоида.

Свойства функции косинус:

область определения: x ∈ — ∞ ; + ∞ ;
наименьший положительный период: Т = 2 π ;
функция обращается в нуль, когда x = π 2 + π · k при k ∈ Z ( Z – множество целых чисел);
область значений: y ∈ — 1 ; 1 ;
данная функция – четная, поскольку y ( — x ) = y ( x ) ;
функция является возрастающей при x ∈ — π + 2 π · k ; 2 π · k , k ∈ Z и убывающей при x ∈ 2 π · k ; π + 2 π · k , k ∈ Z ;
функция косинус имеет локальные максимумы в точках 2 π · k ; 1 , k ∈ Z и локальные минимумы в точках π + 2 π · k ; — 1 , k ∈ z ;
функция косинус вогнутая, когда x ∈ π 2 + 2 π · k ; 3 π 2 + 2 π · k , k ∈ Z и выпуклая, когда x ∈ — π 2 + 2 π · k ; π 2 + 2 π · k , k ∈ Z ;
точки перегиба имеют координаты π 2 + π · k ; 0 , k ∈ Z
асимптоты отсутствуют.

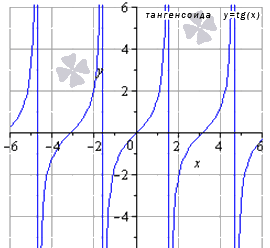
Функция тангенс: y = t g ( х )

График данной функции называется тангенсоида.

Свойства функции тангенс:

область определения: x ∈ — π 2 + π · k ; π 2 + π · k , где k ∈ Z ( Z – множество целых чисел);
Поведение функции тангенс на границе области определения lim x → π 2 + π · k + 0 t g ( x ) = — ∞ , lim x → π 2 + π · k — 0 t g ( x ) = + ∞ . Таким образом, прямые x = π 2 + π · k k ∈ Z – вертикальные асимптоты;
наименьший положительный период: Т = π ;
функция обращается в нуль, когда x = π · k при k ∈ Z ( Z – множество целых чисел);
область значений: y ∈ — ∞ ; + ∞ ;
данная функция – нечетная, поскольку y ( — x ) = — y ( x ) ;
функция является возрастающей при — π 2 + π · k ; π 2 + π · k , k ∈ Z ;
функция тангенс является вогнутой при x ∈ [ π · k ; π 2 + π · k ) , k ∈ Z и выпуклой при x ∈ ( — π 2 + π · k ; π · k ] , k ∈ Z ;
точки перегиба имеют координаты π · k ; 0 , k ∈ Z ;
наклонные и горизонтальные асимптоты отсутствуют.

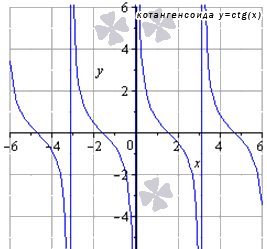
Функция котангенс: y = c t g ( х )

График данной функции называется котангенсоида.

Свойства функции котангенс:

область определения: x ∈ ( π · k ; π + π · k ) , где k ∈ Z ( Z – множество целых чисел);

Поведение функции котангенс на границе области определения lim x → π · k + 0 t g ( x ) = + ∞ , lim x → π · k — 0 t g ( x ) = — ∞ . Таким образом, прямые x = π · k k ∈ Z – вертикальные асимптоты;

наименьший положительный период: Т = π ;
функция обращается в нуль, когда x = π 2 + π · k при k ∈ Z ( Z – множество целых чисел);
область значений: y ∈ — ∞ ; + ∞ ;
данная функция – нечетная, поскольку y ( — x ) = — y ( x ) ;
функция является убывающей при x ∈ π · k ; π + π · k , k ∈ Z ;
функция котангенс является вогнутой при x ∈ ( π · k ; π 2 + π · k ] , k ∈ Z и выпуклой при x ∈ [ — π 2 + π · k ; π · k ) , k ∈ Z ;
точки перегиба имеют координаты π 2 + π · k ; 0 , k ∈ Z ;
наклонные и горизонтальные асимптоты отсутствуют.

Обратные тригонометрические функции, их свойства и графики

Обратные тригонометрические функции – это арксинус, арккосинус, арктангенс и арккотангенс. Зачастую, в связи с наличием приставки «арк» в названии, обратные тригонометрические функции называют аркфункциями.

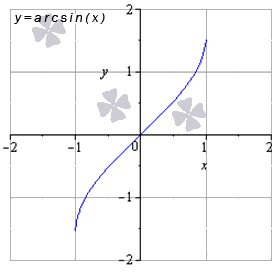
Функция арксинус: y = a r c sin ( х )

Свойства функции арксинус:

область определения: x ∈ — 1 ; 1 ;
область значений: y ∈ — π 2 ; π 2 ;
данная функция – нечетная, поскольку y ( — x ) = — y ( x ) ;
функция является возрастающей на всей области определения;
функция арксинус имеет вогнутость при x ∈ 0 ; 1 и выпуклость при x ∈ — 1 ; 0 ;
точки перегиба имеют координаты ( 0 ; 0 ) , она же – нуль функции;
асимптоты отсутствуют.

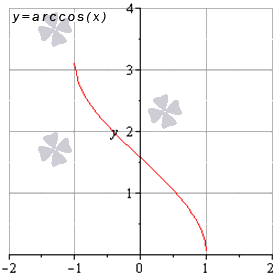
Функция арккосинус: y = a r c cos ( х )

Свойства функции арккосинус:

область определения: x ∈ — 1 ; 1 ;
область значений: y ∈ 0 ; π ;
данная функция — общего вида (ни четная, ни нечетная);
функция является убывающей на всей области определения;
функция арккосинус имеет вогнутость при x ∈ — 1 ; 0 и выпуклость при x ∈ 0 ; 1 ;
точки перегиба имеют координаты 0 ; π 2 ;
асимптоты отсутствуют.

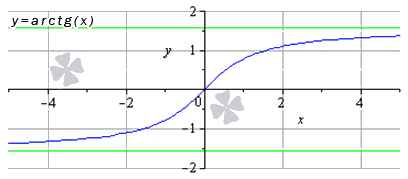
Функция арктангенс: y = a r c t g ( х )

Свойства функции арктангенс:

область определения: x ∈ — ∞ ; + ∞ ;
область значений: y ∈ — π 2 ; π 2 ;
данная функция – нечетная, поскольку y ( — x ) = — y ( x ) ;
функция является возрастающей на всей области определения;
функция арктангенс имеет вогнутость при x ∈ ( — ∞ ; 0 ] и выпуклость при x ∈ [ 0 ; + ∞ ) ;
точка перегиба имеет координаты ( 0 ; 0 ) , она же – нуль функции;
горизонтальные асимптоты – прямые y = — π 2 при x → — ∞ и y = π 2 при x → + ∞ (на рисунке асимптоты – это линии зеленого цвета).

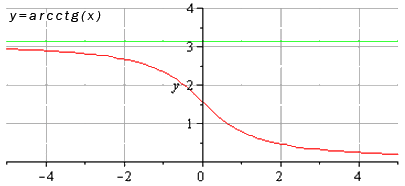
Функция арккотангенс: y = a r c c t g ( х )

Свойства функции арккотангенс:

область определения: x ∈ — ∞ ; + ∞ ;
область значений: y ∈ ( 0 ; π ) ;
данная функция – общего вида;
функция является убывающей на всей области определения;
функция арккотангенс имеет вогнутость при x ∈ [ 0 ; + ∞ ) и выпуклость при x ∈ ( — ∞ ; 0 ] ;
точка перегиба имеет координаты 0 ; π 2 ;
горизонтальные асимптоты – прямые y = π при x → — ∞ (на чертеже – линия зеленого цвета) и y = 0 при x → + ∞ .

Элементарные функции и их графики

Понятие функции — одно из ключевых в математике. О нём подробно рассказано в статье «Что такое функция».

И конечно, в задачах части 2 Профильного ЕГЭ по математике без них не обойтись. А если вы выбрали технический или экономический вуз — первая же лекция по матанализу будет посвящена именно элементарным функциями и их графикам.

Но это не всё. Математические функции, изучением которых мы занимаемся, — это не что-то такое выдуманное или существующее только в замкнутом пространстве учебника. Они являются отражением реальных взаимосвязей и процессов, происходящих в природе и обществе.

Существует всего пять типов элементарных функций:

1. Степенные
К этому типу относятся линейные, квадратичные, кубические, , , Все они содержат выражения вида x α .

2. Показательные
Это функции вида y = a x

4. Тригонометрические
В их формулах присутствуют синусы, косинусы, тангенсы и котангенсы.

Элементарными они называются потому, что из них, как из элементов, получаются все остальные, встречающиеся в школьном курсе. Например, y = x 2 · e x — произведение квадратичной и показательной функций; y = sin(a x ) — сложная функция, то есть комбинация двух функций — показательной и тригонометрической.

Графики и свойства основных элементарных функций следует знать наизусть.

1. Линейная функция y = x

2. Квадратичная парабола y = x 2

3. Функция y = x n ,
n — натуральное, n > 1
n — чётное
n = 2, 4, 6.

n — нечётное
n = 3, 5, 7.

4.Гипербола

Показательная функция y = a x

a > 1

0 1

0 2 + 5? Об этом — статья «Преобразования графиков функций».

Обратите внимание: уравнения, которые вы решаете, обычно относятся к одному из этих пяти типов. Для каждого типа — свои способы решения. Это и понятно: они основаны на тех или иных свойствах функций.

Почему в уравнении 3 x = 3 5 мы можем «отбросить» основания и записать, что x = 5? Да потому что показательная функция y = 3 x возрастает и каждое значение принимает только один раз.

Почему уравнение имеет бесконечно много решений, которые записываются в виде серии: , где n — целое? Потому что функция y = sinx — периодическая, то есть каждое свое значение принимает бесконечно много раз.

Зная графики элементарных функций, вы уже не запутаетесь с ОДЗ уравнений и неравенств. Вы сможете решать сложные задачи графически — а это часто во много раз легче и быстрее, чем аналитически.

Есть еще и такие уравнения, где слева и справа стоят функции разных типов. Для их решения есть графический способ, а также специальные приемы, о которых рассказывается в статье «Метод оценки».

Построение графиков функций

О чем эта статья:

11 класс, ЕГЭ/ОГЭ

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Понятие функции

Функция — это зависимость y от x, где x является переменной или аргументом функции, а y — зависимой переменной или значением функции.

Задать функцию значит определить правило, в соответствии с которым по значениям независимой переменной можно найти соответствующие ее значения. Вот, какими способами ее можно задать:

Табличный способ — помогает быстро определить конкретные значения без дополнительных измерений или вычислений.
Графический способ — наглядно.
Аналитический способ — через формулы. Компактно, и можно посчитать функцию при произвольном значении аргумента из области определения.
Словесный способ.

Область определения — множество х, то есть область допустимых значений выражения, которое записано в формуле.

Например, для функции вида область определения выглядит так

х ≠ 0, потому что на ноль делить нельзя. Записать можно так: D (y): х ≠ 0.

Область значений — множество у, то есть это значения, которые может принимать функция.

Например, естественная область значений функции y = x² — это все числа больше либо равные нулю. Можно записать вот так: Е (у): у ≥ 0.

Понятие графика функции

Графиком функции y = f(x) называется множество точек (x; y), координаты которых связаны соотношением y = f(x). Само равенство y = f(x) называется уравнением данного графика.

График функции — это множество точек (x; y), где x — это аргумент, а y — значение функции, которое соответствует данному аргументу.

Проще говоря, график функции показывает множество всех точек, координаты которых можно найти, просто подставив в функцию любые числа вместо x.

Для примера возьмём самую простую функцию, в которой аргумент равен значению функции, то есть y = x.

В этом случае нам не придётся вычислять для каждого аргумента значение функции, так как они равны, поэтому у всех точек нашего графика абсцисса будет равна ординате.

Отметим любые три точки на координатной плоскости, например: L (-2; -2), M (0; 0) и N (1; 1).

Если мы последовательно от наименьшего значения аргумента к большему соединим отмеченные точки, то у нас получится прямая линия. Значит графиком функции y = x является прямая. На графике это выглядит так:

Надпись на чертеже y = x — это уравнение графика. Ставить надпись с уравнением на чертеже удобно, чтобы не запутаться в решении задач.

Важно отметить, что прямая линия бесконечна в обе стороны. Хоть мы и называем часть прямой графиком функции, на самом деле на чертеже изображена только малая часть графика.

Исследование функции

Важные точки графика функции y = f(x):

стационарные и критические точки;
точки экстремума;
нули функции;
точки разрыва функции.

Стационарные точки — точки, в которых производная функции f(x) равна нулю.

Критические точки — точки, в которых производная функции f(x) равна нулю либо не существует. Стационарные точки являются подмножеством множества критических точек.

Экстремум в математике — максимальное или минимальное значение функции на заданном множестве. Точка, в которой достигается экстремум, называется точкой экстремума. Соответственно, если достигается минимум — точка экстремума называется точкой минимума, а если максимум — точкой максимума.

Нули функции — это значения аргумента, при которых функция равна нулю.

Асимптота — прямая, которая обладает таким свойством, что расстояние от точки графика функции до этой прямой стремится к нулю при неограниченном удалении точки графика от начала координат. По способам их отыскания выделяют три вида асимптот: вертикальные, горизонтальные, наклонные.

Функция непрерывна в точке k, если предел функции в данной точке равен значению функции в этой точке:

Если функция f(x) не является непрерывной в точке x = a, то говорят, что f(x) имеет разрыв в этой точке.

Если нам нужно построить график незнакомой функции, когда заранее невозможно представить вид графика, полезно применять схему исследования свойств функции. Она поможет составить представление о графике и приступить к построению по точкам.

Схема построения графика функции:

Найти область определения функции.
Найти область допустимых значений функции.
Проверить не является ли функция четной или нечетной.
Проверить не является ли функция периодической.
Найти нули функции.
Найти промежутки знакопостоянства функции, то есть промежутки, на которых она строго положительна или строго отрицательна.
Найти асимптоты графика функции.
Найти производную функции.
Найти критические точки в промежутках возрастания и убывания функции.
На основании проведенного исследования построить график функции.

У нас есть отличные курсы по математике для учеников с 1 по 11 классы!

Построение графика функции

Чтобы понять, как строить графики функций, потренируемся на примерах.

Задача 1. Построим график функции

Упростим формулу функции:

при х ≠ -1.

График функции — прямая y = x — 1 с выколотой точкой M (-1; -2).

Задача 2. Построим график функции

Выделим в формуле функции целую часть:

График функции — гипербола, сдвинутая на 3 вправо по x и на 2 вверх по y и растянутая в 10 раз по сравнению с графиком функции

Выделение целой части — полезный прием, который применяется в решении неравенств, построении графиков и оценке целых величин.

Задача 3. По виду графика определить знаки коэффициентов общего вида функции y = ax2 + bx + c.

Вспомним, как параметры a, b и c определяют положение параболы.

Ветви вниз, следовательно, a 0.

Точка пересечения с осью Oy — c = 0.

Координата вершины , т.к. неизвестное число при делении на положительное дает отрицательный результат, то это число отрицательное, следовательно, b > 0.

Ветви вниз, следовательно, a 0.

Координата вершины , т.к. неизвестное число при делении на отрицательное дает в результате положительное, то это число отрицательное, следовательно, b

x	y
0	-1
1	2

Как видим, k = 3 > 0 и угол наклона к оси Ox острый, b = -1 — смещение по оси Oy.

x	y
0	2
1	1

k = -1 > 0 и b = 2 можно сделать аналогичные выводы, как и в первом пункте.

x	y
0	0
1	2

k = 2 > 0 — угол наклона к оси Ox острый, B = 0 — график проходит через начало координат.

k = 0 — константная функция, прямая проходит через точку b = -1 и параллельно оси Ox.

Задача 5. Построить график функции

Это дробно-рациональная функция. Область определения функции D(y): x ≠ 4; x ≠ 0.

Нули функции: 3, 2, 6.

Промежутки знакопостоянства функции определим с помощью метода интервалов.

Вертикальные асимптоты: x = 0, x = 4.

Если x стремится к бесконечности, то у стремится к 1. Значит, y = 1 — горизонтальная асимптота.

Вот так выглядит график:

Задача 6. Построить графики функций:

б)

г)

д)

Когда сложная функция получена из простейшей через несколько преобразований, то преобразования графиков можно выполнить в порядке арифметических действий с аргументом.

а)

Преобразование в одно действие типа f(x) + a.

Сдвигаем график вверх на 1:

б)

Преобразование в одно действие типа f(x — a).

Сдвигаем график вправо на 1:

В этом примере два преобразования, выполним их в порядке действий: сначала действия в скобках f(x — a), затем сложение f(x) + a.

Сдвигаем график вправо на 1:

Сдвигаем график вверх на 2:

г)

Преобразование в одно действие типа

Растягиваем график в 2 раза от оси ординат вдоль оси абсцисс:

д)

Мы видим три преобразования вида f(ax), f (x + a), -f(x).

Чтобы выполнить преобразования, посмотрим на порядок действий: сначала умножаем, затем складываем, а уже потом меняем знак. Чтобы применить умножение ко всему аргументу модуля в целом, вынесем двойку за скобки в модуле.

Сжимаем график в два раза вдоль оси абсцисс:

Сдвигаем график влево на 1/2 вдоль оси абсцисс:

Отражаем график симметрично относительно оси абсцисс:

источники:

http://ege-study.ru/ru/ege/materialy/matematika/elementarnye-funkcii-i-ix-grafiki/

http://skysmart.ru/articles/mathematic/postroenie-grafikov-funkcij