Показательные функции и логарифмы в математике с примерами решения и образцами выполнения
Определение показательной функции:
Определение:
Показательной функцией от независимого переменного х называется выражение 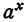
Если а положительно, функция 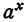
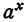
Если а отрицательно, функция 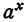
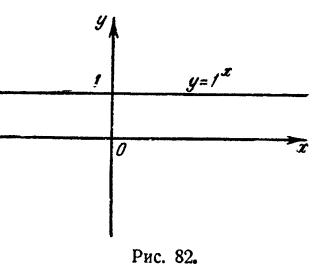
Если а = 0, функция 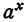
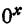
Свойства функции
- Если а > 0, функция
определена при всех значениях х от -∞ до +∞
- При всех значениях х функция
> 0
- При а > 1 функция
возрастает. При a х₂ . Тогда при
а при
Точно так же доказывается, что нельзя предполагать, что x₁ 1 то при неограниченном возрастании показателя х функция
неограниченно возрастает, а при неограниченном убывании показателя х функция
принимает значения, сколь угодно близкие к нулю.
Если a
Доказательство:
Пусть а > 1 и М—сколь угодно большое положительное число. Как показано в теореме 2 § 9 гл. V, 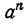
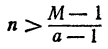
При всех значениях х, удовлетворяющих этому неравенству,
Пусть теперь m— сколь угодно малое положительное число. По доказанному найдется такое х, что 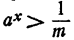
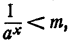
Первая часть утверждения доказана.
Пусть теперь а
убывает от значений сколь угодно больших до значений, сколь угодно близких к нулю. Вторая часть утверждения доказана.
6. Если а положительно и отлично от единицы, то каково бы ни было положительное число N, существует и притом только одно такое значение х, что
Иными словами, если а положительно и отлично от единицы и N— данное положительное число, уравнение 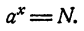
Доказательство:
Докажем сначала, что уравнение имеет решение. Одно из двух: или существует такое рациональное число г, что 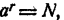
Пусть а > 1. Существует такое целое т, что 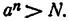

Рассмотрим последовательность степеней
Сравнивая члены последовательности (1) с числом N, можно найти такие два соседних члена 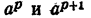
Составим теперь последовательность
Сравнивая члены последовательности (2) с числом N, можно найти таких два соседних члена 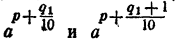
Сравнивая члены последовательности (3) с числом N, опять найдем таких два соседних члена 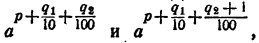
Продолжая неограниченно процесс деления промежутка на 10 равных частей и сравнивая всякий раз число N с получающимися при этом степенями числа а, получим две последовательности показателей
и две последовательности степеней
Последовательность (4) — возрастающая и ограниченная сверху любым членом последовательности (5). Последовательность (5) — убывающая и ограниченная снизу любым членом последовательности (4). Разность последовательностей (5) и (4) сходится к нулю. Следовательно, существует единственное число а, которое больше всех членов последовательности (4) и меньше всех членов последовательности (5).
Точно так же существует единственное число, которое больше всех членов последовательности (6) и меньше всех членов последовательности (7). Этим числом по построению последовательности является число N. По определению степени с иррациональным показателем, этим числом является 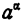
Пусть теперь а 1. Уравнение
имеет решение при любом положительном N. Это же решение удовлетворяет уравнению
Докажем, что решение единственно. Предположим, что уравнение имеет два решения: x = x₁, и х = х₂, причем x₁>x₂. Тогда имеем:
Но это невозможно, так как при
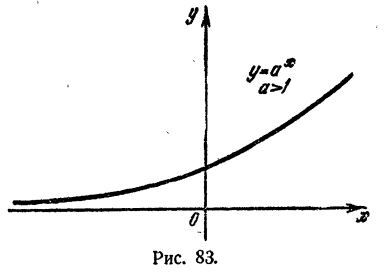
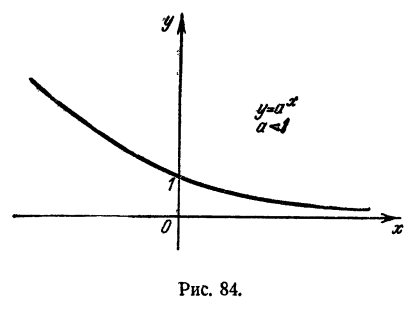
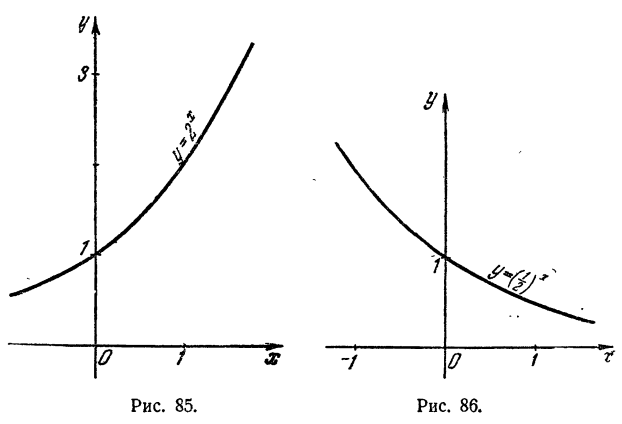
График показательной функции
Пусть а > 1, тогда график функции 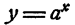
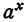
- Весь график расположен в верхней полуплоскости, т. е. там, где ординаты положительны (свойство 2 § 2).
- Всякая прямая, параллельная оси Оу, пересекает график и притом только в одной точке (свойства 1 и 4 § 2).
- Из двух точек графика правее, т. е. по мере продвижения слева направо график поднимается вверх (свойство 3 § 2).
- На графике имеются точки, лежащие выше любой прямой, параллельной оси Ох. На графике имеются точки, лежащие ниже любой прямой, проведенной в верхней полуплоскости параллельно оси Ох.
В левой своей части график, если наблюдать за ним справа налево, все ближе подходит к оси Ох, как бы стремясь коснуться ее. Однако график нигде не касается оси Ох (свойства 5 и 2 § 2).
5. Всякая прямая, параллельная оси Ох и лежащая в верхней полуплоскости, пересекает график и притом только в одной точке (свойство 6 § 2).
6. При всех а график проходит через точку (0,1). Это объясняется тем, что при любом положительном а
Если a 1 и при а
Таблица составлена посредством приближенного извлечения √2, ∜2, √8, ∜8 и т. д.
На рис. 86 изображен график функции 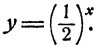
Определение логарифма
Определение:
Логарифмом числа N по основанию а называется показатель степени, в которую надо возвести а, чтобы получить N.
Для обозначения логарифма употребляется знак log. Тот факт, что число х является логарифмом числа N по основанию а, записывается так:
По определению 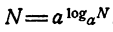
Логарифмическая функция
Пусть а > 0 и отлично от единицы. Возьмем произвольное положительное число у. Как показано (п. 6 § 2), уравнение
имеет единственное решение. Это значит, что всякое положительное число у по любому основанию (положительному и отличному от единицы) имеет единственный логарифм
Это утверждение называется теоремой о существовании логарифма.
Придавая числу у различные положительные значения, будем получать различные значения 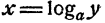
Логарифмическая функция 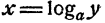
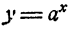
Показательная функция дает описание изменения степени числа а в зависимости от изменения показателя степени; логарифмическая функция дает описание изменения показателя степени в зависимости от изменения степени числа а.
Иными словами, показательная функция дает описание изменения числа в зависимости от изменения его логарифма по основанию а; логарифмическая функция дает описание изменения логарифма числа по основанию а в зависимости от изменения числа.
Таблица значений показательной функции при данном основании а является одновременно и таблицей значений логарифмической функции при том же основании а.
График показательной функции 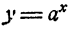
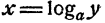
отложены на горизонтальной оси, а значения функции — на вертикальной; в другом случае, наоборот, значения функции отложены на горизонтальной оси, а значения не-, зависимого переменного — на вертикальной.
Показательная функция при основании а и логарифмическая функция при том же основании представляют пример двух обратных друг другу функций.
Обычно принято значения независимого переменного обозначать буквой х и откладывать на горизонтальной оси, а значения функции обозначать буквой у и откладывать на вертикальной оси.
Если придерживаться этого правила, то для функции 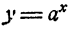
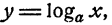
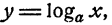
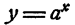
Свойства логарифмов чисел
Свойства логарифмов чисел при основании, большем единицы:
- Всякое положительное число имеет логарифм и притом только один. Это свойство вытекает из свойства 6 показательной функции.
- Отрицательные числа и число 0 не имеют логарифмов. Это свойство вытекает из свойства 2 показательной функции.
- Логарифм единицы равен нулю. Это вытекает из того, что при любом положительном а а⁰ = 1.
- Если
т. е. бoльшее число имеет и бoльший логарифм. Это вытекает из свойства 3 показательной функции.
- Логарифмы чисел, больших единицы, положительны; логарифмы чисел, меньших единицы, отрицательны. Это вытекает из свойств 3 и 4.
- Если число растет неограниченно, то и логарифм его растет неограниченно. Если число, оставаясь положительным, стремится к нулю, логарифм его становится отрицательным и сколь угодно большим по абсолютной величине.
Это свойство вытекает из свойства 5 показательной функции и условно записывается так:
7. Логарифм основания равен единице.
Свойства логарифмов чисел при положительном основании, меньшем единицы:
- Всякое положительное число имеет логарифм и притом только один.
- Отрицательные числа и число 0 не имеют логарифмов.
- Логарифм единицы равен нулю.
- Бoльшее число имеет меньший логарифм.
- Логарифмы чисел, бoльших единицы, отрицательны; логарифмы чисел, меньших единицы, положительны.
(условная запись);
(условная запись)
- Логарифм основания равен единице.
Теоремы о логарифмах
Теорема:
Логарифм произведения двух или нескольких чисел равен сумме логарифмов сомножителей.
Доказательство:
Пусть 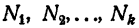
Перемножив эти равенства почленно, получим
С другой стороны, по определению логарифма,
Из равенств (1) и (2) имеем
Теорема:
Логарифм частного равен разности логарифмов делимого и делителя.
Доказательство:
Пусть N₁ и N₂ — произвольные положительные числа. По определению логарифма,
Разделив эти равенства почленно, получим
С другой стороны, по определению логарифма,
Из равенств (3) и (4) имеем:
Теорема:
Логарифм степени равен произведению показателя степени на логарифм основания.
Доказательство:
Пусть N—произвольное положительное число и а — любое вещественное число. По определению логарифма,
Возведя обе части равенства в степень а, получим
С другой стороны, по определению логарифма,
Из равенств (5) и (6) имеем
Теорема:
Логарифм корня равен логарифму подкоренного выражения, деленному на показатель корня.
Доказательство:
Пусть N — произвольное положительное число, n— натуральное. Тогда, используя теорему 3, получим
Доказанные теоремы служат основой для вычислений при помощи логарифмов.
Пусть требуется найти произведение двух чисел N₁ и N₂ Пользуясь графиком логарифмической функции или таблицей ее значений, определяют 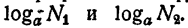
Остается по графику логарифмической функции или по таблице ее значений по 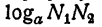
Точно так же при делении, возведении в степень и извлечении корня используются теоремы 2, 3, 4 соответственно.
Логарифмирование и потенцирование выражений
Пользуясь теоремами 1 —4 § 7, часто удается свести логарифм сложного выражения к результату простых действий над логарифмами входящих в него более простых выражений.
Такое преобразование логарифма называется логарифмированием выражения.
Например, пусть надо вычислить
Применяя теорему о логарифме частного, имеем
Далее, на основании теорем о логарифме произведения, степени и корня последовательно имеем
Таким образом, вычисление логарифма А сведено к вычислению логарифмов а, b, с, d, е.
Логарифм суммы не может быть просто выражен через логарифмы слагаемые. Иногда логарифм суммы преобразуется так:
Такое преобразование используется в так называемых гауссовых логарифмах.
При решении некоторых вопросов приходится ввести преобразование, обратное логарифмированию, т. е. приходится результат действий над логарифмами нескольких выражений преобразовывать в логарифм одного выражения. Такое преобразование логарифмов называется потенцированием выражения.
Пример:
Решение:
На основании теоремы о логарифме степени имеем:
На основании теоремы о логарифме произведения
Ha основании теоремы о логарифме частного
Так как из равенства логарифмов двух чисел дледует равенство этих чисел (см. свойство 4 § 6), то
Пример:
Найти А, если известно, что
Решение:
Ответ.
В этом параграфе, за исключением последнего примера, употребляется знак логарифма без указания основания, по которому берутся логарифмы. Объясняется это тем, что все изложенное здесь справедливо для логарифмов по любому основанию.
Десятичные логарифмы
За основание логарифмов обычно принимается число 10, так как 10 лежит в основе употребительной системы счисления. Логарифмы чисел по основанию 10 называются десятичными. Для упрощения записи десятичных логарифмов основание обычно не указывается и знак log заменяют знаком lg, т. е. вместо log₁₀N пишут lgN
Десятичные логарифмы обладают всеми свойствами логарифмов при основании, бoльшем единицы, и, кроме того, следующими:
- Если число является степенью 10 с натуральным показателем, то десятичный логарифм его равен количеству нулей в изображении этого числа. Действительно,
2. Если число является степенью числа 0,1 с натуральным показателем, то десятичный логарифм его равен целому отрицательному числу, абсолютная величина которого равна количеству нулей, входящих в десятичное изображение этого числа, в том числе и нуля целых.
Действительно, 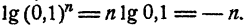
3. Если число умножить на 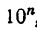
Действительно, пусть lg N = x, тогда lg
4. Если число разделить на 10ⁿ, логарифм его уменьшатся на n.
5. Если в десятичной дроби перенести запятую на п знаков вправо, логарифм ее увеличится на n. Если в десятичной дроби перенести запятую на п знаков влево, логарифм ее уменьшится на n.
6. Логарифмы рациональных чисел вообще иррациональны. Исключение составляют лишь числа, являющиеся степенью числа 10 с целым показателем.
Доказательство:
1. Пусть натуральное N имеет рациональный логарифм 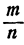
Если N делится на простое число р, отличное от 2 и 5, равенство (1) невозможно, так как 10ᵐ на р не делится. Остается предполагать, что 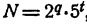
Равенство (1) принимает вид
Если m = nt равенство (2) невозможно, так как оно приводит к равенству
где q > t. Точно так же равенство (2) невозможно как при m nt. Итак,
Рассуждая точно так же, можно показать, что q не может быть меньше t.
2. Пусть N—неправильная несократимая дробь, т. е. 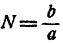
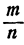
Так как степень несократимой дроби с натуральным показателем есть опять несократимая дробь, равенство (3) невозможно.
3. Пусть N — правильная несократимая дробь, т. е. 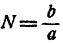
По доказанному в п. 2 равенство (4) возможно только тогда, когда b ≠ 1. Равенство (4) принимает такой вид:
По доказанному в п. 1 последнее равенство возможно только тогда, когда а есть степень числа 10 с целым неотрицательным показателем. Выходит, что
где k—целое неотрицательное число.
Характеристика и мантисса
Если действительное число не является целым, то его можно представить в виде суммы целого числа и положительного числа, меньшего единицы. Например,
Поэтому и логарифм любого положительного числа N можно представить так:
где А — целое число и 0 ≤ a
т. е. 2
где 0
т. е. —3
где 0
так как 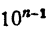
где 0 ≤ а
а — цифра, отличная от нуля. Тогда 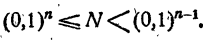
где 0 ≤ a Понятие о вычислении логарифмов
Для использования логарифмов при вычислениях необходимо, чтобы в распоряжении вычислителя имелись достаточно подробные таблицы значений логарифмической функции, вычисленные с определенной, достаточной для практических целей, точностью.
Математика располагает различными средствами для составления таких таблиц. Однако рассмотрение этих способов вычисления логарифмов выходит за пределы школьной программы.
Можно указать способ, далеко не совершенный, но весьма простой по идее, из рассмотрения которого будет видно, что логарифм любого натурального числа может быть вычислен с любой точностью.
Пусть требуется вычислить логарифм натурального числа N с точностью до 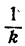
Например, 2¹⁰= 1024, значит, lg2¹⁰ = 3,… Отсюда lg2 = 0,3…
На следующем примере будет показан более совершенный способ вычисления логарифмов.
Пример:
Решение:
Обозначив искомый логарифм буквой х, имеем
Положим 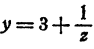
Дальнейшие вычисления по этой схеме затруднительны. Имеем
где 3
Положим z = 4, тогда
Так как 3
Посредством весьма несложных вычислений найдено значение lg2 с двумя верными знаками после запятой. Более точные вычисления показывают, что lg 2 = 0,30103 с точностью до 0,00001.
Интерполирование
Предположим, что логарифм числа N не указан в таблице. Найдем в таблице логарифмы ближайших к N чисел N₁ и N₂ из которых N₁ N Будем считать, что приращения логарифмов пропорциональны приращениям логарифмируемых чисел. Тогда имеем
откуда lgN легко определяется.
Этот способ приближенного вычисления, при котором по двум табличным значениям приближенно определяется промежуточное значение, называется интерполированием.
Пример:
Найти lg474,7, если lg 474 = 2,6758, a lg 475 = 2,6767.
Решение:
При увеличении числа на единицу логарифм его увеличился на 0,0009, так как 2,6767—2,6758 = 0,0009. На сколько увеличится логарифм, если число увеличится на 0,7? Предполагая, что приращения логарифмов пропорциональны приращениям логарифмируемых чисел, имеем
Таким образом, логарифм должен увеличиться на 0,0006, т. е.
Действительно, по пятизначным таблицам логарифмов видно, что
Мы получили правильный результат.
Употребление четырехзначных логарифмических таблиц
К таблицам логарифмов приложены объяснения, в которых показано, как следует пользоваться таблицами для отыскания логарифмов чисел и отыскания чисел по их логарифмам. Здесь поэтому нет надобности давать еще раз эти объяснения. Ограничимся рассмотрением примера. Пусть надо вычислить
Прежде всего следует, не вдаваясь в точные вычисления, определить, какой следует ожидать ответ. Так как 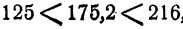
Так 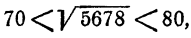
Мы видим, что ответ следует ожидать приблизительно равный 8.
Действия над логарифмами с отрицательными характеристиками
При вычислениях при помощи таблиц логарифмов часто приходится производить сложение и вычитание логарифмов, умножение логарифма на натуральное число, деление логарифма на натуральное число.
Эти действия производятся по обычным схемам с учетом незначительной особенности, вызванной тем, что характеристика логарифма может быть отрицательной.
Так как мантисса вычитаемого больше мантиссы уменьшаемого, к мантиссе уменьшаемого мысленно прибавляется единица, а от характеристики отнимается единица.
Если бы потребовалось 6,2344 разделить на 4, следовало бы к характеристике, прибавить —2, а к мантиссе + 2, т. е.
Пример:
Понятие об устройстве логарифмической линейки
Расскажем сначала, как при помощи двух линеек можно производить сложение и вычитание чисел.
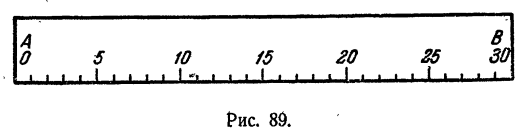
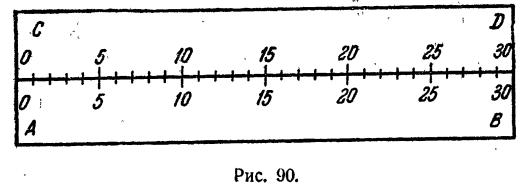
Возьмем линейку произвольной длины и разобьем ее делениями на 30 равных частей. У каждого деления поставим отметку 0, 1, 2,…, 30 (рис. 89).
Возьмем еще одну линейку такой же длины и разобьем ее на 30 равных частей так же, как и первую. Отметки на линейках должны быть расположены так, чтобы у одной из них они были нанесены на нижнем краю, а у другой —на ее верхнем краю (рис. 90).
При помощи этих двух линеек можно производить сложение и вычитание чисел.
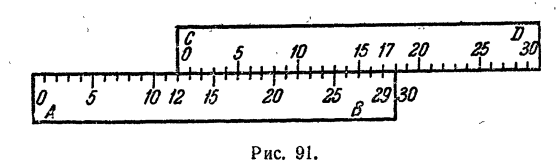
Предположим, что мы хотим к числу 12 прибавить число 17. Отметку 12 на линейке АВ поставим против отметки 0 на линейке CD. Затем найдем на линейке CD отметку 17 и прочтем противостоящую ей отметку 29 на линейке АВ. Эта отметка 29 и дает нам искомую сумму (рис. 91).
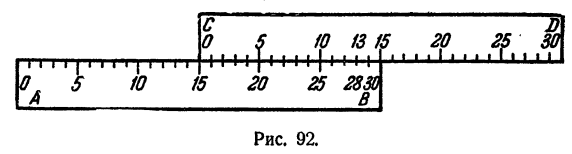
Точно так же производится вычитание. Предположим, что мы хотим от 28 отнять 13., Против отметки 28 на линейке АВ устанавливаем отметку 13 на линейке CD. Против отметки 0 на линейке CD находится отметка 15 на линейке АВ. Эта отметка 15 и дает нам искомую разность (рис. 92).
По такой же схеме ведутся вычисления и на логарифмической линейке. Различие лишь заключается в том, что при работе на логарифмической линейке складываются и вычитаются не числа, а их логарифмы.
Возьмем линейку MN произвольной длины и примем ее за единицу. У точки М поставим отметку 1, а у точки N—отметку 10. Это означает, что точка М изображает lg 1, а точка N изображает lg 10.
Отметку 2 мы ставим у точки М₂ находящейся от точки М на расстоянии приблизительно 0,3 MN. Это означает, что точка M₂ изображает lg 2 (lg 2 = 0,301).
Отметку 3 мы ставим у точки M₃, находящейся от точки М на расстоянии приблизительно 0,48 MN. Это означает, что точка М₃ изображает lg 3 (lg 3 = 0,477).
По этому же правилу ставим и остальные отметки. Получается линейка (рис. 93), на которой нанесена логарифмическая шкала.
Возьмем еще одну линейку такой же длины, как и MN, и нанесем на ней точно такую же шкалу, как и на MN. Отметки на линейках и здесь должны быть расположены так, чтобы у одной из них они были нанесены на нижнем краю, а у другой — на ее верхнем краю (рис. 94).
Из способа построения шкал на линейках МN и PQ вытекает, что сложение, произведенное при помощи линеек с логарифмическими шкалами, означает сложение логарифмов и, следовательно, может быть использовано для умножения чисел, логарифмы которых складывались.
Вычитание, произведенное при помощи линеек с логарифмическими шкалами, означает вычитание логарифмов и, следовательно, может быть использовано для деления чисел, логарифмы которых вычитались.
Из сказанного вытекают следующие правила умножения и деления чисел на логарифмической линейке.
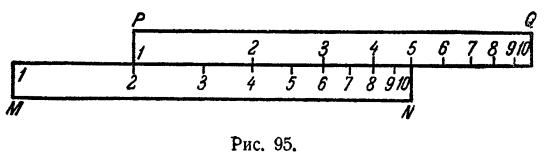
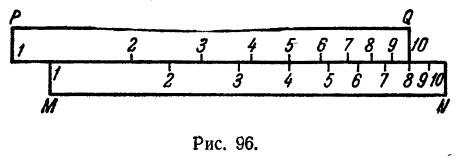
Правило умножения. Для того чтобы при помощи двух одинаковых линеек МN и PQ с логарифмическими шкалами перемножить два числа тип, нужно на линейке МN отыскать деление с отметкой m и поставить это деление против отметки 1 или 10 на линейке PQ. Затем на линейке PQ отыскать деление с отметкой n и прочесть на линейке МN противостоящую отметку, которая и даст искомое произведение.
Правило деления. Для того чтобы при помощи двух одинаковых линеек с логарифмическими шкалами разделить число m на n, нужно отметку m на линейке МN поставить против отметки n на линейке PQ. Частное будет дано отметкой ла линейке МN, находящейся против отметки 1 или 10 на линейке PQ.
На рис. 95 показано умножение 2 на 3. На рис. 96 показано умножение 8 на 5. На этих же рисунках показано и деление 6 на 3 (рис. 95) и деление 40 на 5 (рис. 96).
Устройство логарифмической линейки изложено здесь очень кратко и только для того, чтобы помочь учащемуся сделать первые шаги для ознакомления с этим простейшим счетным прибором. Для того
чтобы научиться быстро считать на логарифмической линейке, нужно упражняться и попутно ознакомиться с подробным описанием линейки, и правилами ее использования.
Для приближенных вычислений логарифмическая линейка, длина шкалы которой 25 см, может заменить таблицы трехзначных логарифмов.
Решение некоторых трансцендентных уравнений
Мы рассматривали уравнения первой степени, квадратные, биквадратные, иррациональные. Все эти уравнения относятся к классу алгебраических уравнений.
Помимо алгебраических уравнений, рассматриваются уравнения неалгебраические, или трансцендентные.
Мы рассмотрим некоторые трансцендентные уравнения: уравнения, содержащие неизвестное в показателе степени (показательные уравнения), и уравнения, содержащие неизвестное под знаком логарифма (логарифмические уравнения).
Пример:
Решить уравнение
Решение:
Предположим, что уравнение имеет решение. Тогда
Так как степени числа 2 равны, то должны быть равны и показатели степеней
Проверка показывает, что оба решения удовлетворяют уравнению.
Пример:
Решить уравнение
Решение:
Допустим, что уравнение имеет решение. Тогда
Так как степени числа 3 равны, должны быть равны и показатели степеней
Проверка показывает, что найденное решение удовлетворяет уравнению.
Пример:
Решить уравнение
Решение:
Предположим, что уравнение имеет решение. Тогда, положив 5ᵡ = у, получим
Второе значение для у должно быть отброшено, так как 5ᵡ не может равняться отрицательному числу. Остается
Проверка показывает, что это решение удовлетворяет уравнению.
Пример:
Решить уравнение 15ᵡ = 43. ‘
Решение:
Это уравнение имеет единственное решение (свойство 6 показательной функции). Логарифмируя, имеем
Пример:
Решение:
Предположим, что уравнение имеет решение, тогда
Из равенства логарифмов двух чисел следует и равенство чисел
Итак, если рассматриваемое уравнение имеет решения то этими решениями могут быть только
Первое из этих значений не удовлетворяет уравнению, так как при х=- 1 под знаком логарифма оказывается отрицательное число.
Ответ.
Пример:
Решить уравнение
Решение:
Предположим, что уравнение имеет решение. Тогда логарифмы левой и правой частей должны быть равны:
Положим lg х = у. Имеем:
Оба значения неизвестного удовлетворяют уравнению.
Ответ.
Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:




















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Степенные, показательные, логарифмические функции, их свойства и графики.
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
Технологическая карта теоретического занятия №65
ПД.01: Математика: алгебра и начала математического анализа; геометрия
2. Преподаватель Романова М. А.
3. Тема : Степенные, показательные, логарифмические функции, их свойства и графики.
4. Цели учебного занятия:
1. Познакомиться с понятием степенных, показательных и логарифмических функций, их свойствами
2. Научить работать со свойствами
1. Развить представления о роли месте математики в современном мире
2. Развить навыки конспектирования по предмету
1. Воспитать интерес к математике
2. Воспитать стремление совершенствовать профессиональные навыки современного специалиста
3. Воспитать уверенность при освоении нового материала
5. Тип занятия : УИНМ;
6. Вид занятия: лекция;
1. Учебно-наглядные и натуральные пособия, раздаточный материал
2. Технические средства обучения доска (белая доска), мел (цветные маркеры)
3. Литература основная ( учебники, конспекты лекций)
8. Учебные материалы:
1. Башмаков М . И . Математика: учебник для студ. учреждений сред. проф. образования. — М., 2014.
2. Башмаков М . И . Математика. Задачник: учеб. пособие для студ. учреждений сред. проф. образования. — М., 2014.
3. Башмаков М . И . Математика. Сборник задач профильной направленности: учеб. пособие для студ. учреждений сред. проф. образования. — М., 2014.
9. Метод проведения : 1, 2.
Хронологическая карта занятия
Вступление, мотивация изучения темы:
— формулировка темы лекции, характеристика ее профессиональной значимости, новизны и степени изученности;
— изложение плана лекции, включающего основные вопросы, подлежащие рассмотрению;
— характеристика рекомендуемой литературы.
Актуализация имеющихся знаний, ретроспекция (вопросы, изученные на прошлой лекции, связь их с новым материалом).
Основная часть лекции (изложение содержания в соответствии с планом).
Обобщение и систематизация изученного материала.
Вступление, мотивация изучения темы:
Актуализация имеющихся знаний:
Класс степенных функций является одним из самых обширных и часть применяемых. Вы в школьной программе познакомились с линейной функцией, квадратичной и кубической параболой, гиперболой, квадратным корнем. Сегодня мы повторяем всё ранее изученное и останавливается на детельном изучении свойств степенной функции.
Основная часть лекции:
Если переменные y и x прямо пропорциональны , то функциональная зависимость между ними выражается уравнением:
где k — постоянная величина ( коэффициент пропорциональности ).
График прямой пропорциональности – прямая линия, проходящая через
начало координат и образующая с осью X угол 
t g 
Поэтому, коэффициент пропорциональности называется также угловым коэффициентом . На рис.8 показаны три графика для k = 1/3, k = 1 и k = -3 .
Линейная функция. Если переменные y и x связаны уравнением 1-ой степени:
где по крайней мере одно из чисел A или B не равно нулю, то графиком этой функциональной зависимости является прямая линия . Если C = 0, то она проходит через начало координат, в противном случае — нет. Графики линейных функций для различных комбинаций A , B , C показаны на рис.9.
Обратная пропорциональность. Если переменные y и x обратно пропорциональны , то функциональная зависимость между ними выражается уравнением: y = k / x ,
где k — постоянная величина.
График обратной пропорциональности – гипербола ( рис.10 ).
У этой кривой две ветви. Как показано на рис.10, произведение координат точек гиперболы есть величина постоянная, в нашем примере равная 1. В общем случае эта величина равна k , что следует из уравнения гиперболы: xy= k .
Основные характеристики и свойства гиперболы:
1. область определения функции: x 

2. функция монотонная ( убывающая ) при x 0 и при x > 0 , но не
монотонная в целом из-за точки разрыва x = 0 ( подумайте, почему ? );
3. функция неограниченная, разрывная в точке x = 0,
4 . нулей функция не имеет.
Квадратичная функция. Это функция: y = ax 2 + bx + c , где a, b, c — постоянные, a 
График функции y = ax 2 + bx + c — тоже квадратная парабола того же вида, что и y = ax 2 , но её вершина лежит не в начале координат, а в точке с координатами:
Форма и расположение квадратной параболы в системе координат полностью зависит от двух параметров: коэффициента a при x 2 и дискриминанта D : D = b 2 – 4 ac . Эти свойства следуют из анализа корней квадратного уравнения.
Основные характеристики и свойства квадратной параболы:
— область определения функции: — 


значений: … ( ответьте, пожалуйста , на этот вопрос сами ! );
— функция в целом не монотонна, но справа или слева от вершины
ведёт себя, как монотонная;
— функция неограниченная, всюду непрерывная, чётная при b = c = 0,
— при D D 
Степенная функция. Это функция: y = ax n , где a , n – постоянные. При n = 1 получаем прямую пропорциональность : y = ax ; при n = 2 — квадратную параболу ; при n = -1 — обратную пропорциональность
или гиперболу . Таким образом, эти функции — частные случаи степенной
функции. Мы знаем, что нулевая степень любого числа, отличного от нуля, равна 1, следовательно, при n = 0 степенная функция превращается в постоянную величину: y = a , т.e. её график — прямая линия, параллельная оси Х , исключая начало координат. Все эти случаи ( при a = 1 ) показаны на рис.13 ( n 
Если n – целые, степенные функции имеют смысл и при x n чётным числом или нечётным. На рис.15 показаны две такие степенные функции: для n = 2 и n = 3.
При n = 2 функция чётная и её график симметричен относительно оси Y . При n = 3 функция нечётная и её график симметричен относительно начала координат. Функция y = x 3 называется кубической параболой .
На рис.16 представлена функция 
Показательная функция. Функция y = a x , где a — положительное постоянное число, называется показательной функцией .
Аргумент x принимает любые действительные значения ; в качестве значений функции рассматриваются только положительные числа , так как иначе мы имеем многозначную функцию. Так, функция y = 81 x имеет при x = 1/4 четыре различных значения: y = 3, y = -3, y = 3 i и y = -3 i (проверьте,пожалуйста !). Но мы рассматриваем в качестве значения функции только y = 3. Графики показательной функции для a = 2 и a = 1/2 представлены на рис.17. Они проходят через точку ( 0, 1 ). При a = 1 мы имеем график прямой линии, параллельной оси Х , т.e. функция превращается в постоянную величину, равную 1. При a > 1 показательная функция возрастает, a при 0 a
Основные характеристики и свойства показательной функции:
— область определения функции: — 


область значений: y > 0 ;
— функция монотонна: возрастает при a > 1 и убывает при 0 a
— функция неограниченная, всюду непрерывная, непериодическая;
— нулей функция не имеет.
7. Логарифмическая функция.
Пусть а — положительное число, не равное 1.
Определение . Функцию, заданную формулой
называют логарифмической функцией с основанием а .
Перечислим основные свойства логарифмической функции.
1 . Область определения логарифмической функции — множество всех положительных чисел R + , т. е. D(log a )=R + . Действительно, каждое положительное число х имеет логарифм по основанию а .
2 . Область значений логарифмической функции — множество всех действительных чисел. В самом деле, по определению логарифма любого действительного у справедливо равенство
т. е. функция y = log a x принимает значение у 0 в точке x 0 = a у0
3 . Логарифмическая функция на всей области определения возрастает (при а>1) или убывает (при 0
Докажем , например, что при а>1 функция возрастает (в случае 0
Пусть x 1 и x 2 — произвольные положительные числа и x 2 >x 1 . Надо доказать, что log a x 2 >log a x 1 . Допустим противное, т. е. что log a x 2 ≤log a x 1 (3)
Так как показательная функция у = а х при а>1 возрастает, из неравенства (3) следует : a log a x 2 ≤ a log a x 1 . (4)
Но a log a x 2 = x 2 , a log a x 1 = x 1 (по определению логарифма), т. е. неравенство (4) означает, что x 2 ≤ x 1 . Это противоречит допущению x 2 > x 1 .
Для построения графика заметим, что значение 0 логарифмическая функция принимает в точке 1; log a 1 = 0 при любом а > 0, так как а 0 = 1.
Вследствие возрастания функции при а >1 получаем, что при х > 1 логарифмическая функция принимает положительные значения, а при 0
Если 0 a x убывает на R + , поэтому log a x > 0 при 0 a x 1.
Опираясь на доказанные свойства, нетрудно построить график функции y = log a х при а>1 (рис. 1, а) и 0
Справедливо следующее утверждение:
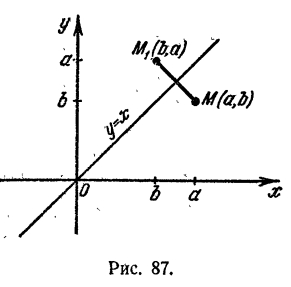
Графики показательной и логарифмической функций, имеющих одинаковое основание, симметричны относительно прямой у = х (рис. 2).
Обобщение и систематизация изученного материала:
Как записывается степенная функция в общем виде ?
Каковы особенности поведения степенной функции при целых четных и нечетных значениях показателя?
Каковы особенности поведения степенной функции при целых отрицательоных показателя?
Сегодня Вы изучили свойства и графики степенной функций; научились
строить графики функций при различных показателях и на них иллюстрировать свойства функций
2. Конспект для ученика по теме «Степенные, показательные и логарифмические функции»
Здравствуйте! Сегодня разберем тему «Степенные, показательные и логарифмические функции».
Введение
Пропорциональные величины
Если переменные y и x прямо пропорциональны, то функциональная зависимость между ними выражается уравнением:
где k — постоянная величина (коэффициент пропорциональности).
График прямой пропорциональности – прямая линия, проходящая через начало координат и образующая
с осью X угол 
tg 
Поэтому, коэффициент пропорциональности называется также угловым коэффициентом. На рис.8 показаны три графика для k = 1/3, k = 1 и k = -3.
Линейная функция
Если переменные y и x связаны уравнением 1-ой степени:
где по крайней мере одно из чисел A или B не равно нулю, то графиком этой функциональной зависимости является прямая линия. Если C = 0, то она проходит через начало координат, в противном случае — нет. Графики линейных функций для различных комбинаций A, B, C показаны на рис.9.
Обратная пропорциональность
Если переменные y и x обратно пропорциональны, то функциональная зависимость между ними выражается уравнением: y = k / x, где k — постоянная величина. График обратной пропорциональности – гипербола (рис.10).
У этой кривой две ветви. Как показано на рис.10, произведение координат точек гиперболы есть величина постоянная, в нашем примере равная 1. В общем случае эта величина равна k, что следует из уравнения гиперболы: xy= k.
Основные характеристики и свойства гиперболы:
- область определения функции:
, область значений:
;
- функция монотонная (убывающая) при x 0, но не монотонная в целом из-за точки разрыва x = 0 (подумайте, почему?);
- функция неограниченная, разрывная в точке x = 0, нечётная, непериодическая;
- нулей функция не имеет.
Квадратичная функция
где a, b, c — постоянные, 
В простейшем случае имеем:
График этой функции квадратная парабола — кривая, проходящая через начало координат (рис.11). Каждая парабола имеет ось симметрии OY, которая называется осью параболы. Точка O пересечения параболы с её осью называется вершиной параболы.
— тоже квадратная парабола того же вида, что и 
Форма и расположение квадратной параболы в системе координат полностью зависит от двух параметров: коэффициента a при x 2 и дискриминанта D.
Эти свойства следуют из анализа корней квадратного уравнения.
Основные характеристики и свойства квадратной параболы:
— область определения функции: 

(ответьте, пожалуйста, на этот вопрос сами!);
— функция в целом не монотонна, но справа или слева от вершины ведёт себя, как монотонная;
— функция неограниченная, всюду непрерывная, чётная при b = c = 0, и непериодическая;
— при D 3 называется кубической параболой.
На рис.16 представлена функция
Эта функция является обратной к квадратной параболе y = x 2 , её график получается поворотом графика квадратной параболы вокруг биссектрисы 1-го координатного угла. Это способ получения графика любой обратной функции из графика её исходной функции.
Мы видим по графику, что это двузначная функция (об этом говорит и знак 
Такие функции не изучаются в элементарной математике, поэтому в качестве функции мы рассматриваем обычно одну из её ветвей: верхнюю или нижнюю.
Показательная функция
Функция y = a x , где a — положительное постоянное число, называется показательной функцией.
Аргумент x принимает любые действительные значения;
в качестве значений функции рассматриваются только положительные числа, так как иначе мы имеем многозначную функцию.
Так, функция y = 81 x имеет при x = 1/4 четыре различных значения:
y = 3, y = -3, y = 3 i и y = -3 i (проверьте, пожалуйста!). Но мы рассматриваем в качестве значения функции только y = 3.
Графики показательной функции для a = 2 и a = 1/2 представлены на рис.17. Они проходят через точку (0, 1). При a = 1 мы имеем график прямой линии, параллельной оси Х, т.e. функция превращается в постоянную величину, равную 1. При a > 1 показательная функция возрастает, a при 0 0;
— функция монотонна: возрастает при a > 1 и убывает при 0 у0
- Логарифмическая функция на всей области определения возрастает (при а>1) или убывает (при 0 1 функция возрастает (в случае 0 x1. Надо доказать, что loga x2>loga x1. Допустим противное, т. е. что loga x2≤loga x1 (3)
Так как показательная функция у = а х при а>1 возрастает, из неравенства (3) следует: a log a x 2 ≤ a log a x 1. (4)
Но a log a x 2 = x2, a log a x 1 = x1 (по определению логарифма), т. е. неравенство (4) означает, что x2 ≤ x1. Это противоречит допущению x2 > x1.
Для построения графика заметим, что значение 0 логарифмическая функция принимает в точке 1;
loga 1 = 0 при любом а > 0, так как а0 = 1.
Вследствие возрастания функции при а > 1 получаем, что при х > 1 логарифмическая функция принимает положительные значения, а при 0 отрицательные.
http://infourok.ru/stepennie-pokazatelnie-logarifmicheskie-funkcii-ih-svoystva-i-grafiki-2517744.html
http://shkolnik.pro/publikacii/matematika/desyati_klass/1-algebra-10-klass/step-pokaz-i-log-funkcii/konspekt-dlya-uchenika-po-teme-step-pokazi-log-funkcii.html
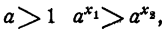 а при
а при 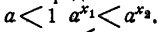 Точно так же доказывается, что нельзя предполагать, что x₁ 1 то при неограниченном возрастании показателя х функция
Точно так же доказывается, что нельзя предполагать, что x₁ 1 то при неограниченном возрастании показателя х функция 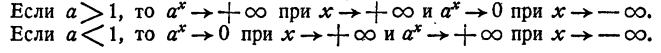
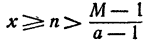
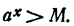
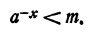
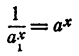
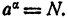
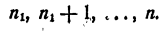


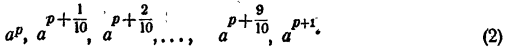
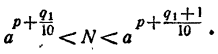
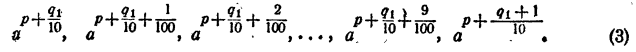
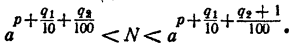
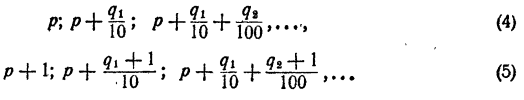
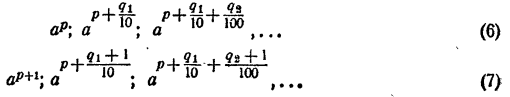
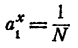
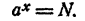
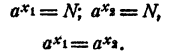
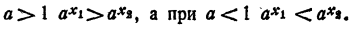

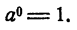
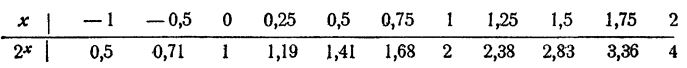
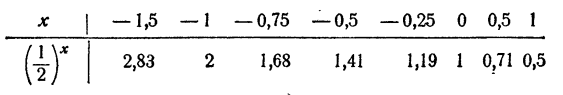
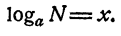
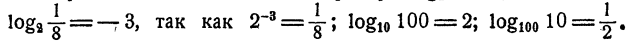
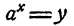
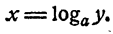
 т. е. бoльшее число имеет и бoльший логарифм. Это вытекает из свойства 3 показательной функции.
т. е. бoльшее число имеет и бoльший логарифм. Это вытекает из свойства 3 показательной функции.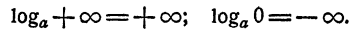
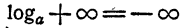 (условная запись);
(условная запись); 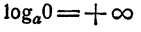 (условная запись)
(условная запись)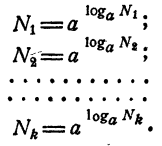
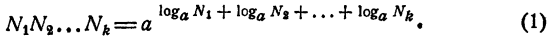
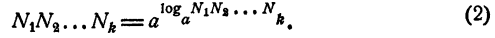
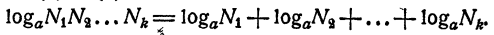
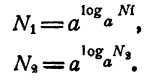
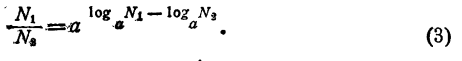

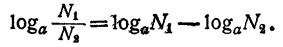
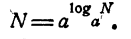


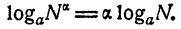
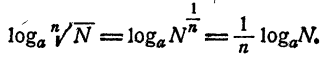
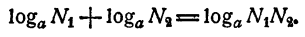
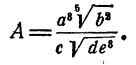
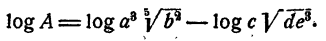
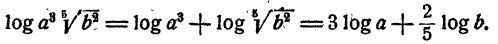
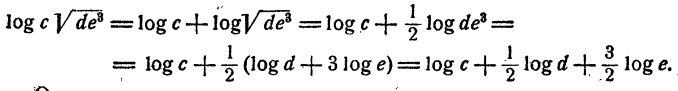
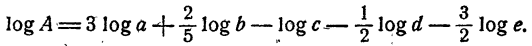
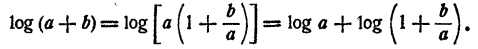
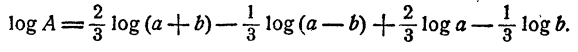
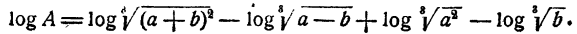
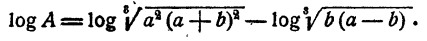
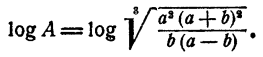
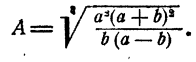
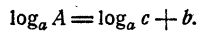
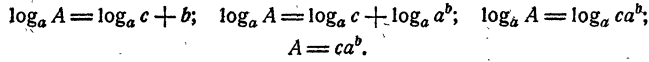
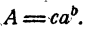
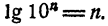
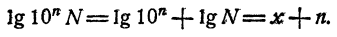

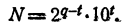

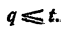
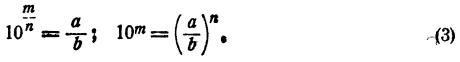
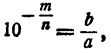

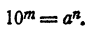

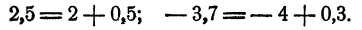
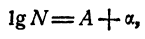
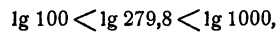
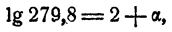
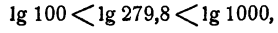
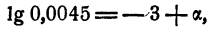
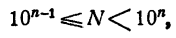
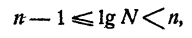
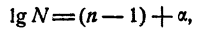
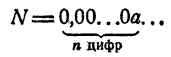
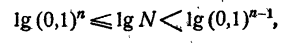

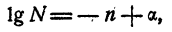
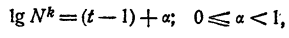
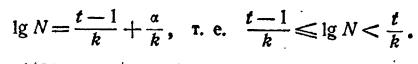
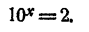
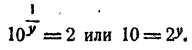
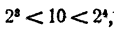
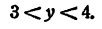
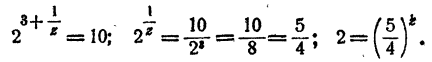
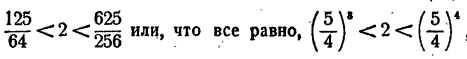
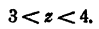
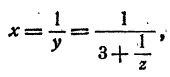
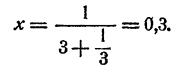
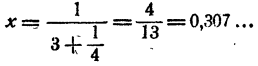
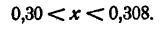
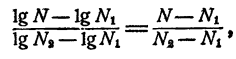
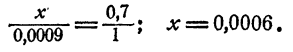
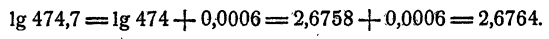
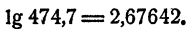
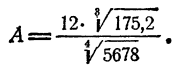
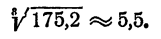
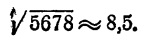
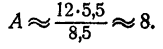
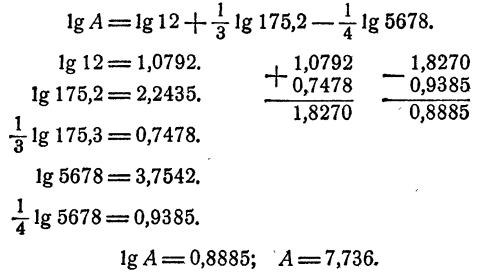
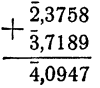
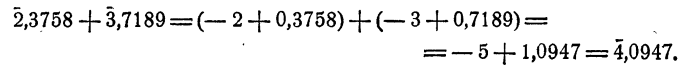

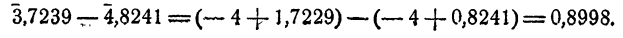
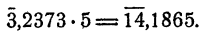
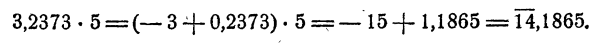
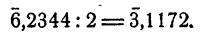
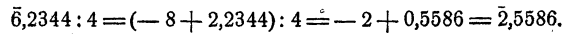
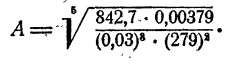

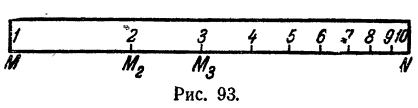
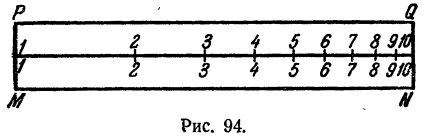
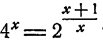
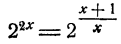
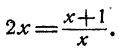
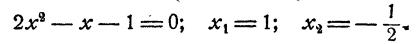
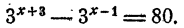
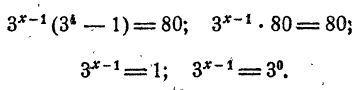
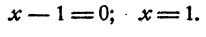
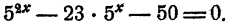
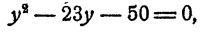
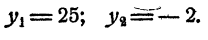
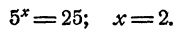
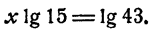
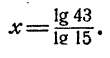
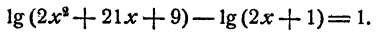

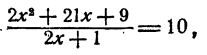
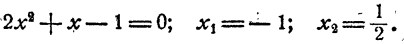
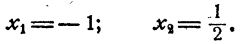
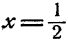
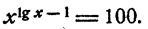
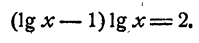
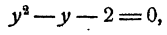
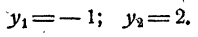
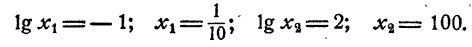
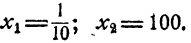


















 , область значений:
, область значений:  ;
;



