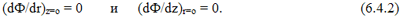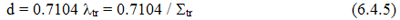Граничные условия для волнового уравнения

Волновое уравнение движущейся волны

Физика > Математическое отображение движущейся волны

Волновое уравнение – математическая формула движения волны. Рассмотрите, как вывести решение волнового уравнения, вид уравнения, граничные условия, примеры.

Наиболее общее волновое уравнение задается как u(x, t) = f (x + ct) + g (x — ct), где f и g – произвольные функции.

Задача обучения

• Вывести решение для волнового уравнения перемежающейся волны.

Основные пункты

• Любая функция u(x, t), подходящая к условию , выступает решением волнового уравнения. Для этого были введены новые переменные φ = x — ct, ψ = x + ct.
• Решения 1D-волнового уравнения – суммы левой и правой движущихся функций.
• Волновая функция также вычисляется путем получения дополнительной информации, обычно заданной граничными условиями.

Термины

• Волновое уравнение – линейной уравнение частных производных второго порядка для описания различных типов волн.
• Граничное условие – набор ограничений на границах, используемых в дифференциальных уравнениях.

Чаще всего, для одномерных волн используют уравнение:

Например, синусоидальная форма u(x, t) = A sin(kx — ωt) выступает решением волнового уравнения для с = ω/k.

Решение волнового уравнения

Отметим, что любая функция u(x, t), подходящая к условию , выступает решением волнового уравнения. Так что обратите внимание на

В середине мы использовали первое уравнение. Теперь вставим новые переменные φ = x — ct, ψ = x + ct и получим:

При смене переменных ∂u+/∂φ = 0 для уравнения со знаком «+» и ∂u-/∂ψ = 0 для знака «-». Поэтому мы видим, что

u₊(φ,ψ) = f(ψ), u_— (φ, ψ) = g(φ), где f и g – произвольные функции. Возвращаясь к исходным переменным x и t, выводим, что решение волнового уравнения:

u (х, t) = f (х + ct) + g (х — ct).

Мы видим, что решение для 1D-волнового уравнения отображает сумму левой (f) и правой (g) перемещающихся волн. Движение означает, что форма их отдельных произвольных функции по х остается стабильной, а вот время и скорость – нет.

Граничное условие

Любая функция с «x + ct» или «x — ct» может выступать решением волнового уравнения. Также можно вычислить при помощи дополнительной информации в виде граничного условия. Например, если речь идет о гитарной струне, то мы знаем, что волна обладает нулевой амплитудой на обоих концах: u (x = 0) = u (x = L) = 0.

Решение волнового уравнения в двух измерения с граничным условием нулевого смещения вдоль всего внешнего края.

Лекция 2. Вывод уравнения колебания струны

Рассмотрим струну длины l

Струной будем называть тонкую туго натянутую упругую нить.

При построени математической модели колебаний струны будем рассматривать малые колебания, происходящие в одной и той же плоскости. Пусть в состояниии покоя струна расположена вдоль оси Ox на отрезке [0,l] и при колебании каждая точка перемещается перпендикулярно оси (поперечные колебания). Тогда отклонение любой точки струны в произвольный момент времени U есть функция U(x,t) (см. рис.2).

Предположим, что натяжение столь велико, что силой тяжести и сопротивлением при изгибе можно пренебречь. Кроме того, в силу малости колебаний, будем пренебрегать также величинами высшего порядка малости по сравнению с производной U_x.

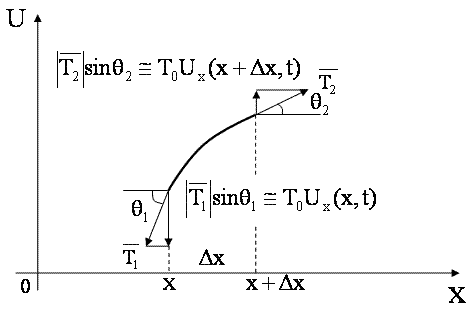
Рис. 3

Выделим малый участок струны (см. рис.3) и рассмотрим силы, действующие на него. Так как струна не сопротивляется изгибу, то ее натяжение направлено по касательной к струне в точке x. Более того, в рамках наших предположений можно считать величину силы натяжения постоянной. В самом деле, длина любого участка струны (величиной U_x 2 можно пренебречь). С ледовательно, в соответствии с законом Гука _.

Пусть ρ ( x )- линейная плотность в точке x , а γ ( x , t )- плотность внешних сил, действующих на струну в момент времени t, и направленных перпендикулярно Ox .

Результирующая сила, действующая на участок струны [ x , x +∆ x ] в направлении перпендикулярном оси OX , равна (см. рис. 3)

.

При выводе этой формулы учитываем, что при малых колебаниях

По второму закону Ньютона произведение массы на ускорение равно действующей силе mw = F , где w=U_tt, поэтому

ρ ∆ xU_tt = T ₀[ U_x ( x + ∆ x , t )- U_x ( x , t )]+ γ ( x , t ) ∆ x .

Разделим обе части равенства на Δx и устремим Δx к нулю:

ρ ( x ) U_tt = T ₀[ U_x ( x + ∆ x , t )- U_x ( x , t )]/ ∆ x + γ ( x , t ) .

Это уравнение называется уравнением вынужденных колебаний струны. Если струна однородная, то есть ρ ( x )= const , то уравнение (3) обычно записывают в виде

U_tt = a 2 U_xx + f ( x , t ),где a 2 = T ₀/ ρ ; f ( x , t )= γ ( x , t ) / ρ .

В том случае, когда на струну не действуют внешние силы, получается уравнение свободных колебаний струны

Уравнения (3) и (4) являются одномерными волновыми уравнениями (соответственно, неоднородным и однородным).

Волновыми эти уравнения называются потому, что они описывают распространение слабых возмущений в упругой среде (т.е. механические колебания с малыми амплитудами), которые в физике называют волнами. Волновые уравнения возникают также в задачах об электрических колебаниях, в гидродинамике и акустике, в теории упругости, при изучении электромагнитных полей.

Начальные условия и граничные условия.

Дифференциальные уравнения с частными производными, вообще говоря, имеют бесчисленное множество решений. Чтобы из этого множества выбрать то единственное решение, которое соответствует реальному физическому процессу (например, колебанию данной струны), надо задать некоторые дополнительные условия. В теории уравнений с частными производными, как и в обыкновенных дифференциальных уравнениях, задаются условия, называемые начальными и краевыми (граничными) условиями. Начальные условия в математической физике соответствуют состоянию физического процесса в начальный момент времени, который обычно принимают за t=0. В результате возникает задача Коши. Однако здесь есть некоторые отличия. Во-первых, начальные условия задаются для нестационарных уравнений, то есть таких уравнений, которые описывают нестационарные (зависящие от времени) процессы. Такими уравнениями являются, к примеру, волновые уравнения и уравнения теплопроводности. Во-вторых, задача Коши для уравнений с частными производными имеет единственное решение только в том случае, когда соответствующее уравнение рассматривается или на всей прямой, или на всей плоскости, или во всем пространстве. Например, это может быть задача о колебании бесконечной струны или о распространении тепла в бесконечном стержне. На практике к таким задачам приходят в том случае, когда имеется очень длинная струна или очень длинный стержень и интересуются процессами, происходящими далеко от концов, а влиянием концов пренебрегают. Если взять, допустим, длинный провод и слегка качнуть его в середине, то по нему влево и вправо побегут волны. Картина начнет искажаться только тогда, когда волны дойдут до концов провода и, отразившись, пойдут обратно. Следовательно, не учитывая влияния концов, мы тем самым не будем учитывать влияния отраженных волн.

Для волнового уравнения U_tt = a 2 U_xx задаются два начальных условия U | _{t =0} = φ ( x ), U_t | _{t =0} = ψ ( x ). Иногда их записывают иначе: U ( x , 0) = φ (х), U_t ( x , 0) = ψ (х). Первое условие физически задает начальную форму струны (начальные отклонения точек струны), а второе условие — начальные скорости точек струны. В случае волнового уравнения U_tt = a 2 Δ U на плоскости или в пространстве задаются те же два начальных условия, только функции φ и ψ , соответственно, будут зависеть от двух или трех переменных.

Если размеры струны или стержня не очень велики и влиянием концов нельзя пренебречь, то в этих случаях одни начальные условия уже не обеспечивают единственность решения задачи. Тогда необходимо задавать условия на концах. Они называются граничными условиями или краевыми условиями.Для уравнения колебаний струны часто задаются условия U | _{x =0} = 0, U | _{x = l} = 0. Иначе их записывают еще и гак: U (0, t )=0, U ( l , t ) = 0. Эти условия физически означают, что концы струны закреплены (то есть отклонения при х = 0 и при х = l в любой момент времени равны нулю). Можно задавать и другие условия на концах струны, например, U_x |_х=0= 0 , U_x |_{х= l} = 0. Такие условия возникают в следующей задаче.

Пусть концы сруны перемещаются вдоль вертикальных направляющих без трения (см. рис.4).

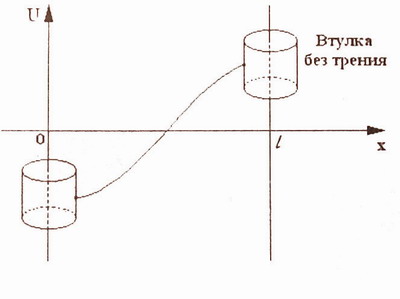
рис.4

Так как вертикальные силы, действующие на левый и правый концы струны, определяютя выражениями T ₀ U_x ( O , t ) и T ₀ U_x (l, t ) (см рис. 2), то записанные выше условия означают, что на концы струны не действуют никакие силы(поэтому такие условия называют еще условиями свободных концов).

Как было уже сказано, волновое уравнение U_tt = a 2 U_xx описывает не только колебания струны, но и другие волновые процессы, к примеру, продольные колебания пружины, продольные колебания стержня, крутильные колебания вала. В этих задачах возникают граничные условия и других видов. Подробно такие задачи мы изучать не будем. Однако приведем основные типы граничных условий. Обычно рассматривают три типа:

Граничные условия (5), (6) и (7) называются однородными, если правые части g₁(t) и g₂(t) тождественно равны нулю при всех значениях t. Если хотя бы одна из функций в правых частях не равна нулю, то граничные условия называются неоднородными.

Аналогично формулируются граничные условия и в случае трех или четырех переменных при условии, что одна из этих переменных — время. Г раницей в этих случаях будет или замкнутая кривая Г, ограничивающая некоторую плоскую область, или замкнутая поверхность Ω, ограничивающая область в пространстве. Соответственно изменится и производная от функции, фигурирующая в граничных условиях второго и третьего рода. Это будет производная по нормали n к кривой Г на плоскости или к поверхности Ω в пространстве, причем, как правило, рассматривают нормаль, внешнюю по отношению к области(см.рис. 5 ) .

К примеру, граничное условие (однородное) первого рода на плоскости записывается в виде U|_Γ=О, в пространстве U|_Ω=0. Граничное условие второго рода на плоскости имеет вид ,а в пространстве . Конечно, физический смысл этих условий разный для различных задач.

При постановке начальных и граничных условий возникает задача об отыскании решения дифференциального уравнения, удолетворяющего заданным начальным и граничным (краевым) условиям. Для волнового уравнения (3) или (4), начальных условий U(x,0)= φ(x), U_t (x,0)=ψ(x) и в случае граничных условий первого рода (5), задача называется первой начально-краевой задачей для волнового уравнения. Если вместо граничных условий первого рода задавать условия второго рода (6) или третьего рода (7), то задача будет называться, соответственно, второй и третьей начально-краевой задачей. Если граничные условия на разных участках границы имеют различные типы, то такие начально-краевые задачи называют смешанными.

6.4.1. Граничные условия для решения волнового уравнения

Предпо­ложим вначале для простоты, что речь идет о гомогенной цилиндрической активной зоне, окруженной пустотой (вакуумом). Почему именно пустотой?

Дело в том, что вакуум, кроме того, что он даёт возможность срав­нивать различные критические активные зоны в одинаковых условиях, яв­ляется в некотором смысле абсолютным поглотителем утекающих из актив­ной зоны нейтронов, поскольку он не содержит в себе объектов, с кото­рыми нейтрон может столкнуться, изменить направление движения и вер­нуться обратно в активную зону.

Единственной точкой цилиндрической гомогенной активной зоны, о ве­личине плотности потока тепловых нейтронов в которой мы можем хоть что-то ска­зать, является центр её (середина её высоты по оси симметрии). И един­ственное, что мы можем сказать относительно плотности потока тепловых нейтронов в этой точке, — то, что величина Ф(r) в ней максимальна, по­скольку это — наиболее удалённая от всех границ активной зоны точка, и возможности для утечки тепловых нейтронов из неё за пределы активной зоны минимальны.

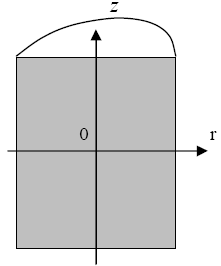
Рис.6.6. Размещение начала цилиндрической системы координат в геометрическом центре
цилиндрической активной зоны.

И если поместить начало цилиндрической системы координат в центр активной зоны (рис.6.6), то первое граничное условие:
Ф(r=0,z=0) = Ф_о = Ф_max — выглядит неопределённо, так как неясна конкретная величина это­го максимума. Это же граничное условие (как условие максимума функции Ф(r,z)) можно записать более определённо:

Второе граничное условие в такой ситуации должно быть обязательно нетривиальным, то есть должно указывать на любое конкретное значение функции Ф(r,z) в какой-либо точке активной зоны. Здесь мы выдыхаемся: при всем желании указать такую точку в пределах активной зоны мы не в состоянии, так как на границах активной зоны (при r = R_аз или z = + H_аз/2) ве­личина плотности потока тепловых нейтронов — явно не нулевая.

Поэтому в качестве второго граничного условия вводится искусствен­ное условие, состоящее в следующем.
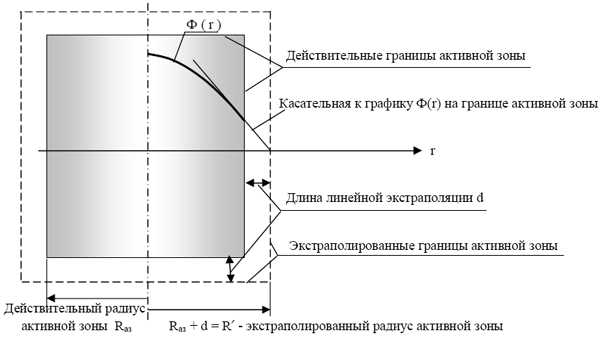
Предположим, что распределения Ф(r) и Ф(z) в пределах активной зоны от центра к периферии имеет характер нелинейного уменьшения. Но, если вообразить (рис.6.7), что функция Ф(r), переходя через границу ак­тивной зоны, продолжает уменьшаться линейно, причём, с тем же угловым коэффициентом, что и на границе активной зоны, то на некотором отстоя­нии d от границы активной зоны линейно экстраполированная таким образом функция Ф(r) уменьшается до нуля.

Отстояние (d) от границы активной зоны в вакуум, на котором ли­нейно экстраполированная на границе активной зоны функция распре­деления плотности потока тепловых нейтронов обращается в нуль, на­зывается длиной линейной экстраполяции .

Условная цилиндрическая поверхность, эквидистантно отстоящая от поверхности реальной цилиндрической активной зоны на длину ли­нейной экстраполяции, называется экстраполированной границей ак­тивной зоны .

Величины полуразмеров реальной цилиндрической активной зоны, увеличенные на длину линейной экстраполяции, называют экстраполи­рованными полуразмерами активной зоны:

Рис.6.7. К понятию длины линейной экстраполяции, экстраполирован­ных границ и экстраполированных размеров активной зоны.

Кинетическая теория даёт простую формулу для длины линейной экс­траполяции:

Учитывая сказанное, второе граничное условие звучит просто:
На экстраполированных границах активной зоны величина плотности потока тепловых нейтронов равна нулю: