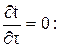Лекция 2. Вывод уравнения колебания струны
Рассмотрим струну длины l
Струной будем называть тонкую туго натянутую упругую нить.
При построени математической модели колебаний струны будем рассматривать малые колебания, происходящие в одной и той же плоскости. Пусть в состояниии покоя струна расположена вдоль оси Ox на отрезке [0,l] и при колебании каждая точка перемещается перпендикулярно оси (поперечные колебания). Тогда отклонение любой точки струны в произвольный момент времени U есть функция U(x,t) (см. рис.2).
Предположим, что натяжение столь велико, что силой тяжести и сопротивлением при изгибе можно пренебречь. Кроме того, в силу малости колебаний, будем пренебрегать также величинами высшего порядка малости по сравнению с производной Ux.
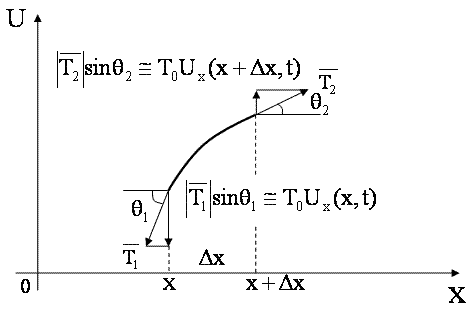
Рис. 3
Выделим малый участок струны (см. рис.3) и рассмотрим силы, действующие на него. Так как струна не сопротивляется изгибу, то ее натяжение направлено по касательной к струне в точке x. Более того, в рамках наших предположений можно считать величину силы натяжения постоянной. В самом деле, длина любого участка струны (величиной Ux 2 можно пренебречь). С ледовательно, в соответствии с законом Гука
.
Пусть ρ ( x )- линейная плотность в точке x , а γ ( x , t )- плотность внешних сил, действующих на струну в момент времени t, и направленных перпендикулярно Ox .
Результирующая сила, действующая на участок струны [ x , x +∆ x ] в направлении перпендикулярном оси OX , равна (см. рис. 3)
.
При выводе этой формулы учитываем, что при малых колебаниях
По второму закону Ньютона произведение массы на ускорение равно действующей силе mw = F , где w=Utt, поэтому
ρ ∆ xUtt = T 0[ Ux ( x + ∆ x , t )- Ux ( x , t )]+ γ ( x , t ) ∆ x .
Разделим обе части равенства на Δx и устремим Δx к нулю:
ρ ( x ) Utt = T 0[ Ux ( x + ∆ x , t )- Ux ( x , t )]/ ∆ x + γ ( x , t ) .
Это уравнение называется уравнением вынужденных колебаний струны. Если струна однородная, то есть ρ ( x )= const , то уравнение (3) обычно записывают в виде
Utt = a 2 Uxx + f ( x , t ),где a 2 = T 0/ ρ ; f ( x , t )= γ ( x , t ) / ρ .
В том случае, когда на струну не действуют внешние силы, получается уравнение свободных колебаний струны
Уравнения (3) и (4) являются одномерными волновыми уравнениями (соответственно, неоднородным и однородным).
Волновыми эти уравнения называются потому, что они описывают распространение слабых возмущений в упругой среде (т.е. механические колебания с малыми амплитудами), которые в физике называют волнами. Волновые уравнения возникают также в задачах об электрических колебаниях, в гидродинамике и акустике, в теории упругости, при изучении электромагнитных полей.
Начальные условия и граничные условия.
Дифференциальные уравнения с частными производными, вообще говоря, имеют бесчисленное множество решений. Чтобы из этого множества выбрать то единственное решение, которое соответствует реальному физическому процессу (например, колебанию данной струны), надо задать некоторые дополнительные условия. В теории уравнений с частными производными, как и в обыкновенных дифференциальных уравнениях, задаются условия, называемые начальными и краевыми (граничными) условиями. Начальные условия в математической физике соответствуют состоянию физического процесса в начальный момент времени, который обычно принимают за t=0. В результате возникает задача Коши. Однако здесь есть некоторые отличия. Во-первых, начальные условия задаются для нестационарных уравнений, то есть таких уравнений, которые описывают нестационарные (зависящие от времени) процессы. Такими уравнениями являются, к примеру, волновые уравнения и уравнения теплопроводности. Во-вторых, задача Коши для уравнений с частными производными имеет единственное решение только в том случае, когда соответствующее уравнение рассматривается или на всей прямой, или на всей плоскости, или во всем пространстве. Например, это может быть задача о колебании бесконечной струны или о распространении тепла в бесконечном стержне. На практике к таким задачам приходят в том случае, когда имеется очень длинная струна или очень длинный стержень и интересуются процессами, происходящими далеко от концов, а влиянием концов пренебрегают. Если взять, допустим, длинный провод и слегка качнуть его в середине, то по нему влево и вправо побегут волны. Картина начнет искажаться только тогда, когда волны дойдут до концов провода и, отразившись, пойдут обратно. Следовательно, не учитывая влияния концов, мы тем самым не будем учитывать влияния отраженных волн.
Для волнового уравнения Utt = a 2 Uxx задаются два начальных условия U | t =0 = φ ( x ), Ut | t =0 = ψ ( x ). Иногда их записывают иначе: U ( x , 0) = φ (х), Ut ( x , 0) = ψ (х). Первое условие физически задает начальную форму струны (начальные отклонения точек струны), а второе условие — начальные скорости точек струны. В случае волнового уравнения Utt = a 2 Δ U на плоскости или в пространстве задаются те же два начальных условия, только функции φ и ψ , соответственно, будут зависеть от двух или трех переменных.
Если размеры струны или стержня не очень велики и влиянием концов нельзя пренебречь, то в этих случаях одни начальные условия уже не обеспечивают единственность решения задачи. Тогда необходимо задавать условия на концах. Они называются граничными условиями или краевыми условиями.Для уравнения колебаний струны часто задаются условия U | x =0 = 0, U | x = l = 0. Иначе их записывают еще и гак: U (0, t )=0, U ( l , t ) = 0. Эти условия физически означают, что концы струны закреплены (то есть отклонения при х = 0 и при х = l в любой момент времени равны нулю). Можно задавать и другие условия на концах струны, например, Ux |х=0= 0 , Ux |х= l = 0. Такие условия возникают в следующей задаче.
Пусть концы сруны перемещаются вдоль вертикальных направляющих без трения (см. рис.4).
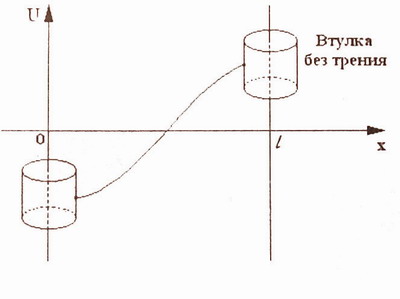
рис.4
Так как вертикальные силы, действующие на левый и правый концы струны, определяютя выражениями T 0 Ux ( O , t ) и T 0 Ux (l, t ) (см рис. 2), то записанные выше условия означают, что на концы струны не действуют никакие силы(поэтому такие условия называют еще условиями свободных концов).
Как было уже сказано, волновое уравнение Utt = a 2 Uxx описывает не только колебания струны, но и другие волновые процессы, к примеру, продольные колебания пружины, продольные колебания стержня, крутильные колебания вала. В этих задачах возникают граничные условия и других видов. Подробно такие задачи мы изучать не будем. Однако приведем основные типы граничных условий. Обычно рассматривают три типа:
Граничные условия (5), (6) и (7) называются однородными, если правые части g1(t) и g2(t) тождественно равны нулю при всех значениях t. Если хотя бы одна из функций в правых частях не равна нулю, то граничные условия называются неоднородными.
Аналогично формулируются граничные условия и в случае трех или четырех переменных при условии, что одна из этих переменных — время. Г раницей в этих случаях будет или замкнутая кривая Г, ограничивающая некоторую плоскую область, или замкнутая поверхность Ω, ограничивающая область в пространстве. Соответственно изменится и производная от функции, фигурирующая в граничных условиях второго и третьего рода. Это будет производная по нормали n к кривой Г на плоскости или к поверхности Ω в пространстве, причем, как правило, рассматривают нормаль, внешнюю по отношению к области(см.рис. 5 ) .
К примеру, граничное условие (однородное) первого рода на плоскости записывается в виде U|Γ=О, в пространстве U|Ω=0. Граничное условие второго рода на плоскости имеет вид ,а в пространстве . Конечно, физический смысл этих условий разный для различных задач.
При постановке начальных и граничных условий возникает задача об отыскании решения дифференциального уравнения, удолетворяющего заданным начальным и граничным (краевым) условиям. Для волнового уравнения (3) или (4), начальных условий U(x,0)= φ(x), Ut (x,0)=ψ(x) и в случае граничных условий первого рода (5), задача называется первой начально-краевой задачей для волнового уравнения. Если вместо граничных условий первого рода задавать условия второго рода (6) или третьего рода (7), то задача будет называться, соответственно, второй и третьей начально-краевой задачей. Если граничные условия на разных участках границы имеют различные типы, то такие начально-краевые задачи называют смешанными.
Система волновых уравнений с граничным управлением первого рода Текст научной статьи по специальности « Математика»
Похожие темы научных работ по математике , автор научной работы — Андреев Александр Анатольевич, Лексина Светлана Валентиновна
Текст научной работы на тему «Система волновых уравнений с граничным управлением первого рода»
Вестник СамГУ — Естественнонаучная серия. 2008. №2(61).
СИСТЕМА ВОЛНОВЫХ УРАВНЕНИЙ С ГРАНИЧНЫМ УПРАВЛЕНИЕМ ПЕРВОГО РОДА1
© 2008 А.А.Андреев, С.В.Лексина2
В работе получены необходимые условия на функции, определяющие начальные и финальные условия, при которых удается решить задачу управления для объектов, процесс колебания которых описывается системой волновых уравнений с граничными условиями первого рода.
1. Предварительные сведения и вводные замечания
Проблемы управления колебательными процессами имеют сравнительно небольшую историю своего развития. Впервые теоретическая постановка задачи об управлении колебаниями в достаточно четкой математической форме, как отмечено в [1], была рассмотрена А.Г. Бутковским [2] в 60 годах XX столетия. В работе Ж.-Л.Лионса [3] была исследована проблема существования граничных управлений в терминах обобщенного класса ¿2 решения волнового уравнения.
Волновое уравнение, равно как и системы волновых уравнений, служат математической моделью многих физических процессов, необходимость управлять которыми возникает, как правило, одновременно с изучением этих явлений. Возможности управления обуславливаются наличием точных аналитических решений обратных волновых задач (задач управления).
В последние годы проблеме управления были посвящены исследования В.А.Ильина, Е.И.Моисеева и их последователей 11. В.А. Ильиным в 6 доказаны необходимые и достаточные условия на функции, определяющие начальные и финальные условия, при которых удается решить задачу управления колебательным процессом в классе обобщенных решений т) волнового урав-
_ г 2 — собственные значения матрицы a, i — | о ^2 | диа-
X2 = = X2 — собственные значения матрицы A, ЛА =
тональный вид матрицы А, 5 = (1\ 12) — матрица перехода при диагонализации матрицы А.
Теорема Пусть 0 » = 0′ 0 ^ * ^ 1
ф;(Х)> — Vl(*)> = 0, 0^х^1-ХТ; 2 2X
-\(h, + ^ih, Vi (*)» = 0, XT^x^l-,
\(h, Фг1«> + ^(h, Vi W> = 0, XT^x^l-
Для нахождения управляющих функций ^(t), v(t) задачи 1.1, рассмотрим две дополнительные задачи:
задачу о гашении колебаний;
задачу о переводе первоначально покоящейся системы в заданное состояние.
Задача 1.2. Найти вектор-функции ^(t), v(t) € C2[0, T] такие, чтобы для решения u(x, t) первой краевой задачи с заданными начальными условиями [ф1, yi] в момент времени t = T выполнялись нулевые финальные условия u(x, T) = 0, ut(x, T) = 0.
Задача 1.3. Найти вектор-функции ^(t), v(t) € C2[0, T] такие, чтобы для решения u(x, t) первой краевой задачи с нулевыми начальными условиями в момент времени t = T выполнялись финальные условия с заданными функциями [ф2, ¥2].
С помощью преобразования w = S u система (1) запишется:
Witt — ^Wlxx = W2xx,
Условия (2)-(4) в данных обозначениях примут вид w(x, 0) = S ф1(х) = ф1(х) = wt(x, 0) = S ¥1(х) = \j/i(x) =
W(x, T) = S ф2(х) = ф2(х) = Wt(х, T) = S V2(x) = ф2(х) =
ф12(х) ф22(х) ф12(х) ф22(х)
w(0, t) = S [(t) = [(t) = W(l, t) = S v(t) = v(t) =
Рассмотрим решение первой краевой задачи с начальными условиями для системы (2.10):
ф11 (х + Xt) + ф11(х — Xt) 1
Xt х х l х + Xt l
, ч ф21 (х + Xt) + ф21 (х — Xt) 1
и с финальными условиями:
Ф12(х + Хг — ХТ) + Ф12(х — Хг + ХТ)
Ф’ (х + Хг — ХТ) — Ф’ (х — Хг + ХТ)
Т22(х + Хг — ХТ) + Т22(х — Хг + ХТ
Хг + х\ _ и — х + Хг
Хг + х \ х — I_, (1-х + Хг
, , Ф22(х + Хг — ХТ) + Ф22(х — Хг + ХТ) и>2(х, г) =—+
В равенствах (2.14), (2.15) функции Ф^, Шг^ — нечетные продолжения функций относительно точек х = 0, х = I, I,] — 1,2. Функции ]Г, г = 1,2 удовлетворяют условиям ¡1(7) = [1г(0 на отрезке [О, Г], [1.(0) = 0) М-.(0 = О ПРИ г Т, аналогичным условиям удовлетворяет и функция V;
Рассмотрим задачу о гашении колебаний.
Воспользуемся нулевыми финальными условиями: Wi(x, Т) = 0, Wiг(x, Т) = 0.
Выразим функции, задающие граничные управления |/(0, ^(0; г = 1,2:
ХТ) + ^^ (ф^(х — ХТ) — ^¥’21(Х — ХТ)),
—Ф’21(х + ХТ)—- Ф21(х + ХТ) + -Т21(х + ХТ)),
5^) = 2Ф21(х — ХТ) — 2^21 (X — ХТ),
V, I-:-I = -¿Ф’ (х + ХГ) — -Т21(х + ХТ).
Так как ¡д. (О = О, = О при ? ^ О, имеем: ХТ — х
^ 0, следовательно, х € [ХТ; /];
Г н—— ^ 0, следовательно, х е [0,1 — ХГ].
и>’п(х — ХТ) — ¿Тц(* — ХТ) + ¿Фи(* » ЬТ)+ х — ХТ /
Ф^(х — ХТ) — -Т21(х — ХТ) | = О, ХТ — О) + ¿Ф21ОН
+ ¿2 (ф21 (*) » ^¥21 (х)) = 0, 0 12(х — ХТ) — ^Ф22(* » ХГ)-
2у2 (ФггО) — ^У22(х)> = о,
ХТ Не можете найти то, что вам нужно? Попробуйте сервис подбора литературы.
В (2.21) сделаем замены г = — и г = —-— соответственно. Воспользуемся свой-
ствами продолжения функций Фа, Тг2, г = 1,2 относительно точек х = 0 и х = I,
учитывая, что К(г — Т) € [-КТ; I — КТ] и I — К(г — Т) € [КТ; I + КТ]:
^(г) = —Ф[2(кТ — Хг) + -У12 (ХГ — Хг) — — ф^СХГ — Хг)-
VI(г) = -ф12(/ + Хг — ХГ) + -\|/12(/ + Хг — ХГ)+
г_ — Кг + КТ 1_ (2.20)
Проинтегрируем равенства системы (2.24) по г в пределах от г до Т. Используя условия согласования финальных и граничных условий, получаем управляющие функции в условиях задачи о переводе покоящейся системы в заданное состояние:
Ф12(ХГ — Х0 МО = -2-+ 2Х
|^Ф'(ХГ — Х0 — ¿у22(ХГ — Х0
«^йГ» + X? — ХГ) — ^у22(/ + и — ХГ) \,
— ф22(ХГ — Х0 МО = -о- +
Решение общей задачи управления в условиях первой краевой задачи для системы (2.10) имеет вид:
Подставляя (2.20) и (2.25) в (2.26), получаем выражения (2.9), тогда граничные управления для исходной системы (1.1) имеют вид (2.7) и (2.8).
Представленная работа является продолжением исследований [18, 20, 21].
В заключении отметим, что система (1.1) описывает продольно-крутильное колебание длинной естественно закрученной нити [22, 23].
[1] Знаменская, Л.Н. Управление упругими колебаниями / Л.Н. Знаменская. -М.: ФИЗМАТЛТИТ, 2004. — 176 с.
[2] Бутковский, А.Г. Теория оптимального управления системами с распределенными параметрами / А.Г. Бутковский. — М.: Наука, 1965. — 474 с.
[3] Лионс, Ж.-Л. Оптимальное управление системами, описываемыми уравнениями с частными производными / Ж.-Л. Лионс. — М.: Мир, 1972. — 414 с.
[4] Ильин, В.А. Волновое уравнение с граничным управлением на двух концах за произвольный промежуток времени / В.А.Ильин // Дифференциальные уравнения. — 1999. — Т. 35. — №11. — С. 1517-1534.
[5] Ильин, В.А. Граничное управление процессом колебаний на двух концах / В.А.Ильин // Докл. РАН. — 1999. — Т. 369. — №5. — С. 592-596.
[6] Ильин, В.А. Граничное управление процессом колебаний на одном конце при закрепленном втором конце / В.А.Ильин // Докл. РАН. — 1999. — Т. 369. -№6. — С. 732-735.
[7] Ильин, В.А. Волновое уравнение с граничным управлением на одном конце при закрепленном втором конце / В.А. Ильин // Дифференциальные уравнения. — 1999. — Т. 35. — №12. — С. 1640-1659.
[8] Ильин, В.А. Граничное управление радиально-симметричными колебаниями круглой мембраны / В.А.Ильин, Е.И.Моисеев // Докл. РАН. — 2003. -Т. 393. — №6. — С. 730-734.
[9] Никитин, А.А. Граничное управление упругой силой на одном конце струны /
A.А.Никитин // Докл. РАН. — 2006. — Т. 406. — №4. — С. 458-461.
[10] Сабитова, Ю.К. О гладкости решения задачи граничного управления на двух концах для уравнения струны / Ю.К. Сабитова // Дифференциальные уравнения. — 2006. — Т. 42. — №1. — С. 133-134.
[11] Ильин, В.А. Волновое уравнение с краевым управлением / В.А.Ильин,
B.В.Тихомиров // Дифференциальные уравнения. — 1999. — Т. 35. — №1. —
[12] Знаменская, Л.Н. Управление колебаниями струны в классе обобщенных решений из ¿2 / Л.Н. Знаменская // Дифференциальные уравнения. — Т. 38. -№5. — С. 666-672.
[13] Боровских, А.В. Формулы граничного управления неоднородной струной I / А.В.Боровских // Дифференциальные уравнения. — 2007. — Т.43. — №1. -С. 64-89.
[14] Боровских, А.В. Формулы граничного управления неоднородной струной II / А.В. Боровских // Дифференциальные уравнения. — 2007. — Т. 43. — №5. -С. 640-649.
[15] Ильин, В.А. О граничном управлении на одном конце процессом, описываемым телеграфным уравнением / В.А.Ильин, Е.И.Моисеев // Докл. РАН. -2002. — Т. 387. — №5. — С. 600-603.
[16] Егоров, А.И. Управления колебаниями связанных объектов с распределенными и сосредоточенными параметрами / А.И.Егоров, Л.Н.Знаменская // Вы-числ. матем. и матем. физика. — 2005. — Т. 45. — №10. — С. 1766-1784.
[17] Егоров, А.И. Управляемость упругих колебаний систем с распределенными и сосредоточенными параметрами по двум концам / А.И. Егоров, Л.Н. Знаменская // Вычисл. матем. и матем. физика. — 2006. — Т. 46. — №11. -С. 2032-2044.
[18] Егоров, А.И. Управление упругими колебаниями (обзор) / А.И. Егоров, Л.Н. Знаменская // Оптимизация, Управление, Интеллект (Труды международной конференции CDS’2000) Институт динамики систем и теории управления СО РАН, Иркутск 2000. — Иркутск: Изд. Иркутского государственного университета, 2001. — С. 104-112.
[19] Андреев, А.А. О граничном управлении системы продольно-крутильных колебаний / А.А.Андреев, С.В.Лексина // СамДиф-2007: конференция «Дифференциальные уравнения и их приложения», г. Самара, 29 января — 2 февраля 2007 г. — Самара: Издательство «Универс групп», 2007. — С. 156.
[20] Лексина, С.В. Аналог формулы Даламбера для системы волновых уравнений / С.В. Лексина // Дифференциальные уравнения, теория функций и приложения. Международная конференция, посвященная 100-летию со дня рождения академика И.Н. Векуа (Новосибирск, 26.05-02.06.2007г.): Тез. докл. / Новосибирский гос. университет. — Новосибирск, 2007. — С. 216-216.
[21] Андреев, А.А. Смешанные задачи для системы волновых уравнений / А.А. Андреев, С.В. Лексина // Обзор прикладной и промышленной математики. — 2007. — Т. 14. — №5, С. 847-848.
[22] Горошко, О.А. К вопросу о продольно-крутильных колебаниях упругой естественно закрученной нити (каната) переменной длины с концевым грузом, движущимся по жестким направляющим: В кн.: Стальные канаты / О.А. Горошко, А.А. Чиж. — Киев: Техника, 1964. — Т. 1. — С. 56-64.
[23] Горошко, О.А. Введение в механику деформируемых одномерных тел переменной длины / О.А.Горошко, Г.Н.Савин. — Киев: Наукова думка, 1971. -225 с.
Поступила в редакцию 26/77/2008; в окончательном варианте — 26/77/2008.
A SYSTEM OF WAVE EQUATIONS WITH A BOUNDARY CONTROL OF THE FIRST KIND3
© 2008 A.A.Andreev, S.V.Lexina4
In the paper the control problem for oscillations described by the system of wave equations with boundary condition of the first kind is considered. Necessary conditions for the functions determining initial and final conditions are obtained.
Paper received 26/77/2008; Paper accepted 26/77/2008.
и граничных условиях первого рода
теплопроводность
1.1. Основной закон теплопроводности
Если в твердом теле, неподвижной жидкости или газе температура в различных точках неодинакова, то, как показывает опыт, теплота самопроизвольно переносится от участков с более высокой температурой к участкам с более низкой температурой. Такой процесс называется теплопроводностью. Перенос внутренней энергии в форме теплоты при этом осуществляется вследствие теплового движения и энергетического взаимодействия между микрочастицами (молекулами, атомами, электронами), из которых состоит данное тело.
Процесс теплопроводности неразрывно связан с распределением температуры внутри тела. Поэтому при его изучении необходимо установить понятия температурного поля и градиента температуры
а) Температурное поле. Под температурным полем понимают совокупность значений температуры во всех точках тела в данный момент времени.
В общем случае математическое описание температурного поля имеет вид:
t = f (x, y, z, t). (1.1)
Это уравнение трехмерного неустановившегося (нестационарного) температурного поля, так как температура зависит от положения точки тела (ее координат) и времени t. Если температура в любой точке тела не изменяется во времени, а является лишь функцией координат, то имеет место трехмерное установившееся (стационарное) температурное поле:

В случае одномерного стационарного температурного поля температура изменяется только вдоль одной координаты t = f (x).
б) Градиент температуры. При любом температурном поле имеются точки с одинаковой температурой. Геометрическое место таких точек образует изотермическую поверхность. Так как в одной и той же точке пространства одновременно не может быть двух различных температур, то изотермические поверхности друг с другом не пересекаются; они замыкаются на себя или оканчиваются на границах тела. Изменение температуры в теле наблюдается лишь в направлениях, пересекающих изотермические поверхности (например, направление х, рис. 1.1). При этом наибольший перепад температуры на участке единичной длины происходит в направлении нормали (n) к изотермической поверхности.
Рис. 1.1. К определению температурного градиента
Градиент температуры (gradt) – есть вектор, направленный по нормали n к изотермической поверхности в сторону возрастания температуры, модуль которого численно равен производной от температуры по этому направлению

где 

Градиент температуры характеризует неравномерность ее распределения в объеме системы и представляет собой максимальную скорость изменения температуры вдоль нормали к изотермической поверхности.
в) Тепловой поток. В теории теплообмена используются понятия теплового потока Q, Вт и поверхностной плотности теплового потока q, Вт/м 2 .
Полным тепловым потоком Q называется количество теплоты, проходящее через какую-либо изотермическую поверхность F в единицу времени.
Поверхностной плотностью теплового потока q называется количество теплоты, проходящее в единицу времени через единицу заданной изотермической поверхности тела.
Тепловой поток и поверхностная плотность теплового потока – векторы, направленные по нормали к изотермической поверхности в сторону убывания температуры (противоположно направлению температурного градиента, рис. 1.1).
г) Закон Фурье. Основной закон теплопроводности сформулирован Фурье на основании обобщения опытных данных. Согласно закону Фурье вектор плотности теплового потока, передаваемого теплопроводностью, пропорционален градиенту температуры:

Знак минус обусловлен вторым законом термодинамики, согласно которому теплота переносится в направлении снижения температуры.
Уравнение (1.3) является математическим выражением закона Фурье, который лежит в основе всех теоретических и экспериментальных исследований процессов теплопроводности.
д) Коэффициент теплопроводности. Опытным путем установлено, что коэффициент пропорциональности в уравнении (1.3) есть физический параметр вещества. Он характеризует способность вещества проводить теплоту и называется коэффициентом теплопроводности. Коэффициент теплопроводности l, Вт/(м×К) численно равен плотности теплового потока при градиенте температуры равном единице. Он зависит от природы вещества, температуры, давления. Для тепловых расчетов часто применяют средние табличные значения коэффициента теплопроводности, взятые по данным теплотехнических справочников [5,8].
1.2. Дифференциальное уравнение теплопроводности
Уравнение выводится на основе закона сохранения энергии и закона Фурье. При выводе считаем тело однородным и изотропным, физические параметры постоянными, внутренние источники теплоты в теле qV, Вт/м 3 распределенными равномерно. Закон сохранения энергии в данном случае может быть сформулирован следующим образом: количество теплоты dQ1, введенное в элементарный объем dV извне за время dt вследствие теплопроводности, и dQ2 – от внутренних источников теплоты равно изменению внутренней энергии вещества dQ, содержащейся в элементарном объеме:

Количество теплоты 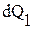


Изменение внутренней энергии вещества dQ

Подставляя значения 

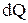

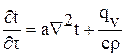
где l, с, r — коэффициент теплопроводности, Вт/(м×К), теплоемкость, Дж/(кг×К) и плотность, кг/м 3 вещества;

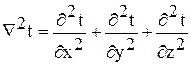
Выражение (1.5) называется дифференциальным уравнением теплопроводности. Оно устанавливает связь между временным и пространственным изменением температуры в любой точке тела, в которой происходит процесс теплопроводности.
Коэффициент пропорциональности а, м 2 /с в уравнении (1.5) является физическим параметром вещества и называется коэффициентом температуропроводности. Он важен для нестационарных тепловых процессов. Если коэффициент теплопроводности l характеризует способность тела проводить теплоту, то коэффициент температуропроводности а – быстроту выравнивания температуры тела во времени, т.е. является мерой теплоинерционных свойств тела. Выравнивание температуры во всех точках тела ( 
Если система тел не содержит внутренних источников теплоты (qV = 0), тогда выражение (1.5) принимает форму уравнения Фурье

для стационарного состояния в этом случае


Условия однозначности. Дифференциальное уравнение (1.5) выведено на основе общих законов физики и описывает явления теплопроводности в самом общем виде. Для решения конкретных задач необходимо к уравнению присоединить математическое описание частных особенностей рассматриваемого процесса (условия однозначности). Условиями однозначности называется совокупность условий, включающих геометрические условия (форма и размеры тела), его теплофизические свойства, задаваемые параметрами a, l, с, r и др., начальные условия – распределение температуры внутри тела в начальный момент времени; условия теплообмена на границах тела с внешней средой (граничные условия).
Граничные условия на внешних поверхностях тела для любого момента времени t можно задавать следующими способами:
— распределением температуры на поверхности тела 

— плотностью теплового потока для любой точки поверхности 

— температурой окружающей среды 
В качестве простейшего соотношения, связывающего плотность теплового потока qна границе тела с температурой поверхности 

где α– коэффициент теплоотдачи, характеризующий интенсивность теплообмена между поверхностью тела и окружающей средой и численно равный плотности теплового потока q при разности температур поверхности тела 

Определив плотность теплового потока q из выражения (1.3) и из соотношения (1.8), получим аналитическое выражение граничных условий III рода

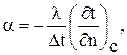
где 
Индекс «с» означает, что температурный градиент относится к поверхности тела.
Существуют еще граничные условия IV рода, когда рассматриваемое тело находится в плотном контакте с другим телом. Аналитическое выражение граничных условий IV рода описывает равенство тепловых потоков при одинаковых температурах соприкасающихся точек.
Дифференциальное уравнение теплопроводности и аналитическое выражение условий однозначности дают полную математическую формулировку конкретной задачи теплопроводности. Наиболее простые соотношения получаются при установлении стационарного режима, в котором температура тела не изменяется во времени
1.3. Теплопроводность при стационарном режиме
и граничных условиях первого рода
Рассмотрим теплопроводность тел простейшей геометрической формы, на боковых поверхностях которых поддерживается постоянная температура 

При выводе расчетных зависимостей будем считать, что стенки однородны по физическим свойствам и изотропны, тепловыделение в них отсутствует. Коэффициент теплопроводности λ принимаем постоянным λ = const, не зависящим от температуры и других факторов, режим стационарным (установившемся).
Решение задачи включает: определение закона распределения температуры по сечению стенки и вычисление теплового потока, проходящего через стенку.
Плоская стенка (рис. 1.2). Дифференциальное уравнение теплопроводности и условия однозначности для плоской стенки имеют вид:



где δ – толщина стенки.

Рис. 1.2. Распределение температуры в плоской стенке
при граничных условиях первого (I) рода
Интегрируя (1.10) получаем


где 

При х = 0 из (1.11) и (1.12) находим, что 





Из выражения (1.13) следует, что температура в стенке изменяется по линейному закону при условии λ = const.
Согласно закону теплопроводности Фурье плотность теплового потока через стенку

Плотность теплового потока прямопропорциональна коэффициенту теплопроводности, разности температур на поверхностях стенки и обратно пропорционально толщине стенки d.
Запишем соотношение (1.14) в форме закона Ома

Величину 
Общее количество теплоты Q , Дж, передаваемое через поверхность стенки площадью F за время t,

Легко доказать, что в общем случае для плоской стенки, состоящей из n слоев однородных по физическим свойствам и плотно прилегающих друг к другу, выполненных из различных материалов разной толщины плотность теплового потока q

где 


Цилиндрическая стенка(рис. 1.3). Считаем, что полый цилиндр (труба) является прямым, круглым, бесконечно длинным. Температуры на внутренней и внешней поверхностях цилиндрической стенки 




Рис. 1.3. Распределение температуры в цилиндрической стенке
при граничных условиях первого (I) рода
Введем новую переменную u, которая является градиентом температуры (gradt)
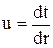
Подставляя u в уравнение (1.18) получим дифференциальное уравнение первого порядка с разделяющимися переменными

Интегрируя, получаем ur = 
Подставив 


где 

Распределение температуры по сечению цилиндрической стенки описывается уравнением логарифмической кривой.
Из граничных условий первого рода находим постоянные 


где 

Тепловой поток может быть отнесен к площади внутренней или внешней поверхности трубы, либо к ее длине.
Тепловой поток отнесенный к единице длины 
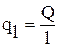


Величина 
В практических расчетах при 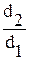


где d — средний диаметр стенки, d = 0,5 ( 

d — толщина стенки, d = 0,5 ( 

Для определения теплового потока через многослойную цилиндрическую стенку следует, как и для случая многослойной плоской стенки, просуммировать термические сопротивления отдельных слоев.

где 
Расчет температур на границах плотно соприкасающихся слоев в обеих случаях (плоская и цилиндрическая стенки) проводится по формуле:

где 


1.4. Теплопроводность плоской и цилиндрической стенок при
http://cyberleninka.ru/article/n/sistema-volnovyh-uravneniy-s-granichnym-upravleniem-pervogo-roda
http://poisk-ru.ru/s49413t1.html