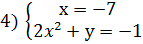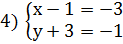Х у ху решить уравнение

math4school.ru

Уравнения в целых числах

Немного теории

Уравнения в целых числах – это алгебраические уравнения с двумя или более неизвестными переменными и целыми коэффициентами. Решениями такого уравнения являются все целочисленные (иногда натуральные или рациональные) наборы значений неизвестных переменных, удовлетворяющих этому уравнению. Такие уравнения ещё называют диофантовыми, в честь древнегреческого математика Диофанта Александрийского, который исследовал некоторые типы таких уравнений ещё до нашей эры.

Современной постановкой диофантовых задач мы обязаны французскому математику Ферма. Именно он поставил перед европейскими математиками вопрос о решении неопределённых уравнений только в целых числах. Наиболее известное уравнение в целых числах – великая теорема Ферма: уравнение

не имеет ненулевых рациональных решений для всех натуральных n > 2.

Теоретический интерес к уравнениям в целых числах достаточно велик, так как эти уравнения тесно связаны со многими проблемами теории чисел.

В 1970 году ленинградский математик Юрий Владимирович Матиясевич доказал, что общего способа, позволяющего за конечное число шагов решать в целых числах произвольные диофантовы уравнения, не существует и быть не может. Поэтому следует для разных типов уравнений выбирать собственные методы решения.

При решении уравнений в целых и натуральных числах можно условно выделить следующие методы:

способ перебора вариантов;

применение алгоритма Евклида;

представление чисел в виде непрерывных (цепных) дробей;

разложения на множители;

решение уравнений в целых числах как квадратных (или иных) относительно какой-либо переменной;

метод бесконечного спуска.

Задачи с решениями

1. Решить в целых числах уравнение x 2 – xy – 2y 2 = 7.

Запишем уравнение в виде (x – 2y)(x + y) = 7.

Так как х, у – целые числа, то находим решения исходного уравнения, как решения следующих четырёх систем:

1) x – 2y = 7, x + y = 1;

2) x – 2y = 1, x + y = 7;

3) x – 2y = –7, x + y = –1;

4) x – 2y = –1, x + y = –7.

Решив эти системы, получаем решения уравнения: (3; –2), (5; 2), (–3; 2) и (–5; –2).

Ответ: (3; –2), (5; 2), (–3; 2), (–5; –2).

2. Решить в целых числах уравнение:

а) 20х + 12у = 2013;

в) 201х – 1999у = 12.

а) Поскольку при любых целых значениях х и у левая часть уравнения делится на два, а правая является нечётным числом, то уравнение не имеет решений в целых числах.

Ответ: решений нет.

б) Подберём сначала некоторое конкретное решение. В данном случае, это просто, например,

Поскольку числа 5 и 7 взаимно простые, то

Значит, общее решение:

х = 1 + 7k, у = 2 – 5k,

где k – произвольное целое число.

Ответ: (1+7k; 2–5k), где k – целое число.

в) Найти некоторое конкретное решение подбором в данном случае достаточно сложно. Воспользуемся алгоритмом Евклида для чисел 1999 и 201:

НОД(1999, 201) = НОД(201, 190) = НОД(190, 11) = НОД(11, 3) = НОД(3 , 2) = НОД(2, 1) = 1.

Запишем этот процесс в обратном порядке:

1 = 2 – 1 = 2 – (3 – 2) = 2·2 – 3 = 2· (11 – 3·3) – 3 = 2·11 – 7·3 = 2·11 – 7(190 – 11·17) =

= 121·11 – 7·190 = 121(201 – 190) – 7·190 = 121·201 – 128·190 =

= 121·201 – 128(1999 – 9·201) = 1273·201 – 128·1999.

Значит, пара (1273, 128) является решением уравнения 201х – 1999у = 1. Тогда пара чисел

x₀ = 1273·12 = 15276, y₀ = 128·12 = 1536

является решением уравнения 201х – 1999у = 12.

Общее решение этого уравнения запишется в виде

х = 15276 + 1999k, у = 1536 + 201k, где k – целое число,

или, после переобозначения (используем, что 15276 = 1283 + 7·1999, 1536 = 129 + 7·201),

х = 1283 + 1999n, у = 129 + 201n, где n – целое число.

Ответ: (1283+1999n, 129+201n), где n – целое число.

3. Решить в целых числах уравнение:

а) x 3 + y 3 = 3333333;

б) x 3 + y 3 = 4(x 2 y + xy 2 + 1).

а) Так как x 3 и y 3 при делении на 9 могут давать только остатки 0, 1 и 8 (смотрите таблицу в разделе «Делимость целых чисел и остатки»), то x 3 + y 3 может давать только остатки 0, 1, 2, 7 и 8. Но число 3333333 при делении на 9 даёт остаток 3. Поэтому исходное уравнение не имеет решений в целых числах.

Ответ: целочисленных решений нет.

б) Перепишем исходное уравнение в виде (x + y) 3 = 7(x 2 y + xy 2 ) + 4. Так как кубы целых чисел при делении на 7 дают остатки 0, 1 и 6, но не 4, то уравнение не имеет решений в целых числах.

Ответ: целочисленных решений нет.

а) в простых числах уравнение х 2 – 7х – 144 = у 2 – 25у;

б) в целых числах уравнение x + y = x 2 – xy + y 2 .

а) Решим данное уравнение как квадратное относительно переменной у. Получим

у = х + 9 или у = 16 – х.

Поскольку при нечётном х число х + 9 является чётным, то единственной парой простых чисел, которая удовлетворяет первому равенству, является (2; 11).

Так как х, у – простые, то из равенства у = 16 – х имеем

С помощью перебора вариантов находим остальные решения: (3; 13), (5; 11), (11; 5), (13; 3).

Ответ: (2; 11), (3; 13), (5; 11), (11; 5), (13; 3).

б) Рассмотрим данное уравнение как квадратное уравнение относительно x:

x 2 – (y + 1)x + y 2 – y = 0.

Дискриминант этого уравнения равен –3y 2 + 6y + 1. Он положителен лишь для следующих значений у: 0, 1, 2. Для каждого из этих значений из исходного уравнения получаем квадратное уравнение относительно х, которое легко решается.

Ответ: (0; 0), (0; 1), (1; 0), (1; 2), (2; 1), (2; 2).

5. Существует ли бесконечное число троек целых чисел x, y, z таких, что x 2 + y 2 + z 2 = x 3 + y 3 + z 3 ?

Попробуем подбирать такие тройки, где у = –z. Тогда y 3 и z 3 будут всегда взаимно уничтожаться, и наше уравнение будет иметь вид

Чтобы пара целых чисел (x; y) удовлетворяла этому условию, достаточно, чтобы число x–1 было удвоенным квадратом целого числа. Таких чисел бесконечно много, а именно, это все числа вида 2n 2 +1. Подставляя в x 2 (x–1) = 2y 2 такое число, после несложных преобразований получаем:

y = xn = n(2n 2 +1) = 2n 3 +n.

Все тройки, полученные таким образом, имеют вид (2n 2 +1; 2n 3 +n; –2n 3 – n).

6. Найдите такие целые числа x, y, z, u, что x 2 + y 2 + z 2 + u 2 = 2xyzu.

Число x 2 + y 2 + z 2 + u 2 чётно, поэтому среди чисел x, y, z, u чётное число нечётных чисел.

Если все четыре числа x, y, z, u нечётны, то x 2 + y 2 + z 2 + u 2 делится на 4, но при этом 2xyzu не делится на 4 – несоответствие.

Если ровно два из чисел x, y, z, u нечётны, то x 2 + y 2 + z 2 + u 2 не делится на 4, а 2xyzu делится на 4 – опять несоответствие.

Поэтому все числа x, y, z, u чётны. Тогда можно записать, что

и исходное уравнение примет вид

Теперь заметим, что (2k + 1) 2 = 4k(k + 1) + 1 при делении на 8 даёт остаток 1. Поэтому если все числа x₁, y₁, z₁, u₁ нечётны, то x₁ 2 + y₁ 2 + z₁ 2 + u₁ 2 не делится на 8. А если ровно два из этих чисел нечётно, то x₁ 2 + y₁ 2 + z₁ 2 + u₁ 2 не делится даже на 4. Значит,

и мы получаем уравнение

Снова повторив те же самые рассуждения, получим, что x, y, z, u делятся на 2 n при всех натуральных n, что возможно лишь при x = y = z = u = 0.

7. Докажите, что уравнение

(х – у) 3 + (y – z) 3 + (z – x) 3 = 30

не имеет решений в целых числах.

Воспользуемся следующим тождеством:

(х – у) 3 + (y – z) 3 + (z – x) 3 = 3(х – у)(y – z)(z – x).

Тогда исходное уравнение можно записать в виде

(х – у)(y – z)(z – x) = 10.

Обозначим a = x – y, b = y – z, c = z – x и запишем полученное равенство в виде

Кроме того очевидно, a + b + c = 0. Легко убедиться, что с точностью до перестановки из равенства abc = 10 следует, что числа |a|, |b|, |c| равны либо 1, 2, 5, либо 1, 1, 10. Но во всех этих случаях при любом выборе знаков a, b, c сумма a + b + c отлична от нуля. Таким образом, исходное уравнение не имеет решений в целых числах.

8. Решить в целых числах уравнение 1! + 2! + . . . + х! = у 2 .

если х = 1, то у 2 = 1,

если х = 3, то у 2 = 9.

Этим случаям соответствуют следующие пары чисел:

Заметим, что при х = 2 имеем 1! + 2! = 3, при х = 4 имеем 1! + 2! + 3! + 4! = 33 и ни 3, ни 33 не являются квадратами целых чисел. Если же х > 5, то, так как

5! + 6! + . . . + х! = 10n,

можем записать, что

1! + 2! + 3! + 4! + 5! + . . . + х! = 33 + 10n.

Так как 33 + 10n – число, оканчивающееся цифрой 3, то оно не является квадратом целого числа.

Ответ: (1; 1), (1; –1), (3; 3), (3; –3).

9. Решите следующую систему уравнений в натуральных числах:

a 3 – b 3 – c 3 = 3abc, a 2 = 2(b + c).

3abc > 0, то a 3 > b 3 + c 3 ;

таким образом имеем

b 2 2 + х = у 4 + у 3 + у 2 + у.

Разложив на множители обе части данного уравнения, получим:

х(х + 1) = у(у + 1)(у 2 + 1),

х(х + 1) = (у 2 + у)(у 2 + 1)

Такое равенство возможно, если левая и правая части равны нулю, или представляют собой произведение двух последовательных целых чисел. Поэтому, приравнивая к нулю те или иные множители, получим 4 пары искомых значений переменных:

Произведение (у 2 + у)(у 2 + 1) можно рассматривать как произведение двух последовательных целых чисел, отличных от нуля, только при у = 2. Поэтому х(х + 1) = 30, откуда х₅ = 5, х₆ = –6. Значит, существуют ещё две пары целых чисел, удовлетворяющих исходному уравнению:

Ответ: (0; 0), (0; –1), (–1; 0), (–1; –1), (5; 2), (–6; 2.)

Задачи без решений

1. Решить в целых числах уравнение:

б) х 2 + у 2 = х + у + 2.

2. Решить в целых числах уравнение:

а) х 3 + 21у 2 + 5 = 0;

б) 15х 2 – 7у 2 = 9.

3. Решить в натуральных числах уравнение:

4. Доказать, что уравнение х 3 + 3у 3 + 9z 3 = 9xyz в рациональных числах имеет единственное решение

5. Доказать, что уравнение х 2 + 5 = у 3 в целых числах не имеет решений.

Решение уравнений в целых числах

Подготовка к профильной части ЕГЭ по математике

Просмотр содержимого документа
«Решение уравнений в целых числах»

Решение уравнений в целых числах.

Г.Дзержинск Нижегородской области.

Линейное уравнение ax+by=c

— Если НОД(a,b)=1, то уравнение имеет хотя бы одно решение:

где (x 0 ,y 0 ) — некоторое частное целочисленное

решение для t ∊Z

— Если НОД(a,b) ≠ 1, то уравнение не имеет целочисленных решений.

Пример1 : Решить в целых числах уравнение:

НОД(7 ; 9)=1, целочисленное решение (2;2), значит

Ответ: x=2+9t, y=2-7t, t ∊Z .

Пример2 : Решить в целых числах уравнение:

НОД(3 ; 4)=1, целочисленное решение (3;2), значит

Ответ: x=3-4t, y=2-3t, t ∊Z .

Замечание 1. Если ( x 0, y 0 )- целочисленное решение уравнения ax+by=1, то (cx 0 ,cy 0 ) — целочисленное решение уравнения ax+by=c.

Пример3 : Решить в целых числах уравнение:

Найдём целочисленное решение уравнения

НОД(3 ; 5)=1, целочисленное решение (2;1), значит частным

решением уравнения 3x-5y=11 является пара (22;11), т.е.

x=22-5t, y=11-3t, t ∊Z

Ответ: x=22-5t, y=11-3t, t ∊Z

Замечание 2. Если трудно подобрать частное решение, то можно применить алгоритм Евклида.

Пример 4 : Решить в целых числах уравнение:

НОД(23 ; 79)=1, значит существует целочисленное решение.

1=10-3 ⋅ 3=10-3 ⋅( 23-10 ⋅ 2)=-3 ⋅ 23+10 ⋅ 7=-3 ⋅ 23+7 ⋅( 79-23 ⋅ 3)=

-23 ⋅ 24 + 79 ⋅ 7=1, значит частным решением данного уравнения является пара чисел (24;7), т.е. решение

x=24+79t, y=7+23t, t ∊Z .

Ответ: x=24+79t, y=7+23t ,t ∊Z .

Метод разложения на множители. Пример 5 : Решить в целых числах уравнение: x+xy-3y=5 x-3+y(x-3)=5-3 (x-3)(y+1)=2 = = = Ответ:(1;-2),(2;-3),(4;1),(5;0). » width=»640″

Метод разложения на множители.

Пример 5 : Решить в целых числах уравнение:

0 = Ответ: (5;6),(-6;-5),(-3;4),(-4;3). » width=»640″

Пример 6 : Решить в целых числах уравнение:

= 91 ,91=7 ⋅ 13=1 ⋅ 91

Пример 7 : Решить в целых числах уравнение:

Рассмотрим остатки от деления на 4 чисел вида .

1) Если х и у чётные, то делится на 4.

2) Если одно из чисел чётное, а второе — нечётное, то остаток от деления на 4 выражения равен 1, т.к.

3) Если оба числа нечётные, то остаток от деления

Рассмотрим правую часть данного уравнения

4z-1=4z-4+3=4(z-1)+3 , т.е. при делении на 4 правая часть

имеет остаток 3.

Т. к. левая часть и правая часть имеют разные остатки , то

Ни при каких х , у , z уравнение решений не имеет.

Ответ: решений нет.

— Этот метод часто используется для доказательства того, что уравнение не имеет решений в целых числах.

Пример 8 : Решить в целых числах уравнение:

Метод решения относительно одной переменной

Методы решения нелинейных уравнений и неравенств в целых числах

При решении нелинейных уравнений в целых и натуральных числах можно условно выделить следующие методы:

1. Метод разложения на множители;

2. Метод решения относительно одной переменной;

4. Метод остатков;

6. Метод доказательства от противного;

7. Метод параметризации уравнения;

8. Функционально-графический метод.

Метод разложения на множители

· Вынесение общих множителей за скобку.

Задание 1. Решить в целых числах уравнение 2х 3 +ху-7=0

Решение: Приведем уравнение к виду: х(2х 2 +у)=7. Так как , то рассмотрим четыре системы уравнений:

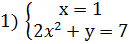
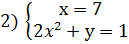
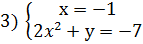
Из каждой системы получаем решения.

· Применение формул сокращенного умножения.

Задание 2. Найти все пары натуральных чисел, разность квадратов которых равна 55.

Решение: Запишем условие задачи в виде уравнения n 2 -k 2 =55 или (n-k)(n+k)=55. Так как (n+k)>0, то (n-k)>0, причем (n+k)>(n-k). Поскольку , то возможны только два случая:

. Из каждой системы получаем решения

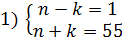
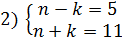
Задание 3. Решить в целых числах уравнение ху+3х-у=6..

Задание 3. Решить в целых числах уравнение ху+3х-у=6.

Решение: Запишем уравнение в виде х(у+3)-(у+3)=3 или (х-1)(у+3)=3. Так как , то рассмотрим четыре системы

Из каждой системы получаем решения.

Разложение квадратного трехчлена.

Задание 4. Решить в целых числах уравнение х 2 -3ху+2у 2 =11.

Решение: решим квадратное уравнение х 2 -3ху+2у 2 =11 относительно переменной х: х₁=у и х₂=2у. Тогда получаем: (х-у)(х-2у)=11. Так как … (продолжи решение)

Задание 5. Решить в целых числах уравнение 2х 2 -2ху++9х+у=2.

Решение: Перепишем уравнение в виде 2х 2 -х(2у-9)+у-2+а=аи разложим левую часть уравнения на множители как квадратный трехчлен относительно х. Найдем дискриминант D=4у 2 -44у+97-8а. Очевидно, если 97-8а=121, то дискриминант будет полным квадратом. При этом а=-3 и х= 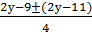. Отсюда х₁=0,5 и х₂=у-5. Уравнение принимает вид (2х-1)(х-у+5)=-3. (продолжи решение)

Метод решения относительно одной переменной

· Выделение целой части.

Задание 6 (МГУ, 1997). Найти все пары целых чисел х и у, удовлетворяющих уравнению 3ху+14х+17у+71=0

Решение: выразим из данного уравнения у через х: 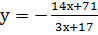. При этом следует отметить, что величина 3х+17 не равна нулю, так как х – целое число. Выделим из дроби в правой части этого равенства правильную Алгебраическую дробь (у которой степень числителя меньше степени знаменателя): . Умножим обе части последнего равенства на 3: или . Поскольку числа 3у и 14 – целые, то 3х+17 должно быть делителем числа 25, т.е. 3у+17= – всего 6 возможностей. Отсюда для х получаем три возможных значения: -4, -6, -14 (в остальных трех случаях х не является целым) Соответствующие значения у равны: -3, -13, -5.

Замечание: в данном примере суть выделения целой части состоит в избавлении переменной х из числителя. В решении был использован прием домножения обеих частей равенства на коэффициент при х в знаменателе. Этот прием домножения также удобно использовать при решении уравнений методом разложения на множители.

· Использование дискриминанта (неотрицательность).

Задание 7: Решить в целых числах уравнение 3(х 2 +ху+у 2 )=х+8у

Решение: Рассмотрим уравнение, как квадратное относительно х: 3(х 2 +ху+у 2 )-х-8у=0. Найдем дискриминант D=-27у 2 +90у+1. Данное уравнение имеет корни, если , т.е. -27у 2 +90у+1 . Т.к. то получаем, что . Перебирая эти значения, получаем решения уравнения.

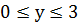
· Использование дискриминанта (полный квадрат).

Задание 7: Решить в целых числах уравнение х 2 -ху+у 2 =х+у

Решение: Рассмотрим уравнение как квадратное относительно х: х 2 –(у+1)х+у 2 -у=0. Его дискриминант D=-3у 2 +6у+1=t 2 должен быть квадратом некоторого целого числа t. Получаем новое уравнение: 3у 2 -6у-1+ t 2 =0; 3(у-1) 2 + t 2 =4. Из последнего уравнения следует, что t 2 4, .

1. Если t 2 =0, то уравнение 3(у-1) 2 =4 не имеет целого решения у.

2. Если t 2 =1, то уравнение 3(у-1) 2 =3 имеет целые решения у₁=2 и у₂=0. При у=2 получаем квадратное уравнение х 2 -3х+2=0 с корнями х=1 или х=2. При у=0 получаем квадратное уравнение х 2 -х=0 с корнями х=0 или х=1.

3. Если t 2 =4, то уравнение 3(у-1) 2 =0 имеет одно целое решение у=1. При у=1 получаем квадратное уравнение х 2 -2х=0 с корнями х=0 или х=2.

Метод оценки

· Использование известных неравенств.

Задание 8: Решить в натуральных числах уравнение

Решение: Пусть для определенности . Проведем перебор для первых значений неизвестной х.

1. Если х=1, то получаем неверное равенство 1+ , так как 1+ при любых натуральных у.

2. Если х=2, то получаем неверное равенство + , так как + при любых натуральных у.

3. Если х=3, то получаем + ; , у=6.

4. Если х=4, то получаем + ; , у=4.

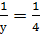
5. Если х=5, то получаем + ; , у= — не натуральное

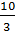
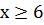
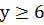
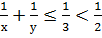
6. Пусть . По условию , следовательно, . Тогда , а значит, . Таким образом, при исходное уравнение решений не имеет.

Заметим, что в уравнении неизвестные х и у равноправны, поэтому снимая условие имеем еще одно решение (6;3). Кроме того, можно сделать вывод, что при исходное уравнение не имеет решений.

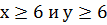
Задание 9: Решить в целых числах уравнение

Решение: Можно найти вначале решения только в натуральных числах, так как если (х₀; у₀; z₀) – решение, то, изменив знак у любых двух чисел этой тройки, снова получим решение. Данное уравнение умножим на 2xyz и воспользуемся неравенством ,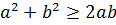

6xyz=2x 2 y 2 +2x 2 z 2 +2y 2 z 2 =(x 2 y 2 +x 2 z 2 )+(x 2 y 2 +y 2 z 2 )+(x 2 y 2 +y 2 z 2 ) 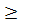2x 2 yz+2y 2 xz+2z 2 xy=2xyz(x+y+z), откуда x+y+z 3. Но х,у, z – натуральные, поэтому х=у= z=1 единственное решение в натуральных числах. Остальные решения в натуральных числах. Остальные решения исходного уравнения таковы: (-1; -1; 1); (1; -1; -1); (-1; 1; -1).

Ответ: (1; 1; 1); (-1; -1; 1); (1; -1; -1); (-1; 1; -1)

· Приведение к сумме неотрицательных выражений

Задание 10: Решить в целых числах уравнение х+у=х 2 -ху+у 2

Решение: приведем уравнение к виду (х-1) 2 +(у-1) 2 +(х-у) 2 =2. Так как (х-1) 2 2, то имеем (х-1) 2 =0 или (х-1) 2 =1. Отсюда получаем три значения х: 1, 0, 2. Подставляя эти значения в исходное уравнение, найдем значения у.