Теоремы, связанные с кривыми второго порядка
Содержание
1.Кривые второго порядка
2.Теоремы, связанные с кривыми второго порядка
Введение
Впервые кривые второго порядка изучались одним из учеников Платона. Его работа заключалась в следующем: если взять две пересекающиеся прямые и вращать их вокруг биссектрисы угла, ими образованного, то получится конусная поверхность. Если же пересечь эту поверхность плоскостью, то в сечении получаются различные геометрические фигуры, а именно эллипс, окружность, парабола, гипербола и несколько вырожденных фигур.
Однако эти научные знания нашли применение лишь в XVII, когда стало известно, что планеты движутся по эллиптическим траекториям, а пушечный снаряд летит по параболической. Ещё позже стало известно, что если придать телу первую космическую скорость, то оно будет двигаться по окружности вокруг Земли, при увеличении этой скорости — по эллипсу, а по достижении второй космической скорости тело по параболе покинет поле притяжения Земли.
Кривые второго порядка
Кривой 2-го порядка называется линия на плоскости, которая в некоторой декартовой системе координат определяется уравнением
ax2 + 2bxy + cy2 + 2dx + 2ey + f = 0
где a, b, c, d, e, f — вещественные коэффициенты, причем a2 + b2 + c2 ≠ 0 .
Вид кривой зависит от четырёх инвариантов:
инварианты относительно поворота и сдвига системы координат:
инвариант относительно поворота системы координат (полуинвариант):
Многие важные свойства кривых второго порядка могут быть изучены при помощи характеристической квадратичной формы, соответствующей уравнению кривой:
Так, например, невырожденная кривая 

Корни этого уравнения являются собственными значениями вещественной симметричной матрицы и, как следствие этого, всегда вещественны:
Кривые второго порядка классифицируются на невырожденные кривые и вырожденные.
Доказано, что кривая 2–го порядка, определяемая этим уравнением принадлежит к одному из следующих типов: эллипс, гипербола, парабола, пара прямых (пересекающихся, параллельных или совпадающих), точка, пустое множество.
Иными словами, для каждой кривой 2-го порядка (для каждого уравнения) существует такая система координат, в которой уравнение кривой имеет вид:
Эллипс
Эллипсом называется геометрическое место точек плоскости, для которых сумма расстояний до двух фиксированных точек плоскости, называемых фокусами эллипса, есть величина постоянная. Отрезки, соединяющие точку эллипса с фокусами, называются фокальными радиусами точки.
Если эллипс описывается каноническим уравнением
где a > 0 , b > 0, a > b > 0 — большая и малая полуоси эллипса, то фокусы эллипса расположены симметрично на оси абсцисс и имеют координаты (−c, 0) и ( c, 0), где
Величина e = c/a называется эксцентриситетом эллипса.
По определению эллипса r1 + r2 = 2a, r1 и r2 − фокальные радиусы, их длины вычисляются по формулам
Если фокусы эллипса совпадают, то эллипс является окружностью.
Гипербола
Гиперболой называется кривая второго порядка, которая в некоторой декартовой системе координат описывается уравнением
где a > 0, b > 0 — параметры гиперболы.
Это уравнение называется каноническим уравнением гиперболы, а система координат, в которой гипербола описывается каноническим уравнением, называется канонической.
В канонической системе оси координат являются осями симметрии гиперболы, а начало координат — ее центром симметрии.
Точки пересечения гиперболы с осью OX ( ± a, 0) называются вершинами гиперболы.
С осью OY гипербола не пересекается.
Отрезки a и b называются полуосями гиперболы.
Прямые ay − bx = 0 и ay + bx = 0 — асимптоты гиперболы, при удалении точки гиперблы в бесконечность, соответствующая ветвь гиперболы приближается к одной из асимптот.
Уравнение описывает гиперболу, вершины которой лежат на оси OY в точках (0, ± b).
Такая гипербола называется сопряженной к гиперболе её асимптоты — те прямые ay − bx = 0 и ay + bx = 0. Говорят о паре сопряжённых гипербол.
Парабола
Параболой называется кривая второго порядка, которая в некоторой декартовой системе координат описывается уравнением
где p > 0 — параметр параболы.
Такое уравнение называется каноническим уравнением параболы, а система координат, в которой парабола описывается каноническим уравнением, называется канонической.
В канонической системе ось абсцисс является осью симметрии параболы, а начало координат — её вершиной.
Уравнения y2 = −2 px, x2 = 2 py, и x2 = −2 py, p > 0, в той же самой канонической системе координат также описывают параболы:
Теоремы, связанные с кривыми второго порядка
Теоремма Паскамля — теорема проективной геометрии, которая гласит, что:
Если шестиугольник вписан в окружность либо любое другое коническое сечение (эллипс, параболу, гиперболу, даже пару прямых), то точки пересечения трёх пар противоположных сторон лежат на одной прямой. Теорема Паскаля двойственна к теореме Брианшона.
Теорема Брианшона является классической теоремой проективной геометрии. Она сформулируется следующим образом:
Если шестиугольник описан около конического сечения, то три диагонали, соединяющие противоположные вершины этого шестиугольника, проходят через одну точку.
В частности, в вырожденном случае:
Если стороны шестиугольника проходят поочерёдно через две данные точки, то три диагонали, соединяющие его противоположные вершины, проходят через одну точку.
Теорема Брианшона двойственна к теореме Паскаля, а её вырожденный случай двойственен к теореме Паппа.
Литература
1. Корн Г., Корн Т. Кривые второго порядка (конические сечения) // Справочник по математике. — 4-е издание. — М: Наука, 1978. — С. 64-69.
2. Корн Г., Корн Т. 2.4-5. Характеристическая квадратичная форма и характеристическое уравнение // Справочник по математике. — 4-е издание. — М: Наука, 1978. — С. 64.
3. В.А. Ильин, Э.Г. Позняк. Аналитическая геометрия, гл. 6. М.: «Наука», 1988.
Характеристические кривые и характеристические уравнения
Характеристическое уравнение составляется для цепи после коммутации. Оно может быть получено следующими способами:
- непосредственно на основе дифференциального уравнения вида (2) (см. лекцию №24), т.е. путем исключения из системы уравнений, описывающих электромагнитное состояние цепи на основании первого и второго законов Кирхгофа, всех неизвестных величин, кроме одной, относительно которой и записывается уравнение (2);
- путем использования выражения для входного сопротивления цепи на синусоидальном токе;
- на основе выражения главного определителя.
Согласно первому способу в предыдущей лекции было получено дифференциальное уравнение относительно напряжения 
Следует отметить, что, поскольку линейная цепь охвачена единым переходным процессом, корни характеристического уравнения являются общими для всех свободных составляющих напряжений и токов ветвей схемы, параметры которых входят в характеристическое уравнение. Поэтому по первому способу составления характеристического уравнения в качестве переменной, относительно которой оно записывается, может быть выбрана любая.
Применение второго и третьего способов составления характеристического уравнения рассмотрим на примере цепи рис. 1.
Составление характеристического уравнения по методу входного сопротивления заключается в следующем:
записывается входное сопротивление цепи на переменном токе;
j w заменяется на оператор р;
полученное выражение 
совпадает с характеристическим.
Следует подчеркнуть, что входное сопротивление может быть записано относительно места разрыва любой ветви схемы. При этом активный двухполюсник заменяется пассивным по аналогии с методом эквивалентного генератора. Данный способ составления характеристического уравнения предполагает отсутствие в схеме магнитосвязанных ветвей; при наличии таковых необходимо осуществить их предварительное развязывание.
Для цепи на рис. 1 относительно зажимов источника

Заменив j w на р и приравняв полученное выражение к нулю, запишем
 . . | (1) |
При составлении характеристического уравнения на основе выражения главного определителя число алгебраических уравнений, на базе которых он записывается, равно числу неизвестных свободных составляющих токов. Алгебраизация исходной системы интегро-дифференциальных уравнений, составленных, например, на основании законов Кирхгофа или по методу контурных токов, осуществляется заменой символов дифференцирования и интегрирования соответственно на умножение и деление на оператор р. Характеристическое уравнение получается путем приравнивания записанного определителя к нулю. Поскольку выражение для главного определителя не зависит от правых частей системы неоднородных уравнений, его составление можно производить на основе системы уравнений, записанных для полных токов.
Для цепи на рис. 1 алгебраизованная система уравнений на основе метода контурных токов имеет вид
Отсюда выражение для главного определителя этой системы

Приравняв D к нулю, получим результат, аналогичный (1).
Общая методика расчета переходных процессов классическим методом
В общем случае методика расчета переходных процессов классическим методом включает следующие этапы:
- Запись выражения для искомой переменной в виде
.
(2) - Нахождение принужденной составляющей общего решения на основании расчета установившегося режима послекоммутационной цепи.
- Составление характеристического уравнения и определение его корней (для цепей, описываемых дифференциальными уравнениями первого порядка, вместо корней можно находить постоянную времени t — см. лекцию №26). Запись выражения свободной составляющей в форме, определяемой типом найденных корней.
- Подстановка полученных выражений принужденной и свободной составляющих в соотношение (2).
- Определение начальных условий и на их основе – постоянных интегрирования.
Примеры расчета переходных процессов классическим методом
1. Переходные процессы в R-L цепи при ее подключении к источнику напряжения
Такие процессы имеют место, например, при подключении к источнику питания электромагнитов, трансформаторов, электрических двигателей и т.п.
Рассмотрим два случая:
а)
б) 
Согласно рассмотренной методике для тока в цепи на рис. 2 можно записать
 . . | (3) |
Тогда для первого случая принужденная составляющая тока
 . . | (4) |

откуда 

 . . | (5) |
Подставляя (4) и (5) в соотношение (3), запишем

В соответствии с первым законом коммутации 

откуда 
Таким образом, ток в цепи в переходном процессе описывается уравнением

а напряжение на катушке индуктивности – выражением

Качественный вид кривых 

При втором типе источника принужденная составляющая рассчитывается с использованием символического метода:

где 

Выражение свободной составляющей не зависит от типа источника напряжения. Следовательно,

Поскольку 

Таким образом, окончательно получаем
 . . | (6) |
Анализ полученного выражения (6) показывает:
- При начальной фазе напряжения
постоянная интегрирования А=0. Таким образом, в этом случае коммутация не повлечет за собой переходного процесса, и в цепи сразу возникнет установившийся режим.
- При
свободная составляющая максимальна по модулю. В этом случае ток переходного процесса достигает своей наибольшей величины.
Если 





Таким образом, для линейной цепи максимальное значение тока переходного режима не может превышать удвоенной амплитуды принужденного тока: 
Аналогично для линейной цепи с конденсатором: если в момент коммутации принужденное напряжение равно своему амплитудному значению и постоянная времени 


2. Переходные процессы при отключении катушки индуктивности от источника питания
При размыкании ключа в цепи на рис. 5 принужденная составляющая тока через катушку индуктивности 

откуда 

В соответствии с первым законом коммутации

Таким образом, выражение для тока в переходном режиме
и напряжение на катушке индуктивности
 . . | (7) |
Анализ (7) показывает, что при размыкании цепей, содержащих индуктивные элементы, могут возникать большие перенапряжения, которые без принятия специальных мер могут вывести аппаратуру из строя. Действительно, при 

3. Заряд и разряд конденсатора
При переводе ключа в положение 1 (см. рис. 6) начинается процесс заряда конденсатора:

Принужденная составляющая напряжения на конденсаторе 
Из характеристического уравнения
определяется корень 


При t=0 напряжение на конденсаторе равно 



Соответственно для зарядного тока можно записать

В зависимости от величины 




При разряде конденсатора на резистор 


Тогда, принимая, что к моменту коммутации конденсатор был заряжен до напряжения 


Соответственно разрядный ток
 . . | (8) |
Как видно из (8), во избежание значительных бросков разрядного тока величина 
В заключение отметим, что процессы заряда и разряда конденсатора используются в генераторах пилообразного напряжения, широко применяемых в автоматике. Для этого ключ в схеме на рис. 6 заменяется на электронный.
- Основы теории цепей: Учеб. для вузов /Г.В.Зевеке, П.А.Ионкин, А.В.Нетушил, С.В.Страхов. –5-е изд., перераб. –М.: Энергоатомиздат, 1989. -528с.
- Бессонов Л.А. Теоретические основы электротехники: Электрические цепи. Учеб. для студентов электротехнических, энергетических и приборостроительных специальностей вузов. –7-е изд., перераб. и доп. –М.: Высш. шк., 1978. –528с.
- Теоретические основы электротехники. Учеб. для вузов. В трех т. Под общ. ред. К.М.Поливанова. Т.1. К.М.Поливанов. Линейные электрические цепи с сосредоточенными постоянными. –М.: Энергия- 1972. –240с.
- Составить характеристическое уравнение для цепи на рис. 1, используя выражение входного сопротивления относительно места разрыва ветви с резистором
.
- Может ли в одной части линейной цепи протекать колебательный переходный процесс, а в другой – апериодический?
- Для чего в схеме на рис. 5 служит цепочка, состоящая из диода и резистора R?
- Почему можно разрывать ветвь с конденсатором и нельзя – ветвь с индуктивным элементом?
- Почему корни характеристического уравнения не зависят от того, относительно какой переменной было записано дифференциальное уравнение?
- Для цепи на рис. 8 составить характеристическое уравнение и определить, при каких значениях
переходный процесс в ней будет носить апериодический характер, если
.
Ответ: 
Определить 




Ответ: 
http://toehelp.ru/theory/toe/lecture25/lecture25.html









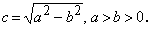












 .
.


 постоянная интегрирования А=0. Таким образом, в этом случае коммутация не повлечет за собой переходного процесса, и в цепи сразу возникнет установившийся режим.
постоянная интегрирования А=0. Таким образом, в этом случае коммутация не повлечет за собой переходного процесса, и в цепи сразу возникнет установившийся режим. свободная составляющая максимальна по модулю. В этом случае ток переходного процесса достигает своей наибольшей величины.
свободная составляющая максимальна по модулю. В этом случае ток переходного процесса достигает своей наибольшей величины.





 .
. переходный процесс в ней будет носить апериодический характер, если
переходный процесс в ней будет носить апериодический характер, если  .
.