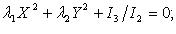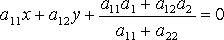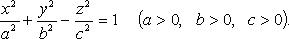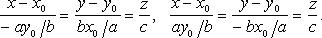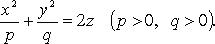Характеристическое уравнение поверхности второй степени
Инварианты общего уравнения поверхности второй степени
Инварианты по отношению к группе ортогональных преобразований:
Характеристическое уравнение поверхности второй степени
его корни
Классификация поверхностей второй степени по числу центров
I группа — имеющие единственный центр симметрии,
II группа — ранга 2 и не имеющие центра симметрии,
III группа — имеющие прямую центров симметрии,
IV группа — ранга 1 и не имеющие центра симметрии,
V группа — имеющие плоскость центров симметрии.
Канонический вид поверхностей второй степени
I группа —
II группа —
III группа —
IV группа —
V группа —
Поверхности второго порядка: их виды, уравнения, примеры
Общее уравнение поверхности второго порядка и инварианты поворота и переноса декартовой прямоугольной системы координат
Общее уравнение поверхности второго порядка имеет вид
Для определения вида поверхности второго порядка по общему уравнению и приведения общего уравнения к каноническому, нам понадобятся выражения, которые называются инвариантами. Инварианты — это определители и суммы определителей, составленные из коэффициентов общего уравнения, которые не меняются при переносе и повороте системы координат. Эти инварианты следующие:
Следующие два выражения, называемые семиинвариантами, являются инвариантами поворота декартовой прямоугольной системы координат:
В случае, если I 3 = 0 , K 4 = 0 , семиинвариант K 3 будет также и инвариантом переноса; в случае же I 3 = 0 , K 4 = 0 , I 2 = 0 , K 3 = 0 семиинвариант K 2 = 0 будет также и инвариантом переноса.
Виды поверхностей второго порядка и приведение общего уравнения поверхности второго порядка к каноническому
I. Если I 3 ≠ 0 , то общее уравнение поверхности второго порядка при помощи поворота и переноса прямоугольной системы координат может быть приведено к следующему виду:

где λ 1 , λ 2 , λ 3 — корни характеристического уравнения

В зависимости от того, какие знаки у чисел λ 1 , λ 2 , λ 3 и K 4 /I 3 , определяется вид поверхности второго порядка.
Эллипсоид
Если числа λ 1 λ 2 , λ 3 одного знака, а K 4 /I 3 имеет знак им противоположный, то общее уравнение поверхности второго порядка определяет эллипсоид.
После решения характеристического уравнения общее уравнение можно переписать в следующем виде:

Тогда полуоси эллипсоида будут



Поэтому каноническое уравнение эллипсоида имеет вид

Мнимый эллипсоид
Если числа λ 1 λ 2 , λ 3 и K 4 /I 3 одного знака, то общее уравнение поверхности второго порядка определяет мнимый эллипсоид.
После решения характеристического уравнения общее уравнение можно привести к каноническому уравнению мнимого эллипсоида:




Мнимый конус
Если числа λ 1 λ 2 , λ 3 , а K 4 = 0 , то общее уравнение поверхности второго порядка определяет мнимый конус.
После решения характеристического уравнения общее уравнение можно привести к каноническому уравнению мнимого конуса:




Однополостный гиперболоид
Если два корня характеристического уравнения имеют один знак, а третий корень и K 4 /I 3 имеют знак, им противоположный, то общее уравнение поверхности второго порядка определяет однополостный гиперболоид.
Обозначая в этом случае через λ 1 и λ 2 корни характеристического уравнения, имеющие один знак, общее уравнение можно переписать в виде:




то каноническое уравнение однополостного гиперболоида будет иметь вид

Двуполостный гиперболоид
Если два корня характеристического уравнения и K 4 /I 3 имеют один и тот же знак, а третий корень характеристического уравнения им противоположный, то общее уравнение поверхности второго порядка определяет двуполостный гиперболоид.
Обозначая в этом случае через λ 1 и λ 2 корни, имеющие один знак, общее уравнение можно переписать в виде:

Последняя запись и есть каноническое уравнение двуполостного гиперболоида.
Конус
Если два корня характеристического уравнения имеют один знак, третий корень имеет знак, им противоположный, а K 4 = 0 , то общее уравнение поверхности второго порядка определяет конус.
Считая, что одинаковый знак имеют корни λ 1 и λ 2 , общее уравнение можно переписать в виде:

известном как каноническое уравнение конуса.
II. Если I 3 = 0 , а K 4 ≠ 0 , то общее уравнение поверхности второго порядка при помощи поворота и переноса прямоугольной системы координат может быть приведено к следующему виду:

где λ 1 и λ 2 — отличные от нуля корни характеристического уравнения.
Эллиптический параболоид
Если λ 1 и λ 2 имеют один знак, то общее уравнение поверхности второго порядка определяет эллиптический параболоид.
Общее уравнение можно переписать в виде:

Выбирая перед корнем знак, противоположный знаку λ 1 и λ 2 , и полагая


получим каноническое уравнение эллиптического параболоида:

Гиперболический параболоид
Если λ 1 и λ 2 имеют разные знаки, то общее уравнение поверхности второго порядка определяет гиперболический параболоид.
Обозначая через λ 1 положительный корень, а через λ 2 — отрицательный и беря перед корнем 



получим каноническое уравнение гиперболического параболоида:

III. Если I 3 = 0 , а K 4 = 0 , I 2 ≠ 0 то общее уравнение поверхности второго порядка при помощи поворота и переноса прямоугольной системы координат может быть приведено к следующему виду:

где λ 1 и λ 2 — отличные от нуля корни характеристического уравнения.
Эллиптический цилиндр
Если λ 1 и λ 2 одного знака, а K 3 /I 2 имеет знак, им противоположный, то общее уравнение поверхности второго порядка определяет эллиптический цилиндр.
Переписываем уравнение, получившееся после решения характеристического уравнения, в виде:



получим каноническое уравнение эллиптического цилиндра:

Мнимый эллиптический цилиндр
Если λ 1 , λ 2 и K 3 /I 2 одного знака, то общее уравнение поверхности второго порядка определяет мнимый эллиптический цилиндр.
Переписываем уравнение, получившееся после решения характеристического уравнения, в виде:

Последняя запись — каноническое уравнение мнимого эллиптического цилиндра.
Мнимые пересекающиеся плоскости
Если λ 1 и λ 2 имеют один знак, а K 3 = 0 , то общее уравнение поверхности второго порядка определяет две мнимые пересекающиеся плоскости.
Переписываем уравнение, получившееся после решения характеристического уравнения, в виде:



получим каноническое уравнение мнимых пересекающихся плоскостей:

Гиперболический цилиндр
Если λ 1 и λ 2 имеют разные знаки, а K 3 ≠ 0 , то общее уравнение поверхности второго порядка определяет гиперболический цилиндр.
Переписываем уравнение, получившееся после решения характеристического уравнения, в виде:



Таким образом, каноническое уравнение гиперболического цилиндра:

Пересекающиеся плоскости
Если λ 1 и λ 2 имеют разные знаки, а K 3 = 0 , то общее уравнение поверхности второго порядка определяет две пересекающиеся плоскости.
Переписываем уравнение, получившееся после решения характеристического уравнения, в виде:



Таким образом, пересекающихся плоскостей:

IV. Если I 3 = 0 , K 4 = 0 , I 2 = 0 , K 3 ≠ 0 , то общее уравнение поверхности второго порядка при помощи поворота и переноса прямоугольной системы координат может быть приведено к следующему виду:

где λ 1 = I 1 — отличный от нуля корень характеристического уравнения.
Параболический цилиндр
Уравнение, получившееся после решения характеристического уравнения, можно переписать в виде:


Это уравнение параболического цилиндра, в каноническом виде оно записывается так:

V. Если I 3 = 0 , K 4 = 0 , I 2 = 0 , K 3 = 0 , то общее уравнение поверхности второго порядка при помощи поворота и переноса прямоугольной системы координат может быть приведено к следующему виду:


Параллельные плоскости
Если K 2 , то общее уравнение поверхности второго порядка определяет две параллельные плоскости.

перепишем его в виде

Мнимые параллельные плоскости
Если K 2 > 0 , то общее уравнение поверхности второго порядка определяет две мнимые параллельные плоскости.

перепишем его в виде

Совпадающие плоскости
Если K 2 = 0 , то общее уравнение поверхности второго порядка определяет две совпадающие плоскости:

Решение примеров на определение вида поверхности второго порядка
Пример 1. Определить вид и составить каноническое уравнение поверхности, заданной относительно прямоугольной системы координат общим уравнением
Решение. Найдём I 3 :

I 1 = 1 + 5 + 1 = 7 ,
Следовательно, данная поверхность — однополостный гиперболоид.

Составляем и решаем характеристическое уравнение:






Пример 2. Определить вид и составить каноническое уравнение поверхности, заданной относительно прямоугольной системы координат общим уравнением
Решение. Найдём I 3 :


Следовательно, общее уравнение определяет эллиптический параболоид.

I 1 = 2 + 2 + 3 = 7 .
Решаем характеристическое уравнение:





Пример 3. Определить вид и составить каноническое уравнение поверхности, заданной относительно прямоугольной системы координат общим уравнением



I 1 = 5 + 2 + 5 = 12 .
Так как I 3 = К 4 = 0 , I 2 > 0 , I 1 K 3 , то данное общее уравнение определяет эллиптический цилиндр.


Определить вид поверхности второго порядка самостоятельно, а затем посмотреть решение
Пример 4. Определить вид и составить каноническое уравнение поверхности, заданной относительно прямоугольной системы координат общим уравнением
Характеристическое уравнение линии второй степени
его корни
Классификация линий второй степени по числу центров
I группа — имеющие единственный центр симметрии,
II группа — не имеющие центра симметрии,
III группа — имеющие прямую центров симметрии.
Канонический вид линий второй степени
I группа:
II группа:
III группа:
Необходимые и достаточные признаки линий второй степени
Расположение эллипса и гиперболы относительно исходной системы координат
Координаты нового начала (центра) — решение системы
Угловой коэффициент новой оси 

Расположение параболы относительно исходной системы координат
Координаты вершины — решение системы, определяемой уравнением параболы и уравнением ее оси:
Параметр параболы:
Направляющий вектор оси (в сторону ее вогнутости):
Поверхности второй степени
Канонические уравнения
Сфера
Сфера радиуса R с центром в начале координат:
Сфера радиуса R с центром в точке S (a; b; c):
Эллипсоид (рис. 4.18)




Сечения эллипсоида плоскостями — либо эллипс (окружность), либо точка, либо 
Конус второй степени (рис. 4.19)
a = b — конус вращения (прямой круговой).
Сечения конуса плоскостями: в плоскости, пересекающей все прямолинейные образующие, — эллипс; в плоскости, параллельной одной прямолинейной образующей, — парабола; в плоскости, параллельной двум прямолинейным образующим, — гипербола; в плоскости, проходящей через вершину конуса, — пара пересекающихся прямых или точка (вершина).
Однополостный гиперболоид (рис. 4.20)
a = b — однополостный гиперболоид вращения вокруг оси Oz.
Горловой эллипс:
Асимптотический конус:
Сечения однополостного гиперболоида плоскостями — либо эллипс, либо парабола, либо гипербола, либо пара прямых (прямолинейных образующих).
Прямолинейные образующие
Через произвольную точку 


В частности, если точку 

Двуполостный гиперболоид (рис. 4.21)
a = b — двуполостный гиперболоид вращения вокруг оси Oz.
Сечения двуполостного гиперболоида плоскостями: либо эллипс, либо гипербола, либо парабола, либо точка, либо 
Эллиптический параболоид (рис. 4.22)
p = q — параболоид вращения вокруг оси Oz.
Сечения эллиптического параболоида плоскостями — либо эллипс, либо парабола, либо точка, либо 
Гиперболический параболоид (рис. 4.23)
Сечения гиперболического параболоида плоскостями — либо гипербола, либо парабола, либо пара прямых (прямолинейных образующих).
Прямолинейные образующие
Через каждую точку 
Эллиптический цилиндр (рис. 4.24)
при a = b — круговой цилиндр.
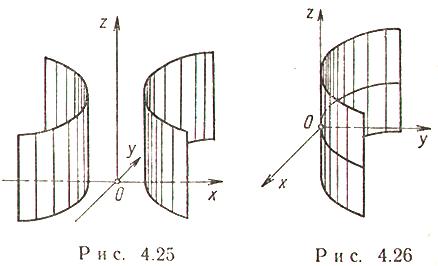
Гиперболический цилиндр (рис. 4.25)
Параболический цилиндр (рис. 4.26)
http://function-x.ru/surfaces_of_the_second_order.html
http://lektsii.org/8-59929.html