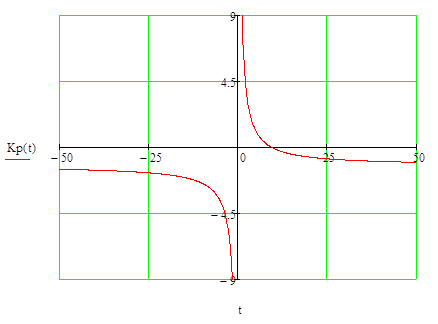
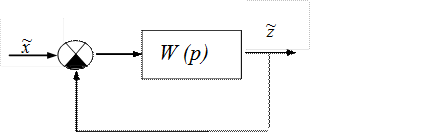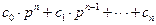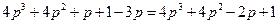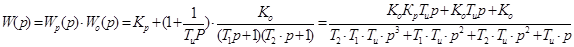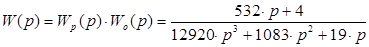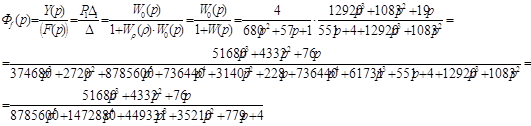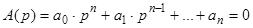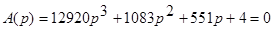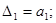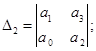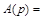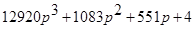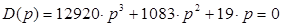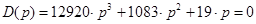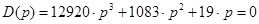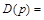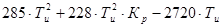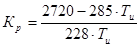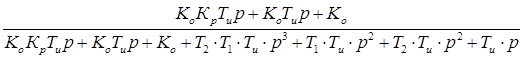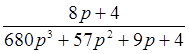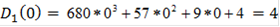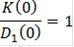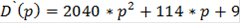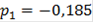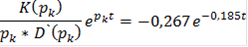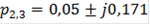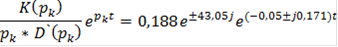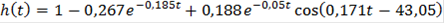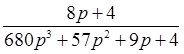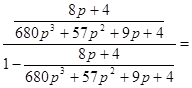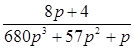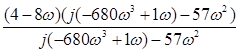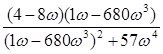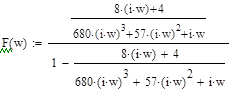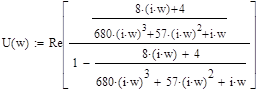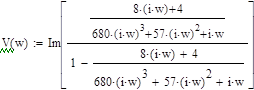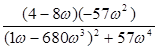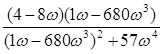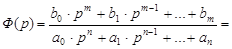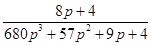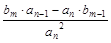II.7.Характеристические уравнения САР
Рассмотрим замкнутую САР (рис.II.27). Возьмём для определённости САР с единичной отрицательной обратной связью (получение характеристических уравнений для других случаев, например, с неединичной или положительной обратными связями принципиально ничем не отличается от рассмотренного ниже).
Рис. II.27. Замкнутая САР.
Передаточная функция рассматриваемой системы имеет вид
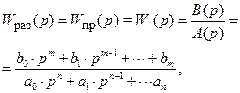
причём для реальных технических систем n ≥ m. Передаточная функция разомкнутой системы играет весьма большое роль в теории автоматического регулирования, т.к. многие методы анализа и синтеза основаны на использовании именно этой характеристики.
Для замкнутой САР, изображённой на рис.II.27, передаточная функция имеет вид
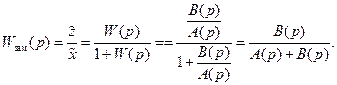
Полиномы знаменателя (вспомним II.3.3) передаточной функции разомкнутой системы (II.7.1)
А(р) =
и передаточной функции замкнутой системы (II.7.2)
А(р)+В(р)= = 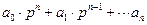
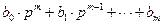
называются характеристическими полиномами. Поскольку n ≥ m, то порядок полинома А(р) + В(р) останется прежним, равным n, т.е. таким же,чтои у А(р), только коэффициенты полинома замкнутой системы ci будут отличаться от коэффициентов разомкнутой системы ai. В дальнейшем характеристический полином любой системы (замкнутой или разомкнутой) будем представлять в виде
D(p) = 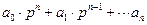
Например, если 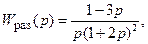
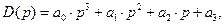
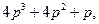
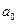
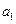
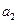
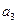

коэффициенты характеристического уравнения примут значения 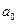
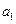
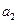
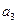
Приравнивание нулю полинома (II.7.3) даёт характеристическое уравнение системы
D(p) = 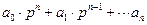
Такое название это уравнение получило потому, что оно характеризует, определяет переходный процесс в системе, т.е. динамику САР.
Характеристическое уравнение замкнутой САУ
ЗАДАНИЯ НА КОНТРОЛЬНУЮ РАБОТУ
|
1. Исследовать одноконтурную САУ при заданных передаточных функциях составляющих ее элементов.
|
|
|
|
Рис. 1.1 Структура одноконтурной САУ
регулятора, исполнительного механизма, объекта регулирования, датчика соответственно.
φ, φ3, φg — заданное, действительное и измеренное значения регулируемой величины соответственно;
λ — возмущающее воздействие.
При выполнениии задания вид передаточных функций определяют по последней цифре номера зачетной книжки, а значения коэффициентов по предпоследней.
Таблица 1.1
Значения передаточных функций звеньев САУ
| №/пп | Wн(p) | Wc(p) | Wp(p) | Wo(p) |
 |  |  |  | |
 |  |  |  | |
 |  |  |  | |
 |  |  |  | |
 |  |  |  | |
 |  |  |  | |
 |  | 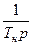 |  | |
 |  |  |  | |
 |  |  |  | |
 |  |  |  |
Таблица 1.2
Значения коэффициентов передаточных функций
| № | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| Kо | 1,6 | 1,1 | 1,8 | 2,1 | 1,6 | 1,9 | 2,8 | 3,2 | 1,4 | 0,9 |
| То | ||||||||||
| Т | ||||||||||
| Kр | ||||||||||
| Тн | ||||||||||
| Тg | ||||||||||
| Kс | 0,1 | 0,4 | 0,3 | 0,7 | 0,9 | 1,8 | 1,2 | 0,9 | 2,0 | 1,7 |
| Тс | ||||||||||
| Ни | 1,2 | 1,2 | 1,2 | 1,2 | 1,2 | 1,2 | 1,2 | 1,2 | 1,2 | 1,2 |
| Т1 |
1.1. Рассчитать передаточные функции разомкнутой и замкнутой САУ по каналам возмущающего воздействия λ и задания φ3.
1.2. Выполнить анализ устойчивости замкнутой системы с применением алгебраического и частотного критериев устойчивости.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
Передаточные функции соединения звеньев САУ

Рис. 2.1 Последовательное соединение звеньев САУ
Результирующая передаточная функция равна отношению операторного изображения выходной величины к операторному изображению входной при нулевых начальных условиях

При параллельном включении звенья имеют общий вход, а выходной сигнал цепочки равен сумме выходных сигналов отдельных звеньев.
Рис. 2.2 Параллельное соединение звеньев САУ
Для этой схемы результирующая передаточная функция равна сумме передаточных функций отдельных звеньев и имеет вид:

Для замкнутых САУ характерно так называемое встречно-параллельное включение или соединение с обратной связью.
Рис. 2.3 Соединение с обратной связью
В этом случае результирующая передаточная функция равна дроби, числитель которой передаточная функция прямой связи, а знаменатель — единица плюс или минус передаточная функция разомкнутого контура. Знак плюс соответствует отрицательной, а минус — положительной обратной связи.

Под прямой связью понимается передаточная функция между искомыми переменными по направлению прохождения сигнала без учета главной обратной связи. В рассматриваемой схеме передаточная функция прямой связи между λ и φ равна Wo(p), а между φ3 и φ – Wp(p)Wc(p)Wo(p). Передаточная функция прямой связи между φ3 и ε равна единице. Поэтому
где 


Выполняя несложные преобразования, определим

Для замкнутой системы передаточная функция по каналу 

Характеристическое уравнение замкнутой САУ
Для анализа устойчивости САУ необходимо знать характеристическое уравнение замкнутой системы. Оно получается, если приравнять знаменатель передаточной функции замкнутой системы нулю, т.е.
Известно правило, что при известной передаточной функции разомкнутой системы, характеристическое уравнение замкнутой системы получают сложением полиномов числителя и знаменателя и приравниванием полученной суммы нулю, A(p)+B(p)=0
В рассматриваемом примере (2.4)
Сложив их, получают в общем виде характеристическое уравнение замкнутой системы:
Оценка устойчивости замкнутой системы алгебраическим и частотным методами
РЕФЕРАТ
Курсовая работа содержит рисунков 7 , страниц 25 . В работе рассмотрена линейная непрерывная система автоматического регулирования. Различными методами исследована устойчивость системы, проведена оценка запаса устойчивости. Также проведена оценка качества системы с использованием различных показателей качества.
ОГЛАВЛЕНИЕ
Лист для замечаний
. Передаточная функция разомкнутой системы
. Определение передаточной функции замкнутой системы
. Оценка устойчивости замкнутой системы алгебраическим и частотным методами
. Построение области устойчивости системы в плоскости параметров
. Выбор параметров системы из области устойчивости и вычисление ее статистической погрешности
. Построение переходного процесса ошибке от задающего воздействия
Всякий технологический процесс характеризуется определенными физическими величинами. Ими могут быть температура, давление, уровень, концентрация и так далее. Для обеспечения требуемого режима работы эти величины необходимо поддерживать постоянными или изменяющимися по какому — либо закону. Отсюда необходимость использования специальных автоматических устройств и систем управления. Функцию автоматического управления выполняет система автоматического управления.
В зависимости от назначения САУ могут быть разбиты на САР и кибернетические системы. САР решает задачу регулирования, т. е. обеспечивает изменение физической величины по требуемому закону, без участия человека. К задачам кибернетических систем относятся самонастройка и самоорганизация, каких — либо систем, выбора лучших режимов работы и так далее. Автоматическое устройство, предназначенное для выполнения задачи регулирования называется автоматическим регулятором. Несмотря на разнообразие технологических процессов, построение автоматических систем основывается на ряде общих принципов. К ним относятся принцип регулирования по отклонению, принцип регулирования по возмущению, комбинированное регулирование, принцип адаптации. Принцип регулирования определяет на основе какой информации формируется регулирующее воздействие.
1.
Передаточная функция разомкнутой системы
N(p) =
Общий вид передаточной функции:

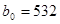
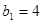
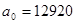
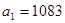
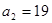
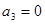
Разомкнутая система является устойчивой(для систем 3,4 порядка необходимо и достаточно для условия устойчивости системы имение положительных корней), а также имеется нулевой корень, следовательно система находится на границе устойчивости.
Определение передаточной функции замкнутой системы:
а) по задающему воздействию:
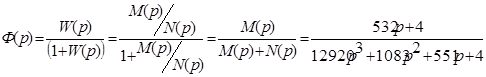
б) по возмущающему воздействию:
в) по ошибке от задающего воздействия:
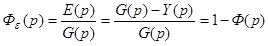

Оценка устойчивости замкнутой системы алгебраическим и частотным методами
Для замкнутой системы:
Характеристическое уравнение замкнутой системы имеет вид:
а) с помощью критерия Рауса-Гурвица:
Этот критерий относится к алгебраическим критериям, накладывающим ограничения на коэффициенты характеристического уравнения. Он был предложен английским математиком Раусом в 1845 году, а затем вновь выведен и дополнен Гурвицем в 1893 году.
Рассмотрим этот критерий:
Пусть характеристическое уравнение имеет вид:
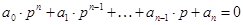
причем а0 > 0 (1), тогда для устойчивости линейной САР необходимо и достаточно, чтобы были положительными главный определитель Гурвица и все его диагональные миноры, т.е. при а0 > 0, 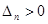
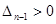

Диагональные миноры (определители Гурвица) представляют собой диагональные определители квадратной матрицы Гурвица F полного порядка n, составленной из коэффициентов уравнения (1).

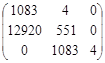
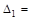
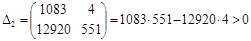

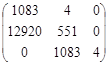




Таким образом, согласно критерию Рауса-Гурвица замкнутая система устойчива, т.к. все коэффициенты и главный определитель положительны.
б) с помощью критерия Михайлова:
Этот критерий принадлежит к числу частотных критериев и позволяет судить об устойчивости замкнутой системы по виду годографа построенного с помощью характеристического уравнения
В характеристическом уравнении проведем замену p на jw:
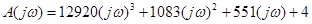
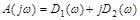
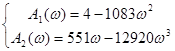
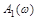
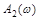
Начальная точка (4;0)
При 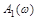
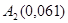
При 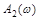
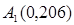
Рисунок 2- Кривая Михайлова (годограф), для замкнутой системы
Вывод: замкнутая система устойчива, т.к. годограф Михайлова, при изменении частоты w от 0 до ∞, начав свое движение с положительной действительной оси и вращаясь против часовой стрелки, последовательно проходит 3 квадранта, нигде не обращаясь в нуль (степень характеристического уравнения n=3).
Для разомкнутой системы:
0 = 12920; a1 = 1083; a2 = 19 ; a3 = 0; n = 3.
а) с помощью критерия Рауса — Гурвица для разомкнутой САР:
Матрица Гурвица для характеристического уравнения


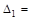
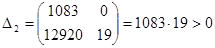
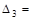
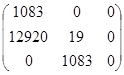
Таким образом, согласно критерию Рауса-Гурвица разомкнутая САР находится на границе устойчивости, т.к. a0 > 0, определители первого и второго порядков положительны, а определитель третьего порядка равен 0.
б) с помощью критерия Михайлова:
Этот критерий принадлежит к числу частотных критериев и позволяет судить об устойчивости замкнутой системы по виду гадографа, построенного с помощью характеристического уравнения:
В характеристическом уравнении проведем замену p на j∙ω, в результате получаем функцию комплексной переменной, представляющую собой характеристический вектор:
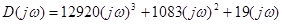
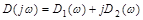
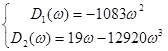

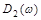
Начальная точка (0;0)
При 
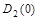
При 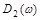
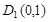
Рисунок 3- Кривая Михайлова (годограф), для разомкнутой системы
Вывод: разомкнутая система будет находиться на границе апериодической устойчивости, т.к. имеется нулевой корень, и годограф Михайлова начинает своё движение из начала координат.
3. Построение области устойчивости системы в плоскости параметров К0 , Ти. Использовать методы Д-разбиения и критерий Рауса-Гурвица
Для выделения области параметров, обеспечивающих устойчивую работу САУ, используют критерий устойчивости.
а) с помощью критерия Рауса — Гурвица
Для выделения области, обеспечивающей устойчивость САУ, запишем все условия устойчивости. Это положительность всех главных миноров до n-1 при а0 > 0. При равенстве нулю минора, получаем границу устойчивости.
A(p) = 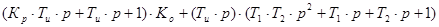
= 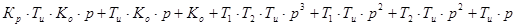
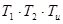
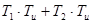
Составим неравенство для коэффициентов и миноров:
0 = 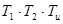


a1 = 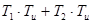
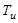
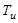
a2 = 


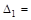
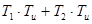
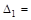
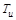
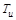

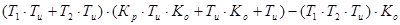





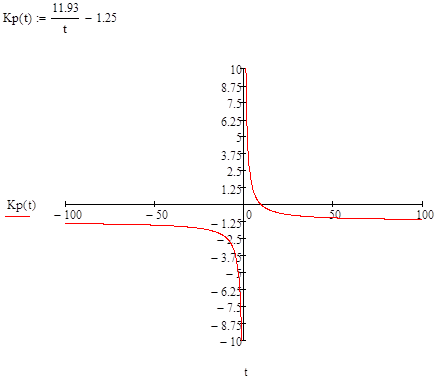
Рисунок 4 — Определение области устойчивости (Гурвиц)
б) с помощью критерия Михайлова
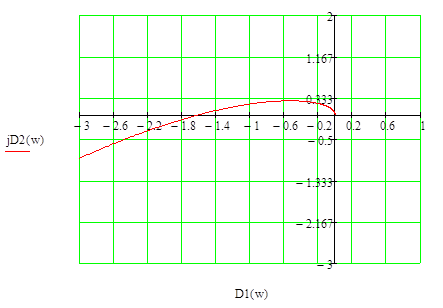
По критерию Михайлова если система находится на колебательной границе устойчивости, то годограф проходит через начало координат при ω≠0.
Если характеристический вектор замкнутой системы имеет вид
D(jω)= D1(ω)+jD2(ω), то уравнение границы устойчивости можно получить, решив систему уравнений:
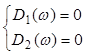
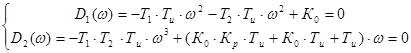
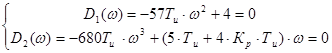
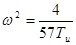
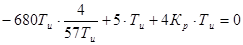
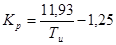
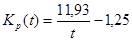
Рисунок 5 — Определение области устойчивости (Михайлов)
4. Построение переходного процесса замкнутой системы по задающему воздействию
Ф(p) =
Выбрав параметры САР из области устойчивости, Кр = 1,Ти = 1
Ф(p) =
H(p) = Ф(p)/p =
Приведем выражение к сумме табличных функций. Для этого представим паленом знаменателя в виде:
(p-p1) (p-p2) (p-p3), где p1 p2 p3 — корни паленома
Согласно теореме разложения:
Находим значения из формулы:
Подставляем найденные значения корней в выражение 

Подставляем найденные значения в исходную формулу, получим:
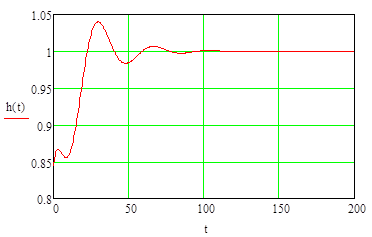
Строим получившуюся функцию:
Рисунок 6. График построения процесса замкнутой системы по задающему воздействию.
5.
Запасы устойчивости замкнутой системы по модулю и фазе
Выполнение требований устойчивости САР является необходимым, но недостаточным условием. При расчетах САР требуется, чтобы система была не только устойчива, но и обладала определенным запасом устойчивости.
Запас устойчивости системы по модулю, это длина отрезка h, равная расстоянию от точки пересечения АФХ разомкнутой системы и отрицательной вещественной полуоси до точки (0;j0). Численно запас устойчивости по модулю показывает, на сколько должен измениться модуль АФХ разомкнутой системы на частоте, при которой φ(ωπ)=-180̊ для выхода системы на границу устойчивости.
Запас устойчивости системы по фазе — это угол φ, который лежит между вещественной отрицательной полуосью и лучом, проведенным из начала координат в точку пересечения АФХ с окружностью единственного радиуса с центром в начале координат. Численно запас устойчивости системы по фазе показывает, на сколько должно увеличиться отставание по фазе в разомкнутой системе на частоте wcp, при которой АЧХ = 1 для выхода системы на границу устойчивости.
система автоматический регулирование передаточный
Ф(p) =
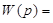
Выполним подстановку p=jω и представим W(jω) в виде W(jω) = U(ω)+jV(ω), тогда:
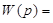

= 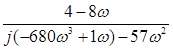
U(ω) = 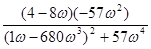
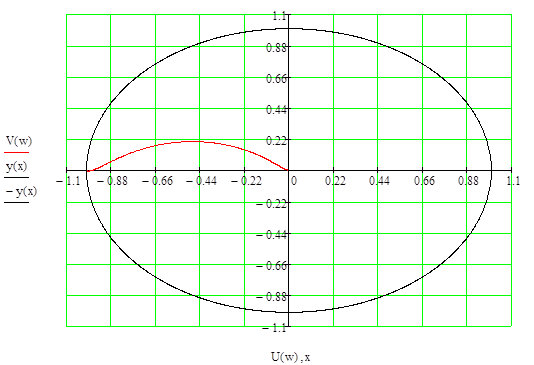
Рисунок 7. Определение запаса устойчивости системы.
Найдем точку пересечения графиков. Для этого решим систему уравнений:
=
y =
Запас устойчивости системы по модулю:
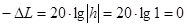
Запас устойчивости системы по фазе
Вывод: система автоматического регулирования находиться на границе устойчивости, запаса устойчивости САР не имеет, что не гарантирует сохранение устойчивости при изменении параметров.
6. Оценка качества замкнутой системы с помощью интегральных и корневых методов
Устойчивость САР является необходимым условием её работоспособности, однако, это условие не обеспечивает всех требований, предъявляемых к работе системы. Во многих случаях требуется, чтобы система за строго определенное время переходила из одного устойчивого состояния в другое или чтобы система достаточно точно воспроизводила задающие воздействия, несущие информацию об изменении регулируемых переменных.
На практике применяют прямые и косвенные методы исследования качества процессов регулирования. Если показатели качества определяются непосредственно по кривой переходного процесса, то они называются прямыми показателями качества.
Прямые оценки качества определяют по кривой переходной функции h(t), полученной при g(t)=l(t). Переходные процессы при ступенчатых воздействиях делят на монотонные, апериодические и колебательные.
Время регулирования tp или время переходного процесса — это время от момента начала изменения входного воздействия до момента, когда абсолютная разность между текущим и установившимся значением регулируемой величины будет оставаться меньше некоторого заданного значения ∆.
при t > tp ∆ = (0,03…0,05) hуст
Перерегулирование или выброс, представляет собой максимальное отклонение регулируемой переменной от нового установившегося значения. Перерегулирование характеризует плавность протекания процесса.
σ = (hmax-hуст) / hуст *100%
Т.к. hуст = 1 , hmax=1,04 , σ = 4%
Число колебаний характеризует колебательность переходного процесса, определяется числом максимумов кривой переходного процесса за время регулирования.
Косвенными оценками называются некоторые числа, характеризующие отдельные стороны переходного процесса. Они подразделяются на корневые, частотные, интегральные. В основе корневых методов лежит изучение влияния на процесс регулирования расположения корней характеристического уравнения на комплексной плоскости. Наиболее распространенной является оценка быстроты затухания переходного процесса по степени устойчивости.
Под степенью устойчивости η понимается абсолютное значение вещественной части ближайшего к мнимой оси корня, т.е.
Выбираем самый маленький по модулю корень η = 0,05.
Составляющая в переходном процессе, определяемая парой комплексных корней будет y(t) = Cηe-ηt sin(βt+ψ).
При sin(βt+ψ) = 1 найдем время регулирования:
tp≤ 
где m = 0,05 некоторая числовая характеристика, показывающая во сколько раз уменьшается регулируемая величина за время tp.
Коэффициент затухания α — вещественная часть корня, угловая частота колебаний — мнимая часть корня. Тогда степень затухания будет определяться как
φ = 1 — е-2πα/β = 1 — е-2*3,14*0,025/0,156 = 0,841
Рассмотрим понятие среднегеометрического корня:
Ω0 = 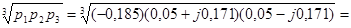
Величина Ω0 зависит от свободного члена an исходного характеристического уравнения, который определяется коэффициентом передачи К разомкнутой системы:
Найдем меру колебательной системы μ:
μ = tg |0,171/0,05| = 0,06
Интегральные методы дают общую оценку переходного процесса, не выделяя те или иные показатели качества, например быстродействие, колебательность и т.д.
Чем меньше I1 — интегральная оценка, тем выше качество системы.
Передаточная функция замкнутой системы:
I 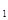
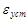
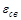
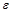
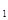
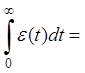

I1 = 
Главная цель курсовой работы состояла в исследовании системы автоматизированного регулирования, ее основных и важнейших параметров. Большое внимание было уделено устойчивости системы, определению границ, а также запаса устойчивости исследованной САР. Устойчивость является одной из основных динамических характеристик САР. Под устойчивостью понимается свойство системы возвращаться к состоянию установившегося равновесия после устранения возмущения, нарушившего равновесие. Определены передаточные функции разомкнутой САР и замкнутой системы по каналу задающего, возмущающего воздействий. С помощью критерия Рауса-Гурвица и критерия Михайлова было установлено, что система является устойчивой, и была построена область устойчивости системы в плоскости параметров Kр, Tи.
Для построения переходного процесса замкнутой системы по задающему воздействию мы выбрали точку из области устойчивости, однако близкую к границе устойчивости. Определили запас устойчивости системы по модулю 0 дб. Так как разомкнутая система не имеет запас устойчивости, можно сделать вывод, что замкнутая система возможно будет устойчива.
Также в данной курсовой работе были рассмотрены два метода оценки качества работы сситемы — интегральный и корневой. Качество процессов регулирования — комплекс требований, определяющих поведение системы в установившемся и переходном режимах при заданном воздействии. Простейшей интегральной оценкой является линейная интегральная оценка. Соответственно чем меньше эта величина, тем выше качество системы. В основе корневых методов лежит изучение влияния на процесс регулирования расположения корней характеристического уравнения на комплексной плоскости.
1. Коряковская Н.В. Методические указания к выполнению курсовой работы. — Архангельск.2002;
. Бесекерский А.В., Попов Е.П. Теория систем автоматического регулирования, Изд-во «Наука», Главная редакция физико-математической литературы, М., 1972, 768 с;
. Шульгин В.А. Методические указания к выполнению курсовой работы.
http://poisk-ru.ru/s10949t3.html
http://megalektsii.ru/s64355t13.html