Идеальная жидкость уравнение бернулли следствия из уравнения бернулли

Тема 3. Кинематика и динамика жидкостей и газов, Лекция 11. Уравнение Бернулли и следствия из него

Тема 3. Кинематика и динамика жидкостей и газов

Лекция 11. Уравнение Бернулли и следствия из него

1. Основные положения гидродинамики. Уравнение неразрывности струи.

2. Уравнение Бернулли.

3. Истечение жидкости из отверстия. Принцип реактивного движения.

ОТВОДИМОЕ ВРЕМЯ: 2 часа.

1. Суханов курс физики. — М.: 1996.

2. Савельев общей физики. Том 1. — M: — Наука, 1996. § 72,73,74.

3. Трофимова физики. – М.: Высшая школа, 1999. § 28,29,30.

4. , Детлаф по физике. — М.: Наука, 1996. Отдел III.

Современные летательные аппараты способны выполнять саше разнообразные задачи и осуществлять полет в различных физических условиях. Физическими условиями полета называется совокупность фи­зических свойств атмосферы и физических явлений, возникающих во время полета летательных аппаратов. Физические условия полета оп­ределяются, в первую очередь, назначением летательного аппарата и могут значительно, а порой и быстро, изменяться в процессе полета. Ярким примером являются пилотируемые космические корабли многора­зового использования, способные осуществлять полет как в околозем­ном космическом пространстве, т. е. в практически безвоздушном пространстве, так и в нижних плотных слоях атмосферы.

В безвоздушном пространстве полет летательных аппаратов осно­ван на реактивном принципе движения, т. е. на законах движения тел с переменной массой, вытекающих из основных законов динамики поступательного движения твердых тел.

Полет летательных аппаратов в воздушной среде подчиняется за­конам аэродинамики, начало которой положено трудами русского уче­ного () и его ученика . В основе аэродинамики, как науки, лежит гидродинамика — физическая теория движения несжимаемых жидкостей с твердыми телами.

Основные положения и выводы гидродинамики применимы не только к жидкостям, но и к газам в том случае, когда сжимаемостью их мож­но пренебречь. Соответствующие расчеты показывают, что при движе­нии жидкостей и газов со скоростями меньшими скорости звука, их с достаточной степенью точности можно считать несжимаемыми. Следова­тельно, движение твердых тел, в том числе летательных аппаратов, в воздушной среде при указанных Скоростях подчиняется законам гидро­динамики.

Для выяснения физической сущности процессов, определяющих по­лет летательных аппаратов, необходимо уяснить основные положения гидродинамики.

1. ОСНОВНЫЕ ПОЛОЖЕНИЯ ГИДРОДИНАМИКИ. УРАВНЕНИЕ НЕРАЗРЫВНОСТИ СТРУИ

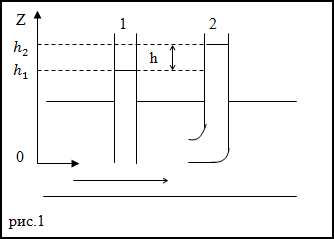
Движение жидкостей называется течением, а совокупность частиц движущейся жидкости потоком. Графически движение жидкостей изображается с помощью линий, которые проводятся так, что касательные к ним совпадают по направлению с вектором скорости жидкости в соответствующих точках пространства (рис. 1).

Линии тока проводятся так, чтобы густота их, характеризуемая отношением числа линий к площади перпендикулярной им площадки, через которую они проходят, была больше там, где больше скорость течения жидкости, и меньше там, где жидкость течет медленнее. Таким образом, по картине линий тока можно судить о направлении и модуле скорости в разных точках пространства, т. е. можно определить состояние движения жидкости. Линии тока в жидкости можно «проявить», например, подмешав в нее какие-либо заметные взвешенные частицы.

Часть жидкости, ограниченную линиями тока, называют трубкой тока.

Течение жидкости называется установившимся (или стационарным), если форма и расположение линий тока, а также значения скоростей в каждой ее точке со временем не изменяются.

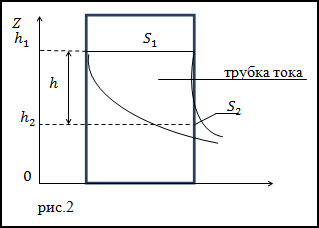
Рассмотрим какую-либо трубку тока. Выберем два ее сечения S1 и S2, перпендикулярные направлению скорости (рис. 2).

За время Δt через сечение S проходит объем жидкости SvΔt; следовательно, за 1с через S1 пройдет объем жидкости S1v1, где v1 — скорость течения жидкости в месте сечения S1. Через сечение S2 за 1с пройдет объем жидкости S2v2, где v2 — скорость жидкости в месте сечения S2. Здесь предполагается, что скорость жидкости в сечении постоянна. Если жидкость несжимаема (ρ=const), то через сечение S2 пройдет такой же объем жидкости, как и через сечение S1, т. е.

Следовательно, произведение скорости течения несжимаемой жидкости на поперечное сечение трубки тока есть величина постоянная для данной трубки тока. Соотношение 1 называется уравнением неразрывности для несжимаемой жидкости.

2. УРАВНЕНИЕ БЕРНУЛЛИ

Выделим в стационарно текущей идеальной жидкости (физическая абстракция, т. е. воображаемая жидкость, в которой отсутствуют силы внутреннего трения) трубку тока, ограниченную сечениями S1 и S2, по которой слева направо течет жидкость (рис. 3).

Пусть в месте сечения S1 скорость течения v1 давление Р1 и высота, на которой это сечение расположено, h1. Аналогично, в месте сечения S2 скорость течения v2, давление Р2 и высота сечения h2. За малый промежуток времени Δt жидкость перемещается от сечения S1 к сечению S’1, от S2 к S’2.

Согласно закону сохранения энергии, изменение полной энергии E2-E1 идеальной несжимаемой жидкости должно быть равно работе А внешних сил по перемещению массы жидкости:

где E1 и Е2 — полные энергии жидкости массой m в местах сечений S1 и S2 соответственно.

С другой стороны, А — это работа, совершаемая при перемещении всей жидкости, заключенной между сечениями S1 и S2, за рассматриваемый малый промежуток времени Δt. Для перенесения массы m от S1 до S’1 жидкость должна переместиться на расстояние l1 =v1 Δt и от S2 до S’2 — на расстояние l2 =v2 Δt. Отметим, что 11 и 12 настолько малы, что всем точкам объемов, закрашенных на рис. 3, приписывают постоянные значения скорости v, давления Р и высоты h. Следовательно,

где F1=P1S1 и F2=-P2S2 (отрицательна, так как направлена в сторону, противоположную течению жидкости; рис. 3).

Полные энергии Е1 и Е2 будут складываться из кинетической и потенциальной энергий массы m жидкости:

(4)

(5)

Подставляя (4) и (5) в (2) и приравнивая (2) и (3), получим

(6)

Согласно уравнению неразрывности струи для несжимаемой жидкости (1), объем, занимаемый жидкостью, остается постоянным, т. е.

Разделив выражение (6) на , получим

,

где ρ — плотность жидкости. Но так как сечения выбирались произвольно, то можем записать

=const. (7)

Выражение (7) выведено швейцарским физиком Д. Бернулли (1700—1782; опубликовано в 1738 г.) и называется уравнением Бернулли. Как видно из его вывода, уравнение Бернулли — выражение закона сохранения энергии применительно к установившемуся течению идеальной жидкости. Оно хорошо выполняется и для реальныхжидкостей, внутреннее трение которых не очень велико.

Величина Р в формуле (7) называется статическим давлением (давление жидкости поверхность обтекаемого ею тела), величина — динамическим давлением. Величина представляет собой гидростатическое давление.

Для горизонтальной трубки тока (h1=h2) выражение (7) принимает вид

=const, (8)

— называется полным давлением.

Из уравнения Бернулли (8) для горизонтальной трубки тока и уравнения неразрывности (1) следует, что при течении жидкости по горизонтальной трубе, имеющей различные сечения, скорость жидкости больше в местах сужения, а статическое давление больше в более широких местах, т. е. там, где скорость меньше. Это можно продемонстрировать, установив вдоль трубы ряд манометров (рис. 4).

В соответствии с уравнением Бернулли опыт показывает, что в манометрической трубке В, прикрепленной к узкой части трубы, уровень жидкости ниже, чем в манометрических трубках А и С, прикрепленных к широкой части трубы.

Так как динамическое давление связано со скоростью движения жидкости (газа), то уравнение Бернулли позволяет измерять скорость потока жидкости. Для этого применяется трубка Пито — Прандтля (рис. 5).

Прибор состоит из двух изогнутых под прямым углом трубок, противоположные концы которых присоединены к манометру. I помощью одной из трубок измеряется полное давление (Р0), с помощью другой — статическое (Р). Манометром измеряют разность давлений:

, (9)

где — плотность жидкости в манометре. С другой стороны, согласно уравнению Бернулли, разность полного и статического давлений равна динамическому давлению:

(10)

Из формул (9) и (10) получаем искомую скорость потока жидкости:

Уменьшение статического давления в точках, где скорость потока больше, положено в основу работы водоструйного насоса (рис. 6).

Струя воды подается в трубку, открытую в атмосферу, так что давление на выходе из трубки равно атмосферному. В трубке имеется сужение, по которому вода течет с большей скоростью. В этом месте давление меньше атмосферного. Это давление устанавливается и в откачанном сосуде, который связан с трубкой через разрыв, имеющийся в ее узкой части. Воздух увлекается вытекающей с большой скоростью водой из узкого конца. Таким образом, можно откачивать воздух из сосуда до давления 100 мм рт. ст. (1 мм рт. ст.= 133,32 Па).

Уравнение Бернулли позволяет описать физические явления лежащие в основе работы целого ряда устройств и приборов: карбюратор, пульверизатор (рис. 7) и др.

3. ИСТЕЧЕНИЕ ЖИДКОСТИ ИЗ ОТВЕРСТИЯ. ПРИНЦИП РЕАКТИВНОГО ДВИЖЕНИЯ

Уравнение Бернулли используется для нахождения скорости истечения жидкости через отверстие в стенке или дне сосуда. Рассмотрим цилиндрический сосуд с жидкостью, в боковой стенке которого на некоторой глубине ниже уровня жидкости имеется маленькое отверстие (рис. 8).

Рассмотрим два сечения (на уровне h1 свободной поверхности жидкости в сосуде и на уровне h2 выхода ее из отверстия) и напишем уравнение Бернулли:

Так как давления Р1 и Р2 в жидкости на уровнях первого и второго сечений равны атмосферному, т. е. Р1=Р2 , то уравнение будет иметь вид

.

Из уравнения неразрывности (1) следует, что v1/v2 = S1/S2, где S1 и S2 — площади поперечных сечений сосуда и отверстия. Если S1>>S2, то членом можно пренебречь и

(11)

Это выражение получило название формулы Торричелли (Э. Торричелли (1608 – 1647) – итальянский физик и математик.

Итак, скорость истечения жидкости из отверстия, расположенного на глубине h под открытой поверхностью, совпадает со скоростью, которую приобретает любое тело, падая с высоты h. Следует помнить, что этот результат получен в предположении, что жидкость идеальна. Для реальных жидкостей скорость истечения будет меньше, причем тем сильнее отличается от значения (11), чем больше вязкость жидкости.

Струя жидкости, вытекающая из отверстия в сосуде (рис. 9), уносит с собой за время Δt импульс (— плотность жидкости, S — площадь отверстия, v — скорость истечения струи).

Этот импульс сообщается вытекающей жидкости сосудом. По третьему закону Ньютона сосуд получает, от вытекающей жидкости за время Δt импульс, равный — , т. е. испытывает действие силы

(12)

Эта сила называется реакцией вытекающей струи. Если сосуд поставить на тележку, то под действием силы Fr он придет в движение в направлении, противоположном направлению струи.

Найдем значение силы Fr, воспользовавшись выражением (11) для скорости истечения жидкости из отверстия:

(13)

Если бы, как это может показаться на первый взгляд, сила Fr совпадала по величине с силой гидростатического давления, которое жидкость оказывала бы на пробку, закрывающую отверстие, то Fr была бы равна . На самом деле сила Fr оказывается в 2 раза большей. Это объясняется тем, что возникающее при вытекании струи движение жидкости в сосуде приводит к перераспределению давления, причем давление вблизи стенки, лежащей против отверстия, оказывается несколько большим, чем вблизи стенки, в которой сделано отверстие.

На реакции вытекающей струи газа основано действие реактивных двигателей и ракет. Реактивное движение, не нуждаясь для своего осуществления в наличии атмосферы, используется для полетов в космическом пространстве.

Основоположником теории межпланетных сообщений является выдающийся русский ученый и изобретатель (1857—1935). Он дал теорию полета ракеты и обосновал возможность применения реактивных аппаратов для межпланетных сообщений. В частности, Циолковским была разработана теория движения составных ракет, в которых каждая последующая ступень вступает в действие после того, как предыдущая ступень, израсходовав полностью топливо, отделится от ракеты. Идеи Циолковского получили дальнейшее развитие и были осуществлены учеными и инженерами для освоения космического пространства.

Формула уравнения Бернулли

Определение и формула уравнения Бернулли

При рассмотрении движения жидкости очень часто считают, что перемещение одних частей жидкости относительно других не порождает сил трения. При этом жидкость, у которой вязкость (внутреннее трение) равна нулю, носит название идеальной.

Сжимаемой называют жидкость, плотность которой изменяется и может зависеть от температуры и давления.

Баротропной называют жидкость (или газ), плотность которой валяется функцией давления (не является функцией температуры).

Течение жидкости или газа называют стационарным, если скорость и давление жидкости остаются постоянными в каждой точке жидкости (газа).

Установившееся течение идеальной баротропной жидкости в потенциальном поле сил подчиняется уравнению Бернулли:

где $\varphi_$ – потенциал поля массовых сил; C – величина постоянная для всех точек, которые принадлежат одной линии тока и переменная при переходе к другой линии тока; $\rho$ – плотность идеальной жидкости; p – давление, v – скорость жидкости.

Частные случаи уравнения Бернулли

При воздействии на жидкость только силы тяжести (нет других массовых сил), то потенциал поля можно представить:

где g – ускорение свободного падения, ось OZ имеет направление вверх (z – координата (или высота) по данной оси), тогда уравнение Бернулли можно записать как:

В том случае, если идеальную жидкость можно считать несжимаемой, уравнение Бернулли применяют в виде:

где $\frac<\rho v^<2>><2>$ – называют скоростным напором или динамическим давлением; p – статическое давление в той точке пространства, где расположен центр массы исследуемого элемента жидкости; $\frac><\rho g>$ – носит название пьезометрической высоты; $\frac><2 g>$ – скоростная высота, z – высота на которой находится элемент жидкости, который рассматривается.

Расчеты, которые проводят для реальных жидкостей с применением уравнения Бернулли, дают неплохие результаты.

Следствие уравнения Бернулли

1. Пусть все точки текущей жидкости имеют одинаковые величины скоростей. В таком случае для любых произвольных точек, относящихся к одной линии тока, выполняется равенство:

где p₁ и p₂ – давления в точках жидкости, находящихся на высоте z₁ и z₂, соответственно по вертикальной оси OZ.

Выражение (5) означает, что распределение давления является таким же, как в жидкости, находящейся в покое.

2. Для линии тока, если она горизонтальна уравнение Бернулли (3) примет вид:

что означает: давление оказывается меньше там, где скорость больше.

Примеры решения задач

Задание. Какова скорость течения воды в горизонтальной трубе рис.1? Если в манометрических трубках, указанных на том же рис.1 разность уровней жидкости равна h. Считайте, что диаметры трубок одинаковы.

Решение. В качестве основы для решения задачи используем уравнение Бернулли в виде:

Запишем уравнение Бернулли для трубки тока в месте нахождения манометрических трубок (1) и (2) (используем (1.1)):

Для линии тока при постоянной скорости течения жидкости выполняется:

$$\frac<\rho v^<2>><2>=\rho g\left(h_<2>-h_<1>\right)=\rho g h \rightarrow v=\sqrt<2 g h>$$

Ответ. $v=\sqrt<2 g h>$

Задание. Используя уравнение Бернулли для идеальной несжимаемой жидкости, рассматривая истечение ее из маленького отверстия в широком открытом сосуде, получите формулу Торричелли: $v=\sqrt<2 g h>$, где h=h₂-h₁ — высота открытой поверхности жидкости над отверстием, v – скорость истечения жидкости из отверстия.

Решение. Сделаем рисунок.

Рассмотрим рис.2. Выделим в жидкости трубку тока с сечениями S₁ – площадь открытой поверхности жидкости, S₂ – площадь сечения струи из отверстия. Будем считать, что для всех точек каждого из данных сечений скорость жидкости (v) и высота (h) над избранным начальным уровнем одинаковы. Значит к рассматриваемым сечениям применимо уравнение Бернулли:

где для двух рассматриваемых сечений давления p₁=p₂=p (p — атмосферное давление), скоростью перемещения открытой поверхности можно пренебречь, так как она мала. Уравнение (2.1) двух сечений трубки тока в таком случае упрощается до равенства:

$$\rho g h_<1>=\frac<\rho v^<2>><2>+\rho g h_ <2>\rightarrow \frac><2>=g h_<2>-g h_ <1>\rightarrow v=\sqrt<2 g h>(2.2)$$

здесь v – скорость, с которой вытекает жидкость из отверстия.

Уравнение Бернулли и следствия из него

Выделим в стационарно текущей идеаль­ной жидкости (физическая абстракция, т. е. воображаемая жидкость, в которой от­сутствуют силы внутреннего трения) труб­ку тока, ограниченную сечениями S₁и S₂, по которой слева направо течет жидкость (рис.6.3). Пусть в месте сечения S₁ ско­рость течения v₁, давление р₁и высота, на которой это сечение расположено, h₁. Ана­логично, в месте сечения S₂скорость течения v₂, давление p₂ и высота сечения h₂. За малый промежуток времени Δt жид­кость перемещается от сечений S₁ и S₂ к сечениям S′₁ и S′₂.

Согласно закону сохранения энергии, изменение полной энергии W₂– W₁ идеаль­ной несжимаемой жидкости должно быть равно работе А внешних сил по перемеще­нию массы т жидкости:

С другой стороны, А — это работа, совершаемая при перемещении всей жид­кости, заключенной между сечениями S₁и S₂,за рассматриваемый малый проме­жуток времени Δt. Для перенесения массы т от S₁ до S’₁жидкость должна переме­ститься на расстояние l₁ = υ₁Δt и от S₂ до S’₂— на расстояние l₂ = υ₂Δt. Отметим, что l₁и l₂настолько малы, что всем точкам объемов, закрашенных на рис.6.3, припи­сывают постоянные значения скоро­сти υ, давления р и высоты h. Следова­тельно,

Полные энергии W₁и W₂будут склады­ваться из кинетической и потенциальной энергий массы т жидкости:

Подставляя (6.5) и (6.6) в (6.3) и приравнивая (6.3) и (6.4), получим

Согласно уравнению неразрывности для несжимаемой жидкости (6.2), объем, занимаемый жидкостью, остается посто­янным, т. е.

Разделив выражение (6.5) на ΔV, по­лучим

где ρ — плотность жидкости. Но так как сечения выбирались произвольно, то мо­жем записать

ρυ 2 /2 + ρgh + p = const. (6.8)

Выражение (6.8) называется уравне­нием Бернулли.Как видно из его вывода, уравнение Бернулли — выражение закона сохранения энергии применительно к уста­новившемуся течению идеальной жидко­сти. Оно хорошо выполняется и для реаль­ных жидкостей, внутреннее трение кото­рых не очень велико.

Величина р в формуле (6.8) называ­ется статическим давлением(давление жидкости на поверхность обтекаемого ею тела), величина ρυ 2 /2 — динамическим давлением.Как уже указывалось выше, величина ρgh представляет со­бой гидростатическое давление.

Для горизонтальной трубки тока (h₁= h₂) выражение (6.8) принимает вид

где p + ρυ 2 /2называется полным давле­нием.

Из уравнения Бернулли (6.9) для горизонтальной трубки тока и уравнения неразрывности (6.2) следует, что при течении жидкости по горизонтальной трубе, имеющей различные сечения, скорость жидкости больше в местах сужения, а ста­тическое давление больше в более широ­ких местах, т. е. там, где скорость меньше. Это можно продемонстрировать, устано­вив вдоль трубы ряд манометров(рис.6.4). В соответствии с уравнением Бернулли опыт показывает, что в мано­метрической трубке В, прикрепленной к узкой части трубы, уровень жидкости ниже, чем в манометрических трубках А и С, прикрепленных к широкой части трубы.

Так как динамическое давление связа­но со скоростью движения жидкости (га­за), то уравнение Бернулли позволяет из­мерять скорость потока жидкости. Для этого применяется трубка Пито — Прандтля (рис.6.5). Прибор состоит из двух изогнутых под прямым углом трубок, про­тивоположные концы которых присоедине­ны к манометру. С помощью одной из трубок измеряется полное давление (р₀), с помощью другой — статическое (р). Ма­нометром измеряется разность давлений:

где ρ₀— плотность жидкости в манометре. С другой стороны, согласно уравнению Бернулли, разность полного и статическо­го давлений равна динамическому давле­нию:

Из формул (6.10) и (6.11) получаем иско­мую скорость потока жидкости:

υ = 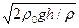. (6.12)

Уменьшение статического давления в точках, где скорость потока больше, положено в основу работы водоструйного насоса(рис.6.6). Струя воды подается в трубку, открытую в атмосферу, так что давление на выходе из трубки равно ат­мосферному. В трубке имеется сужение, по которому вода течет с большей скоро­стью. В этом месте давление меньше ат­мосферного. Это давление устанавливает­ся и в откачанном сосуде, который связан с трубкой через разрыв, имеющийся в ее узкой части. Воздух увлекается вытекаю­щей с большой скоростью водой из узкого конца. Таким образом можно откачивать воздух из сосуда до давления 100 мм.рт.ст.

Уравнение Бернулли используется для нахождения скорости истечения жидкости через отверстие в стенке или дне сосуда. Рассмотрим цилиндрический сосуд с жид­костью, в боковой стенке которого на не­которой глубине ниже уровня жидкости имеется маленькое отверстие (рис.6.7).

Рассмотрим два сечения (на уровне h₁ свободной поверхности жидкости в сосуде на уровне h₂ выхода ее из отверстия). Напишем для них уравнение Бернулли:

Так как давления р₁и р₂в жидкости на уровнях первого и второго сечений равны атмосферному, т. е. p₁ = p_2, то уравнение будет иметь вид
υ₁ 2 /2 + gh₁ = υ₂ 2 /2 + gh₂.

υ₂ = 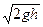. (6.13)

Это выражение получило название форму­лы Торричелли.