Имеет ли уравнение корень на отрезке

Решение тригонометрических уравнений на промежутке

Разделы: Математика

Цель урока:

а) закрепить умения решать простейшие тригонометрические уравнения;

б) научить выбирать корни тригонометрических уравнений из заданного промежутка

Ход урока.

1. Актуализация знаний.

а)Проверка домашнего задания: классу дано опережающее домашнее задание – решить уравнение и найти способ выбора корней из данного промежутка.

1)cos x = -0,5, где хI [- ]. Ответ: .

2) sin x = , где хI [0;2?]. Ответ: ; .

3)cos 2x = —, где хI [0;]. Ответ:

Ученики записывают решение на доске кто-то с помощью графика, кто-то методом подбора.

В это время класс работает устно.

Найдите значение выражения:

а) tg – sin + cos + sin . Ответ: 1.

б) 2arccos 0 + 3 arccos 1. Ответ: ?

в) arcsin + arcsin . Ответ: .

г) 5 arctg (-) – arccos (-). Ответ:– .

– Проверим домашнее задание, откройте свои тетради с домашними работами.

Некоторые из вас нашли решение методом подбора, а некоторые с помощью графика.

2. Вывод о способах решения данных заданий и постановка проблемы, т. е. сообщение темы и цели урока.

– а) С помощью подбора решать сложно, если задан большой промежуток.

– б) Графический способ не даёт точных результатов, требует проверку, и занимает много времени.

– Поэтому должен быть ещё как минимум один способ, наиболее универсальный -попробуем его найти. Итак, чем мы будем заниматься сегодня на уроке? (Учиться выбирать корни тригонометрического уравнения на заданном промежутке.)

– Пример 1. (Ученик выходит к доске)

cos x = -0,5, где хI [- ].

Вопрос: Отчего зависит ответ на данное задание? (От общего решения уравнения. Запишем решение в общем виде). Решение записывается на доске

х = + 2?k, где k R.

– Запишем это решение в виде совокупности:

– Как вы считаете, при какой записи решения удобно выбирать корни на промежутке? (из второй записи). Но это ведь опять способ подбора. Что нам необходимо знать, чтобы получить верный ответ? (Надо знать значения k).

(Составим математическую модель для нахождения k).

1 уровень: № 295 (а,б), № 317 (а,б)

2 уровень: № 307 (в), № 308 (б), № 326(б), № 327(б).

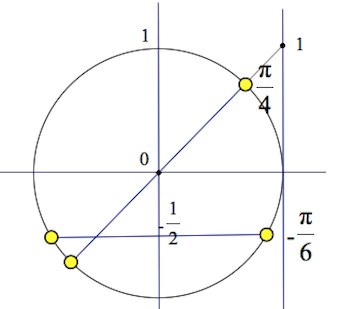
С1 (№15) с отбором корней на отрезке

В рамках подготовки к ЕГЭ по математике рассмотрим задачу С1 ( В новом формате ЕГЭ по математике – «Задание №13» ) , которая предлагалась в Тренировочной работе №60 А. Ларина.

а) Решите уравнение

б) Найдите все корни на промежутке

a)

Применяем формулу двойного угла для :

(1) или (2) ;

Уравнение (2) равносильно уравнению (произвели деление на ).

Откладываем на оси синусов , на оси тангенсов . Выходим на четыре серии точек:

Ответ:

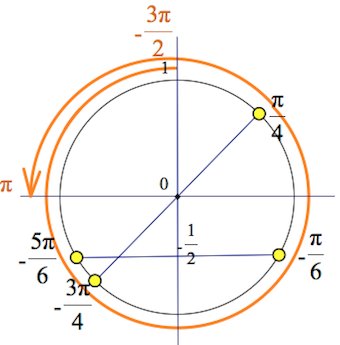
б) Произведем отбор корней из отрезка при помощи тригонометрического круга:

Ответ:

Чтобы не потерять страничку, вы можете сохранить ее у себя:

Можете подробно объяснить, как проводится отбор корней?

Следует хорошо ориентироваться в тригонометрическом круге.
Долго объяснять на словах…
Если никак с кругом, то
решаем сначала неравенство:


Так как , то
При , при .
Потом
И так далее..

Помогите мне! Пn/2 на отрезке [0,1]

При n=0 x=0, 0 входит в [0;1].
При n=1 x=pi\2, pi\2>1.
Только 0.

Объясните по-подробнее какие страницы в какой последовательности надо читать, чтобы научиться отбирать корни тригонометрического уравнения в задании 13 профильного уровня!
А то я в приведённой вами ссылке в сообщении прочитал статью, на ней переход к странице: https://egemaximum.ru/trigonometricheskij-krug-ii/
А после этой страницы не написано куда дальше идти!
Спасибо большое!

Спасибо огромное вам!
Выручаете!=)
А подскажите, чтобы научиться правильно отбирать корни в 13ом задании нужно знать формулы приведения, суммы синусов и т. п?
И отличается ли отбор корней когда один оборот и когда несколько?!
Спасибо!

Для отбора корней не нужны формулы приведения, суммы синусов и т.п.
Принцип отбора – один, не важно полтора оборота, два или один…
Полезно хотя бы раз развернуть тригонометрический круг в ось. И увидеть, что, например, точки на круге отображаются одной точкой, а на оси – разными. Или, например, изобразите точки на круге, затем на оси…

Спасибо!
А при отборе корней с помощью окружности нужно что-то вычислять? Не понимаю когда находят серию корней как они определяют что будет корнем и отмечают это на окружности а что нет?

Не очень понятен вопрос…
Вам следует сперва научиться видеть серии корней на окружности. Только потом осваивайте отбор (при помощи тригонометрической окр.).
Например, если вас просят отметить на окружности точки а вы не понимаете, – как это. то до отбора далеко…
Начинайте перебирать различные значения смотрите, что получается…

Я про то, например, нашли серию корней: x=+_pi/6+pi n, n принадлежит Z.
Просят отобрать (в этапе б) корни на промежутке [2pi;3pi], я нахожу этот помежуток и выделяю его (это очень легко!).
А как вычислить корни, которые попадут на окружность на выделенный промежуток?!
Например, дано уравнение: 16cos^4x-24cos^2x+9=0
Его решить а.
Отобрать корни на промежутке [2pi; 3pi] б.
Нашел серию корней: x=+_pi/6+2pi n, n принадлежит Z.
Далее – черчу окружность, выделяю жирным промежуток, указанный в условии.
Мне не ясно, как туда попали корни 13 pi/6 и 17 pi/6.
Откуда они?
Спасибо огромное за объяснение!

Пока вы не выучите основные углы от нуля до 2пи на тригонометрическом круге, вы не сдвинетесь с места. Я вам много чего сказала по делу, но вы меня не слышите…

Я знаю эти углы! И как их отмечать на окружности! И формулы приведения!
Но я задал вопрос?

Лекция на тему «Метод половинного деления»
план-конспект занятия

Лекция по дисциплине Численные методы для студентов специальности 09.02.07 Информационные системы и программирование

Скачать:

Предварительный просмотр:

«Метод половинного деления решения алгебраических и трансцендентных уравнений»

1. Постановка задачи решения уравнений

Пусть имеется уравнение вида f(x)=0 , (2.1)

где f(x) — алгебраическая или трансцендентная функция.

Решить такое уравнение – значит установить, имеет ли оно корни, сколько корней, и найти значения корней (с указанной точностью).

1. Отделение корней алгебраических и трансцендентных уравнений

Решение указанной задачи начинается с отделения корней, т.е. с установления:

• количества корней;
• наиболее «тесных» промежутков, каждый из которых содержит только один корень.

Чтобы выяснить имеет ли уравнение корень:

1) Строят график функции y=f(x) для уравнения вида f(x)=0. Значения действительных корней уравнения являются абсциссами точек пересечения графиков функций y=f(x) с осью Ох.

y=f(x) кривая трижды пересекает ось абсцисс, следовательно уравнение f(x)=0 имеет три простых корня

если кривая касается оси абсцисс, то уравнение имеет двукратный корень

если кривая имеет точку перегиба, следовательно уравнение имеет трехкратных действительных корень.

2) представляют уравнение в виде f(x)=g(x) и стоят графики функции y=f(x) и y=g(x). Значения действительных корней уравнения являются абсциссами точек пересечения графиков функций у=f(х) и y=g(x). По графику определяются два числа а и b, между которыми заключен корень.

кривые y=f(x) и y=g(x) пересекаются в двух точках, абсциссы которых х 1 и х 2 являются корнями уравнения f(x)=g(x)

При решении задачи об отделении корней бывают полезными следующие очевидные положения:

1. Если непрерывная на отрезке [ a;b ] функция f(x) принимает на его концах значения разных знаков (т.е. f(a) . f(b) ), то уравнение (2.1) имеет на этом отрезке, по меньшей мере, один корень.
2. Если функция f(x) к тому же еще и монотонна, то корень на отрезке [ a;b ] единственный.

Пример: Для графического отделения корней уравнения преобразуем его к равносильному уравнению и отдельно построим графики функций .

Из рисунка видно, что графики пересекаются в одной точке, то есть уравнение имеет единственный корень х= Е и этот корень находится на отрезке [1;1,5].

Вычислим для проверки значения функции на концах отрезка [1;1,5]: f(1)=0.909298; f(1,5)= -0,264344, на концах отрезка значения функции имеют разные знаки, тогда корень на отрезке [1;1,5] действительно имеется.

Для уточнения корней можно пользоваться различными методами. Рассмотрим некоторые из них.

1. Метод половинного деления

Пусть уравнение (2.1) имеет на отрезке [ a;b ] единственный корень, причем функция f(x) на этом отрезке непрерывна.

1) Разделим отрезок [ a;b ] пополам точкой с=(a+b)/2 .

2) Если f(c)=0, то корень найден.

3) Если f(c)≠ 0(что практически наиболее вероятно), то нужно выбрать отрезок, на котором расположен корень. Возможны два случая: f(x) меняет знак либо на отрезке [ a;с ] (рис 2.1), либо на отрезке [ с;b ] (рис 2.2).

Рис 2.1. – функция f(x) меняет знак Рис 2.2. – функция f(x)

на отрезке [a;c] меняет знак на отрезке [c;b]

Выбирая отрезок, на котором функция меняет знак, мы выбираем отрезок, содержащий корень.

4) Этот отрезок снова делим пополам и повторяем шаги 1)-3)

Тогда, либо через конечное число делений отрезка пополам найдём точное значение корня, либо построим бесконечную последовательность вложенных отрезков:
[a; b] [a1; b1] . [an; bn], длины которых стремятся к нулю.

Как только |b n –a n |/2 E , где Е — заданная точность, то в качестве
приближённого значения корня можно взять середину этого отрезка: х=(a n +b n )/2.

Метод половинного деления требует утомительных ручных вычислений, однако он легко реализуется с помощью программы на компьютере.

1. Пример решения уравнений методом половинного деления

Пример: Найти корень уравнения на отрезке [1,3;1,5] с точностью до

Решение: Уравнение имеет единственный корень на отрезке [1,3;1,5].

1. Уточним корень уравнения: Найдем середину отрезка [1,3;1,5]: .

Определим, на каком из полученных отрезков [1,3;1,4] и [1,4;1,5] функция меняет свой знак.

Значит, корень уравнения находится на отрезке [1,3;1,4].

Проверим, достигается ли заданная точность решения 10 -4 :

, точность не достигнута.

1. Продолжаем процесс разделим отрезок [1,3;1,4] пополам точкой .

Определим, на каком из полученных отрезков [1,3;1,35] и [1,35;1,4] функция меняет свой знак.

Значит, корень уравнения находится на отрезке [1,35;1,4].

Проверим, достигается ли заданная точность решения 10 -4 :

, точность не достигнута.

1. Снова разделим отрезок [1,35;1,4] пополам точкой .

Определим, на каком из полученных отрезков [1,35;1,375] и [1,375;1,4] функция меняет свой знак.

Значит, корень уравнения находится на отрезке [1,375;1,4].

Проверим, достигается ли заданная точность решения 10 -4 :

, точность не достигнута.

1. Продолжая делить отрезок пополам и проверять знаки функции на новых промежутках, до тех пор, пока не будет достигнута нужная точность решения ( сделайте самостоятельно ), получим:

Решение уравнения с точностью 10 -4 : х=1,3994.

Алгоритм метода половинного деления

1) Найдем середину отрезка [a; b]: c=(a+b)/2;
2) Вычислим значения функции в точках a и c и найдем произведение полученных значений: d=f(c)*f(a);
3) Если d>0, то теперь точкой a станет c: a=c; Если d ε или

|a-b|/2> ε , то идем в пункт 1) если нет, то корень с нужной нам точностью найден, и он равен: x=(a+b)/2;