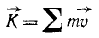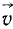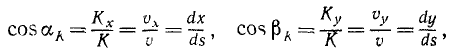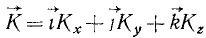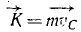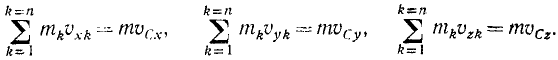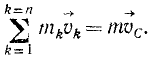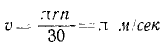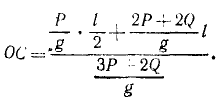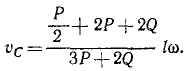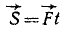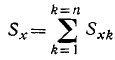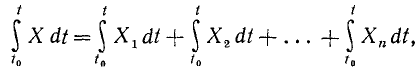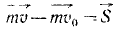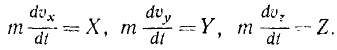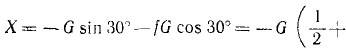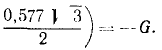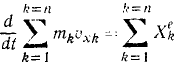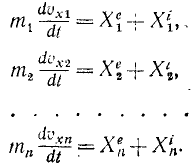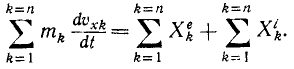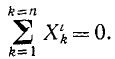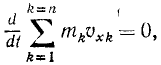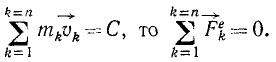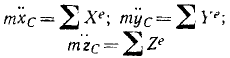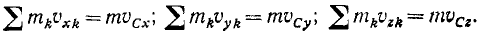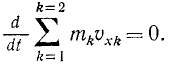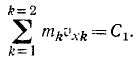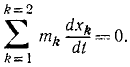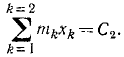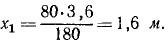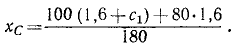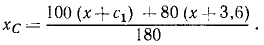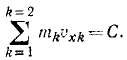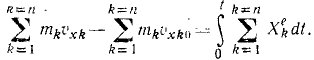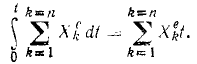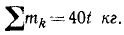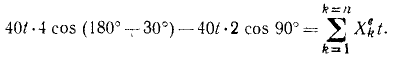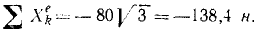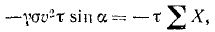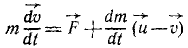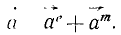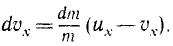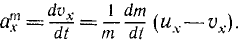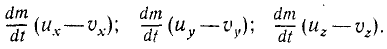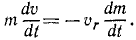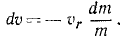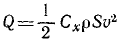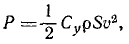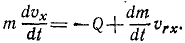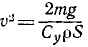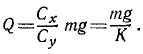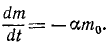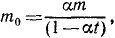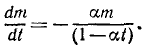Импульс системы материальных точек уравнение движения центра масс

Физический факультатив. Тема: «Импульс, центр масс, движение центра масс»

В работе рассмотрены некоторые задачи на движение центра масс, рассматриваемые на школьном факультативе по физике в Лицее научно-инженерного профиля города Королева. Представляется, что данная статья может быть полезной как для учителей физики школ с углубленным изучением предмета, так и для абитуриентов.

Импульс или количество движения материальной точки есть вектор, равный произведению массы этой точки m на вектор ее скорости v: .

Импульс силы – это вектор, равный произведению силы на время ее действия: . Если сила не является постоянным вектором, то под F следует понимать среднее значение вектора силы за рассматриваемый интервал времени.

Теорема об изменении импульса материальной точки. Пусть на материальную точку m действует постоянная сила F. Тогда

, или . Таким образом изменение импульса материальной точки равно импульсу силы, действующей на нее.

Импульс системы материальных точек равен по определению сумме импульсов всех N точек системы:

Изменение импульса системы материальных точек равно импульсу равнодействующей внешних сил, действующих на систему.

Изолированная (замкнутая) система – это такая система материальных точек, на которую не действуют внешние силы или их равнодействующая равна нулю.

Закон сохранения импульса: импульс изолированной системы материальных точек сохраняется, каково бы ни было взаимодействие между ними:

Если внешние силы, действующие на систему не равны нулю, но существует такое неизменное направление (например, ось OX), что сумма проекций внешних сил на это направление равна нулю, то проекция импульса системы на это направление сохраняется.

Центр масс системы материальных точек. Центром масс N материальных точек m₁, m₂,…, m_N, положения которых заданы радиус-векторами , называют воображаемую точку, радиус-вектор которой определяется формулой:

.

Тогда координаты центра масс равны:

,

,

.

Скоростью центра масс является вектор

,

где – скорость i-й точки.

Ускорением центра масс является вектор

где – ускорение i-й точки.

Теорема об ускорении центра масс системы материальных точек. Произведение суммы масс точек системы на ускорение центра масс равно сумме внешних сил, действующих на точки системы.

Если на систему материальных точек не действуют внешние силы, то скорость центра масс относительно любой инерциальной системы отсчета сохраняется, каково бы ни было взаимодействие внутри системы.

Если при этом скорость центра масс относительно некоторой инерциальной системы была равна нулю, то сохраняется и положение центра масс.

Два этих утверждения являются прямыми следствиями закона сохранения импульса.

Задача 1. Частица массы m движется со скоростью v, а частица массы 2m движется со скоростью 2v в направлении, перпендикулярном направлению движения первой частицы. На каждую частицу начинают действовать одинаковые силы. После прекращения действия сил первая частица движется со скоростью 2v направлении, обратном первоначальному. Определите скорость второй частицы. [1]

Изменение импульса частицы массой m вследствие действия импульса силы равно 3mv, следовательно вторая частица приобретает точно такой же импульс перпендикулярно направлению ее движения. Полный импульс второй частицы находится векторным сложением его составляющих по двум перпендикулярным направлениям и равен 5mv. Скорость второй частицы тогда равна 5v/2.

Задача 2. Ящик с песком массы М лежит на горизонтальной плоскости, коэффициент трения с которой равен µ. Под углом ? к вертикали в ящик со скоростью v влетает пуля массы m и почти мгновенно застревает в песке. Через какое время после попадания пули в ящик, начав двигаться, остановится? При каком значении ? он вообще не сдвинется? [1]

Решение. Изменение импульса системы материальных точек равно импульсу равнодействующей внешних сил, действующих на систему. По горизонтальной и вертикальной оси:

где u – скорость ящика сразу после того, как пуля в нем застрянет, N – реакция опоры, – время, за которое пуля застревает в песке. Из этих уравнений следует

Так как пуля застревает почти мгновенно последним членом в правой части можно пренебречь. После того, как пуля застрянет, ящик тормозит под действие силы трения с ускорением . Ящик останавливается за время . Ящик не сдвинется, если .

Задача 3. По наклонной плоскости, составляющей угол а с горизонтом, с постоянной скоростью v съезжает ящик с песком массой M. В него попадает летящая горизонтально пуля массой m, и ящик при этом останавливается. С какой скоростью u летела пуля?

Решение. Вдоль наклонной плоскости изменение импульса системы

Поперек наклонной плоскости

Тогда

и с учетом того, что (ящик съезжает с постоянной скоростью)

Задача 4. Обезьяна массы m уравновешена противовесом на блоке А. Блок А уравновешен грузом массы 2m на блоке В. Система неподвижна. Как будет двигаться груз, если обезьяна начнет равномерно выбирать веревку со скоростью u относительно себя? Массой блоков и трением пренебречь. [1]

Решение. Обезьяна получает импульс силы и начинает двигаться со скоростью v к потолку. Точно такой же импульс силы получает груз m и тоже движется со скоростью v к потолку. Груз массой 2m получает импульс силы и тоже движется со скоростью v к потолку. Блок А опускается вниз со скоростью v. груз m движется относительно блока А вверх со скоростью 2v. Веревка справа от блока А движется от потолка со скоростью 3v. относительно обезьяны веревка движется вниз со скоростью 4v. Отсюда .

Задача 5. Из однородной круглой пластины радиусом R вырезали круг вдвое меньшего радиуса, касающийся края пластины. Найти центр тяжести полученной пластины.

Решение. Пусть масса пластины до вырезания равна M. Тогда масса вырезанной части равна M/4. Предположим, что имеется в наличии вещество с отрицательной массой, Тогда вырез можно получить наложением на пластину пластинки с отрицательной массой —M/4. Тогда, поместив начало координат в центр круга и направив ось X направо, положение центра масс получаем из формулы для координаты центра масс:

.

Задача 6. На гладком полу стоит сосуд, заполненный водой плотности p₀; объем воды V₀. Оказавшийся на дне сосуда жук объема V и плотности p через некоторое время начинает ползти по дну сосуда со скоростью u относительно него. С какой скоростью станет двигаться сосуд по полу? Массой сосуда пренебречь, уровень воды все время остается горизонтальным. [1]

Решение. Пусть скорость сосуда v, тогда скорость жука относительно пола u+v. Импульс системы по горизонтальной оси сохраняется и равен нулю. Удобно рассматривать жука как совокупность воды массой и сублимированного вещества жука массой , которое перемещается относительно всей воды. Тогда импульс системы

и

Задача 7. На дне маленькой запаянной пробирки, подвешенной над столом на нити, сидит муха, масса которой равна массе пробирки, а расстояние от поверхности стола равно длине пробирки l. Нить пережигают, и за время падения пробирки муха перелетает со дна в верхний конец пробирки. Определить время, за которое пробирка достигнет стола.

Решение. Ускорение центра масс системы определяется силами тяжести, действующими на пробирку и муху, и равно g. За время падения центр масс системы переместился на l/2. Отсюда время падения .

Задача 8. На нити, перекинутой через блок, подвешены два груза неравной массы (m₂ > m₁). Определить ускорение центра масс этой системы. Массой блока и нити пренебречь. [2]

Решение. Ускорение тяжелого груза направлено вниз и, как известно, равно . Ускорение легкого груза такое же по модулю, но направлено вверх. Ускорение центра масс находим по формуле из теоретического раздела

Задача 9. В сосуде, наполненном водой плотности p, с ускорением а всплывает пузырек воздуха, объем которого V. Найдите силу давления со стороны сосуда на опору. Масса сосуда вместе с водой равна m. [1]

Решение. Будем рассматривать системы как совокупность сосуда с водой массой и шарика с отрицательной массой , который поднимается вверх с ускорением a. Тогда ускорение центра масс системы

и направлено вниз. Из теоремы об ускорении центра масс

, и отсюда сила давления на опору, численно равная реакции опоры N,

Задачи для самостоятельного решения.

Задача 10. С горы с уклоном a () съезжают с постоянной скоростью сани с седоком общей массой M. Навстречу саням бежит и запрыгивает в них собака массой m, имеющая при прыжке в момент отрыва от поверхности горы скорость v, направленную под углом () к горизонту. В результате этого сани продолжают двигаться по горе вниз со скоростью u. Найти скорость саней до прыжка собаки. (Билет 3, 1991, МФТИ) [3]

Ответ:

Задача 11. Человек, находящийся в лодке, переходит с носа на корму. На какое расстояние S переместится лодка длиной L, если масса человека m, а масса лодки M? Сопротивлением воды пренебречь.

Ответ:

Задача 12. На поверхности воды находится в покое лодка. Человек, находящийся в ней, переходит с кормы на нос. Как будет двигаться лодка, если сила сопротивления движению пропорциональна скорости лодки?

Ответ: Лодка сместится, а затем вернется в исходное положение.

Задача 13. На первоначально неподвижной тележке установлены два вертикальных цилиндрических сосуда, соединенных тонкой трубкой. Площадь сечения каждого сосуда S, расстояние между их осями l. Один из сосудов заполнен жидкостью плотности p. Кран на соединительной трубке открывают. Найдите скорость тележки в момент времени, когда скорость уровней жидкости равна v. Полная масса всей системы m. [1]

Ответ:

Задача 14. На тележке установлен цилиндрический сосуд с площадью сечения S, наполненный жидкостью плотности p. От сосуда параллельно полу отходит длинная и тонкая горизонтальная трубка, небольшой отрезок которой вблизи конца загнут по вертикали вниз. Расстояние от оси сосуда до отверстия трубки равно L. Уровень жидкости в сосуде опускается с ускорением а. Какой горизонтальной силой можно удержать тележку на месте? [1]

Ответ:

Литература.

1. Задачи по физике: Учеб. пособие/ И.И. Воробьев, П.И. Зубков, Г.А. Кутузова и др.; Под ред. О.Я. Савченко. ? 2-е изд., перераб. М.: Наука. Гл. ред. физ.-мат. лит. 1988. — 416 с.

2. Дмитриев С.Н., Васюков В.И., Струков Ю.А. Физика: Сборник задач для поступающих в вузы. Изд. 7-е, доп. М: Ориентир. 2005. – 312 с.

3. Методическое пособие для поступающих в вузы / Под. ред. Чешева Ю.В. М.: Физматкнига, 2006. – 288 с.

Количество движения в теоретической механике

Содержание:

Количество движения материальной точки и системы импульс силы:

Количеством движения называют меру механического движения, выражающуюся геометрической суммой произведений массы каждой частицы материальной системы на ее скорость.

Количество движения точки и системы. Ньютон во введении к «Началам» дал такое определение «Количество движения есть мера такового, устанавливаемая пропорционально скорости и массе»

Всякая материальная частица обладает двумя мерами механического движения, о чем уже было сказано в § 37 Одна из этих мер, называемая количеством движения, имеет применение всякий раз, когда
механическое движение от одного тела переходит другому в виде механического же движения Так, например, один биллиардный шар, ударивши другой, передает ему часть своего механического движения, выражаемого количеством движения

Количество движения материальной частицы обладающей массой m и скоростью

(156)

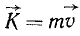
Размерность количества движения в физической системе единиц

например м кг/сек Эта величина принята за единицу количества движения в СИ

В технической системе единиц размерность количества движения

[К]_T = L 0 F 1 T 1 ,

например кГ сек, если в технической системе сила выражена в килограммах, а время — в секундах

Наряду с вектором количества движения в механике применяют проекции количества движения на оси

Направляющие косинусы количества движения равны направляю щим косинусам (62) скорости, так как вектор количества движения материальной точки ичи частицы направлен по скорости.

(62 // )

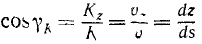
Модуль количества движения легко подсчитать по формуле

(158)

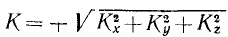
Проекция количества движения на ось (как и проекция на ось всякого вектора)—скаляр 2-го рода и определяется величиной и знаком

Если мы умножим проекцию количества движения на единичный вектор этой оси, то получим составляющую, или компоненту, количества движения по оси Вектор количества движения точки (или материальной частицы) связан со своими компонентами по координатным осям обычным соотношением

Количество движения материальной системы выражается суммой количеств движения всех частиц этой системы «Количество движения целого есть сумма количеств движения отдельных частей его» (Ньютон) Таким образом, для материальной системы, содержащей n частиц или n точек,

(159)

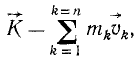
где суммирование распространено на все частицы материальной системы

Под проекцией количества движения системы на какую-либо ось понимают алгебраическую сумму проекции количеств движения всех точек системы на эту ось

(159 / )

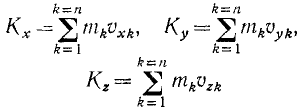
Точку, определяемую координатами, равными отношению статического момента тела или системы относительно соответствующей оси к ею массе, называют центром масс

Центр масс

Ознакомимся с очень важным в динамике понятием, частично известным нам из курса статики твердого тела (см гл VII) Напомним, что центр тяжести твердого тела — это центр параллельных сил, представляющих веса материальных частиц твердого тела Для определения координат центра тяжести мы вывели формулы

(45)

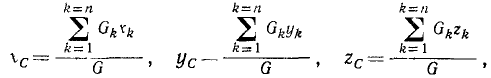
где в числителе — статический момент веса относительно соответствующей оси, а в знаменателе — вес всего тела или в векторной форме

(45 / )

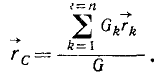
Понятие «центр тяжести» и формулы, определяющие координаты этой точки, связаны с весом, с тяжестью. Но в динамике встречается такое состояние механических систем, при котором подобное определение недостаточно. Вспомним, например, «состояние невесомости», о котором рассказывали наши космонавты,— здесь понятие «вес» и «тяжесть» теряют свой смысл. Кроме того, в мировом пространстве существуют области, где в состоянии невесомости пребывает всякое тело независимо от его движения, как, например, точка пространства, в которой материальное тело притягивается к Земле и к Солнцу с равными и противоположно направленными силами. В таких случаях понятие «центр тяжести тела» теряет смысл, но сама точка продолжает существовать и не теряет своего значения. Поэтому целесообразно определить эту точку в зависимости не от веса, а от массы частиц.

Пусть какое-либо твердое тело или материальная система подвержены действию силы тяжести, и координаты центра тяжести определяются равенствами (45). Поделим в,этих равенствах и числители и знаменатели на ускорение свободно падающего тела. Координаты точки от деления числителя и знаменателя на одно и то же число не изменятся, но в знаменателе мы получим, согласно (124), не вес, а массу системы, а в числителе—статические моменты масс:

(160)

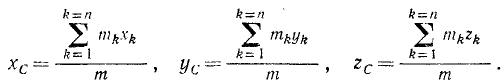
Точка, определяемая координатами (160), совпадает с центром тяжести, но определение ее связано не с весом, а с массой частиц твердого тела или системы. Ее называют центром инерции, или центром масс. Это понятие шире понятия центра тяжести, так как масса не исчезает даже при таких обстоятельствах, при которых вес неощутим.

Количество движения системы материальных точек равно количеству движения ее центра масс, в котором предполагают сосредоточенной массу всей системы:

Выражение количества движения системы через ее массу и скорость центра масс. Координаты центра инерции C материальной системы, движущейся относительно осей xOyz, принимаемых за неподвижные, определяются равенствами (160), где .va, y_k и z_k— переменные координаты точек системы. Из этих равенств, освободившись от знаменателя, определим статические моменты массы на данное мгновение:

(161)

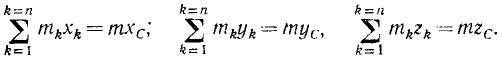
Продифференцировав по времени, находим, что проекция количества движения на ось равна произведению массы системы и проекции скорости центра масс на ту же ось:

Но если равны проекции векторов на любую ось, то, следовательно, равны и сами векторы:

Мы нашли, что количество движения всякой материальной системы равно количеству движения ее центра масс, если сосредоточить в нем массу всей системы:

(162)

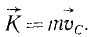
Задача №1

Вычислить количество движения К однородного диска радиуса r =50 см и массы 80 кг в двух случаях:
1) диск вращается вокруг неподвижной оси, проходящей через ею центр, делая 60 об/мин;
2) диск катится без скольжения и буксования по прямолинейному рельсу, делая 60 об/мин.

Решение. Количество движения диска равно количеству движения точки, масса которой равна массе диска, а скорость равна скорости центра масс диска. Задачу решаем в единицах СИ.
1) В первом случае скорость центра масс равна нулю, следовательно, K=O.
2) Во втором случае скорость центра масс определим как вращательную относительно мгновенного центра скоростей, находящегося в точке касания диска и рельса:

K = 80π =251,20 кг . м/сек.

Ответ. 1) К= 0; 2) К = 251,20 кг . м/сек.

Задача №2

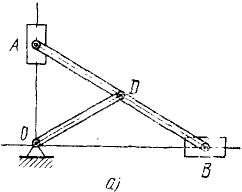
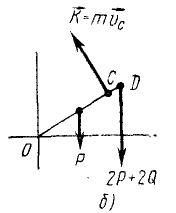
Определить количество движения эллипсографа (рис. 173, а), состоящего из кривошипа OD, линейки А В и двух ползунов, центры масс которых совпадают с шарнирами А и В, соединяющими ползуны с линейкой АВ. Кривошип и линейку рассматривать как однородные стержни веса P и 2Р, причем OD- AD = BD-l, веса ползунов одинаковы и равны Q; кривошип вращается с угловой скоростью ω.

Решение. Механическая система состоит из четырех тел: кривошипа, линейки и двух ползунов. Найдем центр масс системы. Центр масс кривошипа находится в середине кривошипа (рнс. 173, б). Центр масс линейки и двух ползунов совпадает с их центром симметрии D. Центр масс всего механизма лежит на кривошипе между этими точками. Расстояние центра масс системы от точки О определим по (160):

Умножая это расстояние иа угловую скорость ω кривошипа, найдем скорость центра масс системы:

Умножая υ_c на массу 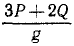всей системы, найдем количество движения системы.

Ответ. Количество движения—вектор, равный 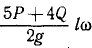, перпендикулярный кривошипу и приложенный в центре масс эллипсографа.

Импульсом постоянной силы называют меру механического воздействия на материальную частицу со стороны других материальных объектов за данный промежуток времени, выражающуюся произведением силы на время ее действия:

Импульс постоянной силы. Мы определили механическое действие материальных тел на данную материальную частицу тремя основными характеристиками: величиной, направлением и продолжительностью. Рассматривая это механическое действие лишь за одно мгновение, мы пришли тогда к понятию силы. Но действие всегда происходит во времени, хотя бывают механические действия (не которые случаи удара), продолжительность которых измеряется всего лишь миллионными долями секунды. 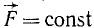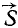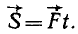Если , то векторную величину , направленную по силе и равную по модулю произведению модуля силы на время ее действия, называют импульсом постоянной силы за данный промежуток времени:

(163)

Определим размерность импульса силы в физической системе единиц:

[S]φ = L 1 M 1 T -1

Единицей импульса силы в системе СИ является 1 м . кг/сек. Размерность импульса силы в технической системе единиц

[S]_r = L 0 F 1 T 1 .

Если сила выражена в кГ, а время — в сек, то единицей импульса силы является 1 кГ . сек.

Размерности импульса силы и количества движения одинаковы.

Импульс переменной силы

Если сила непостоянна по величине или по направлению, то для определения ее импульса за данный промежуток времени надо разбить этот промежуток времени на столь малые интервалы, в течение которых можно пренебречь изменением силы, и определить для каждого такого интервала элементарный импульс. Элементарным импульсом силы называют импульс за столь малый промежуток времени, при котором можно пренебречь изменением силы:
(164)

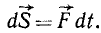
Импульс переменной силы за конечный промежуток времени выражают пределом геометрической суммы элементарных импульсов за бесконечно малые части данного промежутка:

(164 / )

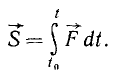
Следовательно, импульс переменной силы за данное время выражается интегралом от вектора 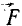по скалярному аргументу t.

Для вычисления импульса переменной силы пользуются его проекциями на оси координат. Построим прямоугольную систему координат и спроецируем элементарный импульс на ось Ох:

Интегрируя в пределах от t₀ до t, находим S_x и аналогично S_y и S_z:

(165)

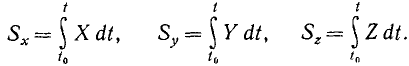
По проекциям (165) легко определить модуль и направляющие косинусы вектора, однако в этом редко встречается необходимость и практически обычно ограничиваются определением проекций (165).

Проекция импульса равнодействующей на любую ось равна сумме проекций импульсов составляющих сил на ту же ось:

Пусть на точку действует несколько сил, проекции которых на какую-либо ось Ox обозначим X1, X2, . Х„, а проекцию ‘ равнодействующей этих сил обозначим X. Тогда

Умножим обе части этого равенства на бесконечно малый промежуток времени dt и проинтегрируем в пределах от t₀ до t:

Итак, проекция импульса равнодействующей на любую ось за данный промежуток времени равна алгебраической сумме проекций импульсов составляющих сил на ту же ось и за то же время, следовательно, импульс равнодействующей равен геометрической сумме импульсов составляющих:
(166 / )

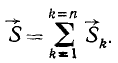
Теоремы о количестве движения точки и системы и о движении центра масс

Изменение количества движения материальной точки за какой-либо промежуток времени равно импульсу силы, действующей на точку за тот же промежуток времени:

Теорема об изменении количества движения материальной точки. По основному закону динамики под действием силы материальная точка получает ускорение. Но, чтобы сообщить материальной точке скорость, сила должна действовать в течение некоторого времени. Таким образом, скорость .материальной точке сообщает не сила, а импульс силы. Конечно, эта скорость зависит не только от импульса силы, но и от массы точки.

Напишем дифференциальные уравнения движения материальной точки в форме (127):

Умножая каждое из уравнений (127) на dt и вводя постоянную m под знак дифференциала, получим

dm υ_x = X dt, dm υ_y = Ydt, dm υ_z = Zdt. (167)

Мы нашли, что дифференциал проекции количества движения равен проекции элементарного импульса силы на ту же ось.

Проинтегрируем левую и правую части первого из этих уравнений в соответствующих пределах υ_0x, υ_x и t₀, t; аналогично поступив и с двумя другими уравнениями, получим:.

(168)

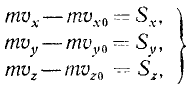
т. е. изменение проекции количества движения материальной точки на ось равно проекции импульса силы на ту же ось и за то же время. Но если равны проекции на любую ось двух векторов, то, следовательно, равны и эти векторы:

(168 / )

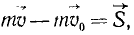
т. е. вектор изменения количества движения материальной точки за какое-либо время равен вектору импульса силы, действующей на материальную точку за то же время. Конечно, и здесь под силой надо понимать равнодействующую, если на точку действует не одна, а несколько сил.

Задача №3

Тяжелая точка массой m кг, получив начальную скорость υ₀ = 24,5 м/сек, поднимается по негладкой плоскости (рис. 174), наклоненной к плоскости горизонта под углом 30°. Сколько времени будет подниматься точка, если коэффициент трения f = 0,577?

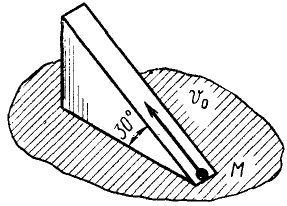
Рис. 174

Решение. Пo заданным силам надо определить время движения точки. Но для решения задачи нет необходимости составлять и интегрировать дифференциальные уравнения движения, а можно воспользоваться теоремой об изменении количества движения. На точку действуют вес G, сила трения F_гр =fG cos 30 o и реакция R плоскости. Направим ось Ox по наклонной плоскости вверх. Проекция равнодействующей всех сил на эту ось равна

Если точка двигалась в течение t сек, то проекция импульса силы за это время равна -Gt. Подставляя в уравнение (168) найденное значение S_x, заданное значение υ_x0 и υ_x = 0, получим —m 24,5 = —Gt, откуда находим t.
Ответ. t — 2,5 сек.

Задача №4

Материальная точка, масса которой m = 3 кг, двигалась по горизонтальной прямой налево со скоростью 5 м/сек. К ней приложили постоянную силу, направленную вправо. Действие силы прекратилось через 30 сек, и тогда скорость точки оказалась равной 45 м/сек и направленной вправо. Найти величину этой силы.

Решение. Условие задачи дано в физической системе единиц (СИ). По изменению скорости точки надо определить силу, производящую данное движение точки. Таким образом, задача является прямой задачей динамики. Решать ее мы будем, применив теорему об изменении количества движения. Примем горизонтальную прямую, по которой движется точка, за ось Ох, считая направление вправо положительным. Тогда

Подставляя эти данные в (168), найдем
— F∙30 = + 3∙45 + 3∙5 -+150 кг . м/сек,

откуда определим силу.
Ответ. F = 5 кг∙м сек 2 = 5 н.

Производная по времени от суммы проекций количеств движения всех материальных точек системы на какую-либо ось равна сумме проекций всех внешних сил системы на ту же ось:

Теорема о проекциях количеств движения системы. Теорема о количестве движения находит большое применение при исследовании движения системы материальных точек, так как в этой теореме исключены все внутренние силы системы.

Пусть дана механическая система, состоящая из n материальных точек. Распределив все силы, приложенные к точкам этой системы, на две категории (силы внешние и силы внутренние), напишем дифференциальные уравнения движения точек системы в форме (129) в проекциях на ось абсцисс:

Сложив отдельно левые и отдельно правые части написанных уравнений, получим

Но сумма проекций всех внутренних сил системы равна нулю, так как внутренние силы, согласно закону равенства действия и противодействия, попарно равны и противоположно направлены:

В левой части постоянные m_k внесем под знак производной, заменим сумму производных производной от суммы и получим для проекций на, ось абсцисс

(169)

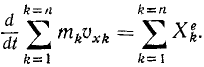
Мы не накладывали никаких ограничений на направление оси абсцисс, поэтому мы можем сформулировать следующую общую теорему, называемую теоремой о проекциях количеств движения системы материальных точек: производная по времени от суммы проекций количеств движения всех точек системы на какую-либо ось равна сумме проекций всех внешних сил системы на тy же ось.

Равенства (169) справедливы для любой оси; следовательно, их можно записать в векторной форме:

(169 / )

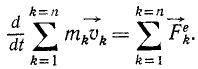
Умножая уравнения (169) на dt и интегрируя, найдем, что изменение суммы проекций количеств движения всех точек системы на какую-либо неподвижную ось за некоторый промежуток времени равно сумме проекций импульсов всех внешних сил системы на ту же ось за то же время:

(170)

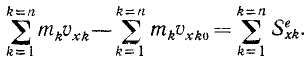
При решении задач это уравнение иногда находит применение, но теорему о проекции количеств движения системы чаще применяют в дифференциальном виде (169), чем в конечном виде (170).

Если сумма проекций всех внешних сил системы на какую-либо ось равна нулю, то сумма проекций количеств движения точек системы на эту ось постоянна

Интеграл количеств движения. В частном случае, если сумма проекций всех внешних сил системы на какую-либо ось, например на ось Ох, равна нулю, то уравнение (169) принимает вид

откуда, проинтегрировав, получаем
(171)

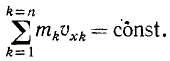
Это равенство называют интегралом количества движения системы материальных точек и словами его можно сформулировать так: если сумма проекций всех внешних сил системы на какую-либо ось равна нулю, то сумма проекций количеств движения всех точек системы на эту ось постоянна.

Справедливо и обратное заключение: если сумма проекций количеств движения системы на какую-либо ось постоянна, то сумма проекций всех внешних сил системы на эту ось равна нулю. В самом деле, дифференцируя (171) по времени, найдем, что производная по времени от суммы проекций количеств движения на ось Ox равна нулю и ввиду (169) равна нулю сумма проекций на эту ось всех внешних сил системы.

Если равна нулю сумма проекций всех внешних сил не только на ось О_х, но также и на оси O_y и O_z, то сохраняется не только сумма проекций на оси, но и геометрическая сумма векторов количеств движения точек системы, т. е.
если 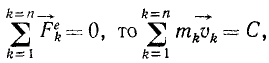(171 / )

если

Такой случай мы можем представить себе в изолированной материальной системе, т. е. в системе, на точки которой не действуют никакие внешние силы. Примером почти полностью изолированной механической системы может служить солнечная система (см. § 36). Количество движения изолированной системы остается неизменным; этот закон называют иногда принципом сохранения количества движения.

Центр масс системы движется как материальная точка, в которой сосредоточена масса всей системы и к которой приложены все внешние силы:

Теорема о движении центра масс

К теореме о проекциях количеств движения примыкает теорема о движении центра масс. Во многих задачах эти теоремы вполне заменяют друг друга. Уже было показано, что сумму количеств движения всех материальных точек системы можно представить как количество движения одной точки, совпадающей с центром инерции системы, обладающей скоростью центра инерции и массой, равной сумме масс всех точек системы:

Дифференцируя эти равенства по времени и принимая во внимание теорему (169) о проекциях количеств движения на O_x, O_y и O_z, найдем:

(172)

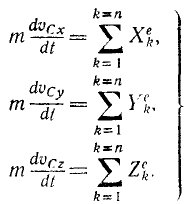
Сравнивая эти уравнения с уравнениями (127), можно убедиться, что движение центра масс математически описывается тремя дифференциальными уравнениями, как и движение материальной точки.

Однако с физической стороны имеется некоторое различие между уравнениями (127) и (172). Всякая материальная точка обладает некоторой массой и движется согласно (127) под действием всех приложенных к ней сил. Центр масс является геометрической точкой и может не совпадать ни с одной из материальных частиц системы.

Уравнения (172) говорят о том, что центр масс (инерции, тяжести) движется как материальная точка, которая имеет массу, равную массе всей системы и к которой приложены силы, равные веем внешним силам, действующим на материальные точки данной системы; внутренние силы не изменяют движения центра масс и не могут нарушить его покоя.

Три уравнения (172) движения центра масс в прямоугольной системе координат могут быть заменены одним векторным уравнением

(172 / )

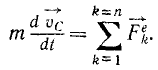
О независимости движения центра масс от внутренних сил. Независимость движения центра масс от действия внутренних сил была установлена Ньютоном. «Центр тяжести системы двух или нескольких тел от взаимодействия тел друг на друга не изменяет ни своего состояния покоя, ни движения», — писал он в «Началах». Теорема о движении центра тяжести (масс) имеет в механике большое значение, а потому необходимо пояснить физическую сущность этой теоремы.

На первый взгляд может показаться, что движение центра масс системы иногда происходит под действием ее внутренних сил. Например, чтобы увеличить скорость парохода, поднимают давление пара, т. е. увеличивают внутренние силы системы. Молодой и здоровый человек с хорошо развитой мускулатурой ног легко обгонит старика с дряблыми мышцами и т. д. и т. п. Но отсюда не следует делать вывод, что центр масс системы передвигается внутренними силами этой системы. В приведенных примерах внутренние силы лишь заставляют точки данной системы воздействовать на окружающие материальные тела, отчего возникают внешние силы, создающие движение центра масс данной системы. Так, человек силой своих мышц (внутренней силой) отталкивается ногами от дороги, отчего в точках соприкосновения подошв с дорогой возникает сила трения (внешняя для человека), направленная в сторону его движения и позволяющая передвигаться всей системе (человеку). Конечно, эта сила зависит от внутренних сил человека, но она является внешней силой, и человек не смог бы идти по поверхности без трения. Ни один силач не может силой своих мышц поднять себя за волосы над Землей. Пароход развивает пары, чтобы быстрее вращать гребной винт и лучше отталкиваться нм от воды. Давление воды на гребной винт является внешней силой для парохода. Никакое давление пара (внутренняя сила) не создало бы движение парохода, если бы не было гребного винта или воды, взаимодействие которых создает силу тяги, являющуюся внешней силой для парохода.

Теоремы о движении центра масс и о количестве движения системы являются основой для расчетов реактивных движений. Ракета для своего полета не нуждается во внешней среде. Газообразные продукты горения с большой скоростью выбрасываются из сопла. Это движение продуктов горения (назовем их пороховыми газами) происходит под действием внутренних сил, а потому не может повлиять па движение центра тяжести всей системы, включающей пороховые газы и корпус ракеты. Если до взрыва ракета была неподвижна, то движение газов так компенсируется движением корпуса ракеты в противоположном направлении, что сумма количеств движения всей системы равна нулю и центр масс всей системы остается неподвижным и после взрыва.

Задача №5

Лодка стоит в неподвижной воде перпендикулярно к берегу, причем расстояние от берега до носа лодки равно 1,6 м, а до кормы 5,2 м. Чтобы пододвинуть лодку к берегу, человек, стоящий на носу лодки, переходит на корму. На каком расстоянии будет нос лодки от берега после перемещения человека, если вес лодки G₁ = 100 кГ, нес человека G₂= 80 кГ, а сопротивлением воды пренебрегаем?

Решение. Физическая сущность задачи состоит в том, что человек переходит с носа на корму, отчего лодка перемещается в обратном направлении. Перемещение человека на лодке, его вес и вес лодки заданы, требуется определить расстояние, на которое переместится лодка вследствие перемещения человека. Здесь механическое движение человека перелается лодке в качестве механического же движения. В подобных задачах обычно применяют теорему о проекциях количеств движения или аналогичную ей теорему о движении центра масс. Мы покажем применение обеих этих теорем.

При решении почти каждой задачи бывает необходимо уточнить два вопроса: 1) движение какой точки, твердого тела или механической системы надо изучить и 2) какие силы действуют на эту точку, это тело или эту систему. Также необходимо выбрать основные единицы измерения, например единицы СИ, тогда масса лодки m₁ = 100 кг, масса человека m₂ = 80 кг.

В данной задаче нужно изучить движение механической системы, состоящей из лодки, представляемой се центром инерции, и человека, принимаемого за материальную точку. На точки этой механической системы действуют различные внешние силы (вес лодки, вес человека, архимедова подъемная сила), но все они вертикальны, а нас интересует горизонтальное перемещение лодки, а потому и горизонтальные силы. В системе действуют внутренние силы (сила, с которой человек отталкивается от стланей, идя по лодке, реакция лодки и др.), но внутренние силы не входят в уравнения (169), (172) и несущественны для данной задачи.

Рис. 175

1-й способ. Применим сначала теорему о проекциях количеств движения системы (169). Построим неподвижную систему координат (рис. 175,а), взяв начало в точке О на берегу и направив ось Ox горизонтально вдоль лодки. Сумма проекций всех внешних сил на Ox равна нулю. Система состоит из двух материальных точек — лодки и человека. Равенство (169) принимает вид

Если сумма проекций внешних снл равна нулю, то имеет место интеграл количеств движения (171). Действительно, проинтегрировав, получаем

Постоянную интеграции C₁ определим из начальных данных: в начальное мгновение лодка и человек были неподвижны. Таким образом, в начальное мгновение количества движения точек системы и сумма количеств движения равнялись нулю, а потому C₁ = 0, т. е.

Умножая на dt и интегрируя, получим

В левой части хк означают перемещения точек системы по оси Ох.
В начальное мгновение этих перемещений не было, а потому, определяя C₂ из начальных данных, находим, что C₂ = O. Раскроем знак суммы, дав индексу k значения 1 и 2 соответственно числу точек системы:

т. е. сумма произведений масс точек системы на их перемещения по оси Ox равна нулю. Здесь под перемещением По оси Ox мы понимаем проекцию абсолютного перемещения точки на Ох. Предположим, что лодка переместилась влево на величину—х₁ (рис. 175, б). Человек в относительном движении передвинулся вправо на длину лодки (3,6 м), но в то же время лодка перенесла его в своем движении влево, следовательно, х₂ = 3,6—x₁. Подставляя эти данные и величины масс в предыдущее уравнение, находим
— 100x₁ + 80 (3,6—x₁) = 0.

У студента, не имеющего достаточного навыка в решении задач, может возникнуть сомнение в правильности знака второго члена. Для проверки знака существует удобное правило: во все члены уравнения х₁ должно входить с одним и тем же знаком, если конечно, эти члены находятся по одну сторону от знака равенства. В данном уравнении все члены находятся слева; первый член —100x₁, следовательно, второй член должен быть +80 (3,6— x₁), так как знак при х₁ должен и во втором члене быть таким же, как и в первом члене.

Решая это уравнение, находим перемещение лодки:

2-й способ. Решим ту же задачу, применив теорему о движении центра масс. До начала движения центр масс всей системы был неподвижен —человек пошел вдоль лодки. Сила взаимодействия между человеком и лодкой является внутренней силой системы «лодка с человеком», а потому не может переместить центр масс этой системы. Для решения задачи надо написать выражения абсциссы Xq центра масс системы при двух положениях системы: 1) человек на носу лодки, 2) человек на корме —и приравнять их друг другу, так как общий центр масс системы не переместился.

Определим абсциссу центра масс системы в начальное мгновение (рис. 175, в). Пусть центр массы лодки находится на расстоянии с₁ от носа. Тогда его абсцисса x₁₀ = (1,6 + c₁) м; х₂₀= 1,6 м. Подставляем в формулу (160):

Обращаем внимание на то, что при этом способе решения задач величины X1 и X2 являются уже не перемещениями точек, а их координатами.

В конечное мгновение, когда человек перейдет на корму (рис. 175, а), а лодка переместится ближе к берегу, общий центр масс всей системы останется на прежнем месте. При конечном положении лодки нос находится от начала координат на искомом расстоянии х. Тогда в этом положении x₁=x+c₁ и x₂ = x+3,6. Подставляя эти значения в формулу (160), получим

Приравниваем друг другу оба выражения абсциссы центра масс системы и находим положение лодки:
180 . 1,6= 180 x + 80 . 3,6, откуда х = 0.

Ответ. Лодка подойдет к берегу.

Задача №6

Сидящий в лодке охотник стреляет вперед в горизонтальном направлении. Пренебрегая трением воды, определить скорость лодки после выстрела, если до выстрела она была неподвижна; масса охотника 70 кг, масса лодки 30 кг, масса заряда 40 г и его начальная скорость 300 м/сек.

Решение. Механическое движение заряда передается в качестве механического же движения («отдача») на охотника и лодку. Примем, что механическая система состоит из двух точек: 1) лодка вместе с охотником и 2) заряд. Сила давления пороховых газов является внутренней по отношению к этой системе, давление газа в ружейном стволе во все стороны одинаково и, как было показано, сумма проекций внутренних сил на любую ось равна нулю. Внешних горизонтальных сил в системе нет. Проведя ось Ox горизонтально в направлении выстрела, получаем интеграл количества движения (171):

В начале выстрела, пока заряд еще не успел приобрести скорость, лодка тоже была неподвижна и, следовательно, C=0. В написанное выражение входят проекции абсолютных скоростей и, раскрывая знак суммы, получим

где υ₂-скорость лодки после выстрела, а (300 — υ₂)-абсолютная скорость заряда после выстрела, состоящая из разности скоростей (300 м/сек) заряда но стволу и скорости отдачи (υ₂).

Решая это уравнение, находим скорость отдачи.

Ответ. Лодка с охотником движется в сторону, противоположную выстрелу, со скоростью υ₂ = 0,12 м/сек.

Задача №7

Вода входит в неподвижный канал (рис. 176) переменного сечения» симметричный относительно вертикальной плоскости, со скоростью υ₀=2 м/ceκ под углом α₀=90° к горизонту; площадь сечения канала при входе 0,02 м 2 , скорость воды у выхода из канала υ_{1 =}4 м/сек и составляет угол α₁ — 30° с горизонтом. Определить горизонтальную составляющую реакции, которую вода оказывает на стенки канала.

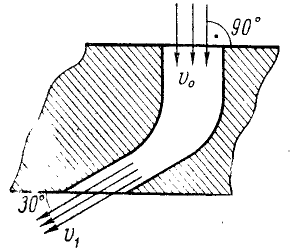
Рис. 176

Решение. Вода течет по каналу, меняя направление и величину своей скорости. Механическое движение воды не исчезает и не возникает вновь, меняется лишь вектор скорости. Требуется определить горизонтальную составляющую реакции, которую вода оказывает па стенки канала. Правильнее было бы назвать эту активную силу «давлением» воды на стенки канала. Все данные этой задачи относятся к воде, и мы будем определять горизонтальную составляющую реакции, оказываемой стенками канала на воду. Эта сила равна и противоположна искомой силе. Система единиц —СИ.

В плоскости симметрии канала проведем горизонтальную ось Ox и напишем уравнение (170)

В правой части 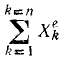есть сумма проекций на горизонтальную ось внешних сил, приложенных к системе (к воде). Единственной горизонтальной внешней силой является горизонтальная составляющая равнодействующей реакций стенок, т. е. та сила, которую мы должны определить. Эта сила при установившемся движении воды является постоянной. Поэтому

За время t в канал πocτyπaeт 0,02 м 2 . 2 м/сек . t ceκ = 0,04t м 3 = 40t π, или 40t кг воды:

Такое же количество воды покидает канал за то же время. Начальная и конечная скорости даны в условии. Подставляем все эти величины в (170):

Ответ.

Знак минус показывает, что по нашему чертежу проекция реакции отрицательна, т. е. направлена влево. Искомая в задаче горизонтальная составляющая давления на стенку имеет обратное направление—вправо. В задачнике II. В. Мещерского ответ приведен в килограммах. Чтобы перевести ньютоны в кГ, надо умножить число ньютонов на 0,102; имеем 138,4 . 0,102 = 14,1 кГ.

Давление струи

Задача №8

Определить давление струи воды на гладкую стенку, если скорость воды υ — 20 м/ceκ, сечение струп σ = 0,005 м 2 и струя направлена под углом α — 30° к стенке (рис. 177).

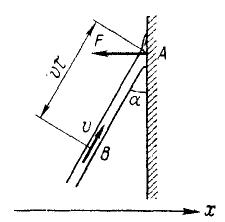
Рис. 177

Решение. Решим задачу сначала в общем виде. Отложим вдоль струн от стенки небольшой отрезок AB=υτ, где τ—малый промежуток времени. У конца В этого отрезка проведем поперечное сечение струи и рассмотрим движение системы частиц воды, находящихся в данное мгновение между этим сечением и стенкой. Общая масса всех частиц рассматриваемой системы m = 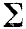mk=-σγυτ, где γ—масса 1 см 3 жидкости. До соприкосновения со стенкой частицы воды имеют общую скорость и, проекция которой на ось Ox (перпендикулярную стенке) υ_x = υ sin α. После соприкосновения со стенкой частицы движутся вдоль стенки и υ_x = 0.

На систему действует реакция F стенки, силой тяжести и давлением на выделенную часть струи со стороны следующих частиц струн, внешних по отношению к выделенной системе, пренебрегаем, так как они ври большой и незначительны но сравнению с F. Подставляя эти данные в (170), имеем

(173)

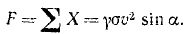
Этой формулой определяется давление нa стенку струи жидкости или сыпучего тела. Подставляя данные, находим ответ задачи.
Ответ. F = 102 кГ.

Ударом называют кратковременное взаимодействие тел, вызывающее за ничтожно малый промежуток времени резкое изменение скоростей их точек

Ударный импульс

Иногда материальные тела, находятся во взаимодействии всего лишь тысячные или даже стотысячные доли секунды, но при этом возникают настолько большие силы, что их импульс за столь малый промежуток времени достирает значительной величины и получается резкое, почти мгновенное изменение скоростей точек этих материальных тел. Такое кратковременное взаимодействие тел называют ударом, возникающие при этом силы называют ударными силами, а импульс ударной силы за время удара — мгновенным импульсом.

Ударные силы во многие тысячи раз превосходят вес ударяющего тела. Так, например, легким ударом молотка можно забить в деревянную стену гвоздь, но нужна громадная сила, чтобы тот же гвоздь вдавить, а не вбить в стену. Пуля, вес которой измеряется граммами, при выстреле пробивает доску, но пуля должна была бы весить многие тонны, чтобы сделать в доске такую же дырку своим весом. Поэтому за время удара пренебрегают весом тел и всеми прочими неударными («конечными») силами, пренебрегают перемещениями тел и считают, что векторы скоростей точек ударяющихся тел изменяются мгновенно.

«Количество движения системы никогда не изменяется от ударов при встрече ее тел» (Ньютон)

Прямой центральный удар двух тел

Пусть два тела движутся поступательно и прямолинейно со скоростями υ₁ и υ₂, причем центры масс C₁ и C₂ этих тел движутся по одной прямой, которую мы примем за ось Ох. В некоторое мгновение t первое тело, движущееся с большей скоростью, настигает второе и начинается удар, продолжающийся в течение малого отрезка времени τ_l. Пусть для каждого тела удар является центральным (т. е. мгновенный импульс проходит через центр масс тела) и прямым (т. е. относительные скорости точек соприкосновения тел перед ударом перпендикулярны к поверхности соприкасающихся тел в точке их соприкосновения). Предположим, что удар является неупругим (т. е. таким, при котором полученные за время удара деформации соударяющихся тел полностью сохраняются к концу удара). При отсутствии упругих сил тела не отталкиваются друг от друга и после удара продолжают двигаться с некоторой общей скоростью и. Определим мгновенный импульс S, действующий на каждое из тел со стороны другого. Для каждого из тел этот импульс является импульсом внешней реакции, и мы его легко определим, написав для каждого из тел уравнение (168′). В данном случае эти уравнения примут следующий вид:

(174)

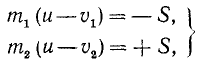
где m₁ и m₂—массы первого и второго тел, a υ₁ и υ₂— их скорости (выражаясь точнее, проекции их скоростей на прямую удара Ох) перед ударом. Из этих уравнений определим мгновенный импульс:

(175)

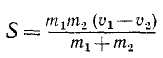
и скорость обоих тел после неупругого удара:

(176)

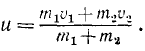
Если равенство (176) умножим на m₁ + m_2, то убедимся, что сумма количеств движения обоих тел при ударе не изменилась.

В природе не существует абсолютно неупругих тел и в действительности явление удара не заканчивается к тому мгновению, когда скорости тел становятся равными и. Во время удара тела стремятся восстановить свою первоначальную форму, они отталкиваются друг от друга и отдаляются, имея различные скорости u₁ и u₂.

Чтобы определить эти скорости и мгновенный импульс, разделим весь процесс удара на две стадии: 1) от начала соприкосновения тел до мгновения, при котором их скорости сравнялись, и 2) от этого мгновения до конца контакта. Удар, при котором полученные за время удара деформации соударяющихся тел частично сохраняются к концу удара, называют не вполне упругим.

Уравнения для первой стадии удара ничем не отличаются от только что полученных, мгновенный импульс определяется по (175) и скорость — по (176). Исходными уравнениями для второй стадии явятся те же уравнения (170), с той лишь разницей, что и будет в них играть роль начальной скорости, а конечными будут u₁ и u₂. Иным становится мгновенный импульс ударной реакции за эту вторую стадию удара. Обозначим его kS. Физическое значение коэффициента k, зависящего от упругих свойств соударяющихся тел, рассмотрим в дальнейшем. Имеем

(177)

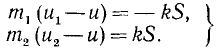
Из системы уравнений (174) и (177) найдем скорости не вполне упругих тел после удара:

Сложив два уравнения (174), а также два уравнения (177), в правых частях получим нуль. Приравнивая друг другу левые части сумм, получим

Таким образом, количество движения системы и при неупругом ударе не изменилось. Это объясняется тем, что для системы соударяющихся тел ударная сила является внутренней, а потому согласно интегралу количеств движения (171) .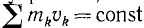

Отношение тангенсов угла падения и угла отражения равно коэффициенту восстановления:
k= tg α : tg β

Коэффициент восстановления

Из тех же уравнений (178) легко получить величину k, называемую коэффициентам восстановления. Имеем

(179)

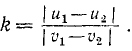
В числителе этого равенства мы видим относительную скорость тел после не вполне упругого удара, а в знаменателе—до удара. Величина k всегда положительна, поэтому взято отношение абсолютных величин относительных скоростей. Таким образом, коэффициент восстановления равен отношению модуля относительной скорости центров масс соударяющихся тел после прямого центрального удара к модулю относительной скорости их до удара.

Если маленький шарик ударяется о гладкую плиту под углом падения α≠0 (рис. 178), то, принимая удар за центральный и раскладывая движение по осям координат, заметим, что ударный импульс направлен перпендикулярно к гладкой плите, а потому проекция скорости шарика на гладкую плиту от удара не изменяется, но изменяется проекция скорости на нормаль к поверхности:

(180)

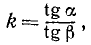
т. е. отношение тангенса угла падения к тангенсу угла отражения равно коэффициенту восстановления.

Движение точки переменной массы определяется уравнением И. В. Мещерского

Уравнение движения точки переменной массы

Пусть некоторая материальная точка M движется относительно неподвижной системы координат хОуz под действием силы . Предположим, что масса m точки M не остается постоянной, а изменяется, являясь, например, функцией времени, координат точки M, длины пройденного точкой пути, но не зависит от скорости точки:

В таком случае дифференциальные уравнения (125—127) не выражают движения точки М, так как в этих уравнениях tn

const. Дифференциальные уравнения, описывающие движения точки переменной массы, выведены И. В. Мещерским. Процесс изменения массы точки (или тела) он рассмотрел как присоединение к ней новых частиц («изменяющих масс») или как отделение от нее изменяющих масс. В случае присоединения изменяющие массы положительны, а в случае отделения—отрицательны.

Присоединение или отбрасывание масс возможно лишь при условии, что их скорости не равны скорости точки М. Поэтому в мгновение, в которое изменяющая масса отрывается от точки М или присоединяется к ней, между ними возникает мгновенное взаимодействие, аналогичное удару, изменяющее количество движения точки M. Однако это взаимодействие, конечно, не изменяет количества движения всей материальной системы, состоящей из точки M и изменяющих масс, так как внутренние силы не могут изменить количества движения системы.

Обозначим через ускорение, получаемое точкой M от присоединения или отбрасывания изменяющих масс, и через — ускорение точки М, от равнодействующей приложенных к ней сил, обусловленных другими материальными телами. Таким, образом, полное ускорение точки, M складывается из двух составляющих:

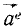
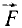
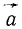
Руководствуясь принципом независимости действия сил, абстрагируемся от влияния внешних сил и найдем выражения для проекций на осн координат ускорения 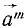сообщаемого точке M изменяющими массами.

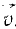
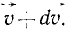
Пусть в мгновение t масса точки М равна m и ее абсолютная скорость равна V. Изменяющая масса dm в то же мгновение пусть имеет абсолютную скорость . Через бесконечно малый промежуток времени dt, когда изменяющая масса присоединится к точке М, их общая скорость vιιpn отсутствии внешних сил) станет равной Выразим по (159′) проекции количества движения системы до присоединения к точке M изменяющей массы:

и после присоединения:

Приравняем согласно (171) эти два выражения друг другу и после элементарных преобразований получим

Деля на dt, найдем проекцию ускорения на ось абсцисс:

Умножив это равенство на массу m, найдем проекцию прибавочной силы на ось Ox и аналогично на две другие оси:

Учитывая, что, кроме прибавочной силы и независимо от нее, на точку M действует сила F, проекции которой обозначим X, Y и Z, получим дифференциальные уравнения движения точки переменной массы (уравнения И. В. Мещерского):

(181)

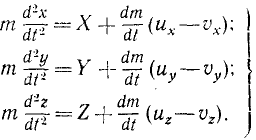
Эти равенства справедливы как при dm > 0, так и при dm / )

Задача №9

Определить скорость ракеты (точки переменной массы) при ее прямолинейном движении и без действия внешних сил, если относительная скорость выбрасываемых газов 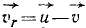постоянна и направлена противоположно скорости ракеты.

Решение. Направив ось Ox по скорости ракеты, напишем первое из уравнений Мещерского применительно к данному частному случаю:

Введем некоторые ограничения на изменение массы, а именно предположим, чтo масса m в каждое мгновение пропорциональна значению некоторой функции от времени: m=m₀f (t). При t = 0 масса m = m₀.

Интегрируя, получаем равенство, которое носит название формулы Циолковского.

Ответ. 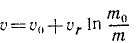. Это равенство правильнее называть задачей, а не формулой (см. В. В. Добронравов, H. Н. Никитин и А. П. Дворников, «Курс теоретической механики»).

Горизонтальное движение реактивного самолета

Задача №10

Определить закон движения x=x(t) самолета с жидкостным реактивным двигателем на активном и горизонтальном участке полета, положив, что масса самолета изменяется по линейному закону:

относительная скорость υ_r отбрасываемых частиц относительно самолета постоянна и аэродинамические силы зависят от квадрата скорости самолета, т. е. считать силу лобового сопротивления

и подъемную силу

Решение. Направим ось абсцисс горизонтально (рнс. 179) по скорости самолета, ось ординат перпендикулярно к ней.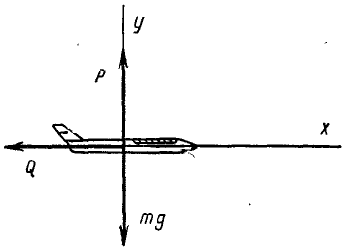

Рис. 179

На самолет по вертикальной оси действуют следующие силы: вес G и подъемная сила Р. При горизонтальном полете самолета они уравновешивают друг друга

По горизонтальной оси на самолет действуют сила лобового сопротивления, направленная против абсолютной скорости и прибавочная сила, направленная против относительной скорости υ_r, т. е. по движению самолета.

Движение самолета прямолинейное и горизонтальное, его можно описать одним (первым) из уравнений Мещерского (181). В этой задаче оно принимает вид:

Определим квадрат скорости из условия равенства вертикальных сил:

и подставим его в выражение силы лобового сопротивления

Для определения производной массы по времени, продифференцируем линейный закон изменения массы, заданный в условии задачи

Из того же закона видно, что

После подстановки найденных выражений в уравнение Мещерского и сокращения на m имеем:

Интегрируя один раз, получим:

Подставляем начальные данные (при t=0, υ_x=υ_0x), имеем

Получаем следующее выражение изменения скорости самолета в зависимости от времени

Чтобы получить закон движения самолета, надо в левой части этого выражения представить υ_x как производную от текущей координаты х по времени, разделить переменные и проинтегрировать

Возьмем отдельно последний интеграл

Определим C₂ по начальным данным, положив, что при t = 0 и х = 0, тогда

Подставив в предыдущее равенство вместо C₂ его значение 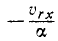найдем закон, определяющий движение самолета на активном участке пути. Естественно, что в эту формулу проекции входят со своими знаками, например, в рассмотренной задаче проекция относительной скорости υ_lx отрицательна, а проекция начальной скорости υox положительна.

Ответ.

• Момент количества движения
• Мощность и работа силы
• Потенциальная энергия
• Обобщенные координаты системы
• Координатный способ определения движения точки
• Касательное и нормальное ускорения точки
• Основные законы динамики
• Колебания материальной точки

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Импульс системы материальных точек уравнение движения центра масс

Рассмотрим систему материальных точек массами `m_1`, `m_2«. `, движущихся в произвольной ИСО со скоростями `vecv_1`, `vecv_2«. `. Импульсом `vecP_(«c»)` системы материальных точек называют векторную сумму импульсов материальных точек, составляющих систему, `vecP_(«c») = vecp_1 + vecp_2 + . `.

Найдём скорость `(Delta vecP_(«c»))/(Delta t)` изменения импульса системы материальных точек (ответ на такой вопрос для одной материальной точки нам известен). Для примера рассмотрим систему двух материальных точек. Будем считать, что на первую материальную точку действуют суммарной силой `vecF_1` внешние по отношению к системе тела и внутренняя сила `vecf_(12)` со стороны второго тела. В свою очередь, на вторую материальную точку действуют внешние по отношению к системе тела, сумма этих сил `vecF_2`, и внутренняя сила `vecf_(21)` со стороны первого тела. Тогда с учётом второго закона Ньютона для каждого тела получаем

`(Delta vecP_(«c»))/(Delta t) = (Delta vecp_1)/(Delta t) + (Delta vecp_2)/(Delta t) = (vecF_1 + vecf_(12)) + (vecF_2 + vecf_(21))`.

По третьему закону Ньютона `vecf_(12) + vecf_(21) = vec 0`, и мы приходим к теореме об изменении импульса системы материальных точек

`(Delta vecP_(«c»))/(Delta t) = vecF_1 + vecF_2`,

скорость изменения импульса системы материальных точек равна векторной сумме всех внешних сил, действующих на систему.

Из приведённого доказательства следует, что третий закон Ньютона можно сформулировать и как требование сохранения импульса системы взаимодействующих тел, если нет никаких других внешних сил. В этом — его более глубокое физическое содержание.

Клин массой `M` находится на шероховатой горизонтальной поверхности стола. На клин положили брусок массой `m` и отпустили. Брусок стал соскальзывать, а клин остался в покое. Коэффициент трения скольжения бруска по поверхности клина равен `mu`, наклонная плоскость клина составляет с горизонтом угол `alpha`. Найдите горизонтальную `R_1` и вертикальную `R_2` силы (рис. 9), с которыми клин действует на опору.

По третьему закону Ньютона искомые силы связаны с силой трения `vecR_1 =- vecF_(«тр»` и силой нормальной реакции `vecR_2 =- vecN_(«г»)`, действующими на клин со стороны опоры (рис. 10). Силы `vec(F_sf»тр»)` и `vec(N_sf»г»)`, наряду с силами тяжести, являются внешними по отношению к системе «клин + брусок» и определяют скорость изменения импульса этой системы.

Импульс `vecP_(«c»)` системы направлен по скорости бруска и по величине равен произведению массы бруска на его скорость `vecP_(«c») = vec p = m vec v (t)`. Для определения скорости изменения импульса `vec p` бруска обратимся ко второму закону Ньютона (рис. 11):

`(Delta vecp)/(Delta t) = m vec g + vec N + vec(f_sf»тр»`.

Переходя к проекциям приращений импульса бруска и сил на оси `Oy` и `Ox` с учётом соотношения `f_sf»тр» = mu N`, получаем

`(Delta p_y)/(Delta t) = 0 = N — mg cos alpha`, `(Delta p_x)/(Delta t) = mg(sin alpha — mu cos alpha)`.

По теореме об изменении импульса системы «клин + брусок»

`(Delta vecP_(«c»))/(Delta t) = M vec g + m vec g + vecN_(«г») + vecF_(«тр»)`.

Переходя в последнем равенстве к проекциям на горизонтальное и вертикальное направления с учётом

Отсюда находим искомые силы

`R_1 = F_sf»тр» = mg(sin alpha — mu cos alpha) cos alpha`,

`R_2 = N_sf»г» = (M + m) g — mg(sin alpha — mu cos alpha) sin alpha`.