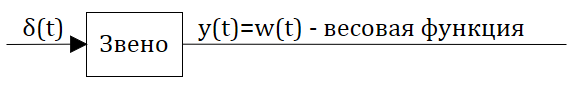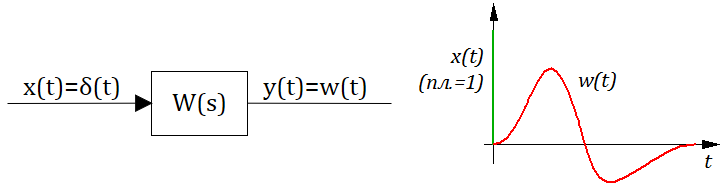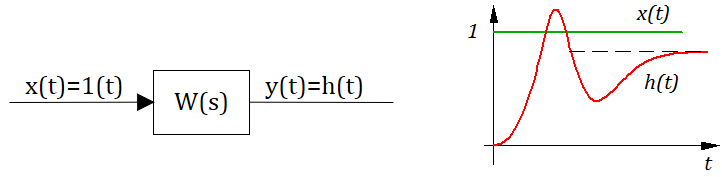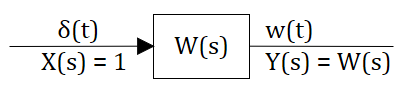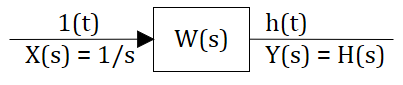Интеграл дюамеля и уравнение свертки


20.2. ВРЕМЕННОЙ МЕТОД РАСЧЕТА ПЕРЕХОДНЫХ ПРОЦЕССОВ. ИНТЕГРАЛ СВЕРТКИ. ИНТЕГРАЛ ДЮАМЕЛЯ
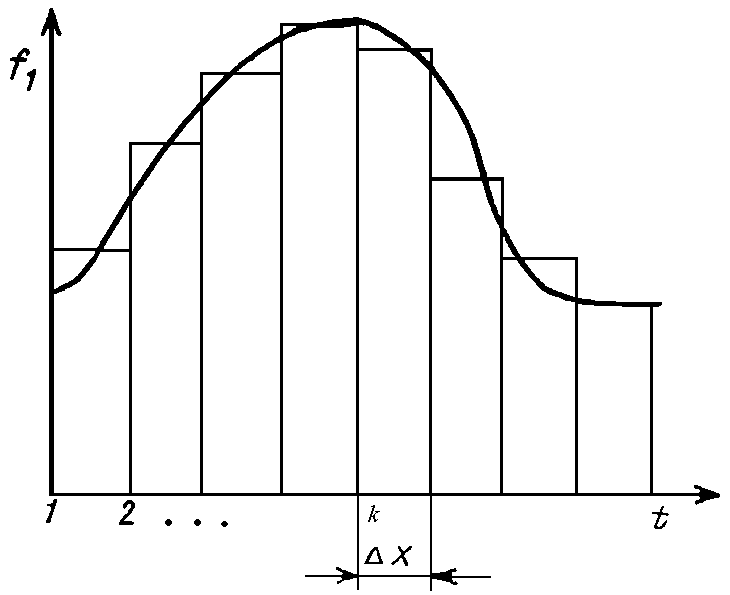
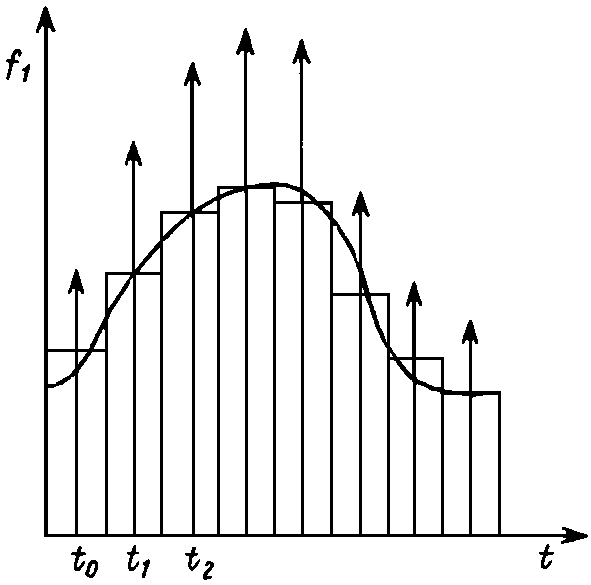
Рассмотрим процесс в цепи при действии на ее входе сигнала произвольной формы f 1 ( t ) (рис. 20.3). Этот сигнал можно представить в виде последовательности прямоугольных импульсов длительностью D x с амплитудами f 1 ( k D x ).
При малых значениях D x каждый такой импульс эквивалентен действию на цепь d -импульса, включаемого в момент t = k D x и имеющего площадь f 1 ( k D x ) D x . Поэтому входной сигнал представим в виде суммы 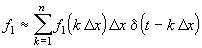
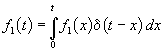
Поскольку реакция цепи на каждый d -импульс описывается импульсной характеристикой h d , то для выходной величины f 2 ( t ) можно записать аналогичный интеграл, в котором реакция на входной импульс d ( t – x ) выражена как h d ( t – x ):
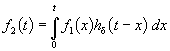
Полученный интеграл называется интегралом свертки и используется при вычислении реакции цепи f 2 ( t ) на воздействие f 1 ( t ) произвольной формы. Он и является основой временнóго метода расчета переходных процессов.
Как уже отмечалось, указанные выше пределы интегрирования требуют уточнения, особенно, при наличии в подынтегральных сомножителях слагаемых в виде d -функций. При вычислении интеграла свертки необходимо учитывать, что первый сомножитель под интегралом f 1 ( x ) = 0 при x h d ( t – x ) = 0 при t – x x > t + 0. Именно эти значения пределов интегрирования (– 0 x t f 1 d -слагаемое может содержаться в h d ( t – x ). Вклад этого слагаемого можно учесть отдельно. Для этого запишем
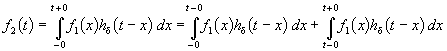
Так как второй интеграл можно преобразовать к виду 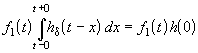
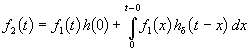
В последнем выражении под интегралом учитывается только ограниченная часть импульсной характеристики h d .
Пример использования интеграла свертки рассмотрен в Задаче 17.1.
Основные свойства интеграла свертки.
1. Поскольку при t f 1 ( t ) и h d ( t ) º 0, то пределы в интеграле свертки можно взять от — ¥ до ¥ , то есть
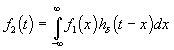
так как на добавленных отрезках (– ¥ , 0) и ( t , ¥ ) один из подынтегральных сомножителей тождественно равен нулю.
2. Переменные интегрирования можно заменять, используя связь t – x = y . Интеграл при этом примет вид
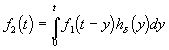
Операция свертки растягивает импульсный сигнал во времени. Пусть прямоугольный импульс A длительностью T (рис. 20.4, а ) действует на входе цепи, импульсная характеристика которой изображена на рис. 20.4, б . Такая цепь представляет интегратор с конечным временем интегрирования t .
В этом простом случае результат свертки легко найти графически. Пусть для определенности T > t , тогда для различных моментов времени t 1 , t 2 и t 3 произведение f 1 на h ( t – x ) будет определяться площадью перекрывающихся прямоугольников (рис. 20.4, в ), и выходной сигнал будет иметь вид, показанный на рис. 20.4, г . Таким образом, цепь суммирует длительность импульса T и собственное время t .
Интеграл Дюамеля. Интеграл свертки можно выразить через переходную характеристику. Это приводит к интегралу Дюамеля. Для его получения используем записанную п. 20.1 связь h d = dh / dt , из которой произведение h d ( t – x ) dx можно представить как – dh ( t – x ):
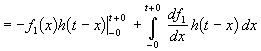
В последнем преобразовании использована формула интегрирования по частям. Так как внеинтегральный член равен нулю, то окончательно получим
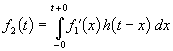
где 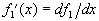
Неудобство этого выражения связано с d -слагаемыми в 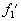
Последнее выражение является наиболее распространенной формой записи интеграла Дюамеля.
Если входная функция f 1 имеет разрывы, то для расчета переходного процесса временным методом удобнее использовать интеграл свертки, если она непрерывна, то интеграл Дюамеля (при неограниченной характеристике h d ).
При выполнении расчетов временным методом следует обращать внимание на: 1) различное аналитическое описание функции f 1 на различных отрезках у импульсов сложной формы; 2) правильный учет неограниченного характера функции h d (при вычислении интегралов с d- слагаемыми); 3) правильный учет разрывов функции f 1 в интеграле Дюамеля.
Пример расчета переходного процесса с помощью интеграла Дюамеля рассмотрен в Задачe 17.2.
Особенности применения операторного метода при определении «последействия» импульса. Реакция цепи на одиночный импульс длительностью Т при t > Т содержит лишь свободные составляющие процесса, соответствующие корням характеристического уравнения цепи. В связи с этим при использовании операторного метода нахождение оригинала по теореме разложения требует учета не всех корней знаменателя изображения реакции, а лишь тех из них, которые являются корнями знаменателя передаточной функции. Это существенно упрощает расчет, особенно для импульсов сложной формы. Пусть определено изображение импульса с конечной длительностью
(f1(t) = 0 при t > T). При воздействии такого импульса на цепь с передаточной функцией K( s) = Q(s)/P(s) реакция при t > Т содержит лишь экспоненты е s k t с показателями, в которые входят корни P(s) =0. Поэтому для реакции при t > Т по теореме разложения имеем
(предполагается отсутствие кратных корней s k) .
Рассмотрим в качестве примера Задачу 17.1. Передаточная функция цепи имеет выражение K( s) = s t /(l + s t ). Операторное изображение входного сигнала имеет вид
Поэтому изображение выходного напряжения равно
что совпадает с результатом, полученным в Задаче 17.1.
Если воздействующий импульс f1(t) не имеет простого аналитического описания, то его представляют в виде совокупности импульсов прямоугольной формы с амплитудой f1(tk) длительностью D tk, каждый из которых рассматривается как d -импульс
С помощью теоремы запаздывания получим изображение входного сигнала F1(s)
При таком представлении временной метод приводит к замене интеграла свертки суммой; для выходного сигнала будем иметь
Интеграл дюамеля и уравнение свертки
Зная реакцию цепи на единичное возмущающее воздействие, т.е. функцию переходной проводимости 

При использовании интеграла Дюамеля для разделения переменной, по которой производится интегрирование, и переменной, определяющей момент времени, в который определяется ток в цепи, первую принято обозначать как 
Пусть в момент времени 



В момент времени t составляющая общего тока, определяемая начальным скачком напряжения 

В момент времени 


Полный ток 


Заменяя конечный интервал приращения времени 
 . . | (1) |
Соотношение (1) называется интегралом Дюамеля.
Следует отметить, что с использованием интеграла Дюамеля можно определять также напряжение. При этом в (1) вместо переходной проводимости 
Последовательность расчета с использованием
интеграла Дюамеля
- Определение функции
(или
) для исследуемой цепи.
- Запись выражения
(или
) путем формальной замены t на
.
- Определение производной
.
- Подстановка найденных функций в (1) и интегрирование определенного интеграла.
В качестве примера использования интеграла Дюамеля определим ток в цепи рис. 3, рассчитанный в предыдущей лекции с использованием формулы включения.
Исходные данные для расчета: 



 .
. .
.

Полученный результат аналогичен выражению тока, определенному в предыдущей лекции на основе формулы включения.
Метод переменных состояния
Уравнения элекромагнитного состояния – это система уравнений, определяющих режим работы (состояние) электрической цепи.
Метод переменных состояния основывается на упорядоченном составлении и решении системы дифференциальных уравнений первого порядка, которые разрешены относительно производных, т.е. записаны в виде, наиболее удобном для применения численных методов интегрирования, реализуемых средствами вычислительной техники.
Количество переменных состояния, а следовательно, число уравнений состояния равно числу независимых накопителей энергии.
К уравнениям состояния выдвигаются два основных требования:
-возможность восстановления на основе переменных состояния (переменных, относительно которых записаны уравнения состояния) любых других переменных.
Первое требование удовлетворяется специальной методикой составления уравнений состояния, которая будет рассмотрена далее.
Для выполнения второго требования в качестве переменных состояния следует принять потокосцепления (токи в ветвях с индуктивными элементами) и заряды (напряжения) на конденсаторах. Действительно, зная закон изменения этих переменных во времени их всегда можно заменить источниками ЭДС и тока с известными параметрами. Остальная цепь оказывается резистивной, а следовательно, всегда рассчитывается при известных параметрах источников. Кроме того, начальные значения этих переменных относятся к независимым, т.е. в общем случае рассчитываются проще других.
При расчете методом переменных состояния, кроме самих уравнений состояния, связывающих первые производные 



Таким образом, полная система уравнений в матричной форме записи имеет вид
 ; ; | (2) |
 . . | (3) |
Здесь 







Начальные условия для уравнения (2) задаются вектором начальных значений 
В качестве примера составления уравнений состояния рассмотрим цепь на рис. 4,а, в которой требуется определить токи 

По законам Кирхгофа для данной цепи запишем
 ; ; | (4) |
 ; ; | (5) |
 . . | (6) |
Поскольку 
или в матричной форме записи
Матричное уравнение вида (3) вытекает из соотношений (4) и (6):
Вектор начальных значений 

Непосредственное использование законов Кирхгофа при составлении уравнений состояния для сложных цепей может оказаться затруднительным. В этой связи используют специальную методику упорядоченного составления уравнений состояния.
Методика составления уравнений состояния
Эта методика включает в себя следующие основные этапы:
1. Составляется ориентированный граф схемы (см. рис. 4,б), на котором выделяется дерево, охватывающее все конденсаторы и источники напряжения (ЭДС). Резисторы включаются в дерево по необходимости: для охвата деревом всех узлов. В ветви связи включаются катушки индуктивности, источники тока и оставшиеся резисторы.
2. Осуществляется нумерация ветвей графа (и элементов в схеме), проводимая в следующей последовательности: первыми нумеруются участки графа (схемы) с конденсаторами, затем резисторами, включенными в дерево, следующими нумеруются ветви связи с резисторами и, наконец, ветви с индуктивными элементами (см. рис. 4,б).
3. Составляется таблица, описывающая соединение элементов в цепи. В первой строке таблицы (см. табл. 1) перечисляются емкостные и резистивные элементы дерева, а также источники напряжения (ЭДС). В первом столбце перечисляются резистивные и индуктивные элементы ветвей связи, а также источники тока.
2. Математическое описание систем автоматического управления ч. 2.9 — 2.13
Лекции по курсу «Управление Техническими Системами», читает Козлов Олег Степанович на кафедре «Ядерные реакторы и энергетические установки», факультета «Энергомашиностроения» МГТУ им. Н.Э. Баумана. За что ему огромная благодарность.
Данные лекции только готовятся к публикации в виде книги, а поскольку здесь есть специалисты по ТАУ, студенты и просто интересующиеся предметом, то любая критика приветствуется.
В предыдущих сериях:
В это части будут рассмотрены:
2.9. Использование обратных преобразований Лапласа для решения уравнений динамики САР (звена).
2.10. Весовая и переходная функции звена (системы).
2.11. Определение переходного процесса в системе (САР) (звене) через весовую и переходную функции.
2.12. Mетод переменных состояния.
2.13. Переход от описания переменных «вход-выход» к переменным состояния.
Попробуем применить, полученные знания на практике, создавая и сравнивая расчетные модели в разных видах. Будет интересно познавательно и жестко.
2.9. Использование обратных преобразований Лапласа для решения уравнений динамики САР (звена)
Рассмотрим динамическое звено САР изображенное на рисунке 2.9.1
Предположим, что уравнение динамики имеет вид:
где: — постоянные времени;
— коэффициент усиления.
Пусть известны отображения:
Найдем изображения для производных:
Подставим полученные выражения в уравнение динамики и получим уравнение динамики в изображениях:
B(s) — слагаемое, которое определяется начальными условиями, при нулевых начальных условиях B(s)=0.
W(s) — передаточная функция.
Передаточной функцией САР (звена) называется отношение изображений выходного сигнала к входному воздействию при нулевых н.у.
После того, как в явном виде найдено изображение для неизвестной выходной величины, нахождение оригинала не представляет сложностей. Либо по формуле Хэвисайда, либо разложением на элементарные дроби, либо по таблице из справочника.
Пример
Построить выходной сигнал звена САР при единичном входном воздействии и нулевых начальных условиях, если уравнение динамики звена имеет следующий вид:
входное воздействие: — единичное ступенчатое воздействие.
Выполним преобразование Лапласа:
Подставим в уравнение динамики и получим уравнение динамики в изображениях:
Для получения выходного сигнала из уравнения в изображениях выполним обратное преобразования Лапласа:
2.10. Весовая и переходная функции звена (системы).
Определение: Весовой функцией звена (системы) называется реакция системы при нулевых н.у. на единичное импульсное воздействие.
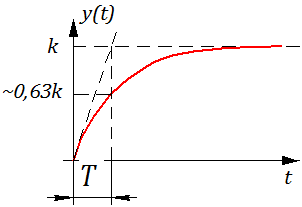
Определение: Переходной функцией звена (системы) при н.у. называется реакция на единичное ступенчатое воздействие.
На этом месте можно вспомнить, что преобразование Лапласа это интеграл от 0 до бесконечности по времени (см. предыдущий текст), а импульсное воздействие при таком интегрировании превращается в 1 тогда в изображениях получаем что:
Передаточная функция играет роль изображения реакции звена или системы на единичное импульсное воздействие.
Для единичного ступенчатого воздействия преобразование Лапласа тоже известно (см. предыдущий текст):
тогда в изображениях получаем, что реакция системы на ступенчатое воздействие, рассчитывается так:
Реакция системы на единичное ступенчатое воздействие рассчитывается обратным преобразованием Лапласа:
2.11. Определение переходного процесса в системе (САР) (звене) через весовую и переходную функции. Формула Дюамеля-Карсона
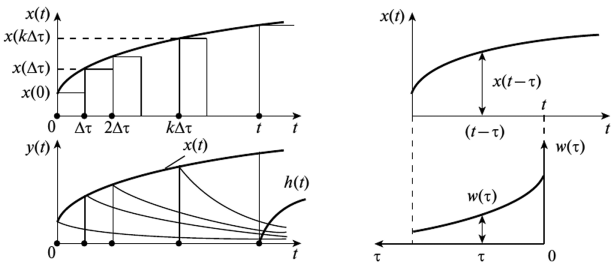
Предположим, что на вход системы поступает произвольное воздействие x(t), заранее известное. Найти реакцию системы y(t), если известны входное воздействие x(t) и весовая функция w(t).
Представим, что входное воздействие представляет собой последовательность прямоугольных импульсов до времени t и ступеньки высотой x(t) в момент времени t. см.рис. 2.11 Для каждого импульса мы можем записать реакцию системы через весовую функциию:
где:
— значение отклика по завершению предыущего импульса;
— время завершения текущего импульса;
— значение весовой функции в начале текущего импульса.
Тогда для определения занчения отклика в произвольный момент времени необходимо сложить все импульсы и ступенчатое воздействие в момент времени t:
Переходя к пределам
если перейти от t к бесконечности мы получим формулу интеграла Дюамеля-Карсона, или по другому «интеграла свертки» который обеспечивает вычисление оригинала функции по произвдению изображения двух функций:
где — вспомогательное время
Для вывода аналогичной зависмости от переходной функции вспомним что изображение весовой и переходной функции связаны соотношением: запишем выражение изображения для отклика в операторной форме:
Используя интеграл свертки получаем, что при известной переходной функции (h(t)) и известному входному воздействию х(t) выходное воздействие рассчитывается как:
2.12. Mетод переменных состояния.
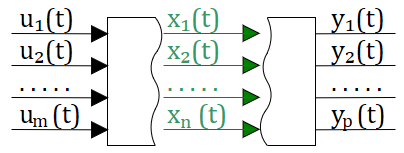
До этого мы рассматривали системы с одной передаточной функцией, но жизнь всегда сложнее и как правило в системах есть несколько передаточных функций несколько входных воздейстий и несколько реакций системы. (см. рис. 2.12.1)
В этом случае наиболее удобной формой пердставления систем для их анализа и расчета оказался метод переменных состояния. Для этого метода, вместо передаточных функций связывающих вход с выходом используются дополнительные переменные состояния, которые описывают систему. В этом случае можно говорить, что состояние системы — это та минимальная информация о прошлом, которая необходима для полного описания будущего поведения (т.е. выходов) системы, если поведение ее входов известно. см. рис. 2.12.2
В методе состояний, производные всех переменных состояния, в общем случае зависит от всех переменных и всех входных воздействия, и могут быть записаны в представленной ниже системы обыкновенных дифференциальных уравнений (ОДУ) первой степени. Эта система уравнений называю системой ОДУ в форме Коши:
Выход из системы зависит от переменных состояния и, в общем случае от входных воздействий и описывается следующей системой уравнений:
где:
n — количество перемнных состояния,
m — количество входных воздействий,
p — количество выходных переменных;
Данная система уравнений может быть записана в матричной форме:
где:
— вектор входа (или вектор управления);
— вектор столбец производных переменных состояния;
— вектор столбец переменных состояния;
— вектор выхода;
— собственная матрица системы [n x n],
— постоянные коэффициенты;
— матрица входа [n x m],
— постоянные коэффициенты;
— матрица выхода а [p x n],
— постоянные коэффициенты;
— матрица обхода [p x m],
— постоянные коэффициенты;
В нашем случае почти всегда все элементы матрицы D будут нулевыми: D = 0.
Такое описание системы позволяет с одной стороны стандартным образом описывать различные технические системы. Явная формула для расчета производных позволяет достаточно просто осуществлять численное интегрирование по времени. И это используется в различных программах моделирования
Другое использование данного представления для простых систем, описанных в переменных «вход-выход», зачастую позволяет устранить технические трудности, связанные с решением ОДУ высокой степени.
Еще одним преимуществом данного описания, является то, что уравнения в форме Коши можно получить из законов физики
Пример решения задачи в форме коши.
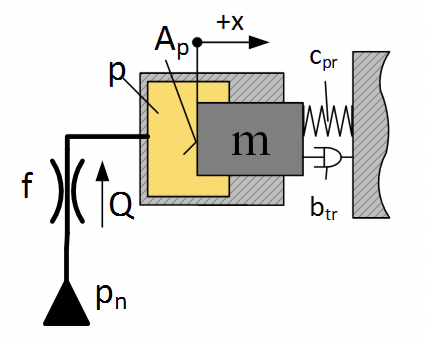
Рассмотрим задачу моделирования гидравлического привода, при следующих условиях:
Дано:
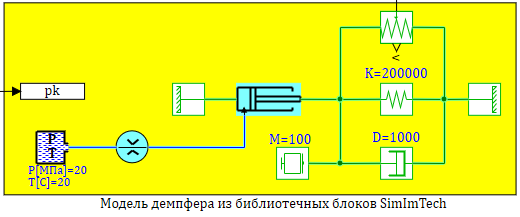
Цилиндрический плунжер диаметром 10 мм, с приведенной массой 100 кг, работает на пружину жесткостью 200 Н/мм и демпфер с коэффициентом вязкого трения — 1000 Н/(м/с). Полость начальным объемом 20 см 3 соединяется с источником давлния дросселем диаметром диаметр которого 0,2 мм. Коэффициент расхода дросселя 0.62. Плотность рабочей жидкости ρ = 850 кг/м 3 .
Определить:
Перемещение дросселя, если в источнике давление происходит скачек 200 бар. см. рис. 2.12.13
Уравенение движение плунжера:
Где: – площадь плунжера,
– жесткость пружины,
– коэффициент вязкого трения, p – давление в камере.
Поскольку дифференциальное движения это уравнение второго порядка, превратим его в систему из двух уравнений первого порядка, добавив новую переменную — скорость , тогда
Уравнение давления в камере, для упрощения принимаем что изменениям объема камеры из-за перемещения плунжера можно пренебречь:
Где: Q – расход в камеру, V — объем камеры.
Расход через дроссель:
Где: f– площадь дросселя, – давление в источнике, p – давление в камере.
Уравнение дросселя не линейное, по условию задачи, давление входное изменяется скачком, от 0 до 200 бар, проведем линеаризацию в окрестности точки давления 100 бар тогда:
Подставляем линеаризованную формул расхода в формулу давления:
Таким образом общая система уравнений в форме Коши, для рис 2.12.3 привода принимает вид:
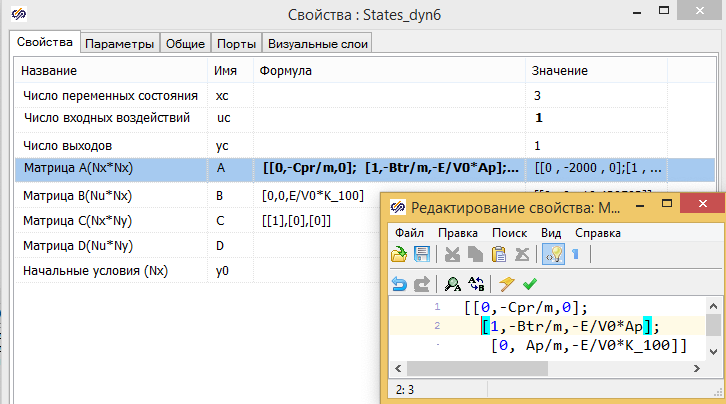
Матрицы A, B, С, В для матричной формы системы уравнений принимают вид:
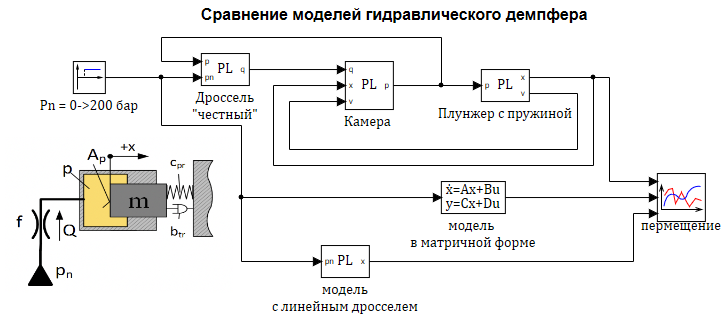
Проверим моделированием в SimInTech составленную модель. На рисунке 2.12.13 представлена расчетная схема содержащая три модели:
1 — «Честная» модель со всеми уравнениями без упрощений.
2 — Модель в блоке «Переменные состояние» (в матричной форме).
3 — Модель в динамическом блоке с линеаризованным дросселем.
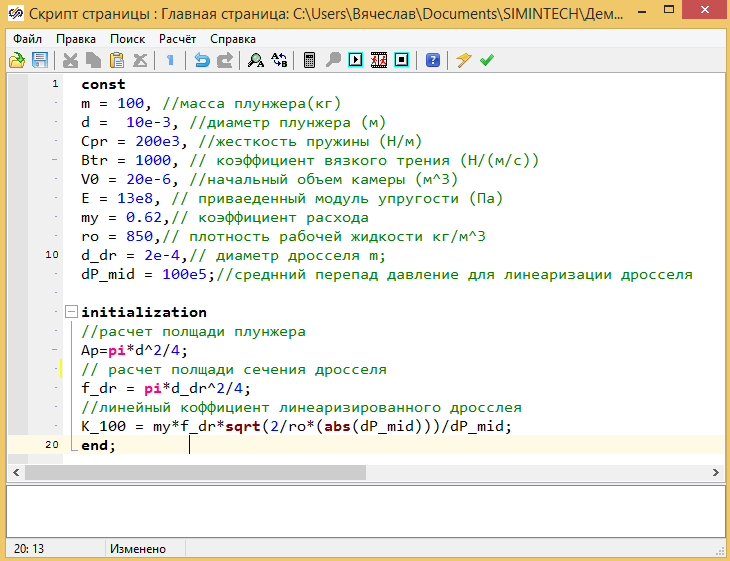
Все условия задачи задаются как глобальные константы проекта, в главном скрипте проекта, там же расчитываются на этапе инициализации расчета, площади плунжера и проходного сечения дросселя см. рис. 2.12.5:
Рисунок 2.12.5 Глобальный скрипт проекта.
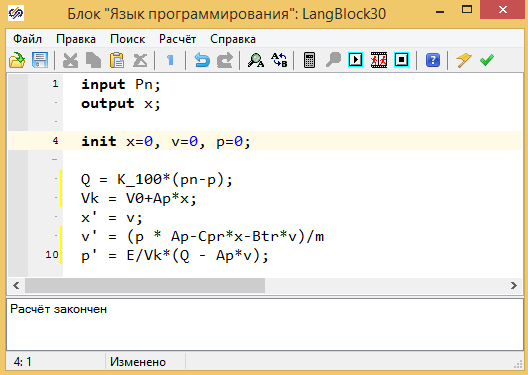
Модель на внутреннем языке программирования представлена на рис. 2.12.6. В данной модели используется описание модели в форме Коши. Так же выполняется учет изменения объема дросселя на каждом шаге расчета, за счет перемещения плунжера (Vk = V0+Ap*x.)
Рисунок 2.12.6 Скрипт расчета модели в форме Коши.
Модель в матричном форме задается с использованием глобальных констант в виде формул. (Матрица в SimInTech задается в виде последовательности из ее столбцов) см. рис. 2.12.7
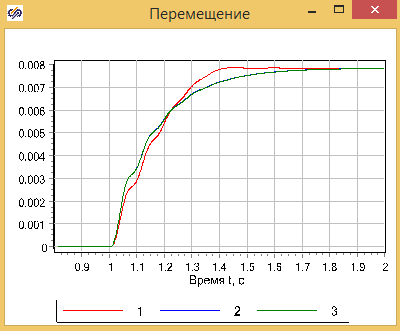
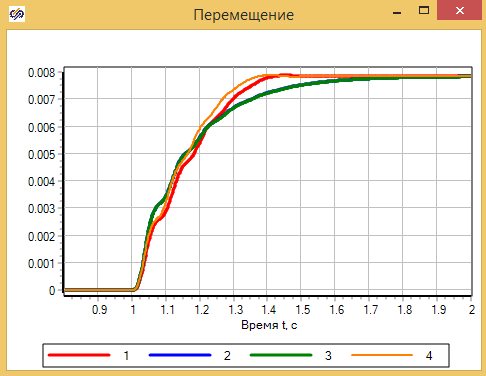
Результаты расчета показывают, что модель в матричной форме и модель на скриптовом языке в форме Коши, практически полностью совпадают, это означает, что учет изменения объема полости практически не влияют на результаты. Кривые 2 и З совпадают.
Процедура линеаризация расхода через дроссель вызывает заметное отличие в результатах. 1-й график c «честной» моделью дросселя, отличается от графиков 2 и 3. (см. рис. 2.12.8)
Сравним полученные модели, с моделью созданной из библиотечных блоков SimInTech, в которых учитываются так же изменение свойств реальной рабочей жидкости — масла АМГ-10. Сама модель представлена на рис. 2.12.9, набор графиков на рисунке 2.12.10
На графиках видно, что уточненная модель отличается от предыдущих, однако погрешность модели составлят наших упрощенных моделей составляют примерно 10%, в лишь в некоторые моменты времени.
2.13. Переход от описания переменных «вход-выход» к переменным состояния и обратно
Рассмотрим несколько вариантов перехода от описания «вход-выход», к переменным состояния:
Вариант прехода зависит от правой части уравнения с переменными «вход-выход»:
2.13.1. Правая часть содержит только b0*u(t)
В этом варианте, в уравнениях в правой части отсутствуют члены с производными входной величины u(t). Пример с плунжером выше так же относится к этому варианту.
Что бы продемонстрировать технологию перехода рассмотрим следующее уровнение:
Для перехода к форме Коши ведем новые переменные:
И перепишем уравнение относительно y»'(t):
Используя эти переменные можно перейти от дифференциального уравнения 3-го прядка, к системе из 3-х уравнений первого порядка в форме Коши:
Соотвественно матрицы для матричного вида уравнений в переменных сосотяния:
2.13.2. Правая часть общего вида
Более сложный случай, когда в уравнениях есть производные от входных воздействий и уравнение в общем случае выглядит так:
Сделаем преобразования: перейдем к уравнениям динамики в изображениях:
Тогда можно представить уравнение в изображениях в виде:
Разделим уравнение в изображениях на произведение полиномов , получим:
Где: — некоторая комплексная величина (отношение двух комплексных величин). Можно считать, что
отображение величины
. Тогда входная величина может быть в изображениях представлена как:
Вренемся к оригиналу от изображений получим: ,
где: — дифференциальный оператор.
А это дифференциальное уравнение n-го порядка мы можем преобразовать к системе из n дифференциальных уравнений первого порядка, как это мы делали выше:
Таким образом, мы получили систему уравнение в форе Коши, относительно переменных состояния :
А регулируемую величину (выход системы) мы так же можем выразить через эти переменные, в изображениях:
Перейдем от изображения к оригиналам:
Если обозначить вектор , то мы получим уравнения переменных состояниях в матричной форме, где D = 0:
Пример:
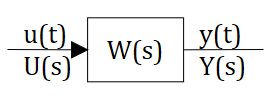
Рисунок 2.13.1 Передаточная функция.
Имеется передаточная функция (рис. 2.13.1) в изображениях :
Необходимо преобразовать передаточную функцию к системе уравнений в форме Коши
В изображения реакция системы связана с входным воздействие соотношением:
Разделим в последнем правую и левую часть на произведения , и введем новую перменную
:
Полиномы N(s) и L(s) равны:
Перейдем в последнем выражении от изображения к оригиналам и ведем новые переменные (состояния):
Переходим от уравнения третьего порядка к системе трех уравнений первого порядка:
Или в матричной форме:
Для получения второго матричного уравнения воспользуемся соотношением для новых переменных в отображениях:
Перейдем от изображений к оригиналу:
Таким образом второе уравнение матричной системы выглядит так:
Проверим в SimInTech сравнив передаточную функцию и блок переменных состояния, и убедимся, что графики совпадают см. рис. 2.13.2
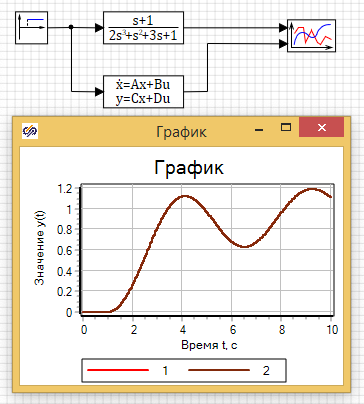
Рисунок 2.13.2 Сравнение переходного процеса у блока передаточной функции и блока переменных состояния.
http://toehelp.ru/theory/toe/lecture29/lecture29.html
http://habr.com/ru/post/520770/

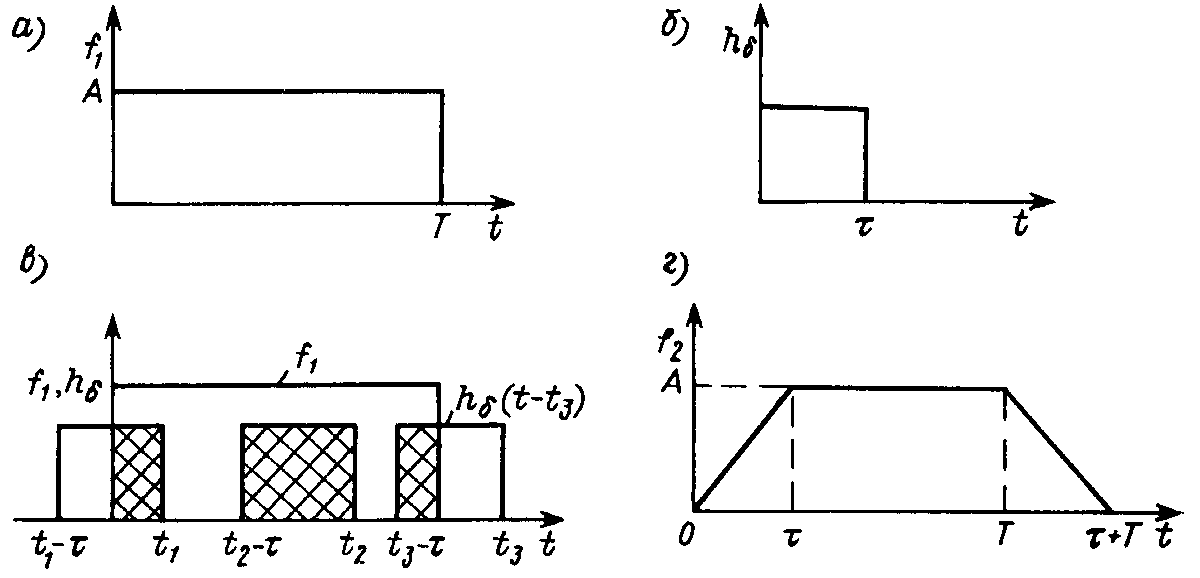
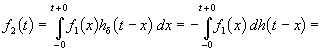
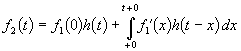
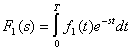
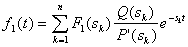
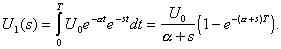
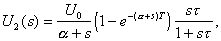
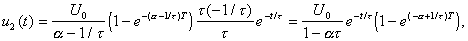
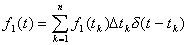
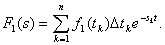

 (или
(или  ) для исследуемой цепи.
) для исследуемой цепи. (или
(или  ) путем формальной замены t на
) путем формальной замены t на  .
. .
.