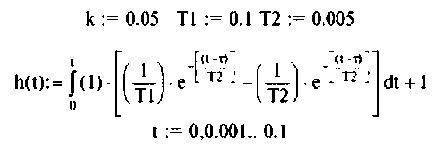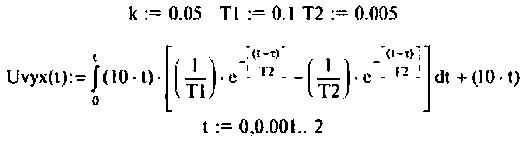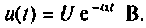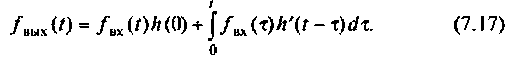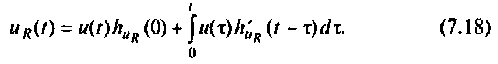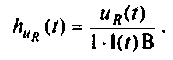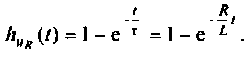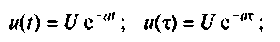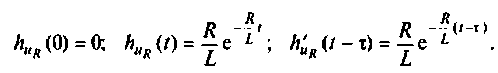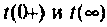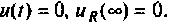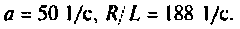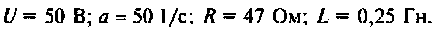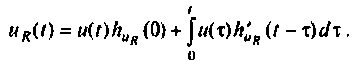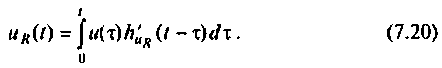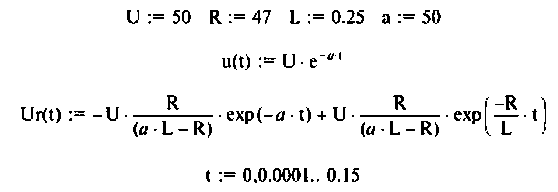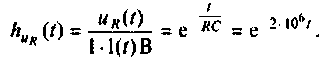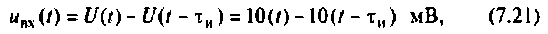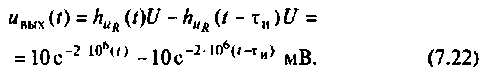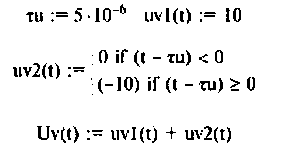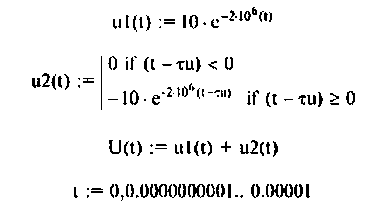Интеграл дюамеля и уравнение свертки записывается в виде
Зная реакцию цепи на единичное возмущающее воздействие, т.е. функцию переходной проводимости 

При использовании интеграла Дюамеля для разделения переменной, по которой производится интегрирование, и переменной, определяющей момент времени, в который определяется ток в цепи, первую принято обозначать как 
Пусть в момент времени 



В момент времени t составляющая общего тока, определяемая начальным скачком напряжения 

В момент времени 


Полный ток 


Заменяя конечный интервал приращения времени 
 . . | (1) |
Соотношение (1) называется интегралом Дюамеля.
Следует отметить, что с использованием интеграла Дюамеля можно определять также напряжение. При этом в (1) вместо переходной проводимости 
Последовательность расчета с использованием
интеграла Дюамеля
- Определение функции
(или
) для исследуемой цепи.
- Запись выражения
(или
) путем формальной замены t на
.
- Определение производной
.
- Подстановка найденных функций в (1) и интегрирование определенного интеграла.
В качестве примера использования интеграла Дюамеля определим ток в цепи рис. 3, рассчитанный в предыдущей лекции с использованием формулы включения.
Исходные данные для расчета: 



 .
. .
.

Полученный результат аналогичен выражению тока, определенному в предыдущей лекции на основе формулы включения.
Метод переменных состояния
Уравнения элекромагнитного состояния – это система уравнений, определяющих режим работы (состояние) электрической цепи.
Метод переменных состояния основывается на упорядоченном составлении и решении системы дифференциальных уравнений первого порядка, которые разрешены относительно производных, т.е. записаны в виде, наиболее удобном для применения численных методов интегрирования, реализуемых средствами вычислительной техники.
Количество переменных состояния, а следовательно, число уравнений состояния равно числу независимых накопителей энергии.
К уравнениям состояния выдвигаются два основных требования:
-возможность восстановления на основе переменных состояния (переменных, относительно которых записаны уравнения состояния) любых других переменных.
Первое требование удовлетворяется специальной методикой составления уравнений состояния, которая будет рассмотрена далее.
Для выполнения второго требования в качестве переменных состояния следует принять потокосцепления (токи в ветвях с индуктивными элементами) и заряды (напряжения) на конденсаторах. Действительно, зная закон изменения этих переменных во времени их всегда можно заменить источниками ЭДС и тока с известными параметрами. Остальная цепь оказывается резистивной, а следовательно, всегда рассчитывается при известных параметрах источников. Кроме того, начальные значения этих переменных относятся к независимым, т.е. в общем случае рассчитываются проще других.
При расчете методом переменных состояния, кроме самих уравнений состояния, связывающих первые производные 



Таким образом, полная система уравнений в матричной форме записи имеет вид
 ; ; | (2) |
 . . | (3) |
Здесь 







Начальные условия для уравнения (2) задаются вектором начальных значений 
В качестве примера составления уравнений состояния рассмотрим цепь на рис. 4,а, в которой требуется определить токи 

По законам Кирхгофа для данной цепи запишем
 ; ; | (4) |
 ; ; | (5) |
 . . | (6) |
Поскольку 
или в матричной форме записи
Матричное уравнение вида (3) вытекает из соотношений (4) и (6):
Вектор начальных значений 

Непосредственное использование законов Кирхгофа при составлении уравнений состояния для сложных цепей может оказаться затруднительным. В этой связи используют специальную методику упорядоченного составления уравнений состояния.
Методика составления уравнений состояния
Эта методика включает в себя следующие основные этапы:
1. Составляется ориентированный граф схемы (см. рис. 4,б), на котором выделяется дерево, охватывающее все конденсаторы и источники напряжения (ЭДС). Резисторы включаются в дерево по необходимости: для охвата деревом всех узлов. В ветви связи включаются катушки индуктивности, источники тока и оставшиеся резисторы.
2. Осуществляется нумерация ветвей графа (и элементов в схеме), проводимая в следующей последовательности: первыми нумеруются участки графа (схемы) с конденсаторами, затем резисторами, включенными в дерево, следующими нумеруются ветви связи с резисторами и, наконец, ветви с индуктивными элементами (см. рис. 4,б).
3. Составляется таблица, описывающая соединение элементов в цепи. В первой строке таблицы (см. табл. 1) перечисляются емкостные и резистивные элементы дерева, а также источники напряжения (ЭДС). В первом столбце перечисляются резистивные и индуктивные элементы ветвей связи, а также источники тока.
Интеграл дюамеля и уравнение свертки записывается в виде


20.2. ВРЕМЕННОЙ МЕТОД РАСЧЕТА ПЕРЕХОДНЫХ ПРОЦЕССОВ. ИНТЕГРАЛ СВЕРТКИ. ИНТЕГРАЛ ДЮАМЕЛЯ
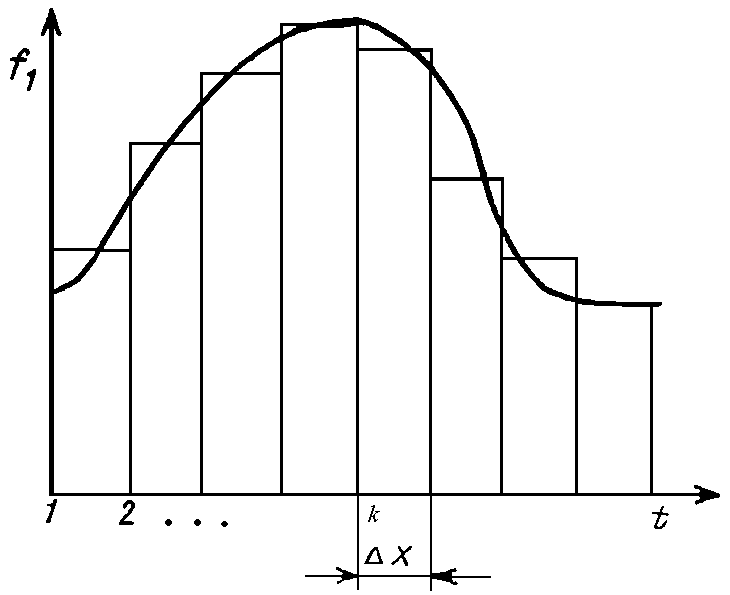
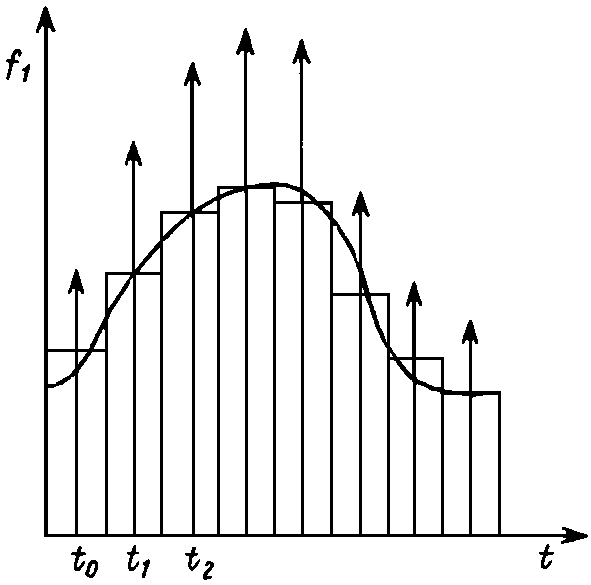
Рассмотрим процесс в цепи при действии на ее входе сигнала произвольной формы f 1 ( t ) (рис. 20.3). Этот сигнал можно представить в виде последовательности прямоугольных импульсов длительностью D x с амплитудами f 1 ( k D x ).
При малых значениях D x каждый такой импульс эквивалентен действию на цепь d -импульса, включаемого в момент t = k D x и имеющего площадь f 1 ( k D x ) D x . Поэтому входной сигнал представим в виде суммы 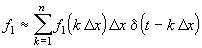
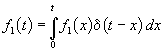
Поскольку реакция цепи на каждый d -импульс описывается импульсной характеристикой h d , то для выходной величины f 2 ( t ) можно записать аналогичный интеграл, в котором реакция на входной импульс d ( t – x ) выражена как h d ( t – x ):
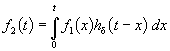
Полученный интеграл называется интегралом свертки и используется при вычислении реакции цепи f 2 ( t ) на воздействие f 1 ( t ) произвольной формы. Он и является основой временнóго метода расчета переходных процессов.
Как уже отмечалось, указанные выше пределы интегрирования требуют уточнения, особенно, при наличии в подынтегральных сомножителях слагаемых в виде d -функций. При вычислении интеграла свертки необходимо учитывать, что первый сомножитель под интегралом f 1 ( x ) = 0 при x h d ( t – x ) = 0 при t – x x > t + 0. Именно эти значения пределов интегрирования (– 0 x t f 1 d -слагаемое может содержаться в h d ( t – x ). Вклад этого слагаемого можно учесть отдельно. Для этого запишем
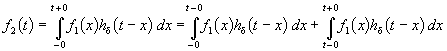
Так как второй интеграл можно преобразовать к виду 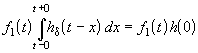
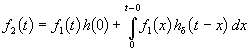
В последнем выражении под интегралом учитывается только ограниченная часть импульсной характеристики h d .
Пример использования интеграла свертки рассмотрен в Задаче 17.1.
Основные свойства интеграла свертки.
1. Поскольку при t f 1 ( t ) и h d ( t ) º 0, то пределы в интеграле свертки можно взять от — ¥ до ¥ , то есть
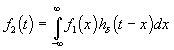
так как на добавленных отрезках (– ¥ , 0) и ( t , ¥ ) один из подынтегральных сомножителей тождественно равен нулю.
2. Переменные интегрирования можно заменять, используя связь t – x = y . Интеграл при этом примет вид
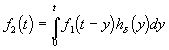
Операция свертки растягивает импульсный сигнал во времени. Пусть прямоугольный импульс A длительностью T (рис. 20.4, а ) действует на входе цепи, импульсная характеристика которой изображена на рис. 20.4, б . Такая цепь представляет интегратор с конечным временем интегрирования t .
В этом простом случае результат свертки легко найти графически. Пусть для определенности T > t , тогда для различных моментов времени t 1 , t 2 и t 3 произведение f 1 на h ( t – x ) будет определяться площадью перекрывающихся прямоугольников (рис. 20.4, в ), и выходной сигнал будет иметь вид, показанный на рис. 20.4, г . Таким образом, цепь суммирует длительность импульса T и собственное время t .
Интеграл Дюамеля. Интеграл свертки можно выразить через переходную характеристику. Это приводит к интегралу Дюамеля. Для его получения используем записанную п. 20.1 связь h d = dh / dt , из которой произведение h d ( t – x ) dx можно представить как – dh ( t – x ):
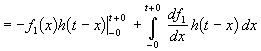
В последнем преобразовании использована формула интегрирования по частям. Так как внеинтегральный член равен нулю, то окончательно получим
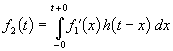
где 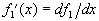
Неудобство этого выражения связано с d -слагаемыми в 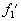
Последнее выражение является наиболее распространенной формой записи интеграла Дюамеля.
Если входная функция f 1 имеет разрывы, то для расчета переходного процесса временным методом удобнее использовать интеграл свертки, если она непрерывна, то интеграл Дюамеля (при неограниченной характеристике h d ).
При выполнении расчетов временным методом следует обращать внимание на: 1) различное аналитическое описание функции f 1 на различных отрезках у импульсов сложной формы; 2) правильный учет неограниченного характера функции h d (при вычислении интегралов с d- слагаемыми); 3) правильный учет разрывов функции f 1 в интеграле Дюамеля.
Пример расчета переходного процесса с помощью интеграла Дюамеля рассмотрен в Задачe 17.2.
Особенности применения операторного метода при определении «последействия» импульса. Реакция цепи на одиночный импульс длительностью Т при t > Т содержит лишь свободные составляющие процесса, соответствующие корням характеристического уравнения цепи. В связи с этим при использовании операторного метода нахождение оригинала по теореме разложения требует учета не всех корней знаменателя изображения реакции, а лишь тех из них, которые являются корнями знаменателя передаточной функции. Это существенно упрощает расчет, особенно для импульсов сложной формы. Пусть определено изображение импульса с конечной длительностью
(f1(t) = 0 при t > T). При воздействии такого импульса на цепь с передаточной функцией K( s) = Q(s)/P(s) реакция при t > Т содержит лишь экспоненты е s k t с показателями, в которые входят корни P(s) =0. Поэтому для реакции при t > Т по теореме разложения имеем
(предполагается отсутствие кратных корней s k) .
Рассмотрим в качестве примера Задачу 17.1. Передаточная функция цепи имеет выражение K( s) = s t /(l + s t ). Операторное изображение входного сигнала имеет вид
Поэтому изображение выходного напряжения равно
что совпадает с результатом, полученным в Задаче 17.1.
Если воздействующий импульс f1(t) не имеет простого аналитического описания, то его представляют в виде совокупности импульсов прямоугольной формы с амплитудой f1(tk) длительностью D tk, каждый из которых рассматривается как d -импульс
С помощью теоремы запаздывания получим изображение входного сигнала F1(s)
При таком представлении временной метод приводит к замене интеграла свертки суммой; для выходного сигнала будем иметь
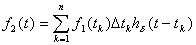
Анализ переходных и установившихся процессов методом интеграла свертки
Содержание:
Анализ переходных и установившихся процессов методом интеграла свертки:
Интеграл Дюамеля применяют для расчета токов, напряжений переходных режимов в схеме с нулевыми начальными условиями, если воздействие имеет сложную форму. В табл. 7.1 приведены формы записи интеграла Дюамеля.
При определении тока или напряжения переходного режима, обозначенных 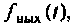
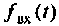
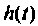
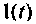
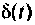
Временные характеристики бывают переходные 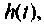
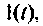
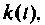
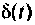
Из выражения (7.9) следует, что переходная характеристика равна току 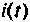
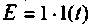
Импульсная характеристика 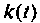
В табл. 7.2 приведены графики типовых воздействий и разновидностей временных характеристик.
Методы определения переходных и импульсных характеристик
Классический метод построения переходных и импульсных характеристик:
Для расчета переходных характеристик классическим методом:
- на вход цепи полают единичное ступенчатое воздействие напряжения (тока)
- записывают формулу для определения h(t) используя соотношение
- находят классическим методом
т.е. ток или напряжение переходного режима в зависимости от разновидности определяемой характеристики;
- рассчитывают
и строят график;
- проверяют расчет для
по схеме и сравнивают с аналитическим выражением
Для расчета импульсных характеристик пользуются соотношением (7.10), связывающим переходные и импульсные характеристики
Пример расчета переходных и импульсных характеристик классическим методом
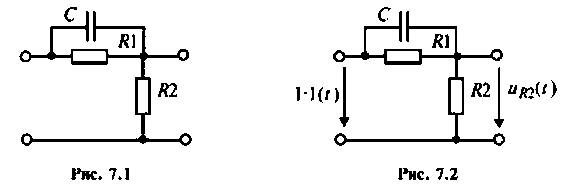
Для дифференцирующего RС-контура (рис. 7.1) определить переходную и импульсную характеристики по напряжению на сопротивлении R2.
На вход цепи, изображенной на рис.7.2. подают единичное ступенчатое напряжение
Записывают формулу для определения h(t), используя соотношение (7.9) и табл. 7.2
Определяют классическим методом напряжение переходного режима на сопротивлении R2:
Начальное значение А определяют по выражению
Корен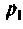
Напряжение переходного режима на сопротивлении 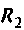
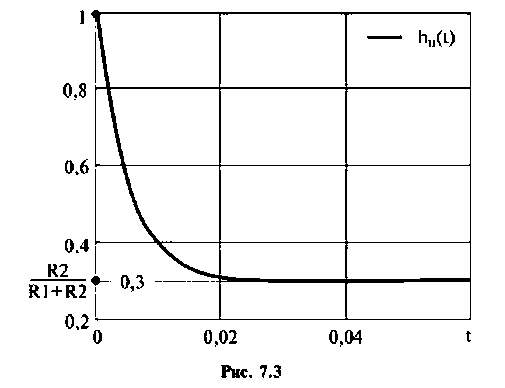
Определяют переходную характеристику по напряжению
График переходной характеристики по напряжению 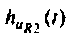
Определяют импульсную характеристику по связи (7.10) с переходной
Размерность импульсной характеристики (1/с), а физически характеризует скорость изменения переходной характеристики.
Построение переходных и импульсных характеристик операторным методом
Для расчета переходных и импульсных характеристик операторным методом:
1)для заданной электрической цени и операторной форме составляют уравнения входа и выхода, например для 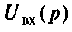
2) определяют выражение для передаточной функции электрической цепи
3) определяют с помощью обратного преобразования Лапласа импульсную характеристику
4) получают изображение переходной характеристики по полученной передаточной функции
5) определяют переходную характеристику по полученному изображению переходной функции с помощью обратного преобразования Лапласа
Пример расчета переходных и импульсных характеристик операторным методом. Для дифференцирующего RС-контура (см. рис.7.1) определить переходную и импульсную характеристики по напряжению на сопротивлении
Для определения передаточной функции контура составим уравнения напряжения этого контура в операционной форме
Из второго уравнения находим 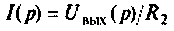
откуда передаточная функция контура
где 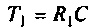
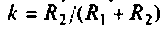
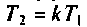
Из формулы (7.15) можно определить изображение переходной функции контура 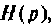
Методы определения импульсной (7.12) и переходной характеристик (7.14) электрических цепей и систем автоматического управления с помощью обратного преобразования хорошо известны и широко применяются в инженерной практике [4, 6, 14], поэтому не будем на них подробно останавливаться, а получим временные характеристики с помощью программной среды Mathcad.
Применим стандартную функцию invlaplace в среде Mathcad.
Импульсная характеристика 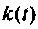
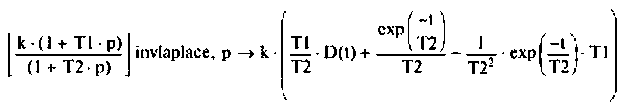
Переходная характеристика h(t) — по выражению
Порядок расчета переходных процессов методом интеграла Дюамеля
- Записывают одну из восьми форм интеграла Дюамеля, приведенных и табл. 7.1.
- Определяют соответствующую временную характеристику.
- Вычисляют компоненты, входящие в интеграл Дюамеля.
- Производят интегрирование и находят искомую функцию.
- Проверяют расчет для
строят график найденной характеристики.
Для построения выходных переменных воспользуемся интегралом свертки в форме записи (7.6) и средой Mathcad:
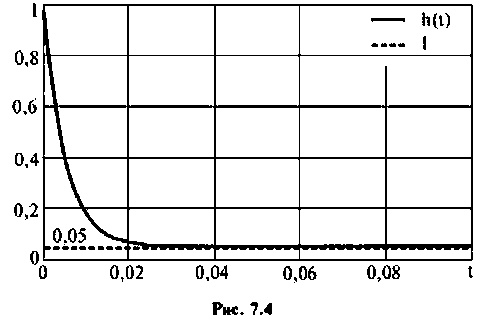
- выходная (переходная) функция электрической цепи приведена на рис. 7.4;
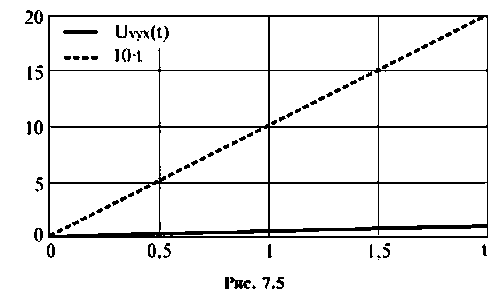
- реакция электрической цепи на линейное воздействие
показана на рис. 7.5.
По виду входной и выходной величин осуществляется оценка свойств электрической цепи, исследуется влияние изменения параметров цепи на характер процессов, протекающих в ней.
Примеры решения задач
Пример 7.4.1.
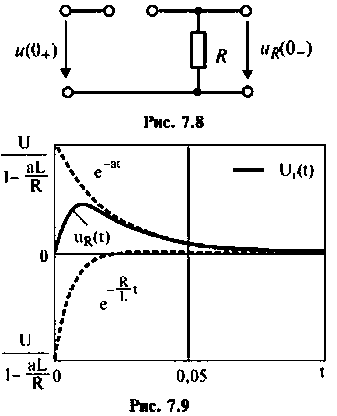
Определить напряжение на сопротивлении R интегрирующей RL-цепи (рис. 7.6). если напряжение на входе
Решение
Выбирают аналитическое выражение интеграла Дюамеля из табл. 7.1
Конкретизируя величины, входящие в интеграл Дюамеля, получают
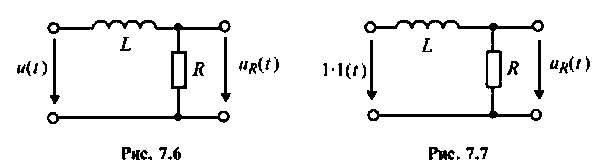
Определяют переходную характеристику но напряжению на сопротивлении R как
На рис. 7.7 приведена схема для расчета переходной характеристики 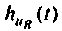
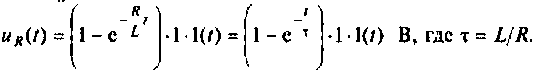
Следовательно,
Вычисляют компоненты, входящие в интеграл Дюамеля:
Производя интегрирование в соответствии с выражением (7.10), находят искомое напряжение
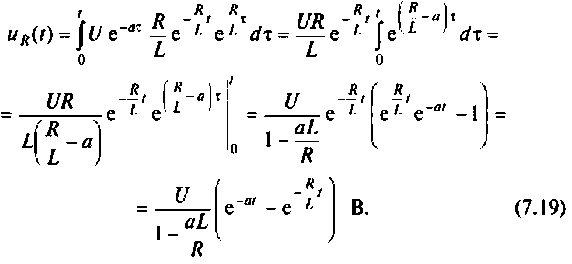
Проверяют расчет для
На рис. 7.К приведена эквивалентная схема для 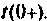
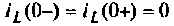
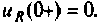
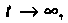
Подставляя 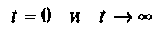
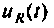
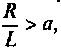
Пример 7.4.2.
Определить напряжение на сопротивлении R и интегрирующей /fi-цеии (рис. 7.7), если напряжение па входе 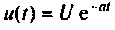
Дано:
Решение
Определение напряжения 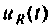
В этом выражении составляющая 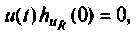
Определим подынтегральную функцию, для этого воспользуемся выражениями 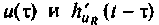
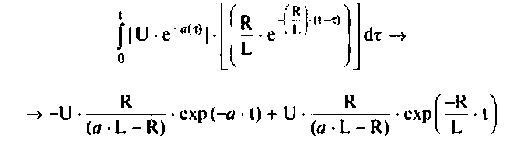
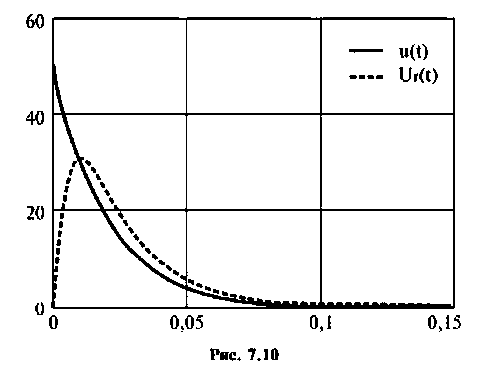
Программа для вычисления и построения входного и выходного напряжения имеет следующий вид
Графическое изображение входного и выходного напряжений показано на рис. 7.10.
Пример 7.4.3.
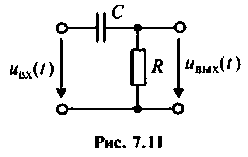
Для повышения разрешающей способности PЛC применяют дифференцирование сигналов. Рассчитать напряжение на выходе RС-цепи, поступающее на вход преобразовательного устройства РЛС, если на входе цепи (рис. 7.11) появляется прямоугольный видеоимпульс с параметрами 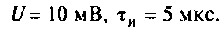
Решение
Определяют переходную характеристику по напряжению
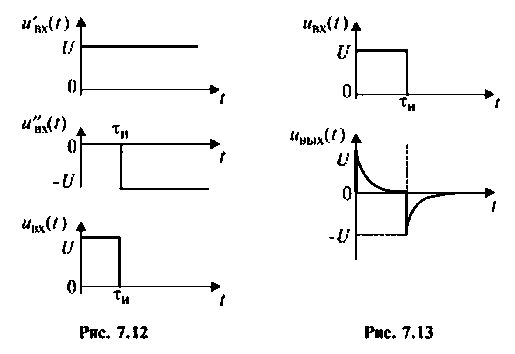
Входной и выходной сигналы методом наложения представляют в виде суммы ступенчатых воздействий (рис. 7.12). Входной сигнал определяют из соотношения
Приближенно графики входного и выходного напряжений изображены на рис. 7.13.
В математической среде Mathcad решение этой задачи упрощается и может быть представлено следующими программами:
1) для моделирования входного импульсного напряжения
2) для моделирования выходного напряжения
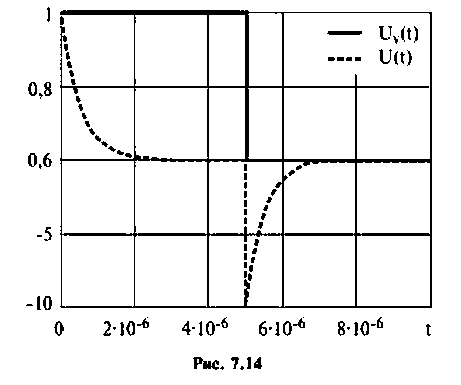
Графики напряжений приведены па рис. 7.14.
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Операторный метод расчета переходных процессов
- Метод пространства состояний электрических цепей
- Синтез электрических цепей
- Цепи с распределенными параметрами
- Переходные процессы в электрических цепях с сосредоточенными параметрами
- Переходные процессы в колебательных контурах
- Расчет переходных процессов
- Классический метод расчета переходных процессов
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
http://eelib.narod.ru/toe/Novg_2.01/20/Ct20-2.htm
http://www.evkova.org/analiz-perehodnyih-i-ustanovivshihsya-protsessov-metodom-integrala-svertki

 (или
(или  ) для исследуемой цепи.
) для исследуемой цепи. (или
(или  ) путем формальной замены t на
) путем формальной замены t на  .
. .
.





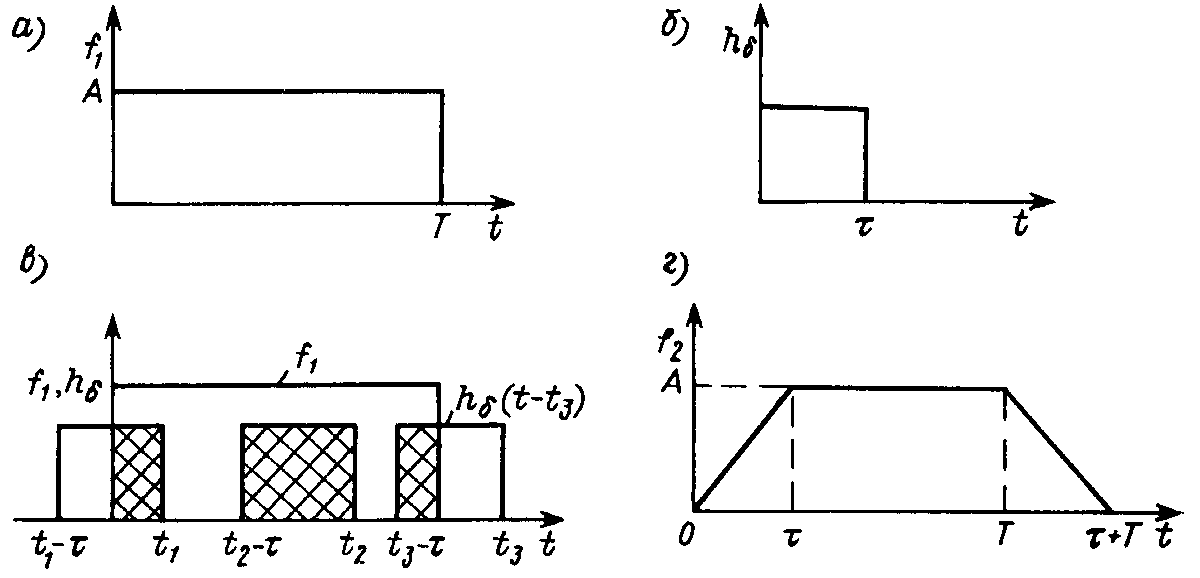
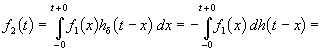
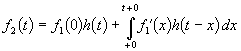
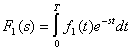
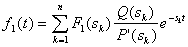
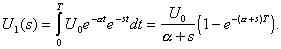
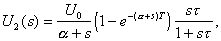
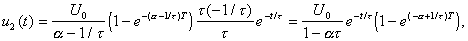
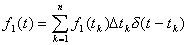
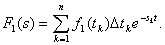


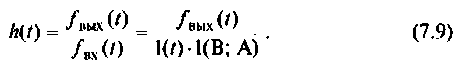
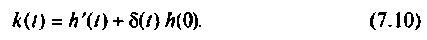
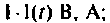
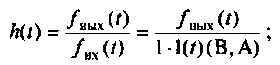
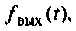 т.е. ток или напряжение переходного режима в зависимости от разновидности определяемой характеристики;
т.е. ток или напряжение переходного режима в зависимости от разновидности определяемой характеристики;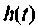 и строят график;
и строят график;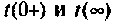 по схеме и сравнивают с аналитическим выражением
по схеме и сравнивают с аналитическим выражением 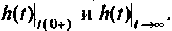
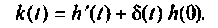
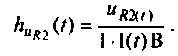
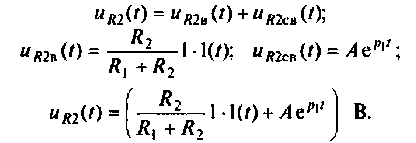
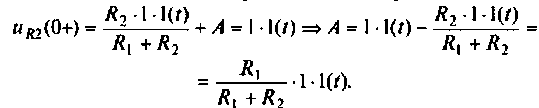
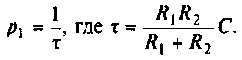
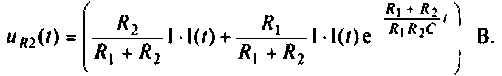
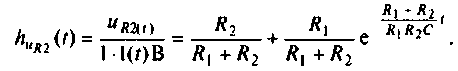
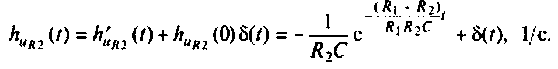
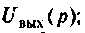




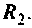
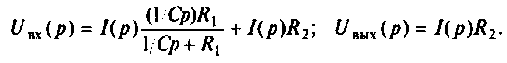
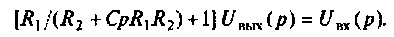
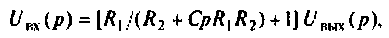
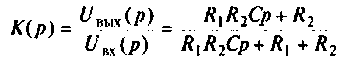
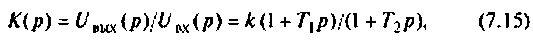
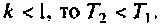
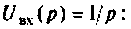
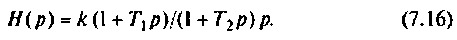
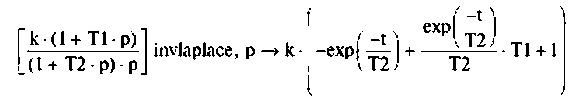
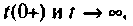 строят график найденной характеристики.
строят график найденной характеристики.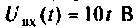 показана на рис. 7.5.
показана на рис. 7.5.