Интегральное уравнение 2 го рода
Последние действия на сайте
Интегральное уравнение
Материал из Википедии — свободной энциклопедии
Интегра́льное уравне́ние — функциональное уравнение, содержащее интегральное преобразование над неизвестной функцией. Если интегральное уравнение содержит также производные от неизвестной функции, то говорят об интегро-дифференциальном уравнении.
Классификация интегральных уравнений
Линейные интегральные уравнения
Это интегральные уравнения, в которые неизвестная функция входит линейно:
где 


Уравнения Фредгольма
Уравнения Фредгольма 2-го рода
Уравнения Фредгольма 2-го рода — это уравнения вида:
Пределы интегрирования могут быть как конечными, так и бесконечными. Переменные удовлетворяют неравенству: 

Ядра, удовлетворяющие последнему условию, называют фредгольмовыми. Если 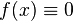
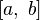
Уравнения Фредгольма 1-го рода
Уравнения Фредгольма 1-го рода выглядят также, как и уравнение Фредгольма 2-го рода, только в них отсутствует часть, содержащая неизвестную функцию вне интеграла:
при этом ядро и свободный член удовлетворяют условиям, сформулированным для уравнений Фредгольма 2-го рода.
Уравнения Вольтерра
Уравнения Вольтерра 2-го рода
Уравнения Вольтерра отличаются от уравнений Фредгольма тем, что один из пределов интегрирования в них является переменным:
Уравнения Вольтерра 1-го рода
Также, как и для уравнений Фредгольма, в уравнениях Вольтерра 1-го рода отсутствует неизвестная функция вне интеграла:
В принципе, уравнения Вольтерра можно рассматривать как частный случай уравнений Фредгольма, если переопределить ядро:
Однако некоторые свойства уравнений Вольтерра не могут быть применены к уравнениям Фредгольма.
Нелинейные уравнения
Можно придумать немыслимое многообразие нелинейных уравнений, поэтому дать им полную классификацию не представляется возможным. Вот лишь их некоторые типы, имеющие большое теоретическое и прикладное значение.
Уравнения Урысона
Постоянная M — это некоторое положительное число, которое заранее не всегда может быть определено.
Уравнения Гаммерштейна
Уравнения Гаммерштейна являются важным частным случаем уравнения Урысона:
где 
Уравнения Ляпунова — Лихтенштейна
Именами Ляпунова — Лихтенштейна принято называть уравнения, содержащие существенно нелинейные операторы, например, уравнение вида:
Нелинейное уравнение Вольтерра
где функция 
Методы решения
Прежде, чем рассмотреть некоторые методы решения интегральных уравнений, следует заметить, что для них, как и для дифференциальных уравнений не всегда удается получить точное аналитическое решение. Выбор метода решения зависит от вида уравнения. Здесь будут рассмотрены несколько методов для решения линейных интегральных уравнений.
Преобразование Лапласа
Метод преобразования Лапласа может быть применён к интегральному уравнению, если входящий в него интеграл имеет вид свёртки двух функций:
то есть, когда ядро является функцией разности двух переменных:
Например, дано такое уравнение:
Применим преобразование Лапласа к обеим частям уравнения:

Применяя обратное преобразование Лапласа, получим:
Метод последовательных приближений
Метод последовательных приближений применяется для уравнений Фредгольма 2-го рода, если выполняется условие:
Это условие необходимо для сходимости ряда Лиувилля — Неймана:
который и является решением уравнения. (K k f)(x) — k -ая степень интегрального оператора (Kf)(x) :
Впрочем, такое решение является хорошим приближением лишь при достаточно малых | λ | .
Метод резольвент
Метод резольвент является не самым быстрым решением интегрального уравнения Фредгольма второго рода, однако иногда нельзя указать других путей решения задачи.
Если ввести следующие обозначения:
то повторными ядрами ядра 
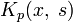
Ряд, составленный из повторных ядер,
называется резольвентой ядра 


Например, для интегрального уравнения
повторными будут следующие ядра:
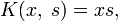
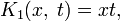

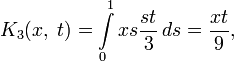
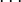
а резольвентой — функция
Тогда решение уравнения находится по формуле:
Метод сведения к алгебраическому уравнению
В случае, если ядро интегрального уравнения Фредгольма является вырожденным, то есть 
где 
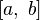
где 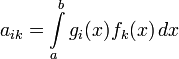

Приложения
Термин «интегральное уравнение» ввёл в 1888 году Дюбуа-Реймон, однако первые задачи с интегральными уравнениями решались и ранее. Например, в 1811 году Фурье решил задачу об обращении интеграла, которая теперь носит его имя.
Формула обращения Фурье
Задача состоит в нахождении неизвестной функции f(y) по известной функции g(x) :
Фурье получил выражение для функции f(y) :
Сведение задачи Коши к интегральному уравнению
К нелинейным интегральным уравнениям Вольтерра приводит задача Коши для обыкновенных дифференциальных уравнений:
В самом деле, это уравнение можно проинтегрировать по t от a до t :
Решение начальной задачи для линейных дифференциальных уравнений приводит к линейным интегральным уравнениям Вольтерра 2-го рода. Этим еще в 1837 году воспользовался Лиувилль. Пусть, например, поставлена задача:
Для уравнения с постоянными коэффициентами с теми же начальными условиями:
решение может быть найдено методом вариации постоянных и представлено в виде:
Тогда для исходного уравнения получается:
— интегральное уравнение Вольтерра 2-го рода.
a,» src=»http://upload.wikimedia.org/math/3/c/c/3cca9038417f8968682c783191e3f6c7.png» />
также может быть сведено к интегральному уравнению Вольтерра 2-го рода.
Задача Абеля
Исторически считается, что первой задачей, которая привела к необходимости рассмотрения интегральных уравнений, является задача Абеля. В 1823 году Абель, занимаясь обобщением задачи о таутохроне, пришёл к уравнению:
где f(x) — заданная функция, а 
У Абеля формулировка задачи выглядела примерно так:
Материальная точка под действием силы тяжести движется в вертикальной плоскости
по некоторой кривой. Требуется определить эту кривую так, чтобы материальная точка, начав свое движение без начальной скорости в точке кривой с ординатой x , достигла оси Oξ за время t = f1(x) , где f1(x) — заданная функция.
Если обозначить угол между касательной к траектории и осью Oξ как β и применить законы Ньютона, можно прийти к следующему уравнению:
Решения интегральных уравнений онлайн
В этом разделе мы рассмотрим типовые задачи по интегральным уравнениям с решениями. Интегральное уравнение содержит неизвестную функцию под знаком интеграла (по аналогии как дифференциальное — функцию под знаком дифференциала:)).
Выделяют два основных класса интегральных уравнений: уравнения Фредгольма I и II рода:
$$ (I) \quad \int_a^b K(x,s)u(s)ds = f(x),\\ (II) \quad u(x)=\int_a^b K(x,s)u(s)ds + f(x). $$
В случае переменного верхнего предела интегрирования получаем соответственно уравнение Вольтерра I и II рода:
$$ (I) \quad \int_a^x K(x,s)u(s)ds = f(x),\\ (II) \quad u(x)=\int_a^x K(x,s)u(s)ds + f(x). $$
Это линейные неоднородные уравнения (при $f(x)=0$ — однородные), иногда рассматриваются более общий случай с параметром $\lambda$ перед интегралом.
Ниже вы найдете примеры нахождения решений интегральных уравнений, собственных значений и функций, исследования ядра, применения интегральных уравнений для решения других задач.
Примеры решений интегральных уравнений
Задача 1. Пользуясь теоремой Гильберта-Шмидта, исследовать и решить интегральное уравнение 2-го рода $(E+\lambda A)x=y$ в гильбертовом пространстве $X$.
Задача 2. Найти собственные значения и собственные функции уравнения:
$$ y(x)=\lambda \int_0^1 (\cos 2\pi x +2x \sin 2\pi t +t \sin \pi x)y(t)dt. $$
Задача 3. Решить уравнение Вольтерры, сведя его к обыкновенному дифференциальному уравнению.
Задача 4. Решить или установить неразрешимость уравнений с вырожденным ядром.
Задача 5. Решить интегральное уравнение, сведя его предварительно к обыкновенному дифференциальному уравнению.
Задача 6. Найти резольвенту для интегрального уравнения Вольтерры со следующим ядром $K(x,t)=x^<1/3>t^<2/3>$.
Задача 7. Исследовать решения уравнения с вырожденным ядром при различных значениях параметра $\lambda$ (ограничиться случаем вещественных характеристических чисел).
$$ y(x)-\lambda \int_0^1 x y(t)dt = \sin 2\pi x. $$
Задача 8. Для симметричного ядра $$K(x,t) = \frac<1> <2>\sin |x-t| \quad (0 \le, x,t \le \pi)$$ найти характеристические числа и соответствующие им собственные функции, сводя интегральное уравнение к однородной краевой задаче для обыкновенного дифференциального уравнения.
Задача 9. Решить краевую задачу, используя функцию Грина
Задача 10. Применяя преобразование Лапласа, решить интегральное уравнение
Помощь с интегральными уравнениями
Если вам нужна помощь с решением задач и контрольных по интегральным уравнениям (и другим разделам математического и функционального анализа), обращайтесь в МатБюро. Стоимость подробной консультации от 200 рублей , оформление производится в Word, срок от 1 дня.
ЛИНЕЙНЫЕ ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ ФРЕДГОЛЬМА ВТОРОГО РОДА В ПРИЛОЖЕНИЯХ К ЭКОНОМИКЕ Текст научной статьи по специальности « Математика»
Аннотация научной статьи по математике, автор научной работы — Паршикова Г.Ю., Перфильев А.А., Силаев А.А.
В условиях пандемии экономика вступила в длительную фазу, характеризуемую тем, что стратегические решения приходится принимать в условиях неточной, а порой и преднамеренно искажаемой конкурентами информации, причем потоки этой информации то дискретны, то непрерывны. С математической точки зрения подобные явления означают: исследователь переходит от конечных сумм и функциональных рядов к построению и решению интегральных уравнений с параметром, являющимся либо управляемой, либо случайной величиной. С задачей определения и изучения свойств решений системы экономической динамики с неизвестным параметром исследователь сталкивается в моделях экологии, непрерывно текущих химических процессов, нефтепереработки и нефтеочистки, теории катастроф. В статье рассматриваются интегральные уравнения Фредгольма второго рода c различными вырожденными ядрами и различными внешними воздействиями. При этом авторов интересуют как точные, так и приближенные решения, для получения которых авторы используют метод малого параметра.
Похожие темы научных работ по математике , автор научной работы — Паршикова Г.Ю., Перфильев А.А., Силаев А.А.
FREDHOLM LINEAR INTEGRAL EQUATIONS OF THE SECOND KIND IN APPLICATIONS TO ECONOMICS
In the context of the pandemic, the economy has entered a long phase characterized by the fact that strategic (financial) decisions have to be made in conditions of inaccurate, missing, and sometimes deliberately distorted information by competitors, and the flow of this information is either discrete or continuous. From a mathematical point of view, such phenomena mean that the researcher moves from finite sums and functional series to the construction and solution of integral equations with a parameter that is either a controlled or random variable. The problem of determining and studying the properties of solutions to a system of economic dynamics with an unknown parameter is faced by researchers in models of ecology, continuously running chemical processes, oil refining and refining, and disaster theory Most processes with cumulative nature, where the resulting indicator continuously accumulates or continuously «evaporates», allows mathematical modeling using the apparatus of integral equations. The researcher meets the problem of determining and studying properties of solutions to a system of economic dynamics with an unknown parameter in models of ecology, continuously chemical processes, and oil refining. The article deals with Fredholm integral equations of the second kind with various degenerate kernels and various external influences. The authors are interested in both exact and approximate solutions that use the method of small parameter to get them.
Текст научной работы на тему «ЛИНЕЙНЫЕ ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ ФРЕДГОЛЬМА ВТОРОГО РОДА В ПРИЛОЖЕНИЯХ К ЭКОНОМИКЕ»
Линейные интегральные уравнения Фредгольма второго рода в приложениях к экономике
Не можете найти то, что вам нужно? Попробуйте сервис подбора литературы.
^ С = 2е(2е 5) — единственное решение.
Таким образом, функция при Л Ф Л функция
у = x + Á-ex — C = x + С
y(x) = x + Á — j cos(x +1)y(t)dt,
или, упрощая по формуле «косинуса суммы»,
y (x) = x + Á- cos x — j cos t — y(t )dt — sin x — j sin t — y(t )dt _ о 0
Обозначая неизвестные числа через:
jy(t)costdt = a; jy(t)sintdt = p, (10)
получаем формулу для решения y (x) = x + Á- (a cos x — p sin x). (11)
Тогда подставляя функцию y (t) = t + Á — (a cos t — p — sin t). в формулы (10), получаем два линейных неоднородных алгебраических уравнения с тремя неизвестными параметрами:
a = Х-a-j cos2 tdt -Х- p-j cos t — sin tdt + j t cos tdt,
P = Х-a-j cos t -sin tdt -Х- p-j sin2 tdt + j t sin tdt. 0 0 0 Вычислив интегралы
j sin t- cos tdt = 0; j t- sin tdt = л; j t — cos tdt = -2;
j sin2 tdt =j cos2 tdt
2е2 -Л(е2 -1) есть точное (аналитическое) решение интегрального уравнения (7).
Заметим, что собственное число Л = Л =-не
зависит от вида правой части (1) и (7), а зависит только от ядра. Поэтому оно и называется собственным значением ядра (интегрального уравнения).
Интегральное уравнение, описывающее периодический процесс (например, функционирование транспортных систем с их отдельными графиками работы в будние и выходные дни, либо математические модели утилизации бытовых отходов с их квази-периодичностью эффекта насыщения, или квази-периодически повторяющиеся катастрофы — например, извержение вулкана Этны в Сицилии), приобретает вид
исследуем линейную систему двух алгебраических уравнений с тремя неизвестными:
Случай 1. Если Х = —, то a Ек п
система (13) решений не имеет.
Случай 2 Если х = — — , то p
не имеет решений.
Примечание: х = + — являются собственными зна-
чениями однородного интегрального уравнения, которое, в этих двух случаях, согласно формуле
y0 (x) = Х- (a cos x — p sin x)
имеет бесконечную систему собственных функций:
1) при х = Х=— ^ y01)(x) = — a -cos x Va* 0;
2) при á = á =— ^y02)(x) =—p-sinx vp*0.
Очевидно, что система ненулевых функций
Рассмотрим важный в экономике (например, в транспортных системах, причем как для грузового, так и для легкового видов транспорта, а также при исследовании
турбулентности океанических течений) случай, при котором Х е (-да; — —) и (-—;—) и (—; +да) . Тогда си-
ж ж ж ж стема двух линейных уравнений с тремя неизвестными параметрами имеет решение, сводящееся к одному параметру Х, принадлежащих указанному множеству: 2 4
а • (Л ж -1) = 2ж + 2, 2
Отсюда получаем: 2
1) если Л = —, то а ei ж
стема (17) решений не имеет.
и, следовательно, си-
2) если Л = — — , то ß
и система (17) не
3) если л ф + —, то существует решение системы ж
ж ■ Л — 2 2(ж2 +ж-12) ж ■ Л+ 2
и существует, следовательно, единственное аналитическое решение интегрального уравнения (16)
и, согласно формуле (11), получаем единственное аналитическое решение у(х;Х) = у(х) вида 4Х
, , 4ж + 4 24 — 2ж2 — 2ж . +ЛА—cos x +—sin x
Например, при Х = 0 имеем y(х;0) = X — непериодическое решение.
Решение вида (15) при Х Ф 0 мы называем квазипериодическим решением, если при этом хф+— (не сов-
падает с собственным числом). Наименьший «квази-пе-риод» в этом случае — положительный и равен 27 .
(при Х е (-«; -l) и (—;0) и (0;-) и (-; +ю)).
Рассмотрим теперь интегральное уравнение с тем же периодическим ядром, но другим усиленным внешним воздействием:
y (х) = X2 + x + 5 + Х- J cos( x +1) y(t) dt (16)
Вводим неизвестные по формулам (10) и перепишем уравнение (16) в виде:
y (t) = t2 +1 + 5 + Х- (a- cos t — p- sin t)
Система, аналогичная (12), имеет вид:
a = J t2 cos tdt + J t cos tdt + 5J cos tdt + a Х •77,
p = j t2 — sin tdt + J t — sin tdt + 5 J sin tdt — ft- Х •—. 0 0 0 2 Вычисляя интегралы, получим систему:
В заключении рассмотрим интегральное уравнение Фредгольма второго рода с вырожденным ядром, с точностью до постоянной, являющимся плотностью двумерного нормального распределения с нулевым математическим ожиданием и дисперсией, равной 1/2
K (x, y) = K ( y, x) = e-( x2+y2) (19)
на бесконечном промежутке интегрирования.
xdx^ j e»ydy = j j e»((+y’ )xdy = ,
то нормировочный множитель c = —— легко вно
сится в параметр Х, то есть в «будущее» собственное значение (однородного) интегрального уравнения. Исследуем интегральное уравнение
e (x2+s2)y(s)ds + x, (20)
причем правая часть (линейная функция) /(х) = х взята для того, чтобы посмотреть, каким образом неоднородность (простейшего вида) влияет на существование и/или единственность решения при переходе от однородного равнения к неоднородному.
Для уравнения (22) можно найти точное решение. Для этого преобразуем уравнение (не забывая при этом,
что мультипликативный параметр С =_ внесен в
«будущее» собственное значение однородного уравнения, то есть в параметр Х):
При любом ограниченном либо растущем не быст- являющаяся, однако, подпространством, поскольку рее, чем в% ■ х» ■ СОПЯг У» решении, несобствен- У = 0 являющаяся решением интегральн°г° уравне-
2 . (21**) У Л Е +да) , не может, в силу своей
интеграл первого рода | е-5 у(5является аб- тривиальности, являться собственной функцией /.
солютно сходящимся, если у(э) не имеет особенностей Случай 2. Пусть УЛ Ф . Тогда из линейного
второго рода у 5 е [0; +да) . Поэтому, обозначая, точ- 4п
нее вводя в уравнение новый неизвестный параметр алгебраического уравнения (21**) однозначно нахо-
+да 2 дится 1 . Подставляя найденное значение
приходим к линейному уравнению с двумя неизвест- р в формулу (23), находим аналитический вид решения ными параметрами
2 неоднородного уравнения (21)
у(х) = Лр■ е- + X. (23) Л л.Л
у(х) = ^-= ■е- + х = ^(х;Л), (25)
у(я) = Лр^ е* + 5, ^ 2^2 242 ч
подставим в уравнение (23), получим линейное урав- причем Л Е (-да;—т=-) и (—; +да) .
нение для нахождения неизвестного параметра Р:
Исследуем отдельно функцию
о о ________________________I п I — 2\/2
предположив, что Л Pn—1(s)ds
= е»х • ^-т. (29) 0 2 2 Теперь можем выписать в общем случае приближенное решение в виде степенного ряда (относительно параметра Х)
правым концом которого и является
«запретное» значение параметра Х при построения аналитического решения (27**). Этот правый конец и является единственным собственным значением однородного уравнения (21**), соответствующие собственные функции которого задаются формулой
Будем теперь искать решение того же интегрального уравнения методом малого параметра Х [4] в форме степенного ряда
Подставляя выражение (30) в интегральное уравнений (21) и приравнивая функции при одинаковых степенях Х, последовательно находим:
Рз (x) = j K(x, s) ■ (2 (s)ds = ■ j e»2? ds = e
Продолжая этот итерационный процесс, окончательно находим
Авторы убеждаются в полной идентичности формул (30) и (27**). Однако есть и принципиальная разница: ре-
шение (27**) справедливо УХ Ф 2 • — (то есть, за ис-
ключением собственного значения соответствующего однородного уравнения), тогда как формула (30) дает решение того же самого уравнения (21), но для компактного множества, именно для интервала
, где const отлична от нуля.
Экономические процессы, характеризуются как правило многовариантностью выбора, их модели имеют хотя бы одно собственное значение (см формулу (6*) и аналогичные ей), потому что согласно теореме Фредгольма, если параметр Я не является собственным значением, то однородное уравнение допускает лишь тривиальное решение. Напротив, если экономический процесс эмпирически однозначен и однороден, то есть при
f ( x) = 0 (или на практике близких к нулевому значению) имеет только тривиальное решение, причем для любой непрерывно возмущающей функции f(x) (ненулевое воздействие на систему) решение существует и единственно. Таким образом, априорный математический анализ системы позволяет определять многовариантные экономические стратегии и отличные от однова-риантных — путем анализа однородных уравнений Фредгольма (нахождение их собственных значений и собственных функций). Рассматриваемые модели допускают вариацию возмущающего воздействия (правой части уравнения Фредгольма). Например, для любой произвольной квадратичной функции соответствующее решение неоднородного интегрального уравнения будет точным (при условии, что однородное уравнение имеет точное решение). Однако, при Af > 0 встает вопрос: устойчива или нет исследуемая система относительно вариации возмущающего воздействия. Последнее обстоятельство приобретает особую важность в случае построения теории экологических катастроф.
1. Краснов, М.А. Интегральные уравнения. Учебное пособие/М.А. Краснов, Л.И. Киселев, Г.И. Макаренко. -М.: Книжный дом «Либроком», 2012,192 с.
2. Интегральные уравнения. Часть 1: справочник для вузов. /А.Д. Полянин, А.В. Манжиров. — 2-е изд., испр. и доп.- М.: Юрайт, 2017, 365 с.
3. Дифференциальные и интегральные уравнения: учебное пособие в 3-х частях/ сост. Кручек М.М., Све-това Н.Ю., Семенова Е.Е. — Петрозаводск: Изд-во ПетрГУ, 2014.
4. Корн, Г. / Г. Корн, Т. Корн. Справочник по математике для научных работников и инженеров. М.: Наука, 2007.
5. Арнольд, В.И. Теория катастроф. 14-е изд. стер. /В.И. Арнольд. М.: Изд-во Ленанд, 2020, 128 с.
Fredholm linear integral equations of the second kind in
applications to economics Parshikova G.Yu., Perfilyev A.A., Silaev A.A.
State University of management
In the context of the pandemic, the economy has entered a long
phase characterized by the fact that strategic (financial)
decisions have to be made in conditions of inaccurate, missing, and sometimes deliberately distorted information by competitors, and the flow of this information is either discrete or continuous. From a mathematical point of view, such phenomena mean that the researcher moves from finite sums and functional series to the construction and solution of integral equations with a parameter that is either a controlled or random variable. The problem of determining and studying the properties of solutions to a system of economic dynamics with an unknown parameter is faced by researchers in models of ecology, continuously running chemical processes, oil refining and refining, and disaster theory
Most processes with cumulative nature, where the resulting indicator continuously accumulates or continuously «evaporates», allows mathematical modeling using the apparatus of integral equations. The researcher meets the problem of determining and studying properties of solutions to a system of economic dynamics with an unknown parameter in models of ecology, continuously chemical processes, and oil refining.
The article deals with Fredholm integral equations of the second kind with various degenerate kernels and various external influences. The authors are interested in both exact and approximate solutions that use the method of small parameter to get them.
Keywords: Fredholm integral equation, degenerate kernel, eigenvalues equations, eigenfunctions
1. Krasnov, M.A. Integral equations. Textbook / M.A. Krasnov, L.I.
Kiselev, G.I. Makarenko. — M .: Book House «Librokom», 2012,192 p.
2. Integral equations. Part 1: a reference book for universities. /HELL. Polyanin, A.V. Manzhirov. — 2nd ed., Rev. and additional — M .: Yurayt, 2017, 365 p.
3. Differential and integral equations: a tutorial in 3 parts / comp.
Kruchek M.M., Svetova N.Yu., Semenova E.E. — Petrozavodsk: Publishing house of PetrSU, 2014.
4. Korn, G./G. Korn, T. Korn. A guide to mathematics for scientists
and engineers. Moscow: Nauka, 2007.
5. Arnold, V.I. Catastrophe theory. 14th ed. erased. /IN AND. Arnold. Moscow: Lenand Publishing House, 2020, 128 p.
Надоели баннеры? Вы всегда можете отключить рекламу.
http://www.matburo.ru/ex_ma.php?p1=maintur
http://cyberleninka.ru/article/n/lineynye-integralnye-uravneniya-fredgolma-vtorogo-roda-v-prilozheniyah-k-ekonomike



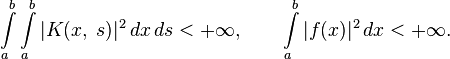
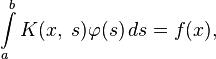
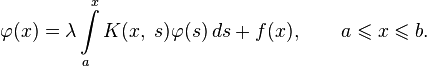
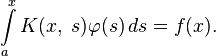

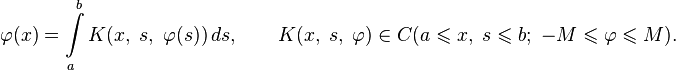

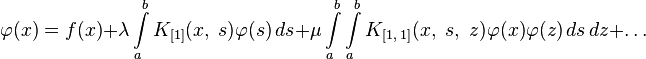

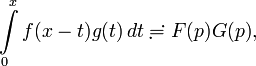
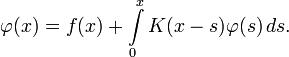

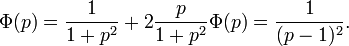
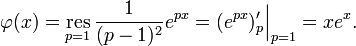


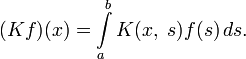
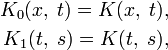





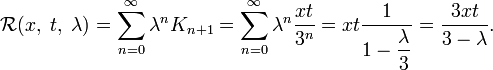


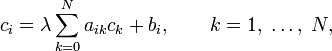

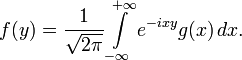

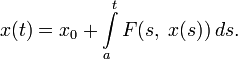

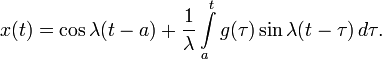
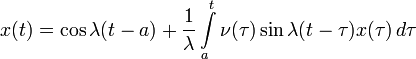
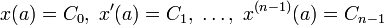

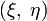 по некоторой кривой. Требуется определить эту кривую так, чтобы материальная точка, начав свое движение без начальной скорости в точке кривой с ординатой x , достигла оси Oξ за время t = f1(x) , где f1(x) — заданная функция.
по некоторой кривой. Требуется определить эту кривую так, чтобы материальная точка, начав свое движение без начальной скорости в точке кривой с ординатой x , достигла оси Oξ за время t = f1(x) , где f1(x) — заданная функция.