Интегральное уравнение фокса и ли

Дифракционная теория

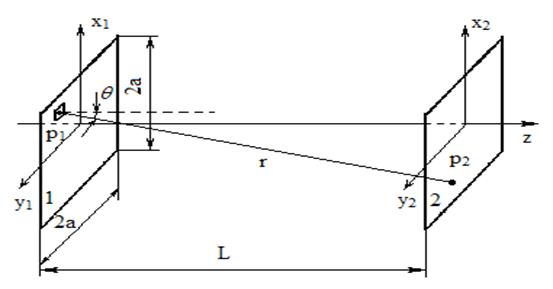
Строгое рассмотрение электромагнитного поля в открытом резонаторе основывается на системе уравнений Максвелла с заданными граничными условиями на зеркалах. Лазерные резонаторы имеют ту особенность, что их характерные размеры (длина резонатора, радиусы кривизны и апертуры зеркал) намного превышают длину волны излучения. Исходя из этого, можно считать, что электромагнитное поле в резонаторе является поперечным, однородно поляризованным. Для вычисления его стационарного распределения на поверхности одного из зеркал в виде интеграла от поля заданного на поверхности другого зеркала, можно воспользоваться скалярной формой принципа Гюйгенса-Френеля. Такие расчеты были впервые проведены Фоксом и Ли.

Рис. 1.23. К расчету плоскопараллельного резонатора с помощью дифракционного интеграла Кирхгофа.

Поле U_Р в любой р-ой зоне Френеля второго зеркала, обусловленное освещенным первым зеркалом, описывается поверхностным интегралом (дифракционный интеграл Кирхгофа):

(1.91)

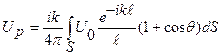
где 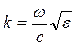— вектор распространения волны в среде; — расстояние от точки на первом зеркале до точки наблюдения: θ — угол между и перпендикуляром к поверхности первого зеркала; U₀-поле в плоскости первого зеркала. Моды резонатора соответствуют стационарным решениям интеграла (1.91).

Структуру поля для разных мод рассчитывают методом последовательных приближений с использованием ЭВМ. Следует отметить, что метод последовательных приближений здесь в некоторой степени адекватен самому физическому процессу в резонаторе при нарастании количества отражений. На рисунке 1.25 представлен результат расчета Фокса и Ли для амплитуды поля в точке x=a/2 на поверхности одного из зеркал в зависимости от числа отражений. Видно, что с увеличением количества отражений амплитуда поля принимает постоянное значение. 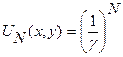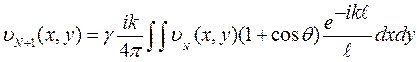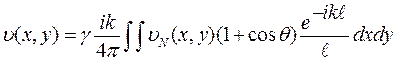После N прохождений, когда установился стационарный режим, можно написать соотношение: υ(x,y), где γ — комплексная постоянная, υ(x,y)-функция установившегося распределения. Подставляя ее в (1.91), получим: . Поскольку υ_N₊₁=υ_N, индексы в дальнейшем будем опускать и для нахождения структуры поля на поверхности зеркал, получаем интегральное уравнение: (1.92)

Собственные функции υ_mn(x,y), являющиеся решением интегрального уравнения (1.92) при соответствующих значениях γ_mn (собственные значения), характеризуют структуру поля на поверхности зеркал резонатора и обозначаются как колебания типа TEM_mn. (рис.1.25). Каждая поперечная мода включает в себя ряд продольных мод, которым соответствуют разные q.

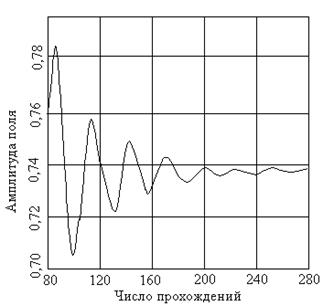Рис.1.24. Изменение амплитуды поля в зависимости от числа прохождений.

Для прямоугольных зеркал индекс m означает число изменений направления поля вдоль оси x, а индекс n – вдоль оси y. В случае круговых зеркал n означает число изменений направления поля по окружности (для фиксированного радиуса), а m— вдоль радиуса.

Логарифм собственных значений γ_mn является комплексной величиной

где β_mn определяет затухание за один проход, связанное с дифракционными потерями для каждой моды резонатора; α_mn определяет фазовый сдвиг за один проход, который прибавляется к геометрическому фазовому сдвигу.

Параметр β_mn характеризует добротность резонатора: 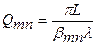. (1.94)

Из условия резонанса можно определить собственные частоты мод, которые выражаются через α_mn: 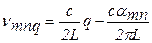. (1.95)

Таким образом, решение интегрального уравнения (1.92) для соответствующей конфигурации оптического резонатора дает информацию о структуре поля, резонансных частотах и дифракционных потерях резонатора. Заметим, что это уравнение имеет общий характер. Оно не связано с конкретной конфигурацией резонатора и формой зеркал и поэтому пригодно не только для плоских зеркал (резонатор Фабри-Перо), но и для зеркал иной формы (в частности, сферических).

На рис.1.26 показано распределение интенсивности для поперечных мод TEM_mn открытого резонатора.

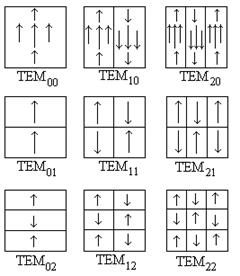Рис.1.25.Конфигурация электрического поля различных мод для квадратных зеркал.

Рис.1.26. Структуры электрических полей поперечных типов колебаний оптического резонатора.

Конспект лекций по дисциплине «Математический аппарат теории сигналов и систем» (стр. 5 )

Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4 5 6 7

15. Уравнение типа свертки

Это такие интегральные уравнения, ядро которых зависит от разности аргументов. Они имеют следующий вид:

Для решения уравнений типа свертки используется преобразование Фурье в следующей форме:

Введем понятие свертка функций. Она представляет из себя следующее:

Интегральный оператор Фурье будем обозначатьF(*).

Преобразование Фурье от свертки функций равно произведению отдельных преобразований Фурье от каждой функции:

Тогда после преобразования Фурье:

Отсюда можно найти :

Взяв обратное преобразование Фурье, мы получаем нашу функцию:

Пусть — это обратное преобразование Фурье от следующей функции:

Тогда решение можно найти по формуле:

16. Применение метода свертки для решения

интегральных уравнений 1-го рода

Бывают уравнения типа свертки и 1-го рода, то есть неизвестная функция есть только под знаком интеграла. Здесь также применим этот метод:

Преобразование Лапласа можно также применять как и Фурье, но нужно всегда при решении проверять область определения.

L — так будем обозначать преобразование Лапласа.

Взяв преобразование Лапласа от , получим:

Решение системы интегральных уравнений

Пусть имеем систему N интегральных уравнений следующего вида:

Применим ко всем уравнениям этой системы преобразование Лапласа:

Решив эту систему алгебраических уравнений в виде набора изображений и найдя от них оригиналы, мы найдем решение:

Это нелинейное уравнение типа свертки. Применим преобразование Лапласа к обеим частям этого уравнения:

Это квадратное уравнение, его решение:

17. Решение интегро-дифференциальных уравнений типа свертки

Пусть дано следующее интегро-дифференциальное уравнение:

Набор начальных условий:

Используется следующее свойство преобразования Лапласа:

Применим это к нашему уравнению:

Теперь общее уравнение превращается в следующий вид:

Отсюда изображение искомой функции:

Преобразование Меллина

Пусть есть некая функция и для нее справедливо следующее:

Для такой функции есть преобразование Меллина:

Преобразование Меллина устанавливает однозначную взаимосвязь между 2-мя функциями. Интеграл берется на комплексной плоскости вверх и вниз.

Гамма-функция. С помощью преобразования Меллина гамма-функция вводится следующим образом:

Преобразование Меллина во многом похоже на преобразование Лапласа:

Есть следующая взаимосвязь:

18. Применение преобразования Меллина для решения

;

Это свойство используется для решения интегрального уравнения вида:

. (*)

Преобразование Меллина используется для решения уравнений типа (*). Условие применимости этих функций состоит в том, чтобы они допускали от себя преобразование Меллина. Обозначим преобразование Меллина от через , а преобразование Меллина от — . Функции и должны иметь общую область аналитичности. Применим преобразование Меллина к обеим частям уравнения (*).

;

Пусть имеем интегральное уравнение вида:

;

19. Симметричные интегральные уравнения

Симметричными называются интегральные уравнения вида:

;

Если ядро комплексно — значное, то

;

— линейный оператор под функцией .

Если бы , то соответствующее интегральное уравнение стало бы однородным. При этом можно записать следующее: . Выяснили, что такое однородное уравнение имеет ограниченное число решений. Эти решения представляют собой набор некоторых функций . Они называются собственными функциями. Они однозначно соответствуют собственным числам.

Если мы рассматриваем симметричные ядра, то справедливы следующие свойства:

источники:

http://pandia.ru/text/80/170/54388-5.php