Интегралы уравнения эйлера бернулли лагранжа эйлера

Интегралы Лагранжа и Эйлера

Из дифференциальных уравнений движения невязкой жидкости [1]

(3.1)

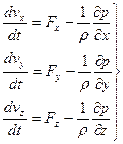
можно получить не только интеграл Бернулли. Для случая безвихревого движения невязкой жидкости возможно получить еще два интеграла – уравнения Эйлера и Лагранжа.

Для их вывода преобразуем выражение ускорения 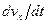. Произведем выкладки для плоского течения, а затем обобщим полученный результат на пространственный случай.

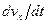
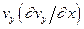
Запишем ускорение через местную и конвективную составляющую, добавив и вычтя в этом выражении член :

.

Перегруппировав члены в правой части этого выражения, получим

.

.

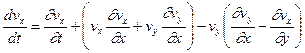
Используя выражение для проекции угловой скорости w_z, получим

.

С учетом сделанных преобразований, запишем проекции уравнения движения на ось x в виде

. (3.2 а)

Легко видеть, что для плоского течения . Обобщая этот вывод на пространственный случай течения, будем иметь

, (3.2 б)

. (3.2 с)

Уравнения (3.2 а-с), в которых в явной форме выделены кинематические особенности течения (угловые скорости) называются дифференциальными уравнениями в форме Громеко. В ряде случаев они более удобны для интегрирования, чем дифференциальные уравнения в форме Эйлера.

Для безвихревого течения жидкости справедливы следующие соотношения:

. (3.3)

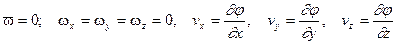
а также для массовых сил

, (3.4)

откуда потенциал массовых сил U получаем в виде .

Подставив равенства (3.3) и (3.4) в уравнения (3.2 а-с), учитывая, что

,

и перенося члены правой части в левую, будем иметь:

(3.5)

Из системы уравнений (3.5) следует, что сумма четырех слагаемых в квадратных скобках не зависит от координат, но является функцией времени. С учетом этого получим интеграл Лагранжа для неустановившегося потенциального течения

. (3.6)

Функция времени F(t), как правило, находится из граничных условий задачи.

Рассмотрим частный случай установившегося потенциального течения, в котором , а скорость и давление не зависят от времени

, (3.7)

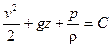
где постоянная 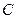одинакова для всех точек потока. Этот интеграл называется интегралом Эйлера. Его физический смысл тот же, что и для интеграла Бернулли: это выражение закона сохранения энергии.

Видно, что по форме интегралы Эйлера и Бернулли совпадают, но между ними, подчеркнем, имеется существенная разница: в интеграле Эйлера 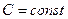для всего потока, а в интеграле Бернулли она постоянна лишь только вдоль линии тока.

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.043 сек.)

Интегралы уравнений Эйлера. уравнение Бернулли для идеальной жидкости.

Интегралы уравнений Эйлера. уравнение Бернулли для идеальной жидкости.

Интегралы уравнений Эйлера. уравнение Бернулли для идеальной жидкости. Для некоторых классов идеального потока жидкости можно получить общий Интеграл из уравнений Эйлера. Для этого мы используем векторный формат (5.43) dtai E = и X-й В связи со следующим течением. 1.Стабильный вихревой поток. Такой поток характеризуется достаточностью условия di1d (=0 и= = 0) на всем пространстве, которое является di 0d (=0 и 0).Из выражения (5.43), в данном случае айe = 0, т. е. sopz1 или * 9 * + = сопи! (5.51)） Сто один Важно подчеркнуть, что эта зависимость, называемая интегралом Бернулли, падает на все пространство, занимаемое жидкостью, которая, вероятно, будет двигаться. 2.Стабильный вихрь current. In в этом случае di / q1 = 0, но 0Φ0.И так оно и есть.、 bgayo5 = ih0. (5.52） Во-первых, предположим, что вектор и и о коллинеарны во всех точках определенной части движущейся жидкости. И| / a. In эта часть, E = 0 или e = = const.!Вы получите результат, соответствующий выражению (5.51).Это движение называется винтом.

Поскольку направление векторов поступательной и угловой скоростей совпадает в каждой точке, частицы движутся по нескольким линиям тока. Людмила Фирмаль

• Это одновременно и вихревая линия. То есть их основные сегменты действуют как мгновенные оси вращения отдельных частиц. Например, подобный ток может быть сформирован, когда он течет вокруг крыльев конечного span. In в случае такого течения условия не сохраняются! Живая секция не может быть нарисована, потому что она имеет значение= и = 0. Рассмотрим более общий случай вихревого течения, где векторы u и 0 не являются collinear. To получим Интеграл, выделим любой направленный отрезок yz (xx, yy, yy) и умножим его на обе стороны уравнения (5.52) скалярным образом. ^Гей-Э-йс =(э) s1z. Векторные произведения A =и X и являются векторами, нормально направленными к плоскости через векторы O и u(см. рис.5.2). так, если c1z совпадает с одним из них, то есть указывает направление линии потока или линии вихря, то векторы A и s3 ортогональны, а A x x s3 = 0.

• То есть вдоль линии потока и линии вихря, ss = sE = 0 или Е =Φ+& ^ = пост! (5.53)） Формула (5.53) аналогична формуле(5.51).Однако если в уравнении (5.51) величина E одинакова для всей движущейся жидкости, то в уравнении (5.53) она постоянна только вдоль постоянного потока или вихревой линии, причем от 1 из них к другому. Однако если провести вихревую линию через все точки линии потока и сформировать поверхность(рис.5.5), то, очевидно, функция E будет постоянной по всей поверхности. Аналогично, E = const! На поверхности образована система линий потока, проходящих через точки таких же вихревых линий. Если массовая сила является только гравитацией (Φ= qi), Интеграл Бернулли несжимаемой жидкости (p = coop!& = П / п)、 2 + ’m +’ ё ’= SOP81 ′ (5 * 54 102. Рисунок 5.5. E = построение поверхности, которая является SOP81 Это частный случай уравнения Бернулли (0) с вязким случаем (5.24). Для некоторых задач эффекты гравитации являются negligible. In кроме того, вместо r 0 p1 (pe) или r 0 IC (2c) и уравнения (5.54) уравнение Бернулли может быть использовано в следующем виде: П + Ж / Д * / 2 = Для идеального (невязкого) газа функция давления имеет разную форму для различных термодинамических условий. processes. In в случае баротропного процесса он выражается в основной функции.

Рассмотрим 2 особых случая. А. изотермического газового потока. Форма уравнения процесса имеет вид Не принимая во внимание неважную константу C, получим Интеграл Бернулли в виде: Φ+ ^ МНР + ^ = сопи! Ро * В случае газа этот Интеграл обычно используется в следующем виде, так как в большинстве технических задач сила массы не оказывает большого влияния на характер течения. Людмила Фирмаль

• −1П п + тр = сопи! Ро * Если точка, в которой давление равно p0, а величина скорости равна s0, то определим константу, принимая во внимание p01p0 = p1p, получим: ±1 ^ 1. + RMP_ ^ =0.(5.56） 2 1 Ro Ro B. подача газа изоляции. Форма уравнения процесса имеет вид Подставляя эту формулу (5.53) и учитывая незначительное влияние массовых сил, получаем уравнение Бернулли адиабатического движения идеального полного газа. (5.57)） _1_ для минусового «о, РО 2 ^ л-1 р»2-р-т = т ’^’ Уравнения(5.56) и(5.57)могут быть применены при тех же предельных условиях, что и интегралы Бернулли, которые они дают. С практической точки зрения имеет смысл использовать его только в том случае, если заметно проявляется сжимаемость газа, которая происходит со скоростью, сравнимой со скоростью звука. Уравнение Бернулли для несжимаемых жидкостей можно использовать для описания движения газа с низкой скоростью. 3.Нестационарный поток без vortices. In в этом случае di1d1Φ0 и 0 = 0.Последнее известное из кинематики условие соответствует наличию потенциала скорости 0p, который равен 0φφ = и. Поскольку речь идет о нестационарном движении, то Phi зависит не только от координат, но и от времени I. рассмотрим это как параметр. Вы можете написать уравнение.

Смотрите также:

Возможно эти страницы вам будут полезны:

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института