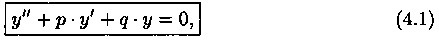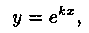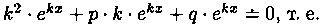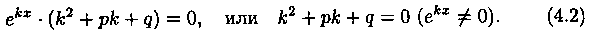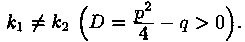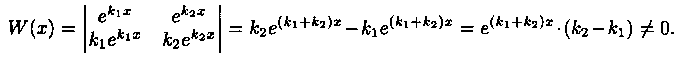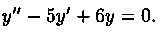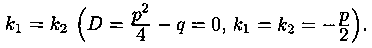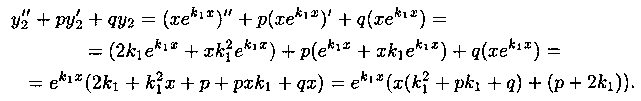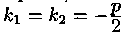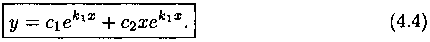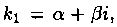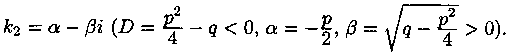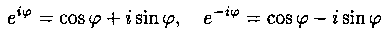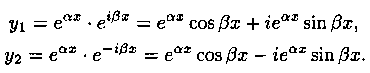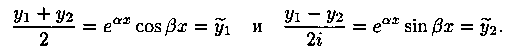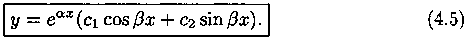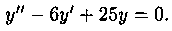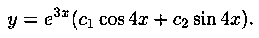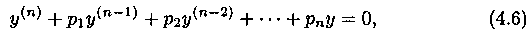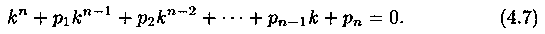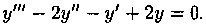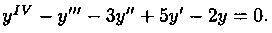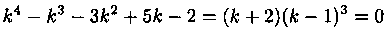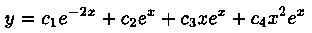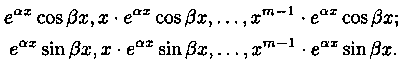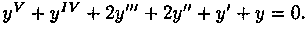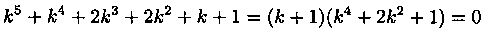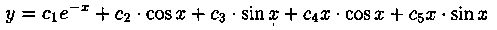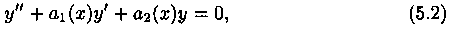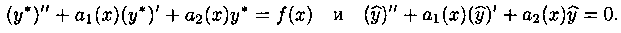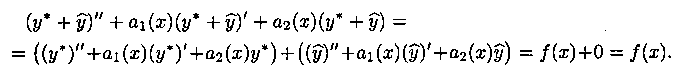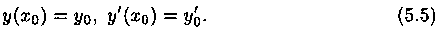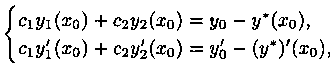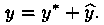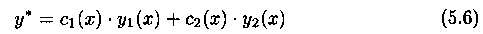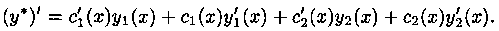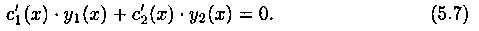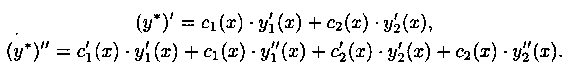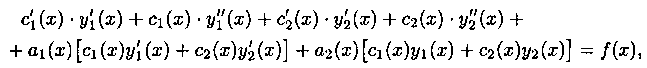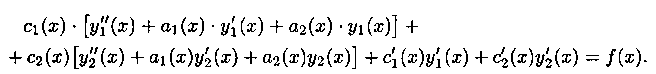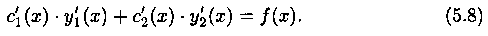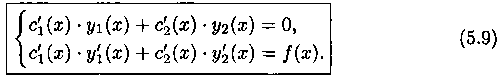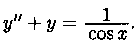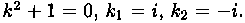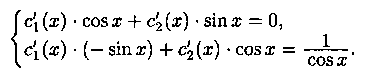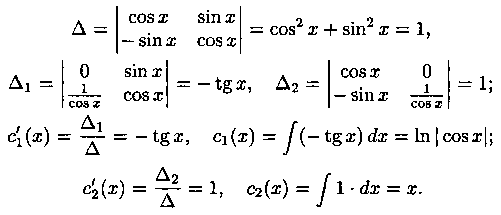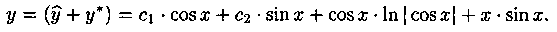Интегрирование линейных однородных уравнений порядка n

Лекция № 5

Ссылки

§4. ИНТЕГРИРОВАНИЕ ДУ ВТОРОГО ПОРЯДКА С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ

4.1. Интегрирование ЛОДУ второго порядка с постоянными коэффициентами

Частным случаем рассмотренных выше линейных однородных дифференциальных уравнений являются ЛОДУ с постоянными коэффициентами.

Пусть дано ЛОДУ второго порядка

где р и q постоянны.

Для нахождения общего решения уравнения (4.1) достаточно найти два его частных решения, образующих фундаментальную систему (см. теорему 3.5).

Будем искать частные решения уравнения (4.1) в виде

где k — некоторое число (предложено Л. Эйлером). Дифференцируя эту функцию два раза и подставляя выражения для у, у’ и у» в уравнение (4.1), получим:

Уравнение (4.2) называется характеристическим уравнением ДУ (4.1) (для его составления достаточно в уравнении (4.1) заменить у», у’ и у соответственно на k 2 , k и 1).

При решении характеристического уравнения (4.2) возможны следующие три случая.

Случай 1. Корни k₁ и k₂ уравнения (4.2) действительные и различные:

В этом случае частными решениями уравнения (4.1) являются функции y₁=e k1x и у₂=е _k2x. Они образуют фундаментальную систему решений (линейно независимы), т. к. их вронскиан

Следовательно, общее решение уравнения (4.1), согласно формуле (3.16), имеет вид

Пример 4.1. Решить уравнение

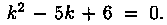
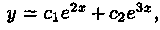
Решение: Составим характеристическое уравнение: Решаем его: k₁=2, k₂=3. Записываем общее решение данного уравнения: где c₁ и с₂ — произвольные постоянные (формула (4.3)).

Случай 2. Корни k₁ и k₂ характеристического уравнения (4.2) действительные и равные:

В этом случае имеем лишь одно частное решение y₁=e k1x. Покажем, что наряду с у₁ решением уравнения (4.1) будет и у ₂ =хе _k1x . Действительно, подставим функцию у₂ в уравнение (4.1). Имеем:

Но k₁ 2 +pk₁+q=0, т. к. k₁ есть корень уравнения (4.2); р+2k₁=0, т. к. по условию

Поэтому y»₂+Py’₂+qy₂=0, т. е. функция у₂=хе k1x является решением уравнения (4.1).

Частные решения 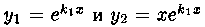образуют фундаментальную систему решений: W(x)=e 2k1x ≠0. Следовательно, в этом случае общее решение ЛОДУ (4.1) имеет вид

Случай3. Корни k₁ и k₂ уравнения (4.2) комплексные:

В этом случае частными решениями уравнения (4.1) являются функции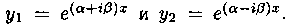По формулам Эйлера (см. Часть 1, п. 27.3)

Найдем два действительных частных решения уравнения (4.1). Для этого составим две линейные комбинации решений y₁ и у_2:

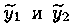
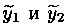
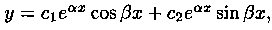
Функции являются решениями уравнения (4.1), что следует из свойств решений ЛОДУ второго порядка (см. теорему 3.2).Эти решения образуют фундаментальную систему решений, так как W(x) ≠ 0 (убедитесь самостоятельно!). Поэтому общее решение уравнения (4.1) запишется в виде или

Пример 4.2. Решить уравнение

Решение: Имеем: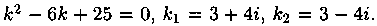По формуле (4.5) получаем общее решение уравнения:

Таким образом, нахождение общего решения ЛОДУ второго порядка с постоянными коэффициентами (4.1) сводится к нахождению корней характеристического уравнения (4.2) и использованию формул (4.3)-(4.5) общего решения уравнения (не прибегая к вычислению интегралов).

4.2. Интегрирование ЛОДУ n-го порядка с постоянными коэффициентами

Задача нахождения общего решения ЛОДУ n-го порядка (n > 2) с постоянными коэффициентами

где p_i, i= 1,n, — числа, решается аналогично случаю уравнения второго порядка с постоянными коэффициентами.

Сформулируем необходимые утверждения и рассмотрим примеры.

Частные решения уравнения (4.6) также ищем в виде у=е kх, где k — постоянное число.

Характеристическим для уравнения (4.6) является алгебраическое уравнение n-го порядка вида

Уравнение (4.7) имеет, как известно, n корней (в их числе могут быть и комплексные). Обозначим их через k₁, k₂, . k_n.

Замечание. Не все из корней уравнения (4.7) обязаны быть различными. Так, в частности, уравнение (k-3) 2 =0 имеет два равных корня: k1=k2=3. В этом случае говорят, что корень один (k=3) и имеет кратность mk=2. Если кратность корня равна единице: mk=1, его называют простым.

Случай 1. Все корни уравнения (4.7) действительны и просты (различны). Тогда функции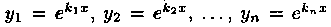являются частными решениями уравнения (4.6) и образуют фундаментальную систему решений (линейно независимы). Поэтому общее решение уравнения (4.6) записывается в виде

Пример 4.3. Найти общее решение уравнения

Решение: Характеристическое уравнение k 3 — 2k 2 — К+2=0 имеет корни k₁=-1, k₂=1, k₃=2. Следовательно, 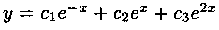общее решение данного уравнения.

Случай 2. Все корни характеристического уравнения действительные, но не все простые (есть корни, имеющие кратность м > 1). Тогда каждому простому корню К соответствует одно частное решение вида е кх, а каждому корню k кратности m>1 соответствует m частных решений: е kх, хе kх , х 2 е kx . х m-1 е kх.

Пример 4.4. Решить уравнение

Решение: Характеристическое уравнение

— общее решение уравнения.

Случай 3. Среди корней уравнения (4.7) есть комплексно-сопряженные корни. Тогда каждой паре a±β i простых комплексно-сопряженных корней соответствует два частных решения е ах cosβx и е ах sinβx, а каждой паре а ± β_i корней кратности m>1 соответствуют 2m частных решений вида

Эти решения, как можно доказать, образуют фундаментальную систему решений.

Пример 4.5. Решить уравнение

Решение: Характеристическое уравнение

имеет корни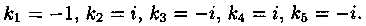Следовательно,

— общее решение уравнения.

§5. ЛИНЕЙНЫЕ НЕ ОДНОРОДНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ (ЛНДУ)

5.1. Структура общего решения ЛНДУ второго порядка

Рассмотрим ЛНДУ второго порядка

где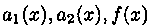— заданные, непрерывные на (а;b) функции. Уравнение

левая часть которого совпадает с левой частью ЛНДУ (5.1), называется соответствующим ему однородным уравнением.

Убедимся, что функция (5.3) — решение уравнения (5.1). Так как у* есть решение уравнения (5.1), а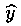— решение уравнения (5.2), то

В таком случае имеем:

Это означает, что функция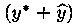является решением уравнения (5.1).

Покажем теперь, что функция

является общим решением уравнения (5.1). Для этого надо доказать, что из решения (5.4) можно выделить единственное частное решение, удовлетворяющее заданным начальным условиям

Продифференцировав функцию (5.4) и подставив начальные условия (5.5) в функцию (5.4) и ее производную, получим систему уравнений:

где у_о=у(х_о), у’₀=y'(x₀), с неизвестными c₁ и с₂. Определителем этой системы является определитель Вронского W(x₀) для функции y₁(x) и у₂(х) в точке х=х_о. Функции y₁(x) и у₂(х) линейно независимы (образуют фундаментальную систему решений), т. е.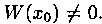Следовательно, система имеет единственное решение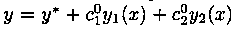: c₁=с 0 ₁ и с₂=с 0 ₂.

Решениеявляется частным решением уравнения (5.1), удовлетворяющим заданным начальным условиям (5.5). Теорема доказана.

5.2. Метод вариации произвольных постоянных

Рассмотрим ЛНДУ (5.1). Его общим решением является функция (5.3), т. е.

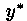
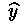
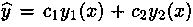
Частное решениеуравнения (5.1) можно найти, если известно общее решениесоответствующего однородного уравнения (5.2), методом вариации произвольных постоянных (метод Лагранжа), состоящим в следующем. Пусть— общее решение уравнения (5.2).Заменим в общем решении постоянные c₁ и с₂ неизвестными функциями c₁(x) и с₂(х) и подберем их так, чтобы функция

была решением уравнения (5.1). Найдем производную

Подберем функции c₁(x) и с₂(х) так, чтобы

Подставляя выражение для 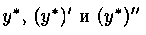в уравнение (5.1), получим:

Поскольку y₁(x) и у₂(х) — решения уравнения (5.2), то выражения в квадратных скобках равны нулю, а потому

Таким образом, функция (5.6) будет частным решением у* уравнения (5.1), если функции c₁(x) и с₂(х) удовлетворяют системе уравнений (5.7) и (5.8):

Определитель системытак как это определитель Вронского для фундаментальной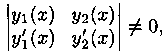системы частных решений у₁ (х) и у₂ (х) уравнения (5.2). Поэтому система (5.9) имеет единственное решение: с’₁(х)= j ₁(x) и с’₂(х)= j ₂(х), где j ₁(x) и j ₂(х) — некоторые функции от х. Интегрируя эти функции, находим c₁(x) и с₂(х), а затем по формуле (5.6) составляем частное решение уравнения (5.1).

Пример 5.1. Найти общее решение уравнения

Решение: Найдем общее решениесоответствующего однородного уравненияИмеем:Следовательно,

Найдем теперь частное решение у* исходногоуравнения. Оно ищется в виде (5.6):Для нахождения с₁(х) и с₂(х) составляем систему уравнений вида (5.9):

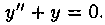
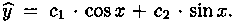
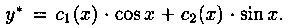
Запишем частное решение данного уравнения: 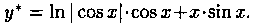Следовательно, общее решение данного уравнения имеет вид

При нахождении частных решений ЛНДУ может быть полезной следующая теорема.

Линейные однородные дифференциальные уравнения с постоянными коэффициентами

Содержание:

По этой ссылке вы найдёте полный курс лекций по математике:

Частный случай: уравнение второго порядка Пусть имеем линейное однородное дифференциальное уравнение второго порядка где р\, Р2 — действительные числа. Чтобы найти общее решение этого уравнения, надо найти два его линейно независимых частных решения. Следуя Эйлеру, будем искать их в виде где тогда Подставляя эти выражения для у и ее производных в уравнение (1), получаем .

Так как , то должно выполняться равенство Следовательно, функция у = eAz будет решением уравнения (1), т. е. будет обращать его в тождество по х, если А будет удовлетворять алгебраическому уравнению Уравнение (3) называется характеристическим уравнением по отношению к уравнению (1), а его левая часть называется характеристическим много-членом.

Уравнение (3) есть квадратное уравнение. Обозначим его корни через А] и 1 они могут быть 1) действительными и разными; 2) комплексными; 3) действительными и равными. Рассмотрим каждый случай в отдельности. 1. Если корни Л|, Аг характеристического уравнения действительные и разные, то частными решениями уравнения (1) будут функции Эти решения линейно независимы (Aj Ф А2) и, следовательно, образуют фундаментальную систему решений уравнения.

Общее решение уравнения

Общее решение уравнения имеет вид — произвольные постоянные). Пример 1. Найти общее решение уравнения М Составляем характеристическое уравнение: Оно имеет корни Линейные однородные дифференциальные уравнения с постоянными коэффициентами Общий случай: уравнение произвольного порядка Физические приложения: уравнение колебаний Уравнения, приводящие к уравнениям с постоянными коэффициентами Линейные неоднородные дифференциальные уравнения Отсюда получаем искомое общее решение 2.

Пусть корни характеристического уравнения комплексные. Так как коэффициенты р], р2 характеристического уравнения действительные, комплексные корни входят попарно сопряженными. Положим, что Частные решения дифференциального уравнения (1) можно записать в виде Это комплекснозначные функции действительного аргумента х, а мы будем заниматься лишь действительными решениями.

С помощью формул Эйлера частные решения ij\ и у2 уравнения (1) можно представить в виде Воспользовавшисьтеоремой 4, получим, что частными решениями уравнения (1) будут также функции _ Эти решения линейно независимы, так как Решения образуют фундаментальную систему решений уравне-ния (1), общее решение которого в этом случае имеет вид или Пример 3.

Найти общее решение уравнения 4 Характеристическое уравнение имеет кратные корни Поэтому общее решение исходного дифференциального уравнения: Замечание. Пусть имеем линейное однородное дифференциальное уравнение (вообще, с переменными коэффициентами) Пусть — частное решение уравнения. Введем новую искомую функцию ti(x) соотношением (разрешимым относительно н(х) в тех интервалах, где yi(x) не обращается в нуль).

Из этого соотношения найдем производные от у : и подставим их в уравнение (5): Для функции и(х) получаем опять уравнение порядка п, но коэффициент при м(х) есть £(yil-Он тождественно равен нулю, так как yi (х) есть решение уравнения (5). Следовательно, в полученном уравнении порядок понизится, если ввести новую искомую функцию z(x) = и'(х).

Разделив, кроме того, все члены последнего уравнения на yi(x) Ф 0, приведем его к виду Итак, если известно частное решение уравнения (5), то задача интегрирования этого уравнения приводится к интегрированию линейного однородного уравнения порядка п — \. Можно показать, что если известны два частных линейно независимых решения, то порядок уравнения может быть понижен на две единицы. Вообше, если известно г частных линейно независимых решений линейного однородного дифференциального уравнения, то порядок этого уравнения может быть понижен на г единиц. 6.2.

Физические приложения: уравнение колебаний Линейные дифференциальные уравнения с постоянными коэффициентами возникают в задачах о механических и электрических колебаниях. Рассмотрим уравнение свободных механических колебаний, причем независимой переменной будем считать время t: где у — отклонение колеблющейся точки от положения равновесия, rh — масса точки, h — коэффициент трения (считаем, что сила трения пропорциональна скорости), к > 0 — коэффициент упругости восстанавливающей силы (считаем, что эта сила пропорциональна отклонению).

Характеристическое уравнение

Характеристическое уравнение для (6) имеет корни Если трение достаточно велико, h2 > Атк, то эти корни действительные и отрицательные. Общее решение уравнения (6) в этом случае имеет вид Так как то из (7) заключаем, что при большом трен и и отклонение точки от положения равновесия с возрастанием t стремится к нулю, не совершая колебаний. Если трение мало, Атк, то характеристическое уравнение имеет комплексно сопряженные корни Общее решение уравнения (6) в этом случае определяется формулой или Отсюда видно, что в случае малого трения происходят затухающие колебания. Пусть теперь трение отсутствует, .

В этом случае характеристическое уравнение имеет чисто мнимые корни Решение уравне- ния (6) имеет вид . в этом случае происходят незатухающие гармонические колебания с частотой ш = и произвольными амплитудой А и начальной фазой 6. Задача. При каких 1) все решения уравнения стремятся к нулю при 2) каждое решение уравнения обращается в нуль на бесконечном множестве точек х? 6.3. Общий случай: уравнение произвольного порядка Рассмотрим теперь линейное однородное дифференциальное уравнение произвольного порядка п (п ^ 1) с постоянными коэффициентами ) гдерьрг,,Рп — действительные числа.

Общее решение дифференциального уравнения (8) находим так же, как и в случае уравнения второго порядка. Ищем решение в виде Подставляя вместо у величину еХх в уравнение (8), получаем , что приводит к характеристическому уравнению 2. Находим корни характеристического уравнения. 3. По характеру корней выписываем частные линейно независимые решения уравнения (8), руководствуясь тем, что: а) Каждому действительному однократному корню А характеристическою уравнения соответствует частное решение уравнения (8).

б) Каждой паре однократных комплексно сопряженных корней соответствуют два линейно независимых частных решения уравнения (8). в) Каждому действительному корню А кратности г соответствует г линейно независимых частных решений уравнения (8). Рассмотрим случай в) подробнее. Пусть число А есть корень кратности г характеристического уравнения . Функцию будем рассматривать как функцию двух аргументов: ж и А.

Возможно вам будут полезны данные страницы:

Она имеет непрерывные производные по а: и по А всех порядков, причем Поэтому частные производные функции по х и по А не зависят от порядка дифференцирования (операции дифференцирования функции у по х и по А перестановочны), так что Воспользовавшись этой перестановочностью, а также тем, что Если А есть г-кратный корень характеристического уравнения то стало быть, правые части (10) и (11) тождественно по х равны нулю: Это означает, что функции являются в этом случае решениями уравнения (8).

Легко проверить, что функции линейно независимы на любом интервале (a, b) изменения х. г) Приведенные в пункте в) рассуждения сохраняют силу и для комплексных корней.

Поэтому каждой паре комплексно сопряженных корней p кратности \l отвечает 2/х частных решений уравнения 4. Число построенных таким образом частных решений уравнения (8) равно порядку п этого уравнения. Можно показать, что все эти решения линейно независимы в совокупности. Имея п линейно независимых частных решений 3/i(x), skfc). уп(я) уравнения (8), получаем общее решение этого уравнения, где произвольные постоянные. Прммер 4. Найти общее решение уравнения Составляем характеристическое уравнение: 2. Находим корни характеристического уравнения: 3.

По характеру корней выписываем частные линейно независимые решения дифференциального уравнения: 4. Общее решение дифференциального уравнения имеет вид Схема решения линейного дифференциального уравнения с постоянными коэффициентами Дифференциальное уравнение действительные числа). Характеристическое уравнение Корни характеристического уравнения Частные линейно независимые решения дифференциального уравнения Общее решение уравнения — произвольные постоянные). §7.

Уравнения, приводящие к уравнениям с постоянными коэффициентами Существуют линейные дифференциальные уравнения с переменными коэффициентами, которые с помощью замены переменных преобразуются в уравнения с постоянными коэффициентами. К их числу принадлежит уравнение Эйлера где pi.tp2, —tPn — постоянные числа.

Ограничимся рассмотрением уравнения Эйлера 2-го порядка (оно встречается в задачах математической физики): Линейные однородные дифференциальные уравнения с постоянными коэффициентами Общий случай: уравнение произвольного порядка Физические приложения: уравнение колебаний Уравнения, приводящие к уравнениям с постоянными коэффициентами Линейные неоднородные дифференциальные уравнения Положим Подставляя выражения для , получим дифференциальное уравнение с постоянными коэффициентами.

Последнее интегрируется обычным приемом: составляем характеристическое уравнение находим его корни и по характеру корней выписываем общее решение уравнения (2), после чего возвращаемся к старой переменной х. Пример. Найти общее решение уравнения Замена переменной х = приводит к уравнению характеристическое уравнение которого имеет корни Общее решение преобразованного уравнения равно Учитывая, что , для общего решения исходного уравнения получаем выражение Замечание 1.

Для преобразованного уравнения (2) в случае действительных и различных корней характеристического уравнения (3) частные решения имеют вид Поэтому можно сразу задаться этим видом частного решения. Подставляя в уравнение (1), получим для к уравнение ) совпадающее с (3). Каждому простому действительному корню уравнения (4) отвечает частное решение уравнения (1); двукратному корню отвечают два решения уравнения (1).

Паре комплексных сопряженных корней уравнения (4) будут соответствовать два решения уравнения (I). Замечание 2. Уравнение постоянные числа) подстановкой также приводится к уравнению с постоянными коэффициентами. §8. Линейные неоднородные дифференциальные уравнения Линейное неоднородное дифференциальное уравнение п-го порядка имеет вид Здесь заданные на некотором интервале (а, р) функции. Если ао(ж) Ф 0 на (а, то после деления на ац(х) получим уравнение.

Из теоремы 1 существования и единственности решения задачи Коши получаем: если на отрезке [а, 6] коэффициенты Рк(х) и правая часть /(х) уравнения (2) непрерывны, то это уравнение имеет единственное решение, удовлетворяющее условиям Уравнение (2) можно записать в виде где, как и выше, Теорема 12. Если у(х) есть решение неоднородного уравнения есть решение соответствующего однородного уравнения мПо условию, В силу линейности оператора £ имеем Это означает, что функция есть решение уравнения Теорема 13.

Если у\(х) есть решение уравнения есть решение уравнения та функция есть решение уравнения По условию, используя линейность оператора £, получаем Последнее означает, что функция есть решение уравнения Теорема выражает так называемый принцип суперпозиции (наложения). Теорема 14. Если уравнение где все коэффициенты и функции действительные, имеет решение то действительная часть решения и(х) и его мнимая часть v(x) являются соответственно решениями уравнений.

По условию имеем Отсюда получаем: Теорема 15 (о структуре общего решения линейного неоднородного дифференциального уравнения). Общее решение в области — уравнения с непрерывными на отрезке коэффициентами , и правой частью f(x) равно сумме общего решения соответствующего однородного уравнения и какого-нибудь частного решения у(х) неоднородного уравнения, т. е. Надо доказать, что где произвольные постоянные, линейно независимые решения соответствующего однородного уравнения £[у] = 0, является общим решением неоднородного уравнения.

Будем исходить из определения общего решения и просто проверим, что семейство функций у(ж), определяемое формулой (4), удовлетворяет условиям 1) и 2), содержащимся в этом определении. В самом деле, функция у(х), определяемая формулой (4), является решением уравнения (2) при любых значениях постоянных, поскольку сумма какого-либо решения неоднородного уравнения и любого решения соответствующего однородного уравнения есть решение неоднородного уравнения.

Так как для уравнения (2) при х 6 [а, Ь] выполнены условия теоремы 1 существования и единственности решения задачи Коши, то остается показать, что подбором постоянных С\, в (4) можно удовлетворить произвольно заданным начальным условиям где хо € (а,6), т.е. можно решить любую задачу Коши. Ограничимся случаем, когда п = 3.

Потребовав, чтобы решение (4) удовлетворяло начальным условиям (5), приходим к системе уравнений для отыскания Эта линейная по отношению к система трех уравнений с тремя неизвестными допускает единственное решение относительно з при произвольных правых частях, так как определитель этой системы есть определитель Вронского W(x$) для линейно независимой системы решений соответствующего однородного уравнения и, следовательно, отличен от нуля в любой точке ж € (а, Ь), в частности в точке ж = жо.

уо, Уо> Уо» найдется решение С?, С?, Cj системы (6) такое, что функция будет решением дифференциального уравнения (2), удовлетворяющим начальным условиям Линейные однородные дифференциальные уравнения с постоянными коэффициентами Общий случай: уравнение произвольного порядка Физические приложения: уравнение колебаний.

Уравнения, приводящие к уравнениям с постоянными коэффициентами Линейные неоднородные дифференциальные уравнения Из этой теоремы следует, что задача нахождения общего решения линейного неоднородного уравнения сводится к отысканию какого-либо частного решения этого неоднородного уравнения и общего решения соответствующего однородного уравнения. Интегрирование линейного неоднородного дифференциального уравнения методом вариации постоянных 155 Пример 1.

Найти общее решение уравнения М Нетрудно заметить, что функция является частным решением данного неоднородного уравнения. Чтобы найти общее решение этого уравнения, остается отыскать общее решение соответствующего однородного уравнения Это уравнение есть линейное однородное уравнение с постоянными коэффициентами. Характеристическое уравнение, соответствующее уравнению , есть корни его Поэтому общее решение уравнения (*) имеет вид . Общее решение исходного неоднородного уравнения:

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.

Интегрирование однородных линейных систем ДУ
с постоянными коэффициентами. Метод Эйлера

Линейной однородной системой с постоянными коэффициентами называется система дифференциальных уравнений вида

где коэффициенты — постоянные, а — искомые функции от .

Систему (1) можно коротко записать в виде одного матричного уравнения

называется частным решением уравнения (2) в интервале , если выполняется тождество

Система частных решений

(здесь в записи нижний индекс указывает номер решения, а верхний — номер функции в решении) называется фундаментальной на интервале , если ее определитель Вронского

Теорема. Если система частных решений однородного уравнения (2) является фундаментальной, то общее решение этого уравнения имеет вид

где — произвольные постоянные.

Линейные системы можно интегрировать различными способами, рассмотренными ранее, например методом исключения, путем нахождения интегрируемых комбинаций и т.д.

Для интегрирования однородных линейных систем с постоянными коэффициентами применяется также метод Эйлера .

Рассмотрим этот метод в применении к системе трех линейных дифференциальных уравнений:

Решение системы (3) ищем в виде

Подставляя (4) в (3) и сокращая на , получаем систему уравнений для определения и

Система (5) имеет ненулевое решение, когда ее определитель равен нулю,

Уравнение (6) называется характеристическим .

А. Пусть корни и характеристического уравнения — вещественные и различные . Подставив в (5) вместо число и решив систему (5), получим числа и . Затем положим в (5) и получим числа и, наконец, при получим и . Соответственно трем наборам чисел и получим три частных решения

Общее решение системы (3) имеет вид

Пример 1. Решить систему дифференциальных уравнений

Решение. Составляем характеристическое уравнение

Корням соответствуют числа

Выписываем частные решения

Общее решение системы:

Б. Рассмотрим теперь случай, когда корни характеристического уравнения комплексные .

Пример 2. Решить систему линейных однородных дифференциальных уравнений

Решение. Выпишем систему для определения и

имеет корни . Подставляя в (8), получаем два уравнения для определения и

из которых одно является следствием другого (в силу того, что определитель системы (8) равен нулю).

Возьмем , тогда первое частное решение запишется так:

Аналогично, подставляя в (8) корень , найдем второе частное решение:

Перейдем к новой фундаментальной системе решений:

Пользуясь известной формулой Эйлера , из (9), (10) и (11) получаем

Общим решением системы (7) будет

Замечание. Найдя первое частное решение (9), можно было бы сразу написать общее решение системы (7), пользуясь формулами

где и обозначают соответственно действительную и мнимую части комплексного числа , т. е. если , то , .

В. Случай кратных корней.

Пример 3. Решить систему

Решение. Характеристическое уравнение

Решение следует искать в виде

Подставляя (13) в первое уравнение системы (12), получаем

Приравнивая коэффициенты при одинаковых степенях в левой и правой части (14), получаем:

Величины и остаются произвольными. Обозначая их соответственно через и , получаем общее решение системы (12):

Замечание. Легко проверить, что если (13) подставить во второе уравнение системы (12), то получим тот же результат (15). В самом деле, из равенства

получаем два соотношения для определения и через и

Пример 4. Решить задачу Коши для системы линейных дифференциальных уравнений

с начальными условиями .

Решение. Характеристическое уравнение

Корни уравнения (17): . Действительному корню отвечает решение

Подставляя (18) в систему (16) и сокращая на , получаем

откуда . Полагаем, например, , тогда и частное решение (18):

Комплексному корню отвечает решение

подставив которое в (16) и сокращая на , получим

откуда , так что, например, при имеем и частное решение

Корню соответствует решение, комплексно сопряженное решению (20), т.е.

Учитывая (19), (20), (21), получаем общее решение

Выделим, наконец, решение с начальными условиями . Из (22) при имеем

Воспользовавшись формулами Эйлера , окончательно получим