Дифференциальное уравнение упругой линии балки и его интегрирование

При изгибе ось балки искривляется, а поперечные сечения перемещаются поступательно и поворачиваются вокруг нейтральных осей, оставаясь при этом нормальными к изогнутой продольной оси (рис. 8.22). Деформированная (изогнутая) продольная ось балки называется упругой линией , а поступательные перемещения сечений, равные перемещениям y = y ( x ) их центров тяжести сечений – прогибами балки .

Между прогибами y ( x ) и углами поворота сечений θ ( x ) существует определенная зависимость. Из рис. 8.22 видно, что угол поворота сечения θ равен углу φ наклона касательной к упругой линии ( θ и φ — углы с взаимноперпендикулярными сторонами). Но согласно геометрическому смыслу первой производной y / = tg θ . Следовательно, tg θ = tg φ = y / .

В пределах упругих деформаций прогибы балок обычно значительно меньше высоты сечения h , а углы поворота θ не превышают 0.1 – 0.15 рад. В этом случае связь между прогибами и углами поворота упрощается и принимает вид θ = y / .

Определим теперь форму упругой линии. Влияние перерезывающих сил Q на прогибы балок, как правило, незначительно. Поэтому с достаточной точностью можно принять, что при поперечном изгибе кривизна упругой линии зависит только от величины изгибающего момента M z и жесткости EI z (см. уравнение (8.8)):

.

В то же время в неподвижной системе координат кривизна упругой линии, как и всякой плоской кривой,

.

Приравнивая правые части (8.26) и (8.27) и учитывая, что правила знаков для M z и y // были приняты независимо друг от друга, получаем

.

Это равенство называется дифференциальным уравнением упругой линии . При малых деформациях второе слагаемое в знаменателе мало по сравнению с единицей (при θ = 0.1 рад ( y / ) 2 =0.01 ) и им можно пренебречь. В результате получим приближенное дифференциальное уравнение упругой линии балки

.

Выбор знака в правой части (8.29) определяется направлением координатной оси y , так как от этого направления зависит знак второй производной y // . Если ось направлена вверх, то, как видно из рис. 8.23, знаки y // и M z совпадают, и в правой части надо оставить знак плюс. Если же ось направлена вниз, то знаки y // и M z противоположны, и это заставляет выбрать в правой части знак минус.

Заметим, что уравнение (8.29) справедливо только в пределах применимости закона Гука и лишь в тех случаях, когда плоскость действия изгибающего момента M z содержит одну из главных осей инерции сечения.

Интегрируя (8.29), находим сначала углы поворота сечений

,

а после второго интегрирования – прогибы балки

.

Постоянные интегрирования определяются из граничных условий. На участках с различными аналитическими выражениями для изгибающих моментов дифференциальные уравнения упругой линии также различны. Интегрирование этих уравнений при n участках дает 2 n произвольных постоянных. Для их определения к граничным условиям на опорах добавляются условия равенства прогибов и углов поворота на стыке двух смежных участков балки.

Интегрирование дифференциального уравнения изогнутой оси балки при двух участках.

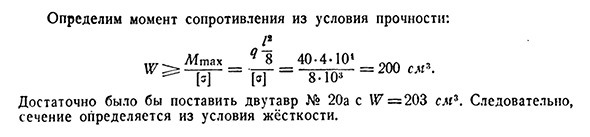
Интегрирование дифференциального уравнения изогнутой оси балки при двух участках.

• Интеграл дифференциальных уравнений криволинейной оси балки на двух участках. Если изгибающий момент в разных частях балки представлен разными формулами, то необходимо составить такое же количество дифференциальных уравнений, как и площадь на балке. Нагружают силой р на расстоянии от левой балки на двух опорах

в пролете Z, b от правой кромки b; пусть a » >B(рис. 287). Поддерживающий отклик луча равен H A=0, B=^ -. Возьмите начало координат левой опоры и правую ось X. Изгибающий момент в первом и втором сечениях выражается различными уравнениями^поэтому мы можем найти два произвольных сечения в абсциссах x^и x%. Значения y, M, C, D и абсциссы раздела

уравнения отмечены в индексе 1 первого раздела и индексе 2 второго. При Людмила Фирмаль

составлении моментального представления обеих секций рассмотрим левую часть балки, а затем первую секцию: l R Ml=LX1=Y Xi, для второй секции (секция O2): R М=А% — Р(х2-а)= — х — р(х2-а). Интегрирование термов вида P (x2-a) осуществляется без скобок, как это сделано в Примере 74. При этих условиях вычисление выглядит следующим образом: П Е Р В ы й Г А С Т О К Т О Р У ч а с Т О К А Д=M1=Dx1; EJy= — (18.31) Ежи’и=L42=DH2-Р(х2-а); ежи и=-Р(х2-а); с т Pbxl +(18.33) 4-C2×2 4-D2. (18.34) выражение для отклонения и вращения включает Интеграл четырех констант. Чтобы определить эти константы, нужно

написать четыре уравнения. Эти уравнения, как и в предыдущем случае, что-то знают о прогибе и угле поворота, всегда можно сделать, рассматривая сечение пучка таким сечением вещества является: Участок с, расположенный на границе двух участков, можно отнести как к первому, так и ко второму из них. Итак, величину прогиба и угла поворота сечения С можно вычислить как по формуле первого сечения, так и по формуле второго: то есть x1=x2=a; Если значение получено и B1=9a или y и 0, то оно должно быть одинаковым. Ежи=Ежи Альф () е дя^^е дя^. (b)§ 112]уравнение

криволинейной оси балки в двух сечениях 363 Таким образом, точки деления графика всегда дают два уравнения. Сечение A при x t=0 отклонение YG=O, ©> «B«x=I>y2=0. Подставляя выражения (18.31) и (18.33) вместо X>и уравнивая значение и правильную часть X% a, получаем условие (a): P A2|p_ _ R a * g>(A

°) 8 I2-I2P2 Откуда (18.35)) Аналогично она получается по условиям из формул (18.32) и (18.34 (&): 7• + ЦРУ+°я=7^ — П(°Б-«Б» Б Д Откуда Di=D(18.36) следовательно, константы интегрирования для обоих участков были одинаковыми. Это связано с принятием метода композиции и интегрирования

дифференциальных уравнений. Когда Формула (18.32) применяется к эталонному участку D, она получается на основе © Oh=09, следовательно, O9=0. Применение той же формулы (18.34) к ссылочному разделу B дает результаты, основанные на (d Здесь уравнения для y и 6 принимают следующий вид: 364 аналитические методы определения деформации[глава XV. Рассмотрим значение максимального прогиба f. это будет сечение с 0=0. Из формулы для 0! Мы видим это для X1=0., РА’ЗЕЛ площадь поперечного сечения В=а (И — #); Так как B O. Таким образом, 0t

между точкой А и точкой с меняет знак, то есть проходит через ноль. Людмила Фирмаль

Значит, наибольший прогиб будет у первого участка. Чтобы найти абсциссу xj соответствующего сечения, подставим это значение xj в выражение 0A и сделаем его равным нулю: — -^ -(/2 — £2) | = 0; таким образом, xj=1 — • Поэтому при перемещении от середины пролета к опоре Фигура. Центральный прогиб пролета 287 Два. В этом легко убедиться, подсчитав небольшую разницу между Если вы присваиваете выражению Y lf, RZ (R-B) / z (R-B*)RRU’Z l /

((18 37) 27EJZ-21EJ V\Z2/’ Расстояние участка с наибольшим отклонением

от левой опоры изменяется с изменением положения груза. Если сила P находится в середине пролета、 /. £Р/5 −2’Max-4 8£/, (18.38) Если переместить силу P на правую опору и установить предельное расстояние b равным нулю, то#->0; x0=—=x= = 0,577/. Tplt/ Из точек D и B (рис. 288) абсцисса точки с наибольшим отклонением изменяется только между 0,5/и 0,577 / между точками D и R. особенно при размещении Фигура. 288. (18.39) Число /Ш В Я/^.§ 1 1 2] формула для криволинейной оси балки на двух участках 3 6 5 П р и М Е Р 77.

Подобрать сечение стальной двутавровой балки с непрерывной нагрузкой q=4 т/м на полпролета(рис. 289), если пусковое напряжение[а]=1000кг/см2, а допустимое отклонение не должно превышать-jOOQ-пролет равен/=2,0 м. Давайте положим начало координат в точке I, ось x находится справа, а ось y-вверху. Нумерация участков показана на рисунке. Мы составляем и интегрируем дифференциальные уравнения криволинейных осей, считая

x на обоих участках от точки A. fl- Два. Фигура. Двести восемьдесят девять ЭДЖ ЭДЖ d2y * ДХ% Т О Р О й=м2, у ч а с т о с д Х2″2\2 2)’ EJys— — ^4″ —— 2^> ^2* Один. Два. Интегральная константа определяется из условия: x3= / » x » должно быть 2 = / >» ^8 = 0. х t=хз я Два» >> акстись Д х s’ >X i=X s I −2 >Эжит=Эжит. Дайте первые два условия: с 2_|?/ 8р-7?/ 4-7?/ 4 * ■48 ′ 16-24-384 * Из третьего и четвертого условий: Ди = ДС = 7?/ 4 Триста восемьдесят четыре Запишите уравнение прогиба первой секции в последней форме, так как максимальное прогибание будет иметь конец балки. Y ’

[+48 ′ 384J-384EJ L8I+G Максимальное отклонение (x=0)/= — Iql * WAEJ * Теперь мы можем

определить J: / _ из жестких условий. 7^ — 3 8 4£7′ Iql 7.40-8- 10E-103 384.2-10° 7= = 2910см. I балка № 24 момент инерции 7=3460см\366 метод анализа для определения деформации[гл. XVIII Определите момент сопротивления из условий интенсивности: Afmax8″ — — — Т Т-8-10″ — * * * см>’ I луч No. It достаточно разместить 20A С W=203cm*. Таким образом, поперечное сечение определяется из условий жесткости.

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Метод интегрирования дифференциального уравнения изгиба балки

Наиболее естественным методом определения функции прогибов является метод непосредственного интегрирования уравнения изгибающих моментов.

$EI\,y»(x) = M(x)$ – полученное дифференциальное уравнение;

$EI\,y'(x) = EI\,\varphi (x) = \int dx + C$ – первый интеграл (уравнение углов поворота);

$EI\,y(x) = \int dx = \iint dxdx + C\,x + D$ – второй интеграл (уравнение прогибов).

Кроме интегрирования уравнения изгибающих моментов $M(x)$, для получения уравнения прогибов необходимо определить две постоянных интегрирования $C$ и $D$ из условий закрепления балки. При этом надо учесть, что шарнирная опора исключает прогибы балки, а жесткое зажатие – прогибы и углы поворота (то есть они равны нулю).

Физический смысл постоянных интегрирования такой: при $x = 0$ угол поворота $EI\,\varphi (0) = C$, а прогиб $EI\,y(0) = D$, то есть константа $C$ равна углу поворота в начале координат, константа $D$ равна прогибу балки при x=0.

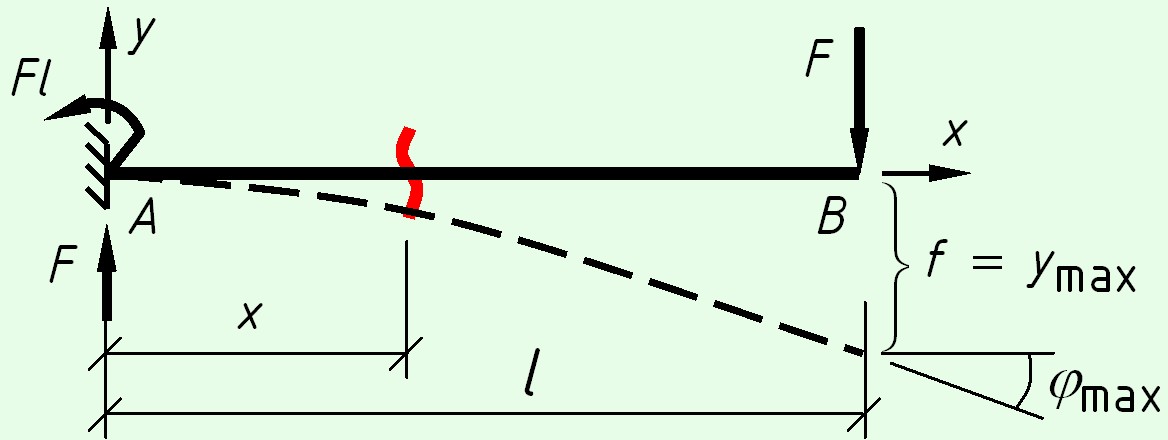
Консольная балка с силой на конце

На левой опоре возникают реакции – вертикальная сила $F$ и момент $M = F \cdot l$.

Уравнения изгибающих моментов

$M(x) = — Fl + Fx = F(x — l)$

Уравнение углов поворота

$EI\,y'(x) = EI\,\varphi (x) = \int dx + C = F(\frac<<>> <2>— lx) + C$

Так как в сечении $A$ (в защемлении) отсутствует прогиб и угол поворота, получим следующую систему уравнений

$\left\ < \beginEI\,\varphi (0) = F(\frac<<<0^2>>> <2>— l \cdot 0) + C = 0 \hfill \\ EI\,y(0) = F(\frac<<<0^3>>> <6>— l\frac<<<0^2>>><2>) + C \cdot 0 + D = 0. \hfill \\ \end \right.$

Решение этой системы уравнений приводит к результату $C = 0$, $D = 0$.

Окончательно функция прогибов для рассматриваемой балки имеет вид

Максимальный прогиб будет иметь место при $x = l$

где знак « – » указывает направление перемещений – в сторону, противоположную положительному направлению оси $y$. Стрела прогиба $f = \frac<>><<3\,EI>>$.

Максимальный угол поворота сечения также будет иметь место при $x = l$

знак « – » указывает направление угла поворота – сечение поворачивается по часовой стрелке.

Шарнирно закрепленная балка с силой посередине

На опорах возникают вертикальные реакции $ = = F/2$.

Поскольку уравнение изгибающих моментов разное на двух разных участках, функция прогибов также будет разная. Используя полную симметрию расчетной схемы, далее будем рассматривать только левый участок, для которого уравнение изгибающих моментов имеет вид

$M(x) = \frac<2>x$, то есть $EI\,y»(x) = \frac<2>x$, интегрируем дважды

Константы интегрирования $C$ и $D$ полученного уравнения справедливы только для первого участка, поэтому их необходимо определять из условий, связанных с перемещениями на первом участке. Такими условиями является равенство нулю прогибов на опоре $A$ ($x = 0$) и, исходя из симметрии, равенство нулю угла поворота под силой $F$ ($x = l/2$). Имеем систему уравнений

Окончательно функция прогибов для рассматриваемой балки имеет вид

Максимальный прогиб будет иметь место при $x = l/2$

Максимальные углы поворота сечений будут на опорах ($x = 0$ и $x = l$).

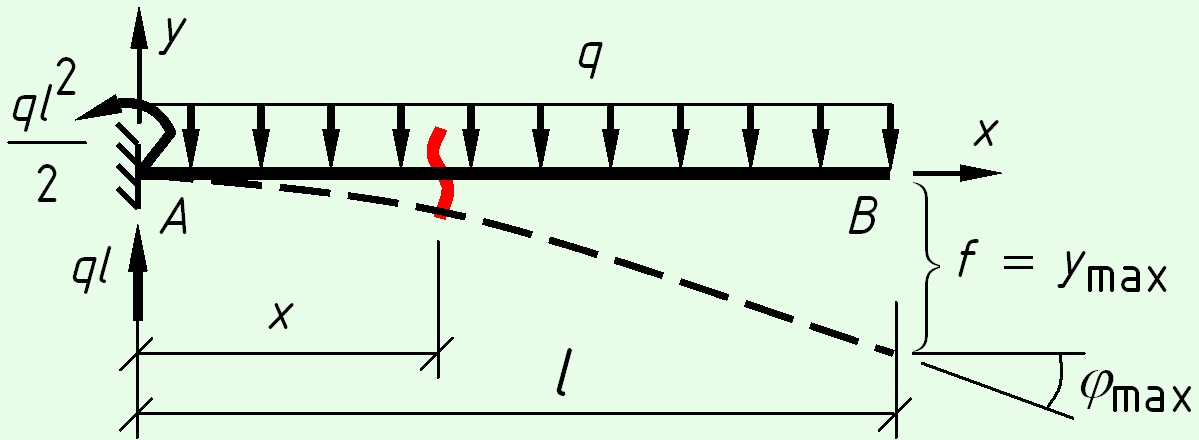
Консольная балка с равномерно распределенной нагрузкой

На левой опоре возникают реакции – вертикальная сила $ql$ и момент $M = \frac<>><2>$.

$M(x) = — \frac<>> <2>+ ql \cdot x — \frac<>><2>$, дважды интегрируем

Так как в сечении $A$ (в защемлении) отсутствует прогиб и угол поворота, получим следующую систему уравнений

$\left\ < \beginEI\,y'(0) = F(\frac<<<0^2>>> <2>— l \cdot 0) + C = 0 \hfill \\ EI\,y(0) = F(\frac<<<0^3>>> <6>— l\frac<<<0^2>>><2>) + C \cdot 0 + D = 0. \hfill \\ \end \right.$

Решение системы уравнений приводит к результату $C = 0$, $D = 0$.

Окончательно функция прогибов для рассматриваемой балки имеет вид

Максимальный прогиб будет иметь место при $x = l$

Максимальный угол поворота сечения также будет иметь место при $x = l$