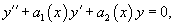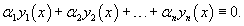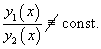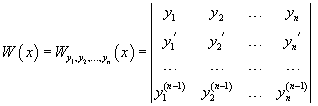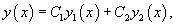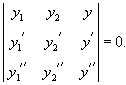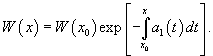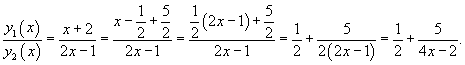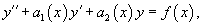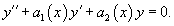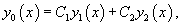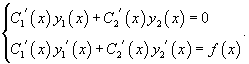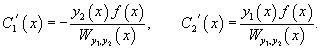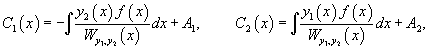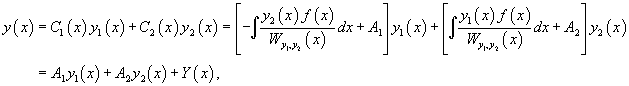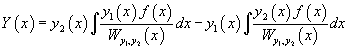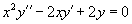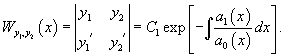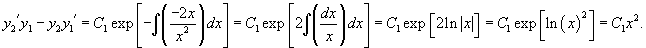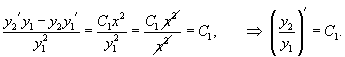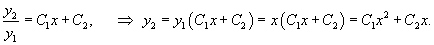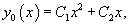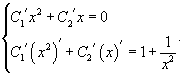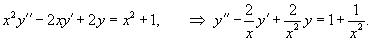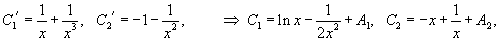Интегрируемые уравнения второго порядка с переменными коэффициентами

Интегрируемые уравнения второго порядка с переменными коэффициентами

Если же это тождество выполняется лишь при , то указанные функции , , . называются линейно независимыми на отрезке .

Для случая двух функций критерий линейной независимости можно записать в более простом виде: Функции , будут линейно независимыми на отрезке , если их отношение на данном отрезке тождественно не равно постоянной:

В противном случае, при 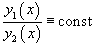, эти функции будут линейно зависимыми .

Пусть n функций , , . имеют производные порядка. Определитель

называется определителем Вронского или вронскианом для указанной системы функций.

Теорема . Если система функций , , . линейна зависима на отрезке , то ее определитель Вронского тождественно равен нулю на этом отрезке.

Отсюда следует, что если определитель отличен от нуля хотя бы в одной точке отрезка , то функции , , . будут линейно независимыми. Это свойство определителя Вронского позволяет выяснить, являются ли найденные решения однородного дифференциального уравнения линейно независимыми.

Совокупность двух линейно независимых частных решений линейного однородного дифференциального уравнения второго порядка образует его фундаментальную систему решений .

Если , − фундаментальная система решений, то общее решение уравнения второго порядка представляется в виде

где , − произвольные постоянные.

Заметим, что по заданной фундаментальной системе решений , можно построить соответствующее однородное дифференциальное уравнение. Для случая второго порядка такое уравнение выражается через определитель в виде:

Итак, как указано выше, общее решение однородного дифференциального уравнения второго порядка является линейной комбинацией двух линейно независимых частных решений , этого уравнения.

Очевидно, что частные решения зависят от коэффициентов дифференциального уравнения. Формула Лиувилля-Остроградского устанавливает связь между вронскианом , построенном на базе частных решений , , и коэффициентом в дифференциальном уравнении.

Пусть − определитель Вронского решений , линейного однородного дифференциального уравнения 2-го порядка

К сожалению, общего метода отыскания частного решения не существует. Обычно это можно сделать путем подбора.

Если известно частное решение линейного однородного уравнения второго порядка, то его можно преобразовать к линейному уравнению первого порядка с помощью подстановки и последующей замены .

Другой способ понижения порядка основан на использовании формулы Лиувилля-Остроградского. Здесь также одно частное решение должно быть известно. Соответствующие примеры разобраны ниже.

где , и − непрерывные функции на отрезке .

Соответствующее однородное уравнение записывается в виде

Метод вариации постоянных (или метод Лагранжа) используется для построения общего решения неоднородного уравнения, когда известно общее решение ассоциированного с ним однородного уравнения.

Пусть общее решение однородного уравнения 2-го порядка выражается через фундаментальную систему решений и :

где C₁, C₂ − произвольные постоянные. Идея данного метода состоит в том, что вместо постоянных C₁ и C₂рассматриваются функции и , которые подбираются таким образом, чтобы решение удовлетворяло неоднородному уравнению.

Производные неизвестных функций и можно определить из системы уравнений

Применяя метод вариации параметров, важно помнить, что функция должна соответствовать дифференциальному уравнению, приведенному к стандартному виду, т.е. коэффициент перед старшей производной должен быть равен 1.

Далее, зная производные и , можно найти и сами функции и :

Тогда общее решение исходного неоднородного уравнения будет выражаться формулой

Теперь воспользуемся методом вариации постоянных и построим общее решение неоднородного уравнения. Будем рассматривать параметры C₁ и C₂ как функции от переменной x. Производные этих функций определяются из системы уравнений

В результате получаем общее решение неоднородного уравнения в виде

ЛДУ с переменными коэффициентами. Метод Лагранжа

Линейные дифференциальные уравнения с переменные коэффициентами

Если известно частное решение уравнения

то его порядок можно понизить на единицу (не нарушая линейности уравнения), полагая , где — новая неизвестная функция, а затем делая замену (можно непосредственно делать замену ).

Если известно частных линейно независимых решений уравнения (32), то порядок уравнения может быть понижен на единиц.

Общее решение уравнения

есть сумма какого-нибудь его частного решения и общего решения соответствующего однородного уравнения (32).

Если известна фундаментальная система соответствующего однородного уравнения (32), то общее решение неоднородного уравнения (33) может быть найдено методом вариации постоянных ( метод Лагранжа ).

Общее решение уравнения (32) имеет вид

где — произвольные постоянные.

Будем искать решение уравнения (33) в виде

где — некоторые пока неизвестные функции от . Для их определения получаем систему

Разрешая эту систему относительно , получаем

где — произвольные постоянные. Внося найденные значения в (34), получаем общее решения уравнения (33).

В частности, для уравнения второго порядка

Решая (36) относительно и , получаем

где и — постоянные интегрирования.

Замечание. Для уравнения , где , система (36) будет выглядеть так:

Пример 1. Найти общее решение уравнения , если есть его частное решение.

Решение. Положим , где — новая неизвестная функция от , тогда

Подставляя в данное уравнение, получаем

Но так как есть частное решение данного уравнения, то , поэтому имеем

Но , а значит , и уравнение (37) примет вид

Перепишем его в виде . Отсюда имеем , откуда

Интегрируя это уравнение, найдем и, следовательно, общее решение данного уравнения будет

Пример 2. Найти общее решение уравнения .

Решение. Общее решение соответствующего однородного уравнения имеет вид (см. пример 1)

и следовательно, его фундаментальная система решений будет

Будем искать общее решение данного уравнения методом вариации произвольных постоянных:

где — постоянные неизвестные функции от , подлежащие определению. Для их нахождения составим следующую систему:

Отсюда находим: . Интегрируя, получаем

Подставляя эти значения и в выражение для , найдем общее решение данного уравнения

Пример 3. Решить уравнение .

Решение. Соответствующее однородное уравнение будет . Его характеристическое уравнение имеет мнимые корни , и общее решение однородного уравнения имеет вид

Общее решение исходного уравнения ищем в виде

где и — неизвестные функции от . Для их нахождения составим систему

Разрешаем эту систему относительно и :

Подставляя выражения и в (38), получаем общее решение данного уравнения

Здесь есть частное решение исходного неоднородного уравнения.

Пример 4. Зная фундаментальную систему решений соответствующего однородного уравнения, найти частное решение уравнения

Решение. Применяя метод вариации постоянных, находим общее решение уравнения (39):

При первые два слагаемых правой части (40) стремятся к бесконечности, причем при любых , неравных нулю одновременно, функция есть бесконечно большая функция при . Третье слагаемое правой части (40) имеет пределом ноль при , что легко установить с помощью правила Лопиталя. Таким образом, функция , которая получается из (40) при и , будет решением уравнения (39), удовлетворяющим условию .

Составление дифференциального уравнения по заданной фундаментальной системе решений

Рассмотрим линейно независимую на отрезке систему функций

имеющих все производные до n-го порядка включительно. Тогда уравнение

где — неизвестная функция, будет линейным дифференциальным уравнением, для которого, как нетрудно видеть, функции составляют фундаментальную систему решений. Коэффициент при в (42) есть определитель Вронского системы (41). Те точки, в которых этот определитель обращается в ноль, будут особыми точками построенного уравнения — в этих точках обращается в ноль коэффициент при старшей производной .

Пример 1. Составить дифференциальное уравнение, для которого образуют фундаментальную систему решений.

Решение. Применяя формулу (42), получаем

Раскрывая определитель в левой части (43) по элементам третьего столбца, будем иметь . Это и есть искомое дифференциальное уравнение.

Пример 2. Составить дифференциальное уравнение, для которого функции фундаментальную систему решений образуют функции .

Решение. Составим уравнение вида (42):

Раскрывая последний определитель по элементам 3-го столбца, будем иметь

В этом примере определитель Вронского обращается в ноль при . Это не противоречит общей теории, в силу которой определитель Вронского фундаментальной системы решений линейного однородного дифференциального уравнения

с непрерывными на отрезке коэффициентами не обращается в ноль ни в одной точке отрезка . Записав уравнение (44) в виде

видим, что коэффициент при терпит разрыв при , так что в точке непрерывность коэффициентов уравнения (45) нарушается.

Разные задачи

Пусть — фундаментальная система линейного однородного уравнения

Тогда имеет место формула Остроградского–Лиувилля

где — определитель Вронского, а — любое значение из отрезка , на котором непрерывны коэффициенты уравнения.

Пример 1. Показать, что линейное дифференциальное уравнение имеет решение вида , где — некоторый многочлен. Показать, что второе решение этого уравнения имеет вид , где — также многочлен.

Решение. Будем искать решение в виде многочлена, например, первой степени: . Подставляя в уравнение, найдем, что . Пусть , тогда ;. таким образом, многочлен будет решением данного уравнения. Перепишем данное уравнение в виде

Пусть — второе частное решение данного уравнения, линейно независимое с первым. Находим определитель Вронского системы решений

здесь . Применяя формулу Остроградского–Лиувилля, будем иметь

где — любое значение , причем , или ; здесь . Для нахождения получили линейное дифференциальное уравнение первого порядка. Деля обе части этого уравнения на , приведем его к виду

Интегрируемые уравнения второго порядка с переменными коэффициентами

Линейным называется дифференциальное уравнение n -го порядка , если оно 1-ой степени относительно искомой функции y ( x ) и ее производных , то есть имеет вид:

Если коэффициент P ₀ ( x ) ≠ 1, то на него можно поделить и после соответствующих переобозначений получить:

Уравнение (8.43) называется уравнением с переменными коэффициентами. Предположим, что в нем функции , непрерывны на интервале . Тогда для уравнения (8.43) на данном интервале имеет место задача Коши, сформулированная нами ранее.

Примечание. Частным случаем (8.43) является линейное дифференциальное уравнение 2-го порядка с переменными коэффициентами:

Если в уравнении (8.43) f ( x ) ≡ 0, то оно называется однородным, если f ( x ) ≠ 0, то неоднородным.

Теорема 8.3 (о структуре общего решения линейного неоднородного ДУ). Общее решение линейного неоднородного дифференциального уравнения представляет собой сумму общего решения соответствующего однородного и некоторого частного решения неоднородного уравнения . Запишем коротко:

Однородное дифференциальное уравнение, соответствующее неоднородному уравнению (8.43), имеет вид:

Пусть в уравнении (8.45) функции . Тогда оно принимает вид:

и называется линейным однородным дифференциальным уравнением n -го порядка с постоянными коэффициентами , где – функции, n раз дифференцируемые.

Рассмотрим решения уравнений (8.45) и (8.46). Обозначим полную совокупность их линейно независимых решений через . Тогда, по свойству решений однородного уравнения, их линейная комбинация также является решением уравнения (8.45) и (8.46), т о есть общее решение может быть записано в виде:

где c_i – константы интегрирования.

Перейдем к конструированию функций . Какого они вида? Так как эти функции в уравнениях (8.45) и (8.46) n раз дифференцируемы, то их конструкция при дифференцировании не меняется. Это возможно в случае экспоненциального вида функций, то есть при

где , . Отсюда, линейная комбинация функций (8.48):

– также решение уравнений (8.45) и (8.46).

Рассмотрим одну из функций (8.48) – функцию y = e λx как решение для уравнения (8.46) с постоянными коэффициентами. Продифференцируем ее n раз:

Так как e λx ≠ 0 , то ( 8.50)

–алгебраическое уравнение n -ой степени относительно λ, называемое характеристическим уравнением для уравнения (8.46). Известно, что уравнение n -ой степени имеет равно n корней как действительных, так и комплексных, с учетом их кратности. Значит, характеристическое уравнение (8.50) дает нам n значений числа λ, ранее обозначенных нами через , которые при подстановке в (8.49) приводит нас к окончательному виду общего решения линейного однородного дифференциального уравнения (8.46) с постоянными коэффициентами.

Рассмотрим наиболее распространенный частный случай уравнения (8.46) – его аналог 2-го порядка:

Для данного уравнения характеристическое уравнение (8.50) принимает вид:

Уравнение (8.52) является квадратным относительно λ. В зависимости от дискриминанта D характеристического уравнения рассматривают три случая, приведенных в таблице 8.1.

Пример 8.17. Найти общее решение уравнений:

а) Составляем характеристическое уравнение λ 2 +2 λ – 15 = 0. Корнями этого уравнения будут λ ₁ = –5 и λ ₂ = 3 . Тогда, применяя (8.53), получаем общее решение: y=C ₁ e – 5x +C ₂ e 3x .

б) Составляем характеристическое уравнение λ 2 – 16 λ + 64 = 0.

Решая это уравнение, получим λ ₁ = λ ₂ = 8 . Так как корни равные, то, применяя (8.54), будем иметь:

в) Характеристическое уравнение λ 2 – 4 λ + 13 = 0 имеет комплексные корни λ ₁ = 2+3 i и λ ₂ = 2 –3 i . Положив в (8.55) α=2 и β = 3, получим общее решение: .

г) Характеристическое уравнение λ 2 +9 = 0 имеет корни λ 1;2 = ± 3 i . П олагая в (8.55) α=0 и β = 3, получим общее решение

Рассмотрим теперь линейное неоднородное дифференциальное уравнение 2-го порядка с постоянными коэффициентами:

Теорема 8.4. Пусть задано линейное дифференциальное неоднородное уравнение второго порядка с постоянными коэффициентами и п равой частью специального вида

1. Если не является корнем характеристического уравнения соответствующего однородного уравнения, то частное решение уравнения (8.57) имеет вид:

где – многочлены общего вида (с неопределенными коэффициентами).

2. Если – корень характеристического уравнения кратности s , то частное решение уравнения (8.57) имеет вид:

– многочлены общего вида

Рассмотрим в таблице 8.2 некоторые случаи составления частного решения линейного неоднородного дифференциального уравнения (8.57) по специальному виду его правой части.

Пример 8.18. Найти общее решение уравнения .

Решение. Найдем общее решение соответствующего однородного ДУ: . Х арактеристическое уравнение λ 2 +2 λ +1 = 0 имеет корень λ₁ = 1 кратности 2 (смотри таблицу 8.1). Значит, y_{o . o .} = c ₁ ∙ e x + c ₂ ∙ x ∙ e x . Находим частное решение исходного уравнения. В нем правая часть x –4=( x –4)∙ e 0∙ x есть формула вида P ₁ ( x )∙ e 0∙ x , причем α= 0 не является корнем характеристического уравнения: α ≠ λ . Поэтому согласно формуле (8.58), частное решение y _ч.н. ищем в виде y _ч.н. = Q ₁ ( x )∙ e 0∙ x , т.е. y _ч.н. = Ax + B , где A и B – неопределенные коэффициенты. Тогда

Пример 8.19. Решить уравнение .

уравнения . Характеристическое уравнение λ 2 – 4 λ +13 = 0 имеет корни λ₁ = 2+3 i , λ 2 = 2 –3 i (смотри таблицу 8.1). Следовательно, .

Находим частное решение y _ч.н. . Правая часть неоднородного уравнения в нашем случае имеет вид

Отсюда, сравнивая коэффициенты при косинусе и синусе, имеем . Следовательно, A = 1, B = – 3 . Поэтому . И наконец, с учетом теоремы 8.3 получаем общее решение заданного линейного неоднородного ДУ в виде:

Пример 8.20. Найти частное решение уравнения , удовлетворяющее начальным условиям .

Решение . Находим общее решение однородного уравнения . Характеристическое уравнение λ 2 – λ – 2 = 0 имеет два корня λ ₁ = –1 и λ ₂ = 2 (смотри таблицу 8.1) ; тогда y_{o . o .} = C ₁ ∙ e – x + C ₂ ∙ e 2 x – общее решение соответствующего однородного ДУ.

В правой части заданного уравнения имеется показательная функция. Так как в данном случае α=2 совпадает с одним из корней характеристического уравнения, то частное решение следует искать в виде функции Axe 2 x . Таким образом, y _ч.н. = Axe 2 x . Дифференцируя дважды это равенство, по лучим: . Подставим y _ч.н. и ее производные в левую часть заданного уравнения и найдем коэффициент A : . Следовательно, частное решение y _ч.н. = 3xe 2 x , общее решение

Используя начальные условия, определим значения произвольных постоянных C ₁ и C ₂ . Дифференцируя общее решение (8.60), получим:

Подставим в общее решение (8.60) значения x = 0 и y = 2, будем иметь 2 = C ₁ + C ₂ . Подставим в выражение для значения x = 0 и , будем иметь: 13 = – C 1 +2 C 2 +3 ; 10 = – C 1 + C 2 . Из этих уравнений составим систему , из которой находим: C 1 = – 2 и C 2 =4 . Таким образом, есть то частное решение, которое удовлетворяет заданным начальным условиям

Теорема 8.5 (о наложении решений). Если правая часть уравнения (8.56) представляет собой сумму двух функций: , а y _{1 ч.н.} и y _{2 ч.н.} – частные решения уравнений и соответственно, то функция

является частным решением данного уравнения