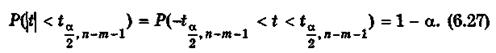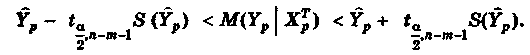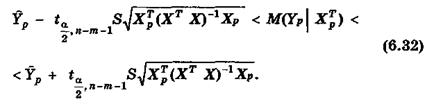Интервальные оценки для коэффициентов линейного уравнения

Интервальные оценка коэффициентов регрессии

ЛЕКЦИЯ 5

Анализ точности оценки коэффициентов регрессии. Стандартные ошибки регрессии и коэффициентов регрессии. Проверка гипотез относительно коэффициентов регрессии. Интервальные оценки коэффициентов регрессии. Показатели качества уравнения регрессии. Коэффициент детерминации. Критерий Фишера. Интервалы прогноза по уравнению регрессии.

§5.2. АНАЛИЗ ТОЧНОСТИ ОЦЕНОК КОЭФФИЦИЕНТОВ
РЕГРЕССИИ

5.2.1. Оценка дисперсии случайного отклонения s 2

Проведем статистический анализ построенного уравнения регрессии, т.е. выясним насколько надёжны полученные оценки коэффициентов регрессии; как хорошо полученное уравнение регрессии описываем имеющиеся статистические данные, может быть следует изменить спецификацию модели; оценить точность прогноза, т.е. построить доверительный интервал для зависимой переменной. Для того чтобы провести такой статистический анализ модели, нужно, как мы видели в предыдущей лекции, знать закон распределения случайной величины e. При построении уравнения регрессии МНК такой информации не требовалось (в этом одно из преимуществ МНК), однако для проведения статистического анализа такая информация востребована. В дальнейшем мы будем работать в рамках нормальной классической регрессионной модели, т.е. выполняются все условия Гаусса-Маркова и, в частности, e подчиняется нормальному закону распределения. Вообще говоря, выполнимость этих условий ещё надо проверить, в данной лекции мы будем предполагать, что эти условия априори выполняются.

Сформулированные выше статистические свойства МНК-оценок коэффициентов регрессии справедливы и без предположения о нормальности случайного отклонения e. Однако, даже располагая информацией о состоятельности, несмещённости и оптимальности оценок, мы не можем решить задачи о построении доверительных интервалов для истинных значений рассматриваемых параметров, так же как и для неизвестных значений функции регрессии. Необходимой базой для решения этих задач является знание законов распределения вероятностей используемых оценок. Именно в рамках нормальной классической линейной регрессионной модели можно решить вопросы о значимости коэффициентов регрессии и построении для них доверительных интервалов, о качестве построенного уравнения регрессии в целом, о точности прогноза по этому уравнению.

В силу того, что случайные отклонения e_i по выборке определены быть не могут, при анализе надежности оценок коэффициентов регрессии они заменяются отклонениями значений y_i переменной Y от оцененной линии регрессии. Не следует путать эмпирические отклонения e_i с теоретическими отклонениями e_i. И те и другие являются случайными величинами, однако разница состоит в том, что эмпирические отклонения, в отличие от теоретических, наблюдаемы.

Кажется вполне естественной гипотеза, что оценка s 2 связана с суммой квадратов остатков регрессии . В самом деле,

,

где , . Тогда

Вычислим математическое ожидание .

.

Используя соотношение , получаем

,

.

.

Отсюда следует, что

. (5.34)

является несмещенной оценкой дисперсии случайного отклонения s 2 . Отметим, что S называется стандартной ошибкой регрессии,

Отметим, что в математической статистике для получения несмещенной оценки дисперсии случайной величины соответствующую сумму квадратов отклонений от средней делят не на число наблюдений n, на число степеней свободы n–m, равное разности между числом независимых наблюдений случайной величины n и числом связей, ограничивающих свободу их измерения, т.е. число m уравнений, связывающих эти наблюдения. Поэтому в знаменателе выражения (5.34) стоит число степеней свободы n–2, т.к. две степени свободы теряются при определении двух параметров прямой из системы нормальных уравнений.

5.2.2.Проверка гипотез относительно коэффициентов
регрессии

Эмпирическое уравнение регрессии определяется на основе конечного числа статистических данных. Поэтому коэффициенты эмпирического уравнения регрессии являются случайными величинами, изменяющимися от выборки к выборке. Наиболее важной на начальном этапе статистического анализа построенной модели является задача установления значимости коэффициентов регрессии. Данный анализ осуществляется по схеме статистической проверки гипотез.

Можно показать, что в случае классической нормальной линейной регрессионной модели оценка дисперсии S 2 случайных отклонений является независимой от b₀ и b₁ случайной величиной. Это позволяет построить статистики для проверки статистических гипотез.

В предыдущей лекции мы получили дисперсии оценок b₀ и b₁ коэффициентов регрессии в том случае, если s 2 известно. На практике, как правило, дисперсия отклонений s 2 неизвестна и оценивается по наблюдениям одновременно с коэффициентами регрессии b₀ и b₁. В этом случае вместо дисперсий оценок b₀ и b₁ мы можем получить лишь оценки дисперсий b₀ и b₁, заменив s 2 на S 2 . Тогда

, (5.35)

, (5.36)

. (5.37)

Величины и называются стандартными ошибками коэффициентов регрессии коэффициентов b₀ и b₁, соответственно.

, (5.38)

которая при справедливости H₀ имеет распределение Стьюдента с числом степеней свободы k=n–2. Следовательно, H₀ отклоняется на основании данного критерия, если

, (5.39)

где a – требуемый уровень значимости. При невыполнении (5.39) считается, что нет оснований для отклонения H₀.

Наиболее важной на начальном этапе статистического анализа построенной модели является проверка гипотезы H₀:b₁=0 при альтернативной гипотезе H₁:b₁¹0. Гипотеза в такой постановке называется гипотезой о статистической значимости коэффициента регрессии. При этом, если гипотеза H₀ принимается, то есть все основания считать, что величина Y не зависит от X. В этом случае говорят, что коэффициент b₁ статистически незначим. При отклонении гипотезы H₀ коэффициент b₁ считается статистически значимым, что указывает на наличие линейной зависимости между Y и X. В данном случае рассматривается двусторонняя критическая область, т.к. важным является именно отличие от нуля коэффициента регрессии, а он может быть как положительным, так и отрицательным.

Поскольку полагается, b₁=0, то формальная значимость оцененного коэффициента регрессии b₁ проверяется при помощи критерия

, (5.40)

который называется t-статистикой (t-тестом).

По аналогичной схеме на основе t-статистики проверяется гипотеза о статистической значимости коэффициента b₀:

. (5.41)

Отметим, что для парной регрессии более важным является анализ статистической значимости коэффициента b₁, т.к. именно в нем скрыто влияние объясняющей переменной X на зависимую переменную Y.

Отметим также, что значения критериев (5.40) и (5.41) приводят всеми компьютерными пакетами в результатах регрессии. В учебниках и монографиях по эконометрике наблюдаемые значения t-критерия Стьюдента (или стандартные ошибки) указываются вместе с уравнением регрессии под соответствующим коэффициентом:

или .

Пример 5.3. Проверить значимость коэффициентов регрессии, полученных в
примере 5.1 (см. лекцию 4).

Решение. По данным таблицы 5.2 найдем оценку дисперсии случайного отклонения, т.е. квадрат стандартной ошибки регрессии:

.

и .

Следовательно, наблюдаемое значение t-критерия Стьюдента коэффициента b₁ равно

.

Критическое значение t-критерия Стьюдента на уровне значимости a=0,05 равно

.

Поскольку , то нулевая гипотеза отвергается в пользу альтернативной при выбранном уровне значимости. Это подтверждает статистическую значимость коэффициента регрессии b₁.

Аналогично проверяется статистическая значимость коэффициента b₀:

и .

Тогда наблюдаемое значение t-критерия Стьюдента коэффициента b₀ будет равно

.

Поскольку , то нет оснований отклонять гипотезу о статистической незначимости коэффициента b₀.

Таким образом, результаты анализа можно представить в виде

или . â

Интервальные оценка коэффициентов регрессии

Предположение о нормальном распределении случайных отклонений e_i с нулевым математическим ожиданием и постоянной дисперсией, т.е. , позволяет получать не только наилучшие линейные несмещенные точечные оценки (BLUE-оценки) b₀ и b₁ коэффициентов b₀ и b₁ коэффициентов линейного уравнения регрессии, но и находить их интервальные оценки.

Здесь исходят из того, что случайные величины b₀ и b₁ при указанных выше предположениях имеют нормальные распределения:

, .

и

будут иметь стандартное нормальное распределение. Однако в выражениях для b₀ и b₁ дисперсия заменяется ее оценкой S 2 . Поэтому выражения

и (5.42)

будут иметь t-распределение Стьюдента с k=n–2 степенями свободы.

Для построения доверительных интервалов с помощью таблиц критических точек распределения Стьюдента по доверительной вероятности g=1–a и числу степеней свободы k=n–2 определяют критическое значение , удовлетворяющее условию

. (5.43)

Подставив сюда каждую из формул (5.36), получим

; .

После преобразований выражений, стоящих в скобках, имеем:

,

.

Таким образом, доверительные интервалы для коэффициентов регрессии будут иметь следующий вид

, , (5.44)

которые с вероятностью g=1–a накрывают определяемые параметры b₀ и b₁.

Пример 5.4. Найти интервальные оценки для примера 5.1, 5.3 с уровнем надёжности a=0,05.

Решение. В примерах 5.1-5.2 было найдено:

, , , , .

Тогда по формулам (5.46) находим для коэффициента b₀:

; .

Таким образом, с вероятностью 0,95 коэффициент регрессии b₀ принимает значения из интервала . Поскольку ноль также попадает в этот интервал, то, как и следовало ожидать, коэффициент b₀ не является значимым.

Для коэффициента b₁ получаем следующие результаты:

; .

Таким образом, с вероятностью 0,95 коэффициент регрессии b₁ принимает значения из интервала . Поскольку D₁ значительно меньше b₁, то точность прогноза, связанного с этим коэффициентом будет достаточно высокой. â

Интервальные оценки коэффициентов регрессии

По аналогии с парной регрессией после опре­деления точечных оценок коэффициентов — (j =0,1,…,m) теоретического уравнения регрессии могут быть рассчитаны ин­тервальные оценки указанных коэффициентов. Для построения интервальной оценки коэффициента строится -статистика

(6.26)

имеющая распределение Стюдента с числом степеней свободы v= n — т — 1 (n— объем выборки, т — количество объясняю­щих переменных в модели)

Пусть необходимо построить 100(1 — )%-й доверительный интервал для коэффициента Тогда по таблице критических точек распределения Стьюдента по требуемому уровню значи­мости а и числу степеней свободы находят критическую точку Удовлетворяющую условию

Подставляя (6.26) в (6.27), получаем

или после преобразования

Напомним, что 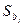рассчитывается по формуле

Таким образом, доверительный интервал, накрывающий с надежностью (1 – ) неизвестное значение параметра , опре­деляется неравенством

Отметим, что по аналогии с парной регрессией (может быть построена интервальная оценки для среднего значения предсказания:

В матричной форме это неравенство имеет вид:

17)Коэффициент детерминации R 2 . Отличие скорректированного коэффициента детерминации от обычного.

После проверки значимости каждого коэффициента регрес­сии обычно проверяется общее качество уравнения регрессии. Для этой цели, как и в случае парной регрессии, используется

коэффициент детерминации R , который в общем случае рас­считывается по формуле

Как отмеча­лось, в общем случае . Чем ближе этот коэффициент к единице, тем больше уравнение регрессии объясняет поведение У. Поэтому естественно желание построить регрессию с наи­большим R 2 .

Для множественной регрессии коэффициент детерминации является неубывающей функцией числа объясняющих пере­менных. Добавление новой объясняющей переменной никогда не уменьшает значение R 2 . Действительно, каждая следующая объясняющая переменная может лишь дополнить, но никак не сократить информацию, объясняющую поведение зависимой переменной. Это уменьшает (в худшем случае не увеличивает) область неопределенности в поведении У.

Иногда при расчете коэффициента детерминации для полу­чения несмещенных оценок в числителе и знаменателе вычи­таемой из единицы дроби делается поправка на число степеней свободы. Вводится так называемый скорректированный (ис­правленный) коэффициент детерминации:

(6.35)

Можно заметить, что является несмещенной оценкой общей дисперсии — дисперсии отклонений значений переменной У от . При этом число ее степеней сво­боды равно (n — 1). Одна степень свободы теряется при вычис­лении .

В свою очередь является несмещенной оцен­кой остаточной дисперсии — дисперсии случайных отклонений (отклонений точек наблюдений от линии регрессии). Ее число степеней свободы равно (n — m -1). Потеря (m + 1) степени свобо­ды связана с необходимостью решения системы (m + 1) линейно­го уравнения при определении коэффициентов эмпирического уравнения регрессии. Попутно заметим, что несмещенная оцен­ка объясненной дисперсии (дисперсии отклонений точек на ли­нии регрессии от ) имеет число степеней свободы, равное разно­сти степеней свободы общей дисперсии и остаточной дисперсии (n — 1) — (n- m -1) = m.

Соотношение (6.35) может быть представлено в следую­щем виде:

(6.36)

Из (6.36) очевидно, что 2 для m > 1. С ростом значения m скорректированный коэффициент детерминации рас­тет медленнее, чем (обычный) коэффициент детерминации R 2 . Другими словами, он корректируется в сторону уменьшения с ростом числа объясняющих переменных. Нетрудно заметить, что = R 2 только при R 2 = 1. может принимать отрица­тельные значения (например, при R 2 = 0).

Доказано, что R увеличивается при добавлении новой объ­ясняющей переменной тогда и только тогда, когда t-статистика для этой переменной по модулю больше единицы. Поэтому до­бавление в модель новых объясняющих переменных осуществ­ляется до тех пор, пока растет скорректированный коэффици­ент детерминации.

Обычно приводятся данные как по R 2 , так и по , яв­ляющиеся суммарными мерами общего качества уравнения регрессии. Однако не следует абсолютизировать значимость коэффициентов детерминации. Существует достаточно приме­ров неправильно специфицированных моделей, имеющих высо­кие коэффициенты детерминации (обсудим данную ситуацию позже). Поэтому коэффициент детерминации в настоящее вре­мя рассматривается лишь как один из ряда показателей, кото­рый нужно проанализировать, чтобы уточнить строящуюся модель.

18)Анализ статистической значимости коэффициента детерминации R 2 .

на практике чаще вместо указанной гипотезы про­веряют тесно связанную с ней гипотезу о статистической значи­мости коэффициента детерминации R 2 :

Для проверки данной гипотезы используется следующая F-статистика:

(6.38)

Величина F при выполнении предпосылок МНК и при спра­ведливости Но имеет распределение Фишера, аналогичное рас­пределению F-статистики (6.37). Действительно, разделив чис­литель и знаменатель дроби в (6.37) на общую сумму квадратов отклонений , мы получим формулу(6.38);

Из (6.38) очевидно, что показатели F и R 2 равны или не равны нулю одновременно. Если F = 0, то R 2 = 0, и линия регрессии Y = является наилучшей по МНК, и, следова­тельно, величина Y линейно не зависит от .Для проверки нулевой гипотезы при заданном уровне значимости по таблицам критических точек распределения Фишера находится критическое значение . Нуле­вая гипотеза отклоняется, если F_набл > F_кр, Это равносильно тому, что R 2 > 0, т.е. R статистически значим.

Анализ статистики F позволяет сделать вывод о том, что для принятия гипотезы об одновременном равенстве нулю всех коэффициентов линейной регрессии коэффициент детермина­ции R 2 не должен существенно отличаться от нуля. Его критическое значение уменьшается при росте числа наблюдений и может стать сколь угодно малым.

Пусть, например, при оценке регрессии с двумя объясняющими переменными по 30 наблюдениям R 2 = 0,65. Тогда F_набл= .

По таблицам критических точек распределения Фишера найдем . =3,36; = 5,49. = 25,07 > F_кр как при 5% -м, так и при 1%-м уровне значимости, то нулевая гипотеза в обоих случаях отклоняется.

Если в той же ситуации , то . Предположение о незначимости связи отвергается и здесь.

Отметим, что в случае парной регрессии проверка нулевой гипо­тезы для F-статистики равносильна проверке нулевой гипотезы для t-статистики коэффициента корреляции.

В этом случае F-статистика равна квадрату t-статистики. Самостоятельную значимость коэффициент R 2 приобретает в случае множественной линейной регрессии.

§ 6. Интервальные оценки коэффициентов линейного уравнения регрессии

Базовыми предпосылками МНК является предположение о нормальном распределении отклонений еі с нулевым математическим ожиданием и постоянной дисперсией, т. е. е^Ф (0,о2).

Это позволяет получать не только наилучшие линейные несмещенные точечные оценки b0 и b1 коэффициентов во и в1 линейного уравнения регрессии, но и находить их интервальные оценки, что дает определенные гарантии точности.

Доверительные интервалы для коэффициентов имеют вид:

Фактически доверительный интервал определяет значения теоретических коэффициентов регрессии в0 и в1, которые будут приемлемыми с надежностью 1-а при найденных оценках b0 и b1.

Если обратиться к примеру 2.1, то 95%-е доверительные интервалы для коэффициентов будут следующими: