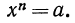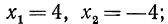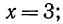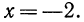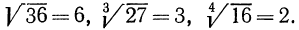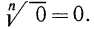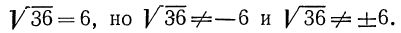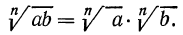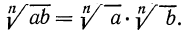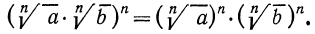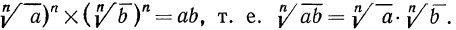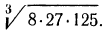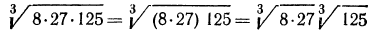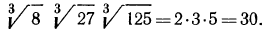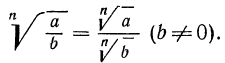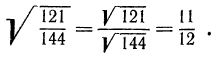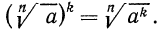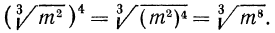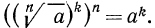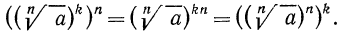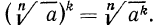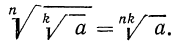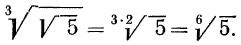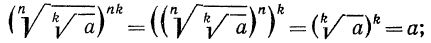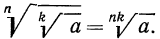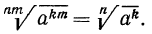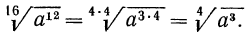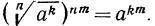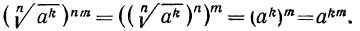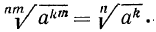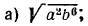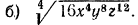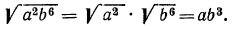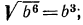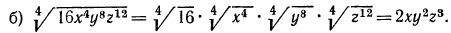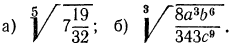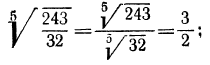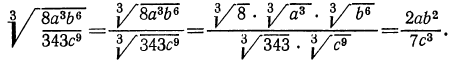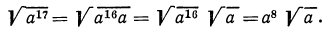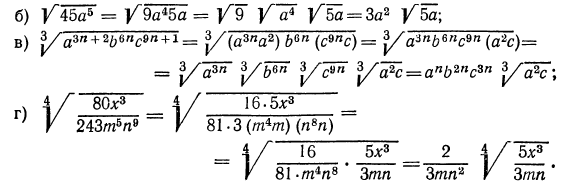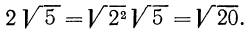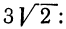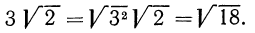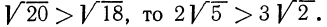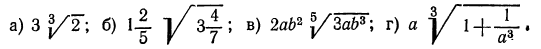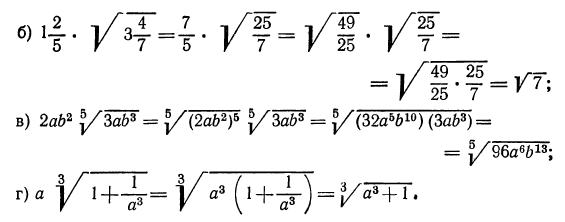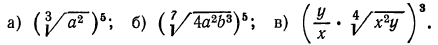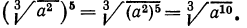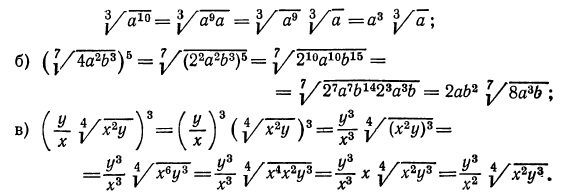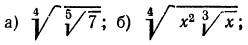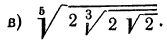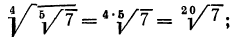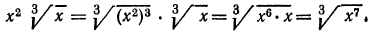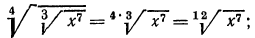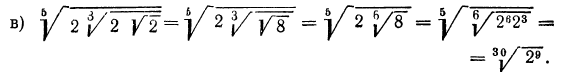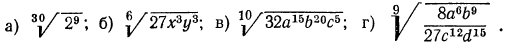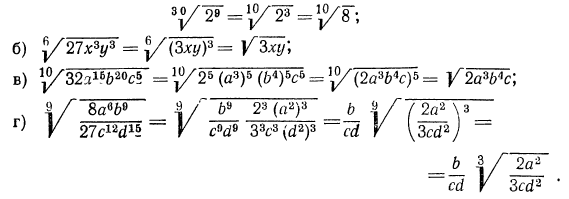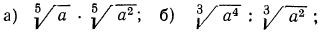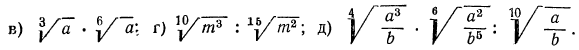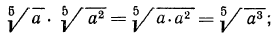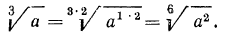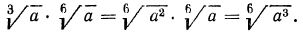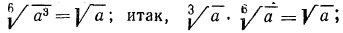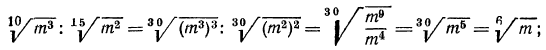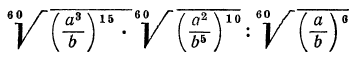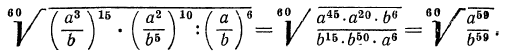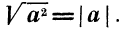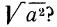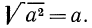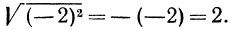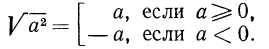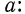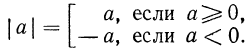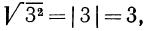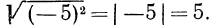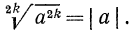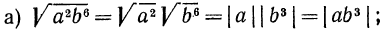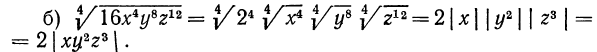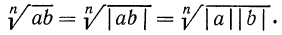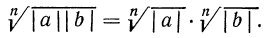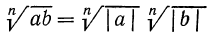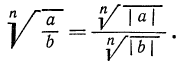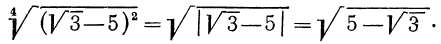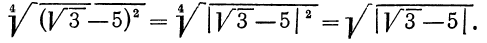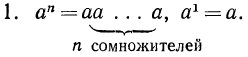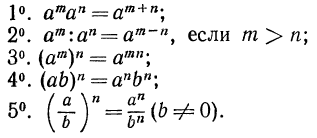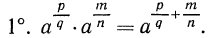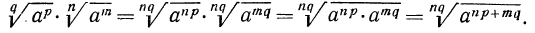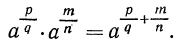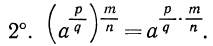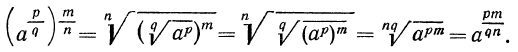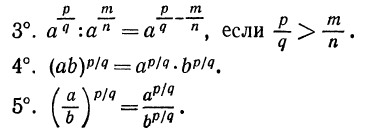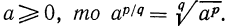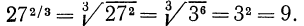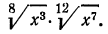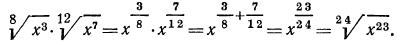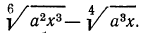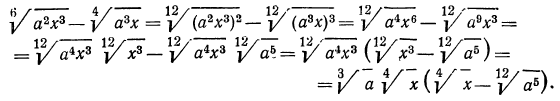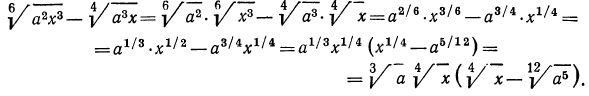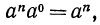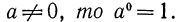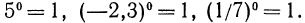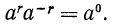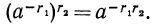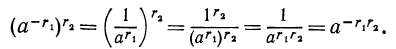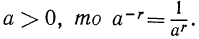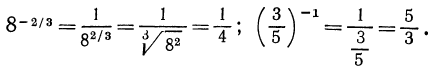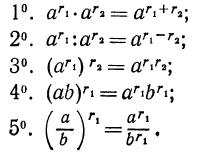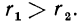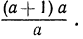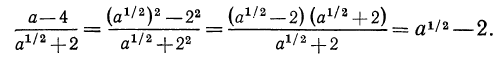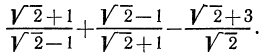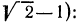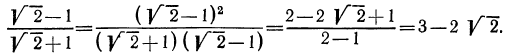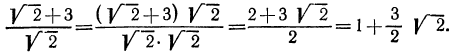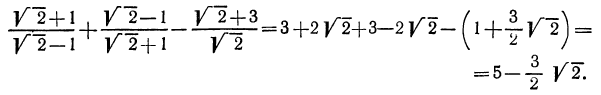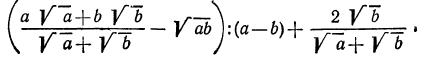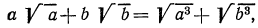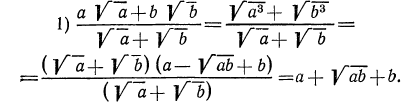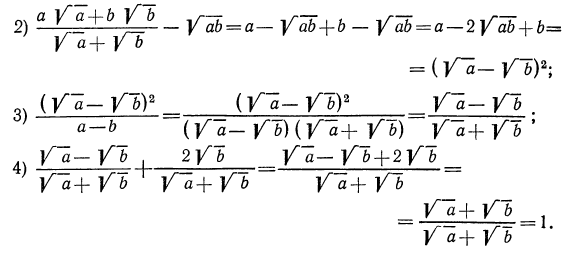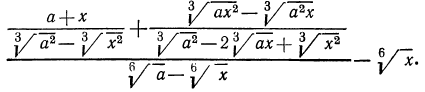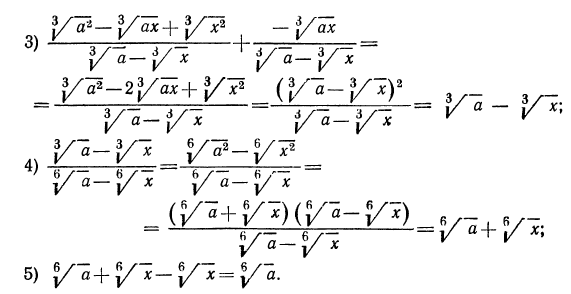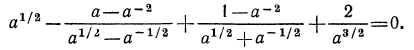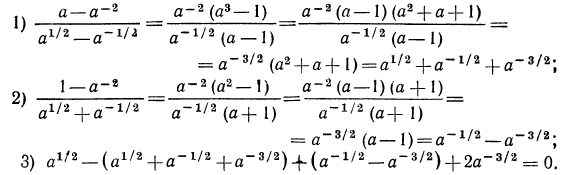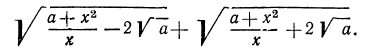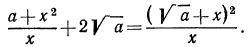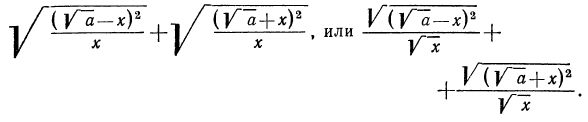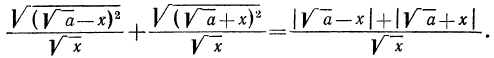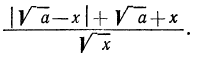Алгебра
План урока:
Иррациональные уравнения
Ранее мы рассматривали целые и дробно-рациональные уравнения. В них выражение с переменной НЕ могло находиться под знаком радикала, а также возводиться в дробную степень. Если же переменная оказывается под радикалом, то получается иррациональное уравнение.
Приведем примеры иррациональных ур-ний:
Заметим, что не всякое уравнение, содержащее радикалы, является иррациональным. В качестве примера можно привести
Это не иррациональное, а всего лишь квадратное ур-ние. Дело в том, что под знаком радикала стоит только число 5, а переменных там нет.
Простейшие иррациональные уравнения
Начнем рассматривать способы решения иррациональных уравнений. В простейшем случае в нем справа записано число, а вся левая часть находится под знаком радикала. Выглядит подобное ур-ние так:
где а – некоторое число (константа), f(x) – рациональное выражение.
Для его решения необходимо обе части возвести в степень n, тогда корень исчезнет:
Получаем рациональное ур-ние, решать которые мы уже умеем. Однако есть важное ограничение. Мы помним, что корень четной степени всегда равен положительному числу, и его нельзя извлекать из отрицательного числа. Поэтому, если в ур-нии
n – четное число, то необходимо, чтобы а было положительным. Если же оно отрицательное, то ур-ние не имеет корней. Но на нечетные n такое ограничение не распространяется.
Пример. Решите ур-ние
Решение. Справа стоит отрицательное число (– 6), но квадратный корень (если быть точными, то арифметический квадратный корень) не может быть отрицательным. Поэтому ур-ние корней не имеет.
Ответ: корней нет.
Пример. Решите ур-ние
Решение. Теперь справа стоит положительное число, значит, мы имеем право возвести обе части в квадрат. При этом корень слева исчезнет:
Пример. Решите ур-ние
Решение. Справа стоит отрицательное число, но это не является проблемой, ведь кубический корень может быть отрицательным. Возведем обе части в куб:
Конечно, под знаком корня может стоять и более сложное выражение, чем (х – 5).
Пример. Найдите решение ур-ния
Решение. Возведем обе части в пятую степень:
х 2 – 14х – 32 = 0
Получили квадратное ур-ние, которое можно решить с помощью дискриминанта:
D = b 2 – 4ac = (– 14) 2 – 4•1•(– 32) = 196 + 128 = 324
Итак, нашли два корня: (– 2) и 16.
Несколько более сложным является случай, когда справа стоит не постоянное число, а какое-то выражение с переменной g(x). Алгоритм решения тот же самый – необходимо возвести в степень ур-ние, чтобы избавиться от корня. Но, если степень корня четная, то необходимо проверить, что полученные корни ур-ния не обращают правую часть, то есть g(x), в отрицательное число. В противном случае их надо отбросить как посторонние корни.
Пример. Решите ур-ние
Решение. Возводим обе части во вторую степень:
х – 2 = х 2 – 8х + 16
D = b 2 – 4ac = (– 9) 2 – 4•1•18 = 81 – 72 = 9
Получили два корня, 3 и 6. Теперь проверим, во что они обращают правую часть исходного ур-ния (х – 4):
при х = 3 х – 4 = 3 – 4 = – 1
при х = 6 6 – 4 = 6 – 4 = 2
Корень х = 3 придется отбросить, так как он обратил правую часть в отрицательное число. В результате остается только х = 6.
Пример. Решите ур-ние
Решение. Здесь используется кубический корень, а потому возведем обе части в куб:
3х 2 + 6х – 25 = (1 – х) 3
3х 2 + 6х – 25 = 1 – 3х + 3х 2 – х 3
Получили кубическое ур-ние. Решить его можно методом подбора корня. Из всех делителей свободного коэффициента (– 26) только двойка обращает ур-ние в верное равенство:
Других корней нет. Это следует из того факта, что функция у = х 3 + 9х – 26 является монотонной.
Заметим, что если подставить х = 2 в левую часть исходного ур-ния 1 – х, то получится отрицательное число:
при х = 2 1 – х = 1 – 2 = – 1
Но означает ли это, что число 2 НЕ является корнем? Нет, ведь кубический корень вполне может быть и отрицательным (в отличие от квадратного). На всякий случай убедимся, что двойка – это действительно корень исходного уравнения:
Уравнения с двумя квадратными корнями
Ситуация осложняется, если в ур-нии есть сразу два квадратных корня. В этом случае их приходится убирать последовательно. Сначала мы переносим слагаемые через знак «=» таким образом, чтобы слева остался один из радикалов и ничего, кроме него. Возводя в квадрат такое ур-ние, мы избавимся от одного радикала, после чего мы получим более простое ур-ние. После получения всех корней надо проверить, какие из них являются посторонними. Для этого их надо просто подставить в исходное ур-ние.
Пример. Решите ур-ние
Решение. Перенесем вправо один из корней:
Возведем обе части в квадрат. Обратите внимание, что левый корень при этом исчезнет, а правый – сохранится:
Теперь снова перемещаем слагаемые так, чтобы в одной из частей не осталось ничего, кроме корня:
Снова возведем ур-ние в квадрат, чтобы избавиться и от второго корня:
(2х – 4) 2 = 13 – 3х
4х 2 – 16х + 16 = 13 – 3х
4х 2 – 13х + 3 = 0
D = b 2 – 4ac = (– 13) 2 – 4•4•3 = 169 –48 = 121
Имеем два корня: 3 и 0,25. Но вдруг среди них есть посторонние? Для проверки подставим их в исходное ур-ние. При х = 0,25 имеем:
Получилось ошибочное равенство, а это значит, что 0,25 не является корнем ур-ния. Далее проверим х = 3
На этот раз получилось справедливое равенство. Значит, тройка является корнем ур-ния.
Введение новых переменных
Предложенный метод последовательного исключения радикалов плохо работает в том случае, если корни не квадратные, а имеют другую степень. Рассмотрим ур-ние
Последовательно исключить корни, как в предыдущем примере, здесь не получится (попробуйте это сделать самостоятельно). Однако помочь может замена переменной.
Для начала перепишем ур-ние в более удобной форме, когда вместо корней используются степени:
х 1/2 – 10х 1/4 + 9 = 0
Теперь введем переменную t = x 1/4 . Тогда х 1/2 = (х 1/4 ) 2 = t 2 . Исходное ур-ние примет вид
Это квадратное ур-ние. Найдем его корни:
D = b 2 – 4ac = (– 10) 2 – 4•1•9 = 100 – 36 = 64
Получили два значения t. Произведем обратную замену:
х 1/4 = 1 или х 1/4 = 9
Возведем оба ур-ния в четвертую степень:
(х 1/4 ) 4 = 1 4 или (х 1/4 ) 4 = 3 4
х = 1 или х = 6561
Полученные числа необходимо подставить в исходное ур-ние и убедиться, что они не являются посторонними корнями:
В обоих случаях мы получили верное равенство 0 = 0, а потому оба числа, 1 и 6561, являются корнями ур-ния.
Пример. Решите ур-ние
х 1/3 + 5х 1/6 – 24 = 0
Решение. Произведем замену t = x 1/6 , тогда х 1/3 = (х 1/6 ) 2 = t 2 . Исходное ур-ние примет вид:
Его корни вычислим через дискриминант:
D = b 2 – 4ac = 5 2 – 4•1•(– 24) = 25 + 96 = 121
Далее проводим обратную заменуx 1/6 = t:
х 1/6 = – 8 или х 1/6 = 3
Первое ур-ние решений не имеет, а единственным решением второго ур-ния является х = 3 6 = 729. Если подставить это число в исходное ур-ние, то можно убедиться, что это не посторонний корень.
Замена иррационального уравнения системой
Иногда для избавления от радикалов можно вместо них ввести дополнительные переменные и вместо одного иррационального ур-ния получить сразу несколько целых, которые образуют систему. Это один из самых эффективных методов решения иррациональных уравнений.
Пример. Решите ур-ние
Решение. Заменим первый корень буквой u, а второй – буквой v:
Исходное ур-ние примет вид
Если возвести (1) и (2) в куб и квадрат соответственно (чтобы избавиться от корней), то получим:
Ур-ния (3), (4) и (5) образуют систему с тремя неизвестными, в которой уже нет радикалов:
Попытаемся ее решить. Сначала сложим (4) и (5), ведь это позволит избавиться от переменной х:
(х + 6) + (11 – х) = u 3 + v 2
из (3) можно получить, что v = 5 – u. Подставим это в (6) вместо v:
17 = u 3 + (5 – u) 2
17 = u 3 + u 2 – 10u + 25
u 3 + u 2 – 10u + 8 = 0
Получили кубическое ур-ние. Мы уже умеем решать их, подбирая корни. Не вдаваясь в подробности решения, укажем, что корнями этого ур-ния являются числа
подставим полученные значения в (4):
x + 6 = 1 3 или х + 6 = 2 3 или х + 6 = (– 4) 3
x + 6 = 1 или х + 6 = 8 или х + 6 = – 64
х = – 5 или х = 2 или х = – 70
Итак, нашли три возможных значения х. Но, конечно же, среди них могут оказаться посторонние корни. Поэтому нужна проверка – подставим полученные результаты в исходное ур-ние. При х = – 5 получим
Корень подошел. Проверяем следующее число, х = 2:
Корень снова оказался верным. Осталась последняя проверка, для х = – 70:
Итак, все три числа прошли проверку.
Уравнения с «вложенными» радикалами
Порою в ур-нии под знаком радикала стоит ещё один радикал. В качестве примера приведем такую задачу:
При их решении следует сначала избавиться от «внешнего радикала», после чего можно будет заняться и внутренним. То есть в данном случае надо сначала возвести обе части равенства в квадрат:
Внешний радикал исчез. Теперь будем переносить слагаемые, чтобы в одной из частей остался только радикал:
Хочется поделить полученное ур-ние (1) на х, однако важно помнить, что деление на ноль запрещено. То есть, если мы делим на х, то мы должны наложить дополнительное ограничение х ≠ 0. Случай же, когда х всё же равен нулю, мы рассматриваем отдельно. Для этого подставим х = 0 сразу в исходное ур-ние:
Получили верное рав-во, значит, 0 является корнем. Теперь возвращаемся к (1) и делим его на х:
Возводим в квадрат и получаем:
х 2 + 40 = (х + 4) 2
х 2 + 40 = х 2 + 8х + 16
И снова нелишней будет проверка полученного корня:
Иррациональные неравенства
По аналогии с иррациональными ур-ниями иррациональными неравенствами называют такие нер-ва, в которых выражение с переменной находится под знаком радикала или возводится в дробную степень. Приведем примеры иррациональных нер-в:
Нет смысла решать иррациональные нер-ва, если есть проблемы с более простыми, то есть рациональными нер-вами, а также с их системами. Поэтому на всякий случай ещё раз просмотрите этот и ещё вот этот уроки.
Начнем с решения иррациональных неравенств простейшего вида, у которых в одной из частей стоит выражение под корнем, а в другой – постоянное число. Достаточно очевидно, что нер-во вида
Может быть справедливым только тогда, когда
То есть, грубо говоря, нер-ва можно возводить в степень. Однако при этом могут возникнуть посторонние решения. Дело в том, что нужно учитывать и тот факт, что подкоренное выражение должно быть неотрицательным в том случае, если степень корня является четной. Таким образом, нер-во
при четном n можно заменить системой нер-в
Пример. При каких значениях x справедливо нер-во
Решение. С одной стороны, при возведении нер-ва в квадрат мы получим такое нер-во:
х ⩽ – 5 (знак нер-ва изменился из-за того, что мы поделили его на отрицательное число)
Получили промежуток х∈(– ∞; – 5). Казалось бы, надо записать ещё одно нер-во
чтобы подкоренное выражение было неотрицательным. Однако сравните (1) и (2). Ясно, что если (1) выполняется, то справедливым будет и (2), ведь если какое-то выражение больше или равно двум, то оно автоматически будет и больше нуля! Поэтому (2) можно и не решать.
Теперь посмотрим на простейшие нер-ва с корнем нечетной степени.
Пример. Найдите решение нер-ва
Решение. Всё очень просто – надо всего лишь возвести обе части в куб:
x 2 – 7x– 8 2 – 7x– 8 = 0
D = b 2 – 4ac = (– 7) 2 – 4•1•(– 8) = 49 + 32 = 81
Далее полученные точки отмечаются на координатной прямой. Они разобьют ее на несколько промежутков, на каждом из которых функция у =x 2 – 7x– 8 сохраняет свой знак. Определить же этот самый знак можно по направлению ветвей параболы, которую рисует схематично:
Видно, что парабола располагается ниже оси Ох на промежутке (– 1; 8). Поэтому именно этот промежуток и является ответом. Нер-во строгое, поэтому сами числа (– 1) и 8 НЕ входят в ответ, то есть для записи промежутка используются круглые скобки.
Обратите внимание: так как в исходном нер-ве используется корень нечетной (третьей) степени, то нам НЕ надо требовать, чтобы он был неотрицательным. Он может быть меньше нуля.
Теперь рассмотрим более сложный случай, когда в правой части нер-ва стоит не постоянное число, а некоторое выражение с переменной, то есть оно имеет вид
Случаи, когда n является нечетным числом, значительно более простые. В таких ситуациях достаточно возвести нер-во в нужную степень.
Пример. Решите нер-во
Решение.Слева стоит кубический корень, а возведем нер-во в третью степень (при этом мы используем формулу сокращенного умножения):
И снова квадратное нер-во. Найдем нули функции записанной слева, и отметим их на координатной прямой:
D = b 2 – 4ac = (– 1) 2 – 4•1•(– 2) = 1 + 8 = 9
Нер-во выполняется при х∈(– ∞; – 1)⋃(2; + ∞). Так как мы возводили нер-во в нечетную степень, то больше никаких действий выполнять не надо.
стоит корень четной степени, то ситуация резко осложняется. Его недостаточно просто возвести его в n-ую степень. Необходимо выполнение ещё двух условий:
f(x) > 0 (подкоренное выражение не может быть отрицательным);
g(x) > 0 (ведь сам корень должен быть неотрицательным, поэтому если g(x)будет меньше нуля, то решений не будет).
Вообще говоря, в таких случаях аналитическое решение найти возможно, но это тяжело. Поэтому есть смысл решить нер-во графически – такое решение будет более простым и наглядным.
Пример. Решите нер-во
Решение. Сначала решим его аналитически, без построения графиков. Возведя нер-во в квадрат, мы получим
х 2 – 10х + 21 > 0(1)
Решением этого квадратного нер-ва будет промежуток (– ∞;3)⋃(7; + ∞). Но надо учесть ещё два условия. Во-первых, подкоренное выражение должно быть не меньше нуля:
Во-вторых, выражение 4 – х не может быть отрицательным:
Получили ограничение 2,5 ⩽ х ⩽ 4, то есть х∈[2,5; 4]. С учетом того, что при решении нер-ва(1) мы получили х∈(– ∞;3)⋃(7; + ∞), общее решение иррационального нер-ва будет их пересечением, то есть промежутком [2,5; 3):
Скажем честно, что описанное здесь решение достаточно сложное для понимания большинства школьников, поэтому предложим альтернативное решение, основанное на использовании графиков. Построим отдельно графики левой и правой части нер-ва:
Видно, что график корня находится ниже прямой на промежутке [2,5; 3). Возникает вопрос – точно ли мы построили график? На самом деле с его помощью мы лишь определили, что искомый промежуток находится между двумя точками. В первой график корня касается оси Ох, а во второй точке он пересекается с прямой у = 4 – х. Найти координаты этих точек можно точно, если решить ур-ния. Начнем с первой точки:
Итак, координата х первой точки в точности равна 2,5. Для нахождения второй точки составим другое ур-ние:
Это квадратное ур-ние имеет корни 3 и 7 (убедитесь в этом самостоятельно). Число 7 является посторонним корнем:
Подходит только число 3, значит, вторая точка имеет координату х = 3, а искомый промежуток – это [2,5; 3).
Ещё тяжелее случаи, когда в нер-ве с корнем четной степени стоит знак «>», а не « 1/2 = х – 3
Степень с рациональным показателем
Мы уже знакомы с понятием степени с целым показателем. Давайте разберемся, что такое степень с рациональным показателем.
Рациональный показатель – это выражение вида \(\frac
\), где \(p\)-некоторое целое число, а \(q\) – натуральное число, причем \(q\ge2\).
Положительное число \(a\) в рациональной степени \(\frac
\) является арифметическим корнем степени \(q\) из числа \(a\) в степени \(p\):
Обращаем ваше внимание, что
Неважно в каком порядке – сначала извлечь корень или возвести в степень, от этого смысл выражения не теряется. Как удобнее, так и считайте.
Пусть есть некоторое положительное число \(a\) и целое число \(p\), тогда справедливы следующие соотношения:
где \(k\) и \(q\) – натуральные числа большие 1.
Давайте попробуем их доказать:
Из определения степени с рациональным показателем следует, что:
Опять из определения и свойства корня n-й степени следует:
Третья формула на наш взгляд очевидна, просто сократить степень справа и получите исходное выражение.
Свойства степени с рациональным показателем
Пусть \(a\) и \(b\) – некоторые положительные числа, а числа \(m\) и \(n\) – рациональные числа. Тогда выполняются соотношения:
При умножении степеней с рациональным показателем и одинаковым основанием их показатели степени складываются.
При делении степеней с рациональным показателем и одинаковым основанием их показатели степени вычитаются.
При возведении степени с рациональным показателем в степень с рациональным показателем их показатели перемножаются.
Степень с рациональным показателем от произведения двух положительных чисел равна произведению степеней этих множителей.
Степень с рациональным показателем от частного двух положительных чисел равна частному степеней этих чисел.
И еще два очень важных свойства степеней. Они вам понадобятся при решении показательных уравнений и неравенств.
Пусть опять есть некоторое положительное число \(a>1\) и рациональные числа \(n\) и \(m\).
При \(n \gt 0\) \(a^n \gt 1\),
При \(n \lt 0\) \(0 \lt a^n \lt 1\).
Если же \(a \gt 1\) и \(n \gt m\), то
Если \( 0 \lt a \lt 1 \) и \(n \gt m\), то
Разберем несколько примеров:
Так как основание степени больше единицы \(3 \gt 1\) и \(\frac<1> <3>\lt \frac<1><2>\).
Так как \(0 \lt \frac<1> <5>\lt 1\) и \(\frac<1> <3>\lt \frac<1><2>\)
Описание урока
От успешной сдачи государственного экзамена по математике зависит поступление в высшее учебное заведение. Степень с рациональным показателем – важная тема, изучение которой необходимо для успешной подготовки к ЕГЭ. От того, насколько хорошо она освоена, зависит в будущем, насколько легко будет решать уравнения и производить более сложные операции с числами. Задание номер 15 строится на умении работать с такими степенями. Чтобы понимать, о чём идёт речь, стоит ознакомиться с определением степени с рациональным показателем и её основными свойствами, которые пригодятся и при работе с функциями.
Степенью числа А, рациональный показатель которого равен p делённому на q, называют выражение, где под корнем степени q находится возведённое в степень p число A. Чтобы более наглядно рассмотреть это явление, разберём пример. Допустим, число 3 возводится в степень 2/4. Тогда изначальное выражение приобретёт следующий вид: корень четвертой степени от 3 в квадрате. 3 во второй степени — 9. Корень четвертой степени из 9 сложно рассчитать без помощи калькулятора, но существуют примеры, где корень n-ой степени из подкоренного выражения легко извлекается.
Важно запомнить, что число А не должно быть меньше 0, а число q не равно 1.
Свойства степени с рациональным показателем
Знание свойств степеней с показателем, равным рациональному числу, облегчает работу с уравнениями и функциями, где содержатся такие выражения. Внимательно их изучив, можно достаточно быстро выполнять задания, что немаловажно в процессе написания ЕГЭ.
Одно из основных свойств: произведение двух степеней с одинаковым основанием равно основанию в степени, равной сумме степеней двух множителей.
При делении степеней с рациональным показателем из показателя делимого вычитают показатель делителя. У степени с рациональным показателем есть и другие свойства, которые также присущи степени с обыкновенным показателем. Их легко запомнить, а чтобы примеры помогли внимательнее рассмотреть свойства, посмотрите видео, в котором о них рассказывается подробнее.
Преобразование иррациональных выражений в математике с примерами решения и образцами выполнения
Иррациональными выражениями называют выражения, содержащие операцию извлечения корня. Другими словами, иррациональные выражения – это выражения с радикалами (выражения, содержащие в своей записи знаки корня).
Арифметический корень и его свойства
Определение арифметического корня: Пусть а—действительное число, a n — натуральное число, большее единицы. Поставим перед собой задачу: найти число х, такое, чтобы выполнялось равенство
Сначала рассмотрим конкретные примеры.
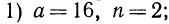
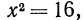
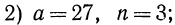
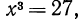
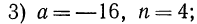
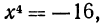
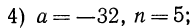
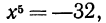
Эти примеры показывают, что поставленная задача при четном 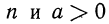
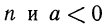
Если задача имеет решение, т. е. равенство 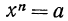
Из рассмотренных выше примеров следует, что существуют два корня второй степени из числа 16 — это числа 4 и -4; существует один корень третьей степени из числа 27 —это число 3; не существует корня четвертой степени из числа —16; существует один корень пятой степени из числа —32—это число —2.
Рассмотрим случай отыскания корня n-й степени из неотрицательного числа. Можно доказать, что если 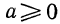
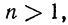
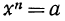
Арифметическим корнем n-й степени из положительного числа а называется такое положительное число, n-я степень которого равна а.
Для арифметического корня n-й степени из числа а принято обозначение 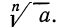
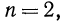
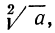
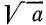
Согласно определению запись 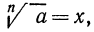
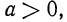

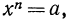
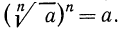
Полагают также
Обратим внимание читателя на то, что, например,
Свойства арифметических корней
Условимся прежде всего о следующем: все переменные, которые встречаются в формулировках свойств и в примерах, рассматриваемых в настоящем и следующем пунктах, будем считать принимающими только неотрицательные значения. Кроме того, мы рассматриваем только арифметические корни, а потому каждый раз специально подчеркивать это не будем. Значит, мы будем писать: «корень n-й степени из неотрицательного числа», а читатель должен понимать, что речь идет об арифметическом корне.
1°. Корень n-й степени из произведения двух неотрицательных чисел равен произведению корней из этих чисел, т. е.
Доказательство:
Мы знаем, что 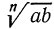
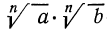
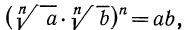
Итак, рассмотрим выражение 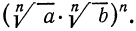
Так как 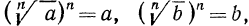
Пример. Вычислить
Решение. По свойству 1° имеем
2°. Корень n-й степени из дроби, числитель которой неотрицателен, а знаменатель положителен, равен корню из числителя, деленному на корень из знаменателя, т. е.
Пример:
Доказательство этого свойства аналогично доказательству свойства 1°.
3°. Чтобы возвести корень n-й степени в натуральную степень k, достаточно возвести в эту степень подкоренное выражение и из полученного результата извлечь корень n-й степени, т. е.
Пример:
Доказательство:
По определению корня 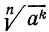
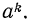
По свойству 3° степени с натуральным показателем (стр. 45) имеем
Так как 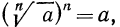
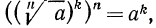
4°. Чтобы извлечь корень из корня, нужно перемножить показатели корней, а подкоренное выражение оставить без изменения, т. е.
Пример:
Доказательство:
значит,
5°. Если показатель корня и показатель степени подкоренного выражения умножить или разделить на одно и то же натуральное число, то значение корня не изменится, т. е.
Пример:
Доказательство:
По определению корня 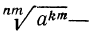
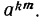
По свойству 3° степени с натуральным показателем имеем
Значит,
Примеры:
Извлечь корень из произведения:
Решение:
а) Применив свойство 1° арифметических корней, получим:
Напомним, что мы в начале рассматриваемого пункта условились считать все переменные принимающими только неотрицательные значения. Не будь этого соглашения, мы не имели бы права писать 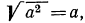
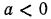
2. Извлечь корень из дроби
Решение:
а) Обратим смешанное число 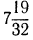
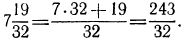
б) воспользовавшись свойствами 2° и 1°, получим
3.Вынести множитель из-под знака корня:
Решение:
а) Представим подкоренное выражение 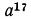
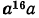
Такое преобразование называется вынесением множителя из-под знака корня. Цель преобразования —упрощение подкоренного выражения;
В некоторых случаях оказывается полезным преобразование, в определенном смысле обратное только что рассмотренному, а именно: внесение множителя под знак корня. Пусть, например, нужно выяснить, какое из чисел больше: 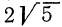
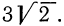
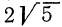
Сделаем аналогичное преобразование числа
Так как
4.Ввести множитель под знак корня:
Решение:
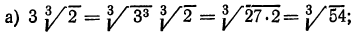
В рассмотренных примерах мы пользовались только определением корня и свойствами 1° и 2°. Рассмотрим теперь примеры использования свойств 3° и 4°.
Решение:
а) По свойству 3° имеем
Обычно стараются подкоренное выражение упростить, для чего выносят множители за знак корня. Имеем:
6.Выполнить действия:
Решение:
а) По свойству 4° арифметических корней имеем
б) преобразуем выражение 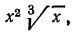
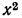
Далее имеем
Рассмотрим, наконец, примеры, в которых используется свойство 5°.
Решение:
а) По свойству 5° мы имеем право показатель корня и показатель степени подкоренного выражения разделить на одно и то же натуральное число. Если в рассматриваемом примере разделить указанные показатели на 3, то получим
8.Упростить выражения:
Решение:
а) Из свойства 1° получаем, что для перемножения корней одной и той же степени достаточно перемножить подкоренные выражения, из полученного результата извлечь корень той же степени; значит,
в) выше мы видели, как перемножить корни одной и той же степени. В данном же примере требуется перемножить корни с различными показателями. Значит, прежде всего мы должны привести радикалы к одному показателю. Согласно свойству 5°, можно показатель корня и показатель степени подкоренного выражения умножить на одно и то же натуральное число; поэтому
А теперь разделим в полученном результате показатели корня и подкоренного выражения на 3:
г) приведем радикалы к одному показателю. Для этого, очевидно, нужно найти наименьшее общее кратное чисел 10 и 15; 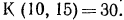
д) НОК чисел 4, 6, 10 равно 60, поэтому приведем все радикалы к показателю 60:
Тождество
Ответим на такой вопрос: если переменная а принимает как неотрицательные, так и отрицательные значения, то чему равен
Если 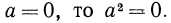
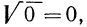

Если 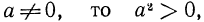
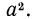
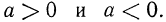
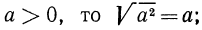
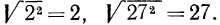
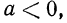
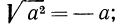
Итак, можно записать, что
Но точно так же определяется модуль действительного числа
Таким образом, 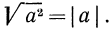
Вообще, если n — четное число, т.е. 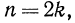
Так, если в рассмотренных примерах 1, а) и б) снять требование неотрицательности значений переменных, то решение примера выглядело бы следующим образом:
Дополнительные замечания о свойствах радикалов
Рассмотренные пять свойств арифметических корней, т. е. пять свойств радикалов безоговорочно верны для неотрицательных подкоренных выражений. Но при решении примеров на действия с радикалами нужно иметь в виду возможность отрицательных значений переменных, содержащихся под знаками радикалов.
Пусть а и b — отрицательные числа, а n — четное число. В этом случае написать 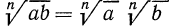
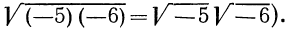
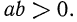
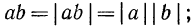
Так как 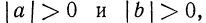
Итак, если n —четное число, а числа а и b имеют одинаковые знаки, то
Очень внимательно следует относиться к свойству 5°. Пусть, например, нужно упростить выражение 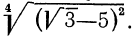
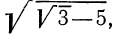
В самом деле, 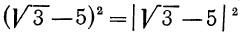
Обобщение понятия о показателе степени
Постановка задачи: Напомним определение степени с натуральным показателем и ее свойства.
Определение
Основные свойства степени
В последующих пунктах речь пойдет об определениях степени с любым рациональным показателем.
Сначала мы определим степень с положительным дробным показателем, далее степень с нулевым показателем и затем степень с отрицательным рациональным показателем. Ясно, что ни на один из этих случаев не переносится данное выше определение, например 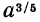
Степень с положительным дробным показателем
Пусть 
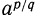
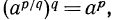
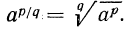
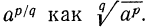
Доказательство. Согласно предложенному определению степени с положительным дробным показателем имеем: 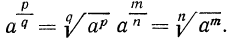
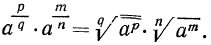
Далее имеем 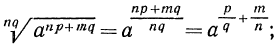
Доказательство:
Воспользуемся свойствами возведения радикала в степень и извлечения корня из корня:
Аналогично можно показать, что будут выполняться свойства:
Итак, при предложенном определении степени с положительным дробным показателем основные свойства степени выполнены. Значит, определение удачно и его можно принять.
Определение:
Если
Например, 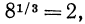
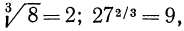
На практике при выполнении действий над радикалами довольно часто переходят к дробным показателям.
Примеры:
Выполнить умножение:
Решение:
2.Разложить на множители
Решение:
Степень с нулевым показателем
При выборе определения мы также будем руководствоваться требованием, чтобы на случай степени с нулевым показателем распространялись свойства 1°—5° степени с натуральным показателем (впрочем, теперь мы уже вправе говорить о распространении свойств степени с положительным рациональным показателем). В частности, при умножении степеней с одинаковым основанием показатели должны складываться, т. е. должно выполняться равенство
так как 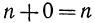
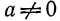

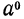
Определение:
Если
Например,
Степень с отрицательным рациональным показателем
Пусть 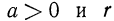
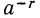
Так как 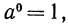
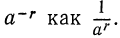
Покажем, например, что
Остальные свойства проверяются аналогично.
Определение:
Если
Например,
Замечание:
Если r—целое число, то полагают а 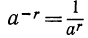
Мы определили понятие степени с любым рациональным показателем. Эта степень обладает следующими свойствами (мы полагаем а > 0, b > 0, 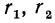
Заметим, что после введения нулевого и отрицательного показателей мы имеем право в свойстве 2° не делать оговорки, что
Тождественные преобразования иррациональных выражении
Тождественно равные выражения на данном множестве: По определению (стр. 47) тождественно равными выражениями называются такие, у которых все соответственные значения равны. Согласно этому определению выражения 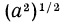
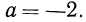
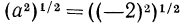
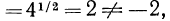
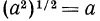
Однако на множестве всех неотрицательных чисел все соответственные значения выражений 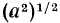
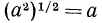
Определение:
Два выражения называются тождественно равными на данном множестве, если на этом множестве они имеют смысл и все их соответственные значения равны.
Например, выражения 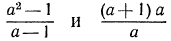
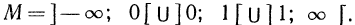
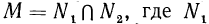
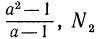
Тождественные преобразования иррациональных выражений
Выражение с переменными называется иррациональным, если оно содержит извлечение корня из переменной или возведение переменной в дробную степень.
Тождественные преобразования иррациональных выражений выполняются, как правило, на множестве неотрицательных чисел. Это вытекает из введенных ранее определений. Например, сократим дробь 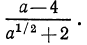
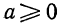
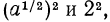
Проделанное нами тождественное преобразование выполнено на множестве неотрицательных чисел, т. е. при 
Примеры:
Решение:
Здесь целесообразно применить прием избавления от иррациональности в знаменателе. Для этого умножим числитель и знаменатель первой дроби на 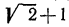
Аналогично поступим со второй дробью (теперь выражением, сопряженным для знаменателя, является
Для того чтобы избавиться от иррациональности в знаменателе третьей дроби, умножим числитель и знаменатель этой дроби на
Таким образом, имеем
Решение:
Прежде всего подумаем, нельзя ли сократить первую дробь. Выражение, стоящее в числителе, можно преобразовать так:
Таким образом, последовательное сокращение дробей при тождественных преобразованиях иррациональных выражений обеспечивает достаточную простоту решения. Проиллюстрируем эту мысль еще на одном примере.
Решение:
Попытка привести дроби, стоящие в числителе, к общему знаменателю без предварительных сокращений этих дробей приведет решение к неоправданному усложнению. Поэтому в первую очередь надо сократить эти дроби, а затем произвести указанные действия:
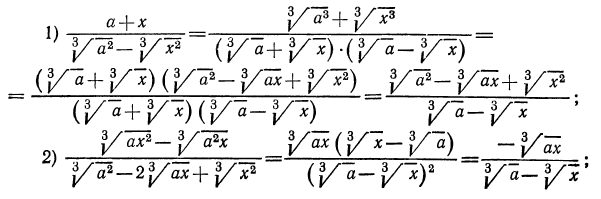
Идея сокращения дробей лежит и в основе тождественных преобразований выражений, содержащих степени с рациональными показателями.
Решение:
Подчеркнем, что проделанные нами в примере 4 тождественные преобразования выполнены на множестве положительных чисел, т. е. при
Иногда множество, на котором выполняются преобразования, имеет более сложную природу. Поясним это на следующем примере.
Решение:
Рассмотрим выражение 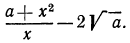
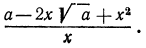
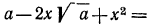
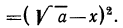
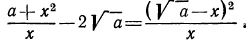
После этих наблюдений мы можем заданное выражение переписать в виде
Выше мы отмечали, что 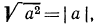
По смыслу примера имеем (заданное выражение содержит 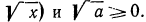
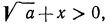
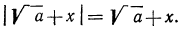
Теперь нужно рассмотреть два случая: 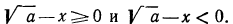
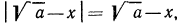
Ответ:
Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:




















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
http://sigma-center.ru/rational_exponent
http://lfirmal.com/preobrazovanie-irracionalnyh-vyrazheniy/