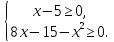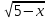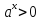Использование графиков функции при решении уравнений

Презентация «Применение графиков при решении уравнений» (9 класс)

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Описание презентации по отдельным слайдам:

Практическое применение графиков функций при решении уравнений и систем уравнений МАОУ СОШ № 13 города ТЮМЕНИ

Графический способ решения уравнения

Графический способ решения систем уравнений

Графическое решение системы уравнений с двумя переменными

Графический способ решения квадратных неравенств

Графическое решение уравнения с параметром

Графическое решение уравнения с параметром

Графическое решение уравнения с параметром

Графическое решение уравнения с параметром

Графическое решение уравнения с параметром

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 924 человека из 80 регионов

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Сейчас обучается 686 человек из 75 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

• Сейчас обучается 309 человек из 69 регионов

Ищем педагогов в команду «Инфоурок»

Дистанционные курсы для педагогов

«Взбодрись! Нейрогимнастика для успешной учёбы и комфортной жизни»

Свидетельство и скидка на обучение каждому участнику

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

5 582 201 материал в базе

Материал подходит для УМК

«Алгебра», Мордкович А.Г., Николаев Н.П.

§ 11. Методы решения систем уравнений

Самые массовые международные дистанционные

Школьные Инфоконкурсы 2022

33 конкурса для учеников 1–11 классов и дошкольников от проекта «Инфоурок»

Другие материалы

• 07.04.2018
• 3031
• 86

• 07.04.2018
• 2441
• 8

• 06.04.2018
• 522
• 1

• 06.04.2018
• 2247
• 4

• 06.04.2018
• 202
• 0

• 05.04.2018
• 1191
• 1

• 04.04.2018
• 937
• 1

• 04.04.2018
• 1913
• 41

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Добавить в избранное

• 07.04.2018 758
• PPTX 2 мбайт
• 22 скачивания
• Рейтинг: 5 из 5
• Оцените материал:

Настоящий материал опубликован пользователем Колчанова Гульнара Рафаильевна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Автор материала

• На сайте: 7 лет и 3 месяца
• Подписчики: 4
• Всего просмотров: 1079276
• Всего материалов: 359

Московский институт профессиональной
переподготовки и повышения
квалификации педагогов

Дистанционные курсы
для педагогов

663 курса от 690 рублей

Выбрать курс со скидкой

Выдаём документы
установленного образца!

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

В России действуют более 3,5 тысячи студенческих отрядов

Время чтения: 2 минуты

Минпросвещения упростит процедуру подачи документов в детский сад

Время чтения: 1 минута

В Ростовской и Воронежской областях организуют обучение эвакуированных из Донбасса детей

Время чтения: 1 минута

Инфоурок стал резидентом Сколково

Время чтения: 2 минуты

В Швеции запретят использовать мобильные телефоны на уроках

Время чтения: 1 минута

В Забайкалье в 2022 году обеспечат интернетом 83 школы

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Методика организации решения уравнений графическим способом как средство формирования графических умений у учащихся

Разделы: Математика

Графический метод обладает рядом преимуществ:

• он часто проще аналитического;
• обладает наглядностью. Особенно когда нет решений или требуется установить количество корней.
• он красив и доставляет эстетическое наслаждение. Выполнять графики нужно в цвете. Это помогает в выборе ответа.

Умение строить графики функций не является самоцелью. Часто построение графиков связано с исследованием поведения функций. Однако необходимость построения графиков облегчают нахождение решений уравнений и неравенств, сокращая или упрощая аналитические выкладки и часто при этом являются единственным методом решения таких задач. Графический метод решения способствует лучшему усвоению ряда понятий: функции, корней уравнения и неравенства, систем уравнений. При этом целесообразно при графическом решении уравнений устанавливать связи с такими свойствами функций как возрастание и убывание, знакопостоянство, обращение функции в ноль и т.д., что помогает глубже понять функциональную зависимость между величинами. Изучение поведения функций и построение их графиков является важным разделом математики. Свободное владение техникой построения графиков часто помогает решать многие задачи и порой является единственным средством их решения. Кроме того, умение строить график представляет большой самостоятельный интерес. Материал, связанный с построением графиков функций, в средней школе изучается недостаточно полно с точки зрения требований, предъявляемых на экзаменах. Поэтому задачи на построение графиков нередко вызывают затруднения у учащихся.

Для того, чтобы по графикам можно было получать достаточно приемлемые числовые ответы, графики должны быть особенно тщательно построены. Решается задача организации работы таким образом, чтобы выработать навыки быстрого построения графиков элементарных функций и их преобразований. Работа над формированием графических умений начинается с 5-го класса.

Изящно выполненная работа способствует развитию чувства красоты, удовлетворения от проделанной работы.

Изучение поведения функций и построение их графиков являются важным разделом школьного курса. Свободное владение техникой построения графиков часто помогает решать сложные задачи, а порой является единственным средством их решения. Кроме того, умение строить графики функций представляет большой интерес для самих учащихся. Однако на базе основной школы материал, связанный с этим вопросом, представлен несколько хаотично, изучается недостаточно полно, многие важные моменты не входят в программу.

Цель – прояснить и дополнить школьный материал, связанный с функциями и построение их графиков, применением их к решению уравнений, их систем.

В требованиях к уровню подготовки выпускников по разделу «Функции и графики» прописано:

• решать уравнения, системы уравнений, используя свойства функций и их графические представления;
• находить приближённые решения уравнений и их систем, используя графический метод.

В преподавание алгебры по учебнику под редакцией А.С.Теляковского. Линейная функция и функции у=х 2 , у=х 3 изучаются в 7 классе. Практически не вырабатываются навыки в применении графиков этих функций. Единственное упражнение: найти координаты точек пересечения графиков функций у=8,5х и у=0,5х-19,5. графики линейных функций только иллюстрируют решение систем линейных уравнений.

Автор вводит некоторые упражнения, необходимые в дальнейшем при решении уравнений и их систем:

— постройте в одной и той же координатной плоскости а) у=х 2 ; у=4; б) у=х 2 ; у=2х.

— изобразите схематически графики функций у = -0,9х + 4; у = 2,3х; у = х/10 . Но упражнения вводятся как дополнительные. И в «Задачах повышенной трудности» (в конце учебника) есть уравнения, которые тоже можно решать графическим способом: |х -3| = 7; |х+2| = 9; |4 — х| = 1,5.

В 8 классе изучаются функции у = к/х; у =. Представлены функции у = 4/|х|, у = -6/|х|.

— Могут ли графики функций у=к/х и у = ах +в пересекаться

а) в одной точке;

б) в двух точках;

в) в трёх точках.

— Могут ли графики функций у = к/х и у = ах +в пересекаться в двух точках, лежащих

а) в одной четверти;

б) в первой и второй четвертях;

в) в первой и третьей четвертях.

Опять же эти упражнения в дополнительных.

В 8 классе обучающихся знакомят с графическим способом решения уравнений (8/х = -х+6; (8/х = х 2 ). Появляются уравнения третьей степени, которые не решаются аналитическим способом. (х 3 — х + 1 = 0; х 3 + 2х — 4=0) На изучение этой темы отводится 1 час.

В 9 классе подробно изучается квадратичная функция и её график. Получены обучающимися представления о преобразовании графического объекта относительно осей координат. Именно в это время отрабатываются навыки в построении параболы. Но данные преобразования почти не переносятся на преобразования других графических объектов. Хотя есть два упражнения, которые соотносятся с заданиями, встречающимися в материалах ЕГЭ.

На рисунке изображён график одной их функций . Какой именно?

— Какой из трёх графиков, изображённых на рисунке, является графиком функции у = |х -2|

Сделаны попытки преобразования графических объектов.

— Какие преобразования надо выполнить, чтобы

а) из графика функции у=х 3 получить графики функций у = — х 3 ; у = (х-3) 3 ; у = х 3 + 4.

б) из графика функции у = получить графики функций у = — ;

— Постройте в одной координатной плоскости графики функций у = | х|; у =|х -4| ; у = |х -4|-3.

В учебнике 9 класса в главе «Целое уравнение и его корни» упоминается графический способ уравнений третьей и более высокой степени как один из способов наряду с разложением на множители.

Поэтому: уже в 7 классе строим графики функций у = | х| — 3, у = 4 — | х|; у =|х +4|; у = | х — 3|.

При построении параболы вводим первые преобразования:

— построить графики функций у = х 2 +3; у=х 2 -5, где смещение по оси ординат. А затем у = (х+2) 2 ; у = (х-1) 2 . Конечно, не все ученики усваивают, впрочем, как и всё содержание материала. Для успешных учеников это не сложно. Тем более это только пропедевтика.

В 8-м классе: Урок-практикум.

Тема: «График функции у = . Графический способ решения иррациональных уравнений»

Цель: отработать навыки в преобразовании графика функции у = , закрепить умения графически решать иррациональные уравнения.

I. Фронтально

1). Схематически в одной системе координат изобразить графики функций

2). Решить уравнения

II. Построить графики функций

III. Решение уравнений

X 2 -3 =

В 8 классе строим преобразования гиперболы и графика функции у = .

Упражнения взяты из «Сборника задач по алгебре 8-9 класса» М.Л.Галицкого, А.И.Звавича. Уже на факультативных занятиях или занятиях кружка решаем уравнения с параметром |х 2 -2х-3| = а. Определить, при каком а уравнение имеет три корня. Строим графики функций у = |х 2 -2х-3|; у = а. Получаем ответ а = 4.

В 9 классе больше занимаемся исследованием квадратного трёхчлена. Формулы функций усложняю. Рассматриваем графики вида у = (х 2 -2) 2 — (х 2 -1) 2 ;

Необычность конструкций, разрыв графиков, удаление точек вызывает некоторую удивлённость. Тем самым преодолевается стандартность мышления, развивается воображение, повышается интерес: а что ещё может получиться? В каких случаях?

Уравнения, решаемые графическим способом.

I. Решение уравнений Р(х) = 0, где Р(х) – многочлен степени большей 2.

Применение свойств функций для решения уравнений

В работе рассматриваются сособы решения уравнений с использованием свойств и характеристик функций: монотонности, ограниченности, области определенийи области значений функции.

Просмотр содержимого документа
«Применение свойств функций для решения уравнений»

II. Применение свойств функций для решения уравнений

Использование ОДЗ для решения уравнений .………….. 2стр

Монотонность функции и наличие корней уравнении…. 3стр

Используемая литература………………………………………. 10 стр

Найти и освоить приемы решения уравнений способами, позволяющими значительно сократить время нахождения корней уравнений.

В ходе сбора и изучения информации по данной теме, были найдены и изучены рациональные приемы решения уравнений с применением свойств монотонности, ограниченности функций, а также области определения и значений функций, позволяющие эффективно (практически устно) решать некоторые виды уравнений, рассмотренных в качестве примеров в нашей работе.

В наших школьных учебниках алгебры в основном изучаются такие методы и приемы решения уравнений как возведение в степень, замена переменной, применение тождественных преобразований, Но использование этих способов при решении некоторых видов уравнений приводит к довольно долгим и сложным преобразованиям, особенно если уравнения в левой и правой части которой находятся функции, имеющие различную природу.

В ходе наших поисков мы познакомились с одним из эффективных способов решения уравнений вида f(x)=g(x), который и демонстрируем в нашей работе. Это способ решения уравнений с использованием свойств функций.

Начнем с уравнений, которые можно решить, используя область определения функции или область допустимых значений переменной. Напомним, что множество значений переменной, при которых обе части данного уравнения (или неравенства) имеют смысл называют областью допустимых значений уравнения или неравенства. Рассмотрим такие уравнения, которые можно решить просто найдя ОДЗ.

​​​ = 3−x

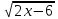
Пусть f(x) = 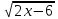. Тогда D (f) определяется неравенством 2х – 6≥ 0, т.е. x≥3, а E(f) = [0; +∞ )

Значит правая часть уравнения должна быть неотрицательной, т.е. должно выполнятся условие 3−x ≥ 0, тогда x ≤ 3. Определяется системой двух неравенств: x≥3 и x ≤ 3. Получаем, что ОДЗ уравнения: х=3.Легко видеть, что 3 будет корнем исходного уравнения.

Приведем еще один пример уравнения:

​​+​ ​​​= 27x−15

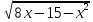
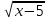
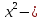
Решение: Найдем ОДЗ, решив систему неравенств

Решая неравенства этой системы получим 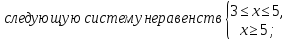А эта система имеет решение х=5. Таким образом, уравнение имеет смысл только при одном значении переменной. Подставив x=5 в уравнение, убеждаемся, что получаем верное равенство. Значит 5 – корень данного уравнения.

Монотонность функции и наличие корней уравнения.

Рассмотрим как применяются такое свойство функции как монотонность. Для успешного решения уравнения этим способом необходимо знать следующие утверждения: 1) если функция f (х) на некотором промежутке возрастает, а функция g(х) убывает на этом же промежутке, то уравнение f(х) = g(х) имеет на этом промежутке не более одного корня; 2) Если на некотором промежутке функция f(x) возрастает (или убывает), то уравнение f(x)=a на этом промежутке имеет единственный корень либо не имеет корней (a — постоянная величина (число)). Применение свойства продемонстрируем на следующих примерах:

1) x 1991 +1 =

1) В левой части этого уравнения стоит возрастающая функция на на R
в правой – убывающая на (-∞;5].
Если уравнение и будет иметь корень, то только на промежутке (-∞;5]. Легко заметить, что этот корень 1, и он, согласно теореме, единственный.

2) 5x 19 + 4x 3 +3х=12. Функция, стоящая в левой части уравнения является возрастающей (как сумма возрастающих функций). Следовательно, уравнение имеет не более одного корня. Подбором находим, что x=1.

3) +=2. Областью определения функции, стоящей в левой части, является промежуток [-1; ∞). На этом промежутке функция возрастает. Следовательно, корень, равный -1 – единственный.

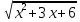
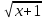
4) 2 x 15 + 3x=5/х. Функция f(x) = 5/х на каждом из промежутков (-∞;0) и (0:∞) убывает, а функция g (х) = 2 x 15 + 3x возрастает на каждом из них, поэтому наше уравнение на каждом из этих промежутков имеет не более одного корня. Убеждаемся, что это числа 1 и -1.

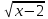
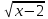
5) 2= 9/х – 1.Функция f(x)= 2 на промежутке [ 2; ∞) возрастает, а функция g (х) = 9/х – 1 на этом же промежутке убывает, значит уравнение имеет не более одного корня на этом промежутке. И этот корень равен 3.

6) найти положительные корни уравнения

Функция 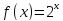возрастает на R. g (х)=
Убывает на промежутке [ 0; ∞). Следовательно, на промежутке [ 0; ∞) уравнение имеет не более одного корня. Подбором находим что х =1.

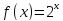
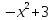
Функция возрастает на(0; ∞) . а функция g (х)= на этом промежутке убывает. Значит, уравнение будет иметь корни только на промежутке (0; ∞). Подбором находим корень уравнения –это число 2.

Рассмотрим, как можно применить к решению уравнений такое свойство функции как ограниченность. Метод, с помощью которого решаются уравнения с применением ограниченности функции, получил название метода мажорант. Ну, а само название метода происходит от французского слова majorer — объявлять большим. Мажорантой данной функции f(х) на множестве Р, называется такое число М, что либо f(х) ≤ М для всех х ϵ Р, либо f(х) ≥ М для всех х ϵ Р. Основная идея метода состоит в следующем: Пусть имеется уравнение f(х) = g(х) и существует такое такое число М, что для любого х из области определения f(х) и g(х) имеем f(х) ≤ М и g(х) ≥ М. Тогда уравнение f(х) = g(х) равносильно системе 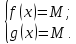Метод применим к уравнениям, в которых используются ограниченные фукции, т. е. функции, множество значений которых ограниченно. Вот некоторые из них:

1. -1≤sinx≤1 или ≤1

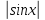
2. -1≤cosx≤1 или 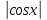≤1

3.

4.

5.

6.

Применение метода рассмотрим на следующих примерах.

1) Решим уравнение: + =0.

4и 10 степени – это четные числа, значит и при любом значении x. Тогда наше уравнение будет равносильно системе уравненийПервое уравнение имеет единственный корень – это число3, значит, если система и будет иметь решение, то не более одного. Проверкой убеждаемся, что3 является корнем и второго уравнения системы, а следовательно и исходного уравнения.

Заменим левую часть уравнения логарифмом, используя свойство разности логарифмов:

Представим дробь в виде , и используя неравенство Коши оценим подлогарифмическое выражение. Получаем (x + ) ≥ 4, а значит

log₂ (x + ) ≥ 2. Таким образом, левая часть уравнения не меньше 2.

Рассмотрим правую часть уравнения. В правой части содержится квадратный трехчлен, поэтому выделив из него квадрат двучлена приходим к выводу, что данное выражение принимает значения не больше 2:

4 x – x 2 – 2 = – x 2 + 4 x – 2 = – ( – 4 x + 4 – 2) = – (x — 2) 2 + 2 = 2 – ( x — 2) 2

Получили, что правая часть уравнения не больше 2, т.к. (x — 2) 2 ≥ 0 при любых х. Значит, равенство левой и правой частей уравнения достигается, если они одновременно равны 2.

Из первого уравнения системы находим корень х = 2. Убеждаемся, что этот корень удовлетворяет и второму уравнению системы. Следовательно, решением исходного уравнения будет х = 2.

3) Решить уравнение:

В левой части уравнения стоит тригонометрическая функция, а в правой – сумма показательных. Формул, позволяющих находить корни в таких случаях, не существует. Оценим каждую из частей уравнения. Очевидно, что левая часть уравнения не больше 2. И так как

Поскольку 0, то причем равенство достигается только при x = 0. В данном случае

Получили, что левая часть уравнения не больше двух, а правая часть – больше или равняется двум. Таким образом, уравнение имеет решение, только если имеет решение система уравнений:

Проверкой убеждаемся, что x=0 – корень уравнения: . Значит число 0 – корень исходного уравнения. Получили ответ: x = 0.

Рассмотрим решение еще одного уравнения:

Рассмотрим две функции

Уравнение имеет решение, если наибольшее значение функции f(х) равно наименьшему значению функции g(х). Таким образом, уравнение имеет решение, только если обе части равны 2. И наше уравнение равносильно системе:

Решим первое уравнение системы:

Подставив данный корень во второе уравнение системы, получим верное равенство. Значит, решением исходного уравнения будут числа вида .

Функция y= (квадратичная функция) имеет наименьшее значение при , равное y(2)=4

Функция у= является возрастающей и, следовательно, принимает наименьшее значение при x=2

Правая часть уравнения, в силу ограниченности функции принимает значения не больше 2, поэтому исходное уравнение равносильно системе:

Так как 2-корень первого уравнения, то убедимся, что число 2-корень второго уравнения. Получаем:

Таким образом, 2-корень исходного уравнения.

Рассмотренные нами примеры могли быть решены и другими методами, но традиционные методы в данных конкретных примерах достаточно трудоемки. В нашей работе мы постарались продемонстрировать применение некоторых нестандартных приемов решения уравнений, основанных на свойствах и характеристиках функций. Планируем продолжить изучение нетрадиционных и эффективных приемов решения уравнений.