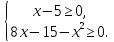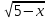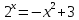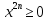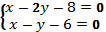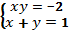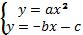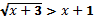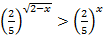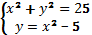Использование свойств и графиков функций для решения уравнений

Технологическая карта 11 класс «Использование свойств функций при решении уравнений и неравенств»

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Технологическая карта урока математики

Учитель математики Дмитриева Г.Ш.

МБОУ «Средняя общеобразовательная школа с углубленным изучением отдельных предметов №55 имени Александра Невского» г. Курска

Алгебра и начала математического анализа

11 класс. Учебник для 11 класса, Никольский С.М.

Использование свойств функций при решении уравнений и неравенств

Урок обобщения и систематизации полученных знаний

Формирование навыков решения уравнений и неравенств с помощью свойств функций.

Повторение метода промежутков для уравнений.

Развитие вычислительных навыков учащихся, формирование умения проводить анализ, обобщать, делать выводы.

Воспитание умения вести диалог, самостоятельности мышления, интереса к предмету.

Авторская мультимедийная презентация, экран, кейсы для работы в парах, доска

Формы организации деятельности обучающихся

Индивидуальная работа; работа в парах; фронтальная работа

Формирование навыков решения уравнений и неравенств с помощью использования свойств функций. Умение применять математические знания при выполнении практических заданий.

Умение выдвигать гипотезу, отстаивать или опровергать ее. Умение находить в источниках необходимую информацию для решения математических проблем.

Умение записывать ход решения по образцу. Умение грамотно излагать свои мысли, дополнять и исправлять ответы других учащихся, находить другие способы решения.

Устное сообщение учителя

Учитель приветствует класс, создает позитивный настрой на урок

Приветствуют учителя, настраивают-ся на работу, концентриру-ют внимание, получают позитивный заряд

Регулятивные: способность регулировать свои действия, прогнозиро-вать деятель-ность на уроке

Метод промежут-ков для уравнений и нера-венств

Решение уравнений и неравенств

1. Метод промежутков при решении уравнений с модулем

Устно повторить алгоритм решения уравнения с модулем методом промежутков

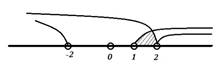
На промежутке (-∞;2)

x = -4 — принадлежит промежутку (-∞; 2)

На промежутке [2;3)

x =4 — не принадлежит промежутку [2;3)

На промежутке [3;+∞)

x =6 – принадлежит промежутку [3;+∞)

Таким образом, исходное уравнение имеет два корня:

2. Метод интервалов для непрерывных функций

D ( f ) – область существования функции f ( x ) – множество решений системы неравенств

Проверка показывает, что числа -2 и 2 являются решениями исходного неравенства.

Нули функции f ( x ) числа 6 и 9 и они не являются решениями исходного неравенства.

Определим знак функции f ( x ) на каждом из четырех интервалов:

Выберем множество всех решений неравенства. Это объединение интервалов (-∞; -2), (2;6), (9;10) и точки -2 и 2.

Ответ: (-∞; -2] U [2;6) U (9;10).

Устно повторяют алгоритм решения уравнения с модулем методом промежутков, применяют его на практике

Регулятивные: способность провести самооценку

Актуализа-ция знаний, умение проводить анализ, обобщать, делать выводы

Использо-вание областей существо-вания функций

Решение уравнений и неравенств

1. Устно вспомнить свойства функций (область определения, неотрицательности, ограничен-ности, монотонности и т.д.), свойства синуса и косинуса.

2. Использование свойств функ-ций при решении уравнений и неравенств

3. Применение теории на практи-ке.

Решим уравнение (учебник п.13.1 пример 1, с.314-315):

Обе части уравнения определены лишь для таких x , которые удовлетворяют системе неравенств:

Этой системе удовлетворяют лишь два числа x =4 и x = -4. Проверка показывает, что число 4 удовлетворяет исходному неравенству, а число -4 – не удовлетворяет неравенству. Следовательно, неравенство имеет единственное решение x=4 .

Устно повторяют свойства функций и свойства синуса и косинуса, применяют знания на практике.

Личностные: осознание своих возмож-ностей; анализируя и вспоминания теорию, нахо-дят необходи-мую информа-цию для реше-ния уравнений и неравенств.

Регулятивные: целеполагание, прогнозирова-ние

Использование неот-рицатель-ности фун-кций, ис-

пользова-ние огра-ниченнос-ти функ-ций

Самостоятельно, работа в парах на местах, два человека за доской

№ 13.2 (а) – решить уравнение

№ 13.4 (а) – решить неравенство

Использование неотрицательности функций

Каждая функция неотрицательна для любого x из области существования и их сумма равна нулю тогда и только тогда, когда каждая из них равна нулю.

x =7 – единственное решение.

Использование ограниченности функций

f ( x ) – квадратичная функция, гра-фик парабола, ветви направлены вверх, вершина (2;1).

– тригонометрическая функция, график синусоида,

Решим любое из них

Проверка показала, что x =2 единственное решение.

Устное сообщение учителя, учащихся

Выводы, проставление отметок

Отвечают на вопросы, получают оценки по результатам выполненной работы

Личностные: умение провес-ти самооценку и организовать взаимооценку.

Регулятивные: построение ло-гической це-почки рассуж-дений и дока-зательство.

Информа-ция о до-машнем задании

Учитель информирует о домашнем задании:

§13, №13.2(б), 13.4(б), 13.8(б), 13.14(б).

Записывают домашнее задание.

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 925 человек из 80 регионов

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Сейчас обучается 684 человека из 75 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

• Сейчас обучается 309 человек из 69 регионов

Ищем педагогов в команду «Инфоурок»

Дистанционные курсы для педагогов

«Взбодрись! Нейрогимнастика для успешной учёбы и комфортной жизни»

Свидетельство и скидка на обучение каждому участнику

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

5 579 007 материалов в базе

Материал подходит для УМК

«Математика: алгебра и начала математического анализа, геометрия. Алгебра и начала математического анализа (базовый и углублённый уровни)», Никольский С.М., Потапов М.К., Решетников Н.Н. и др.

Самые массовые международные дистанционные

Школьные Инфоконкурсы 2022

33 конкурса для учеников 1–11 классов и дошкольников от проекта «Инфоурок»

Другие материалы

• 01.04.2018
• 607
• 18

• 01.04.2018
• 20872
• 5

• 01.04.2018
• 1540
• 3

• 01.04.2018
• 3030
• 25

• 01.04.2018
• 1062
• 2

• 01.04.2018
• 287
• 2

• 01.04.2018
• 418
• 6

• 01.04.2018
• 283
• 0

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Добавить в избранное

• 01.04.2018 2165
• DOCX 64 кбайт
• 100 скачиваний
• Оцените материал:

Настоящий материал опубликован пользователем Дмитриева Галия Шамильевна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Автор материала

• На сайте: 3 года и 10 месяцев
• Подписчики: 0
• Всего просмотров: 3558
• Всего материалов: 5

Московский институт профессиональной
переподготовки и повышения
квалификации педагогов

Дистанционные курсы
для педагогов

663 курса от 690 рублей

Выбрать курс со скидкой

Выдаём документы
установленного образца!

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

В школах Хабаровского края введут уроки спортивной борьбы

Время чтения: 1 минута

В Забайкалье в 2022 году обеспечат интернетом 83 школы

Время чтения: 1 минута

Приемная кампания в вузах начнется 20 июня

Время чтения: 1 минута

Тринадцатилетняя школьница из Индии разработала приложение против буллинга

Время чтения: 1 минута

Полный перевод школ на дистанционное обучение не планируется

Время чтения: 1 минута

В Курганской области дистанционный режим для школьников продлили до конца февраля

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Применение свойств функций для решения уравнений

В работе рассматриваются сособы решения уравнений с использованием свойств и характеристик функций: монотонности, ограниченности, области определенийи области значений функции.

Просмотр содержимого документа
«Применение свойств функций для решения уравнений»

II. Применение свойств функций для решения уравнений

Использование ОДЗ для решения уравнений .………….. 2стр

Монотонность функции и наличие корней уравнении…. 3стр

Используемая литература………………………………………. 10 стр

Найти и освоить приемы решения уравнений способами, позволяющими значительно сократить время нахождения корней уравнений.

В ходе сбора и изучения информации по данной теме, были найдены и изучены рациональные приемы решения уравнений с применением свойств монотонности, ограниченности функций, а также области определения и значений функций, позволяющие эффективно (практически устно) решать некоторые виды уравнений, рассмотренных в качестве примеров в нашей работе.

В наших школьных учебниках алгебры в основном изучаются такие методы и приемы решения уравнений как возведение в степень, замена переменной, применение тождественных преобразований, Но использование этих способов при решении некоторых видов уравнений приводит к довольно долгим и сложным преобразованиям, особенно если уравнения в левой и правой части которой находятся функции, имеющие различную природу.

В ходе наших поисков мы познакомились с одним из эффективных способов решения уравнений вида f(x)=g(x), который и демонстрируем в нашей работе. Это способ решения уравнений с использованием свойств функций.

Начнем с уравнений, которые можно решить, используя область определения функции или область допустимых значений переменной. Напомним, что множество значений переменной, при которых обе части данного уравнения (или неравенства) имеют смысл называют областью допустимых значений уравнения или неравенства. Рассмотрим такие уравнения, которые можно решить просто найдя ОДЗ.

​​​ = 3−x

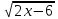
Пусть f(x) = 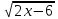. Тогда D (f) определяется неравенством 2х – 6≥ 0, т.е. x≥3, а E(f) = [0; +∞ )

Значит правая часть уравнения должна быть неотрицательной, т.е. должно выполнятся условие 3−x ≥ 0, тогда x ≤ 3. Определяется системой двух неравенств: x≥3 и x ≤ 3. Получаем, что ОДЗ уравнения: х=3.Легко видеть, что 3 будет корнем исходного уравнения.

Приведем еще один пример уравнения:

​​+​ ​​​= 27x−15

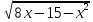
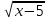
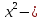
Решение: Найдем ОДЗ, решив систему неравенств

Решая неравенства этой системы получим 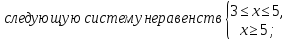А эта система имеет решение х=5. Таким образом, уравнение имеет смысл только при одном значении переменной. Подставив x=5 в уравнение, убеждаемся, что получаем верное равенство. Значит 5 – корень данного уравнения.

Монотонность функции и наличие корней уравнения.

Рассмотрим как применяются такое свойство функции как монотонность. Для успешного решения уравнения этим способом необходимо знать следующие утверждения: 1) если функция f (х) на некотором промежутке возрастает, а функция g(х) убывает на этом же промежутке, то уравнение f(х) = g(х) имеет на этом промежутке не более одного корня; 2) Если на некотором промежутке функция f(x) возрастает (или убывает), то уравнение f(x)=a на этом промежутке имеет единственный корень либо не имеет корней (a — постоянная величина (число)). Применение свойства продемонстрируем на следующих примерах:

1) x 1991 +1 =

1) В левой части этого уравнения стоит возрастающая функция на на R
в правой – убывающая на (-∞;5].
Если уравнение и будет иметь корень, то только на промежутке (-∞;5]. Легко заметить, что этот корень 1, и он, согласно теореме, единственный.

2) 5x 19 + 4x 3 +3х=12. Функция, стоящая в левой части уравнения является возрастающей (как сумма возрастающих функций). Следовательно, уравнение имеет не более одного корня. Подбором находим, что x=1.

3) +=2. Областью определения функции, стоящей в левой части, является промежуток [-1; ∞). На этом промежутке функция возрастает. Следовательно, корень, равный -1 – единственный.

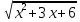
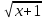
4) 2 x 15 + 3x=5/х. Функция f(x) = 5/х на каждом из промежутков (-∞;0) и (0:∞) убывает, а функция g (х) = 2 x 15 + 3x возрастает на каждом из них, поэтому наше уравнение на каждом из этих промежутков имеет не более одного корня. Убеждаемся, что это числа 1 и -1.

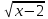
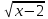
5) 2= 9/х – 1.Функция f(x)= 2 на промежутке [ 2; ∞) возрастает, а функция g (х) = 9/х – 1 на этом же промежутке убывает, значит уравнение имеет не более одного корня на этом промежутке. И этот корень равен 3.

6) найти положительные корни уравнения

Функция 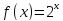возрастает на R. g (х)=
Убывает на промежутке [ 0; ∞). Следовательно, на промежутке [ 0; ∞) уравнение имеет не более одного корня. Подбором находим что х =1.

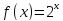
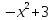
Функция возрастает на(0; ∞) . а функция g (х)= на этом промежутке убывает. Значит, уравнение будет иметь корни только на промежутке (0; ∞). Подбором находим корень уравнения –это число 2.

Рассмотрим, как можно применить к решению уравнений такое свойство функции как ограниченность. Метод, с помощью которого решаются уравнения с применением ограниченности функции, получил название метода мажорант. Ну, а само название метода происходит от французского слова majorer — объявлять большим. Мажорантой данной функции f(х) на множестве Р, называется такое число М, что либо f(х) ≤ М для всех х ϵ Р, либо f(х) ≥ М для всех х ϵ Р. Основная идея метода состоит в следующем: Пусть имеется уравнение f(х) = g(х) и существует такое такое число М, что для любого х из области определения f(х) и g(х) имеем f(х) ≤ М и g(х) ≥ М. Тогда уравнение f(х) = g(х) равносильно системе 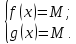Метод применим к уравнениям, в которых используются ограниченные фукции, т. е. функции, множество значений которых ограниченно. Вот некоторые из них:

1. -1≤sinx≤1 или ≤1

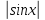
2. -1≤cosx≤1 или 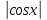≤1

3.

4.

5.

6.

Применение метода рассмотрим на следующих примерах.

1) Решим уравнение: + =0.

4и 10 степени – это четные числа, значит и при любом значении x. Тогда наше уравнение будет равносильно системе уравненийПервое уравнение имеет единственный корень – это число3, значит, если система и будет иметь решение, то не более одного. Проверкой убеждаемся, что3 является корнем и второго уравнения системы, а следовательно и исходного уравнения.

Заменим левую часть уравнения логарифмом, используя свойство разности логарифмов:

Представим дробь в виде , и используя неравенство Коши оценим подлогарифмическое выражение. Получаем (x + ) ≥ 4, а значит

log₂ (x + ) ≥ 2. Таким образом, левая часть уравнения не меньше 2.

Рассмотрим правую часть уравнения. В правой части содержится квадратный трехчлен, поэтому выделив из него квадрат двучлена приходим к выводу, что данное выражение принимает значения не больше 2:

4 x – x 2 – 2 = – x 2 + 4 x – 2 = – ( – 4 x + 4 – 2) = – (x — 2) 2 + 2 = 2 – ( x — 2) 2

Получили, что правая часть уравнения не больше 2, т.к. (x — 2) 2 ≥ 0 при любых х. Значит, равенство левой и правой частей уравнения достигается, если они одновременно равны 2.

Из первого уравнения системы находим корень х = 2. Убеждаемся, что этот корень удовлетворяет и второму уравнению системы. Следовательно, решением исходного уравнения будет х = 2.

3) Решить уравнение:

В левой части уравнения стоит тригонометрическая функция, а в правой – сумма показательных. Формул, позволяющих находить корни в таких случаях, не существует. Оценим каждую из частей уравнения. Очевидно, что левая часть уравнения не больше 2. И так как

Поскольку 0, то причем равенство достигается только при x = 0. В данном случае

Получили, что левая часть уравнения не больше двух, а правая часть – больше или равняется двум. Таким образом, уравнение имеет решение, только если имеет решение система уравнений:

Проверкой убеждаемся, что x=0 – корень уравнения: . Значит число 0 – корень исходного уравнения. Получили ответ: x = 0.

Рассмотрим решение еще одного уравнения:

Рассмотрим две функции

Уравнение имеет решение, если наибольшее значение функции f(х) равно наименьшему значению функции g(х). Таким образом, уравнение имеет решение, только если обе части равны 2. И наше уравнение равносильно системе:

Решим первое уравнение системы:

Подставив данный корень во второе уравнение системы, получим верное равенство. Значит, решением исходного уравнения будут числа вида .

Функция y= (квадратичная функция) имеет наименьшее значение при , равное y(2)=4

Функция у= является возрастающей и, следовательно, принимает наименьшее значение при x=2

Правая часть уравнения, в силу ограниченности функции принимает значения не больше 2, поэтому исходное уравнение равносильно системе:

Так как 2-корень первого уравнения, то убедимся, что число 2-корень второго уравнения. Получаем:

Таким образом, 2-корень исходного уравнения.

Рассмотренные нами примеры могли быть решены и другими методами, но традиционные методы в данных конкретных примерах достаточно трудоемки. В нашей работе мы постарались продемонстрировать применение некоторых нестандартных приемов решения уравнений, основанных на свойствах и характеристиках функций. Планируем продолжить изучение нетрадиционных и эффективных приемов решения уравнений.

МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ ПРАКТИЧЕСКОЙ РАБОТЫ ПО МАТЕМАТИКЕ — Тема: Использование свойств и графиков функций для решения уравнений и неравенств

МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ ПРАКТИЧЕСКОЙ РАБОТЫ ПО МАТЕМАТИКЕ В СПО

Разработал преподаватель: Игнатьева Елена Сергеевна

Использование свойств и графиков функций для решения уравнений и неравенств

— применить умения по владению стандартными приемами решения уравнений и систем.

1. Рабочая тетрадь в клетку

2. Раздаточные материалы: карточки-задания, инструкционные карты – 20 штук.

3. Калькулятор простой.

1. Решите неравенство графически

2. Решите графически систему уравнений.

3. Решить графически уравнение.

1. Внимательно прочитать тему и цель практической работы .

2. Изучить учебный материал по теме.

3. Ответить на вопросы.

4. Выполнить задания.

5. Подготовить отчет.

Пояснения к работе (учебный материал):

Если графики функций пересекаются в одной точке, то уравнение имеет один корень, если в двух, то два решения.

Если графики не пересекаются, то уравнение не имеет корней.

Первый способ графического решения квадратного уравнения заключается в построении параболы y = ax 2 + bx + c и нахождении корней уравнения ax 2 + bx + c =0 как абсцисс точек пересечения параболы с осью О x .

Если парабола пересекает ось О x в двух точках, то соответствующее уравнение имеет два действительных корня;

если парабола касается оси О x , то уравнение имеет два равных действительных корня;

наконец, если парабола не пересекает Ось О x , то уравнение не имеет действительных корней.

Второй способ графического решения квадратного уравнения заключается в том, что уравнение в виде

При выполнении практической работы рассмотрите следующие примеры:

Выяснить с помощью графиков, сколько корней имеет уравнение / Найти приближённое значение этих корней.

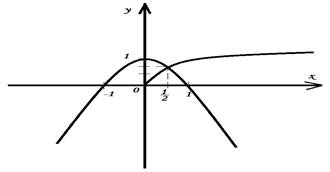
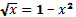
Решение: Построим на одном рисунке 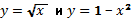, используя свойства этих функций.

Графики пересекаются в одной точке (≈0,5; ≈0,75)

Решите неравенство

Решение. Неравенство удобно решить графически.

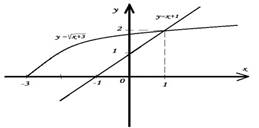
Построим на одном чертеже графики функций 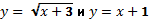, используя свойства функций.

Ответ: -3 ≤ x

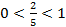
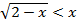
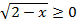
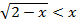
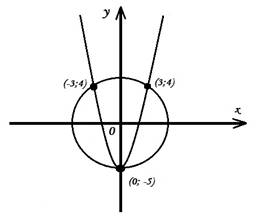
Решение. Неравенство показательное, т.к. , то данное неравенство равносильно неравенству , область определения которого − промежуток x ≤ 2. При x ≤ 0 оно не имеет решений, т.к. , итак, решения неравенства содержится в промежутке 0 x ≤ 2. Возводя неравенство с обеими положительными частями в квадрат, получаем 2 − x x 2 , x 2 + x − 2 > 0 => x x > 1.

Решите графически

Парабола и окружность пересекаются в точках: (-3;4); (0; -5) и (3; 4).

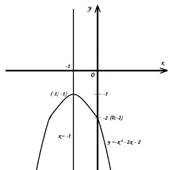
Решить неравенство − x 2 − 2 x −2 y =− x 2 − 2 x −2

Ветви параболы направлены вниз, т.к. a =−1 D = b 2 −4 ac =

= (−2) 2 − 4(−1)∙(−2) = − 4 функция не имеет корней. Находим координаты вершины параболы: ,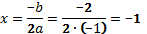

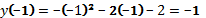
. Уравнение оси симметрии есть x =−1.

С осью Oy парабола пересекается в точке (0; −2).

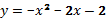
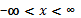
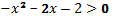
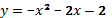
Для всех значениях аргумента функции принимает отрицательные значения => . Если бы мы решали неравенство , то оно не имело бы решений, т.к. не может принимать положительные значения.

Вопросы для закрепления теоретического материала к практическому занятию:

Название практической работы.

Решение заданий практической работы.

Ответы на вопросы для закрепления теоретического материала.

1. Алимов Ш.А. и др. Алгебра и начала математического анализа: Учебник 10—11 классы. — М.И., 2016.

2. Атанасян Л.С., Бутузов В. Ф., Кадомцев С.Б. и др. Математика: алгебра и начала математического анализа. Геометрия. Геометрия (базовый и углубленный уровни). 10—11 классы. — М., 2016.

3. Башмаков М.И. Математика: алгебра и начала математического анализа, геометрия: учебник для студентов профессиональных образовательных организаций, осваивающих профессии и специальности СПО. – М.,2017

4. Башмаков М.И. Математика: алгебра и начала математического анализа, геометрия: Сборник задач профильной направленности: учеб. пособие для студентов профессиональных образовательных организаций, осваивающих профессии и специальности СПО. – М.,2017

5. Башмаков М.И. Математика: алгебра и начала математического анализа, геометрия: Задачник: учеб. пособие для студентов профессиональных образовательных организаций, осваивающих профессии и специальности СПО. – М.,2017

6. Башмаков М.И. Математика: алгебра и начала математического анализа, геометрия: Электронный учеб.- метод. комплекс для студентов профессиональных образовательных организаций, осваивающих профессии и специальности СПО. – М.,2017

Башмаков М.И. Математика: Учебник. — М., 2016