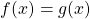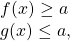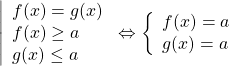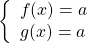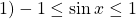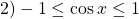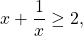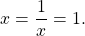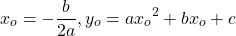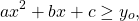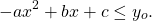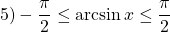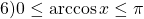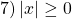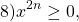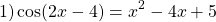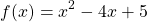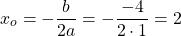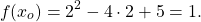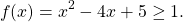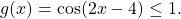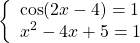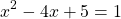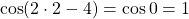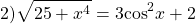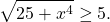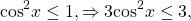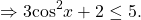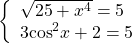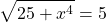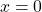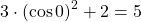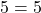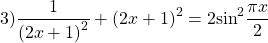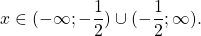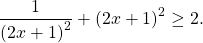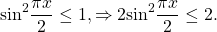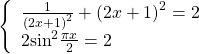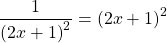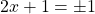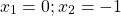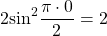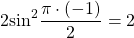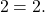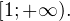Используя метод оценки найдите корни уравнения

Решение уравнений методом оценки

Решение уравнений методом оценки основано на сравнении области значений функций, стоящих в левой и правой части уравнения.

Если в уравнении

то равенство возможно тогда и только тогда, когда и f(x) и g(x) одновременно равны a:

При этом, если максимальное значение функции, стоящей в одной части уравнения, равно минимальному значению функции, стоящему в другой части уравнения, и эти значения достигаются для обеих функций при x=x0, то xo — корень уравнения.

Графически это можно проиллюстрировать так:

Если максимальное значение функции, стоящей в одной части уравнения, равно минимальному значению функции, стоящему в другой части уравнения, но эти значения достигаются при разных x0, то уравнение не имеет корней:

Получив систему уравнений

достаточно решить одно из уравнений (которое проще), а затем проверить, являются ли найденные корни корнями другого уравнения.

Чаще всего при решении уравнений методом оценки правой и левой части используют следующие соображения:

причём равенство достигается при

4) Квадратичная функция в вершине параболы (x0; y0)

при a>0 принимает своё наименьшее значение:

при отрицательном коэффициенте a при x² — наибольшее значение:

где n — натуральное число.

Примеры решения уравнений методом оценки левой и правой части.

— квадратичная функция. График — парабола ветвями вверх. Наименьшее значение принимает в вершине

С другой стороны

Следовательно, исходное уравнение равносильно системе уравнений

Корень второго уравнения:

x=2. Проверяем, является ли 2 корнем первого уравнения:

— верно. Следовательно, x=2 — единственный корень.

Так как x⁴≥0, то 25+ x⁴≥25, а значит,

С другой стороны,

Следовательно, исходное уравнение равносильно системе уравнений

Решаем первое уравнение

Проверяем, является ли x=0 корнем второго уравнения:

— верно. Значит, x=0 — корень данного уравнения.

Так как сумма взаимно-обратных положительных чисел не меньше двух,

Так как сумма положительных взаимно-обратных чисел равна 2, если эти числа равны между собой, то

Проверяем, являются ли эти корни корнями второго уравнения.

Таким образом, исходное уравнение имеет единственный корень x= -1.

Метод оценки области значений

Самостоятельная работа №2

Тема: «Решение уравнений. Способы решения уравнений»

Метод разложения на множители

Суть данного метода в том, чтобы путем равносильных преобразований представить левую часть исходного уравнения, содержащую неизвестную величину в какой-либо степени, в виде произведения двух выражений, содержащих неизвестную величину в меньшей степени. При этом справа от знака равенства должен оказаться ноль. Проще всего уяснить эту идею на конкретном примере.

Пример: решите уравнение методом разложения на множители: 2,5x^2+4x = 0.

Решение. Осуществим разложение на множители (представим исходное выражение в виде произведения). Для этого вынесем переменную x за скобки: x(2,5x+4) = 0.

Произведение равно нулю тогда и только тогда, когда хотя бы один из множителей равен нулю. Следовательно, x=0 или 2,5x+4 =0. Из последнего уравнения получаем: 2,5x = -4 или x=-1,6.

Метод замены переменной

Цель данного метода в том, чтобы удачным образом заменить сложное выражение, содержащее неизвестную величину, новой переменной, в результате чего уравнение принимает более простой вид. Далее полученное уравнение решается относительно новой переменной, после чего происходит возврат к исходной переменной. Все эти идеи проще осознать на конкретном примере.

Решите уравнение методом замены переменной:

Решение. Такие уравнения называются биквадратными. Перепишем его в виде: Введем новую переменную Тогда исходное уравнение примет следующий простой вид: Решая полученное квадратичное уравнение, получаем, что или

Возвращаемся теперь к старой переменной (обратная замена): или Решений у первого уравнения нет, поскольку не существует такого действительного числа, квадрат которого был бы отрицателен. Второе уравнение имеет два корня

Метод оценки области значений

Суть данного метода в сравнении областей значений выражений, входящих в уравнение. Часто такой анализ позволяет легко решать сложные уравнения, содержащие различные выражения (рациональные, тригонометрические, логарифмические, показательные и др.). Разберем это на конкретном примере.

Пример:Решите уравнение, используя метода оценки области значений:

Решение. Рассмотрим функцию Известно, что поэтому Итак, функция может принимать значения только из промежутка

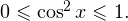
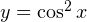
Рассмотрим теперь функцию Графиком данной функции является парабола, ветви которой направлены вверх, а вершина расположена в точке

График соответствующей квадратичной функции

То есть область значений данной функции (те значения, которые может принимать переменная ) представляет собой промежуток

Таким образом выражения, стоящее справа и слева от знака равенства в исходном уравнении, могут оказаться равными, только если их значения окажутся равными 1, причем при одном и том же значении Непосредственной подстановкой убеждаемся, что это условие выполняется при Действительно, и При всех остальных значениях функция больше 1 (см. график). Значит — единственный корень уравнения.

Ответ: 0.

4. Приведение подобных членов.

Переход от уравнения

f(x) + m(x) — m(x) = g(x) (5)

f(x) = g(x) (6),
называют приведением подобных слагаемых.

Прежде чем рассматривать переход от уравнения (5) к уравнению (6), сделаем следующее замечание. Согласно сказанному в предыдущем пункте уравнеПрежде чем рассматривать переход от уравнения (5) к уравнению (6), сделаем следующее замечание. Согласно сказанному в предыдущем пункте уравнение (5) равносильно уравнению

f(x) + m(x) = g(x) + m(x) (7).

Поэтому переход от уравнения (1) к уравнению (2) означает то же самое, что и переход от уравнения (7) к уравнению (2), т. е. во всех рассуждениях уравнение (1) можно заменять равносильным ему уравнением (7). Таким образом, сказанное в этом пункте будет относиться не только к приведению подобных членов в одной части уравнения, но и к вычеркиванию (взаимному уничтожению) одинаковых слагаемых в левой и правой частях. Прежде чем сформулировать общее утверждение, относящееся к переходу от уравнения (1) к уравнению (2) или, что то же самое, от

уравнения (7) к уравнению (2), рассмотрим следующие примеры.

Пример: . слагаемого — х и — 2 получается равносильное уравнение х 4 = х 2 .

5. Умножение обеих частей уравнения на одно и то же выражение.

Переход от уравнения

f(x) = g(x) (8)
к уравнению

f(x) p(x) = g(x) p(x). (9)
называют умножением обеих частей уравнения на одно и тоже выражение.

По поводу этого перехода можно высказать следующие утверждения:

1) Если в каждой точке, где определены обе функции f(x), g(x) определена также и функция p(x) (иначе говоря, Если в каждой точке, где определены обе функции f(x), g(x) определена также и функция p(x)), то уравнение (9) является следствием уравнения (8) или (8) (9)

2) Если в каждой точке, где определены обе функции f(x), g(x) определена также и функция p(x) и в каждой точке указанного множества функция p(x) отлична от нуля, то уравнения (8) и (9) равносильны, т. е. (8) (9).

Заметим, что в общем случае переход от уравнения (9) к уравнению (8) может привести как к появлению посторонних корней, так и к потере корней.

Рассмотрим уравнение x 2 — x = 0. Умножив обе части этого уравнения на , мы получим уравнение = 0, которое не является следствием исходного. В самом деле, исходное уравнение имеет корни х₁ = 0, х₂ = 1, а уравнение = 0 — лишь корень х = 1. Потеря корня связана с тем, что функция — не определена при. х = 0, а как раз это значение х является корнем заданного уравнения.

6. Метод замены неизвестного. Метод замены неизвестного применяется при решении уравнений вида f(g(x)) = 0.

Он основывается на следующей теореме.

Теорема 3. Рассмотрим уравнение f(t) = 0, где t — вспомогательное неизвестное, и пусть t₁, t₂,₃. t_k — все корни уравнения. Тогда для решения уравнения f(g(x)) = 0 достаточно найти все корни каждого из уравнений g(x) = t_m (m = l, 2, . k) и объединить множества корней этих уравнений.

Иначе говоря, f(g(x)) = 0 g(x) = t₁, g(x) = t₂, . g(x) = t_k.

Эта теорема позволяет свести решение уравнения вида f(g(x))= 0 к решению нескольких более простых уравнений f(t) = 0, g(x) = t_k, где k = 1, 2. m.

Обычно эта теорема применяется следующим образом.

Дано некоторое уравнение f(x) = 0. Задача заключается в том, чтобы умело подобрать функцию g(x), позволяющую ввести новое неизвестное t = g(x), и затем выразить функцию f(х) через t, т. е. представить ее в виде f(x) = h(g(x)). В результате данное уравнение запишется в виде h(g(x))= 0, и для его решения можно будет применить доказанную теорему. Такой прием решения уравнений и называется методом замены неизвестного (поскольку вначале решается уравнение f(t) = 0, в котором неизвестное х заменено новым, вспомогательным неизвестным t.

7. Способ сложения

Алгоритм решения системы линейных уравнений с двумя неизвестными способом сложения.

1. Если требуется, путем равносильных преобразований уравнять коэффициенты при одной из неизвестных переменных в обоих уравнениях.

2. Складывая или вычитая полученные уравнения получить линейное уравнение с одним неизвестным

3. Решить полученное уравнение с одним неизвестным и найти одну из переменных.

4. Подставить полученное выражение в любое из двух уравнений системы и решить это уравнение, получив, таким образом, вторую переменную.

Метод оценки в задачах с параметрами

В этой статье мы рассмотрим мощный метод, который применяется, когда в левой и правой частях уравнения или неравенства стоят функции разных типов. Для того чтобы лучше его запомнить, расскажем историю о том, как птичка и рыбка полюбили друг друга.

Еще раз: в левой и правой частях уравнения находятся функции разных типов. Мы помним, что в математике существует 5 типов элементарных функций: степенные, показательные, логарифмические, тригонометрические и обратные тригонометрические. Подробно о них — в статье «Элементарные функции и их графики».

Мы знаем из курса алгебры, что уравнения, которые мы решаем, обычно относятся к одному из этих пяти типов. Показательные и логарифмические, квадратные и тригонометрические уравнения — для каждого типа есть свои характерные приемы и способы решения. И основаны они на тех или иных свойствах функций. Для тригонометрических уравнений — свои способы решения, для логарифмических — свои.

Но сейчас мы рассмотрим уравнение, в левой и правой частях которого находятся функции разных типов. Вот оно:

Такое уравнение бесполезно возводить в квадрат или делать с ним арифметические действия. Бесполезно брать логарифмы от обеих частей — от этого оно станет только хуже.

Что же с ним делать? Упростим его, насколько возможно.

Посмотрим на правую часть этого уравнения. Очевидно,

Интересно — а какой же будет левая часть? Давайте оценим и ее тоже.

Поскольку получим, что

Получается, что при всех значениях х левая часть уравнения не меньше, чем 8, а правая часть не больше, чем 8. И это значит, что решением уравнения могут быть только такие значения переменной х, когда и левая, и правая часть равны 8. Тогда они равны друг другу. В этом и состоит метод оценки.

Метод оценки применяется для уравнений и неравенств, где функции, стоящие в левой и правой части, могут быть равны друг другу только в определенной точке, причем одна из них принимает в этой точке наименьшее значение, а другая — наибольшее.

Вот как это выглядит:

А чтобы лучше запомнить суть метода, рассказываем историю.

Глубоко-глубоко в море жила маленькая рыбка. А высоко-высоко в небе жила маленькая птичка. И однажды они полюбили друг друга! А встретиться они могли только в одной точке, на границе моря и неба, до которой рыбке надо подняться, а птичке — спуститься!

Смотри видео о том, как птичка и рыбка полюбили друг друга и что из этого получилось

О чем эта история? О нашем уравнении, конечно! В левой и правой его частях находятся функции разных типов. И при определенном значении х они оказались равны друг другу. Легко заметить, что значения выражения в левой части всегда больше либо равны восьми («птичка»), значения выражения в правой части — меньше либо равные восьми («рыбка»). И возможно, есть такая точка, где у одной из этих функций будет минимум, а у другой — максимум, причем значение каждой из них станет равно восьми.

Нам осталось только проверить, что эта точка действительно есть. Приравняем правую часть к восьми.

Подставив в левую часть, получим, что и она равна восьми при этом значении x. Значит, является единственным корнем данного уравнения.

Вот еще одна задача на метод оценки.

Умножим обе части данного неравенства на положительную величину:

В левой и правой частях полученного неравенства оказались функции разных типов. Метод оценки!

Выделим под логарифмом полный квадрат:

Неравенство примет вид:

Наибольшее значение выражения под логарифмом равно 2. Стало быть, наибольшее значение логарифма равно
, то есть 1, и достигается оно при единственном значении x = 3.

В то же время, наименьшее значение выражения также равно 1, и достигается оно при том же единственном значении x= 3.

Поэтому последнее неравенство будет выполнено лишь в одном-единственном случае: когда обе его части равны 1, т. е. при x = 3. Решением данного неравенства служит единственное число!

Мы обещали задачи с параметрами, которые решаются методом оценки. Вот, пожалуйста:

18. Найдите все значения а, при которых уравнение

имеет ровно два решения.

Обозначим Уравнение примет вид:

Мы видим, что левая часть этого уравнения не меньше единицы, а правая часть — не больше единицы. Равенство может быть, только если обе они равны единице.

Это классическая задача на метод оценки.

В нашем случае функция f в левой части уравнения и функция g в правой части «встречаются», когда одна из них принимает свое наименьшее значение, равное единице, а другая — свое наибольшее значение, также равное единице.

Второе уравнение означает, что частное — целое число.

В первом уравнении сделаем замену

Обозначим а — 6 = b и найдем, сколько корней имеет уравнение при неотрицательных z и различных b.

Нам нужно, чтобы исходное уравнение относительно х имело два корня.

Это происходит, когда уравнение имеет единственный положительный корень , которому соответствуют и

Заметим, что так как если то и двух корней не получится.

График функции — парабола с вершиной М(3;-9)

1) Если , то уравнение имеет единственный корень , которому соответствуют два корня исходного уравнения: и

Поскольку , в этом случае . Это значение удовлетворяет и второму уравнению системы: — целое.

2) Уравнение > имеет единственное положительное решение также при , при этом и