Исследование эллипса по его уравнению

Исследование формы эллипса по его уравнению

Исследование формы эллипса по его уравнению

Установим форму эллипса, пользуясь его каноническим уравнением.

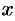
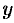
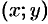
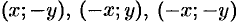
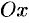
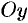
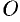
1. Уравнение (11.7) содержит и только в четных степенях, поэтому если точка принадлежит эллипсу, то ему также принадлежат точки . Отсюда следует, что эллипс симметричен относительно осей и , а также относительно точки (0; 0), которую называют центром эллипса.

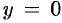
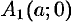
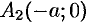
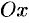
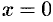
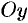
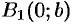
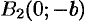
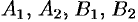
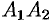
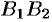
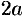
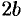
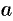
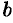
2.Найдем точки пересечения эллипса с осями координат. Положив , находим две точки и , в которых ось
пересекает эллипс (см. рис. 50). Положив в уравнении (11.7) , находим точки пересечения эллипса с осью : и . Точки называются вершинами эллипса. Отрезки и , а также их длины и называются соответственно большой и малой осями эллипса. Числа и называются соответственно большой и малой полуосями эллипса.

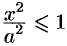
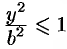
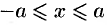
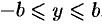
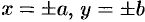
3. Из уравнения (11.7) следует, что каждое слагаемое в левой части не превосходит единицы, т. е. имеют место неравенства и или и . Следовательно, все точки эллипса лежат внутри прямоугольника, образованного прямыми .

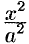
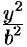
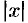
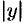
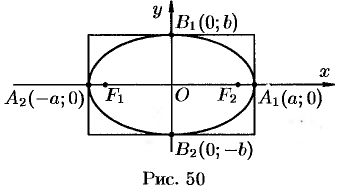
4. В уравнении (11.7) сумма неотрицательных слагаемых и равна единице. Следовательно, при возрастании одного слагаемого другое будет уменьшаться, т. е. если возрастает, то уменьшается и наоборот.

Из сказанного следует, что эллипс имеет форму, изображенную на рис. 50 (овальная замкнутая кривая).

На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:

Другие темы по высшей математике возможно вам они будут полезны:

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

65. Исследование эллипса по каноническому уравнению. Эллипса и окружность. Эксцентриситет эллипса. Параметрические уравнения эллипса

В § 1 доказано, что в канонической системе координат OXy Уравнение эллипса имеет вид:

. (1)

1. Эллипс не проходит через начало системы координат, так как координаты точки О(0,0) не удовлетворяют уравнению (1).

2. Найдем точки пересечения эллипса с осями координат. Для нахождения точки пересечения с осью ОХ полагаем в уравнении (1) У = 0 и находим X = ±A. Таким образом эллипс пересекает ось ОХ В точках A1(-A, 0), A2(A, 0). Аналогично находим, что эллипс пересекает ось ОY В точках B1(0,-B), B2(0, B).

3. Так как все переменные входят в уравнение (1) в четной степени, то вместе с точкой (X, Y) эллипсу принадлежат четыре точки (±X, ±Y) (с произвольными комбинациями знаков). Таким образом, эллипс симметричен относительно, всех координатных осей OX, OY и начала координат. Точка О называется Центром эллипса.

4. Из уравнения эллипса находим, . Отсюда следует, что эллипс ограниченная линия, которая находится в прямоугольнике: —A £ X £ A, —B £ Y £ B (см. рис. 18).

5. Исследуем поведение эллипса в первой четверти. Для этого выразим Y из уравнения (1) через X:

.

Отсюда видим, в первой четверти на отрезке [0, A] эллипс является графиком убывающей функции.

6. Любая прямая, проходящая через начало координат, пересекает эллипс в двух точках. Действительно, вертикальная прямая, ось OY, пересекает эллипс в двух вершинах, любую другую прямую можно задать уравнением Y = Kx, K € R. Подставляя в уравнение (1) находим, что прямая пересекает эллипс в точках , где

Аналитическая геометрия

Исследование формы эллипса по его уравнению

Установим форму эллипса, пользуясь его каноническим уравнением.

1.Уравнение (11.7) содержит х и у только в четных степенях, поэто­му если точка (х; у) принадлежит эллипсу, то ему также принадлежат точки (х;-y), (-х; у), (х; -у). Отсюда следует, что эллипс симметричен относительно осей Ох и Оу, а также относительно точки O(0; 0), которую называют центром эллипса.

2. Найдем точки пересечения эллипса с осями координат. Положив у = 0, находим две точки и , в которых ось Ох пересекает эллипс (см. рис. 28). Положив в уравнении (11.7) x = 0, находим точки пе­ресечения эллипса с осью Оу; и. Точки, на­зываются вершинами эллипса. Отрез­ки и, а также их длины 2а и 2Ь называются соответственно боль­шой и малой осями эллипса. Числа а и b называются

соответственно боль­шой и малой полуосями эллипса.

3. Из уравнения (11.7) следует, что каждое слагаемое в левой части не превосходит единицы, т. е. имеют место

неравенства и или и . Следовательно, все точки эллипса лежат внутри прямоугольника, образованного прямыми x = ±а, у = ±b.

4. В уравнении (11.7) сумма неотрицательных слагаемых иравна единице. Следовательно, при возрастании одного слагаемого другое будет уменьшаться, т. е. если возрастает, то уменьшается и наоборот.

Из сказанного следует, что эллипс имеет форму, изображенную на рис. 28 (овальная замкнутая кривая).

Дополнительные сведения об эллипсе.

Форма эллипса зависит от отношения . При b=a эллипс превраща­ется в окружность, уравнение эллипса (11.7) принимает вид . В качестве характеристики формы эллипса чаще пользуются отношением .

Отношение половины расстояния между фокусами к большой полу оси эллипса называется эксцентриситетом эллипса и обозначается буквой («эпсилон»):

(11.8)

причем , так как . С учетом равенства (11.6) формулу (11.8) можно переписать в виде

и

Отсюда видно, что чем меньше эксцентриситет эллипса, тем эллипс бу­дет менее сплющенным; если положить , то эллипс превращается в окружность.

Пусть М(х;у) — произвольная точка эллипса с фокусамии(см.рис.29).Длины отрезковиназываются фокальными радиусами точ­ки М. Очевидно,

Имеют место формулы

и .

Прямые называются директрисами эллипса. Значение дирек­трисы эллипса выявляется

Теорема 11.1. Если r — расстояние от произвольной точки эллипса до какого-нибудь фокуса, d — расстояние от этой же точки до соответствующей этому фокусу директрисы, то отношение есть постоянная величина, равная эксцентриситету эллипса:

Из равенства (11.6) следует, что а > Ь. Если же а Рассмотрим модель действий на примере решения задач, уравнений. Матриц и прочих заданий по математике. Математика — это именно такой предмет, где изначально ложный метод не позволит Вам найти решение любой задачи, где решение уравнений осуществляется по заранее описанным схемам и методам, а решение матриц осуществляется по четко отработанным алгоритмам.