Курсовая работа на тему «Методика изучения логарифмических уравнений и неравенств.»
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
Министерство просвещения Российской Федерации
Федеральное государственное бюджетное образовательное учреждение высшего образования «Чеченский государственный
Геометрии и методики преподавания математики
по дисциплине: «Методика обучения математики» .
на тему: «Методика изучения логарифмических уравнений и неравенств»
Выполнена студенткой 4 курса МИ1 группы
очной формы обучения
Профиль «Математика» и «Информатика»
__________ Тепсуркаева Хава Адаовна
Подпись ФИО студента
(Ученая степень и звание)
___________ Багашева Аймани Бураевна
подпись ФИО руководителя
Работа защищена «___» _________2021г. протокол №______
ГЛАВА 1. ЛОГАРИФМИЧЕСКИЕ УРАВНЕНИЯ И НЕРАВЕНСТВА В ШКОЛЬНОМ КУРСЕ МАТЕМАТИКИ……………………………………. 5
1.1. Методические особенности изучения логарифмических уравнений и неравенств…..………………………………………………………….………….5
1.2. Анализ заданий на решение логарифмических уравнений в составе ЕГЭ……………………………………………………………………………..…..8
ГЛАВА 2. ВИДЫ ЛОГАРИФМИЧЕСКИХ УРАВНЕНИЙ И НЕРАВЕНСТВ И МЕТОДЫ ИХ РЕШЕНИЯ……………………………….11
2.1. Метод решения по определению логарифма………………..…………..11
2.3. Метод замены переменной………………………………………..……. 13
2.5. Метод логарифмирования обеих частей уравнения……………..……. 16
2.6. Метод приведения логарифмов к одному и тому же основанию……….17
Актуальность работы. В школьном курсе математики важное место занимает решение показательных и логарифмических уравнений и неравенств. В зависимости от авторов учебника эта тема изучается в 10 или 11 классе. Показательные и логарифмические уравнения, неравенства встречаются в заданиях ЕГЭ. Поэтому, изучению методов решения показательных и логарифмических уравнений и неравенств должно быть уделено особое внимание. Из вышеуказанного следует актуальность выбранной темы, необходимость рассмотрения этой темы для будущего учителя математики.
При решении логарифмических уравнений часто возникают трудности, связанные со следующими особенностями:
— незнание четкого алгоритма решения логарифмических уравнений;
— при решении логарифмических уравнений, ученики производят преобразования, которые не равносильны исходным уравнениям;
— при решении логарифмического уравнения введением новой переменной забывают возвращаться к обратной замене.
Цель данной работы: изучить теоретический материал по теме «Логарифмические уравнения в школьном курсе», провести анализ этой темы в учебниках алгебра и начала анализа, рассмотреть основные методы решения логарифмических уравнений, систематизировать и обобщить основные особенности этой темы.
Для достижения поставленной цели необходимо решить следующие задачи:
— изучить требования государственных стандартов по теме «Логарифмические уравнения»;
— проанализировать материал по теме в учебниках алгебры и начала анализа;
— систематизировать методы решения логарифмических уравнений;
— систематизировать и обобщить методические особенности изучения данной темы.
Объектом исследования является процесс обучения математики в старших классах.
Предметом исследования являются методические особенности изучения показательных и логарифмических уравнений, неравенств.
− анализ психолого-педагогической литературы по проблеме исследования;
− методы статистической обработки полученной информации.
Структура работы : введение, две главы, заключение, список литературы. Объем работы: 27 стр.
ГЛАВА 1. ЛОГАРИФМИЧЕСКИЕ УРАВНЕНИЯ И НЕРАВЕНСТВА В ШКОЛЬНОМ КУРСЕ МАТЕМАТИКИ.
1.1 Методические особенности изучения логарифмических уравнений и неравенств.
Первоначально в курсе алгебры изучались такие функции, вычисление значений которых сводилось к четырем арифметическим действиям и возведению в степень. Для вычисления значений логарифмической функции нужно уметь находить логарифмы чисел, т.е. выполнять новое для учащихся действие – логарифмирование. До появления компьютеров логарифмы широко использовались для выполнения вычислений и детально изучались в школе. Теперь же их роль стала вспомогательной, а изучение в школе не стало столь подробным.
Знакомство с логарифмами чисел и их свойствами для многих учащихся достаточно сложно. Поэтому полезны подробные и наглядные объяснения. Обычно логарифм определяется как показатель степени, в которую нужно возвести основание, чтобы получить данное число: 
, т.к. 
. Следует обратить внимание на то, что является корнем уравнения 
, а поэтому 
. Таким образом, получается основное логарифмическое тождество 
, где 
Это равенство является краткой символической записью определения логарифма.
Доказательство свойств логарифма опирается на его определение. Т.к., например, по определению логарифма 
, 
, то, перемножая эти равенства и используя свойство умножения степеней, получаем 
, 
. Последнее равенство показывает, что 
отсюда и следует свойство логарифма произведения 
На практике рассматриваются логарифмы по различным основаниям, в частности по основанию 10 ( 
десятичный логарифм) и по основанию 
( 
— натуральный логарифм), отсюда возникает необходимость формулы перехода от логарифма по одному основанию к логарифму по другому основанию: 
, где 
Т.к. на микрокалькуляторе есть клавиши 
и 
, то для вычисления логарифма по основаниям, отличным от 10 и , нужно использовать формулу перехода.
Уравнение, содержащее неизвестное под знаком логарифма или в его основании, называется логарифмическим уравнением.
Простейшим логарифмическим уравнением является уравнение вида
(1)
Утверждение 1. Если 
, уравнение (1) при любом действительном b имеет единственное решение 
Пример 1 . Решить уравнения:
Решение. Используя утверждение 1, получим
Приведем основные свойства логарифма.
. Основное логарифмическое тождество:
где 
Логарифм произведения положительных сомножителей равен сумме логарифмов этих сомножителей:
Замечание. Если 
тогда свойство 
примет вид
Логарифм частного двух положительных чисел равен разности логарифмов делимого и делителя:
Замечание. Если 
, тогда свойство 
примет вид
, 
Логарифм степени положительного числа равен произведению показателя степени на логарифм этого числа:
. Формула перехода к другому основанию:
, 
в частности, если 
, получим 
, 
Используя свойства 
, легко получить следующие свойства
и, если в (5) c — четное число 
), имеет место
[1 c .214]
Перечислим и основные свойства логарифмической функции 
:
1. Область определения логарифмической функции есть множество положительных чисел.
2. Область значений логарифмической функции — множество действительных чисел.
3. При 
логарифмическая функция строго возрастает 
а при 
, — строго убывает 
4. 
5. Если , то логарифмическая функция отрицательна при x (0;1) и положительна при 
а если , то логарифмическая функция положительна при 
и отрицательна при 
.
6. Если 
то логарифмическая функция выпукла вверх, а если 
— выпукла вниз [1 c .217].
Важнейшей частью школьного курса математики является обучение методам решения уравнений. Для успешного решения уравнений необходимо знать и использовать свойства показательной и логарифмической функций, свойства действий со степенями, определение логарифма, основные логарифмические тождества.
Цель темы – обучение учащихся методам решения логарифмических уравнений.
Для передачи теоретического материала наиболее эффективна исследовательская работа учеников, которая сопровождается беседами учителя с учащимися. Для закрепления материала используются задания из учебника, дополнительной литературы.
Особое место отводится самостоятельной работе – решению уравнений, подготовка сообщений, проработке теоретического материала. При изучении темы «логарифмические уравнения» учащиеся должны уметь:
1. Определять методы решения логарифмических уравнений.
2. Решать логарифмические уравнения.
1.2 Анализ заданий на решение логарифмических уравнений в составе ЕГЭ.
Рассмотрим задания из состава ЕГЭ, содержащие примеры на решение логарифмических выражений уравнений:
1. Найдите корень уравнения 
.
2. Найдите корень уравнения 
Ответ : 21.[2 c .40]
3. Решите уравнение 
Если, уравнение имеет более одного корня, в ответе укажите меньший из них.
На ОДЗ перейдем к уравнению на основание логарифма:
Итак, на ОДЗ уравнение имеет только один корень.
4. а) Решите уравнение 
.
б) Укажите корни этого уравнения, принадлежащие отрезку 
.
а) Запишем исходное уравнение в виде:
б) Поскольку 
отрезку принадлежит единственный корень −2.
Ответ : а) −2; 1, б) −2.
5. а) Решите уравнение 
б) Укажите корни этого уравнения, принадлежащие отрезку 
.
а) Из уравнения получаем:
б) Заметим, что 
.
Значит, указанному отрезку принадлежит только корень −2.
Ответ: а) −2 и 16; б) −2. [2 c.30]
Анализируя задания ЕГЭ, можно сделать вывод о том, что задачи на решение логарифмических уравнений могут встречаться в любой части заданий ЕГЭ. В первойчасти обычно предлагают решить простейшие логарифмические уравнения. Во второй части можно встретить более сложные логарифмические уравнения, решение которых обычно является одним из этапов выполнения задания. Уравнения в части «С» могут быть и комбинированные, т.е. быть логарифмическими, иррациональными, тригонометрическими и показательными и т.д.
В части «С» предложены не только логарифмические уравнения, но и системы уравнений. Задание «С-1» заключается в том, чтобы решить уравнение и выбрать подходящий корень из определенного промежутка [10 c .162].
ГЛАВА 2. ВИДЫ ЛОГАРИФМИЧЕСКИХ УРАВНЕНИЙ И НЕРАВЕНСТВ И МЕТОДЫ ИХ РЕШЕНИЯ.
2.1. Метод решения по определению логарифма
Решение уравнений, основанных на определении логарифма.
Пример 1 
Решение: По определению логарифма
корень уравнения.
Ответ: 
ОДЗ 
Используем определение логарифма:
Ответ: 
2.2. Метод потенцирования
Решение логарифмических уравнений типа 
сводится к решению уравнения 
Это следует из монотонности логарифмической функции.
Потенцирование — это переход от уравнения вида к уравнению 
, где 
— отличное от единицы положительное число, 
— элементарные алгебраические функции, 
Для решения рассматриваемого типа уравнений достаточно найти все решения уравнения 
.Среди полученных выбрать те, которые принадлежат ОДЗ уравнения 
В случае, если уравнение решений не имеет, то их не имеет и исходное логарифмическое уравнение.[3 c .168]
принадлежит интервалу 
значит, является корнем исходного логарифмического уравнения.
Ответ: 
значит, −5,5 не является корнем исходного уравнения.
Ответ: 
[4 c .87].
2.3. Метод замены переменной
Уравнения вида 
решаются с помощью подстановки 
, которая приводит уравнение к виду 
Если t — корень уравнения 
, то после возвращения к подстановке можно найти корень исходного логарифмического уравнения, т. е. 
(аналогично находятся и другие корни, если они есть) [1 c .219].
оба принадлежат ОДЗ.
Пример: 
Обозначив 
получим уравнение 
Корни этого уравнения 
Из уравнения 
находим, что 
а из уравнения 
=2 следует, что 
Оба корня принадлежат ОДЗ: 
Пример: 
Введём новую переменную:
Вернёмся к обозначенному:
Первый корень не принадлежит ОДЗ, а значит, решением является
Ответ: 
[4 c .89].
2.4. Графический метод
Метод основан на использовании графических иллюстраций или каких-либо свойств функций.
В одной системе координат строим графики функций, записанные в левой и в правой частях уравнения, затем находим точку (точки) их пересечения. Абсцисса найденной точки является решением уравнения.
· левую и правую части уравнения представить в виде функций;
· построить графики обеих функций в одной системе координат;
· найти точки пересечения графиков, если они есть;
· указать абсциссы точек пересечения, это корни уравнения [3c. 118]
Пример . 
(обратить внимание на несовершенность этого способа)
Р
 |
ис.1
2.5. Метод логарифмирования обеих частей уравнения
Уравнения вида 
решаются логарифмированием обеих частей уравнения.
Логарифмирование — это переход от уравнения к уравнению
Рассмотрим на примерах.
Пример: 
Прологарифмируем обе части уравнения по основанию 2:
Ответ:
Пример: 
Прологарифмируем обе части по основанию 3:
Пусть 
По теореме Виета
Вернёмся к обозначенному
значения принадлежат ОДЗ.
Ответ: 
.
2.6. Метод приведения логарифмов к одному и тому же основанию
Решение: Приведем все логарифмы к основанию 2, по формуле перехода находим: 
, аналогично 
.
Ответ: 
ОДЗ 
Пусть 
Тогда 
Отвеет: 
.
2.7. Методическая разработка урока по теме «Решение логарифмических уравнений»
План — конспект урока по теме:
«Решение логарифмических уравнений»
Цель урока: повторить понятие и свойства логарифма; изучить способы решения логарифмических уравнений и закрепить их при выполнении упражнений.
— обучающие: повторить определение и основные свойства логарифмов, уметь применять их в вычислении логарифмов, в решении логарифмических уравнений;
-развивающие: развить память, внимание, умение работать самостоятельно;
-воспитательные: воспитывать настойчивость, самостоятельность; прививать интерес к предмету.
Тип урока: урок изучения нового материала.
Педагогические технологии: информационно-коммуникационные, коллективная система обучения – вариационная пара.
Необходимое техническое оборудование: компьютер, проектор, экран.
Структура и ход урока:
I. Организационный момент.
Проверка готовности обучающихся и кабинета к занятию. Объявление темы.
Закрепление понятия логарифма, повторение его основных свойств и свойств логарифмической функции:
1. Разминка по теории :
1. Дайте определение логарифма.
2. От любого ли числа можно найти логарифм?
3. Какое число может стоять в основании логарифма?
4. Функция 
является возрастающей или убывающей? Почему?
5. Какие значения может принимать логарифмическая функция?
6. Какие логарифмы называют десятичными, натуральными?
7. Назовите основные свойства логарифмов.
8. Можно ли перейти от одного основания логарифма к другому? Как это сделать?
2. Работа по карточкам :
Вычислить: 
Вычислить: 
3. Фронтальный опрос класса (сопровождается слайдами презентации)
ЕГЭ 2009. Математика. Справочник / А. М. Титаренко, И.
В. Третьяк, Т. М. Виноградова. – М: Эксмо, 2018. – 448 с.
3. Алгебра и начала анализа: Учеб. для 10–11 кл. общеобразовательных учреждений /А.Н. Колмогоров, А.М. Абрамов, Ю.П. Дудницын и др.; Под. ред. А.Н. Колмогорова. – М.: Просвещение, 2014.
4. Дидактические материалы по алгебре и началам анализа для 11 класса /Б.М. Ивлев, С.М. Саакян, С.И. Шварцбурд. – М.: Просвещение, 2013. – 143 с.
5. Система тренировочных задач и упражнений по математике./ Симонов А.Я., Бакаев Д.С., Эпельман А.Г. и др. – М.:Просвещение, 2015. – 208 с.
6. Мордковича А.Г. Алгебра и начала анализа. 10-11 классы: задачник /А.Г. Мордкович, Т.Н. Мишустина, Е.Е. Тульчинская.-М.: Мнемозина, 2017. – 315 с.
7. Алгебра и начала математического анализа. 10-11 классы: учебник для общеобразовательных учреждений: базовый уровень/ Ш.А. Алимов, Ю.М. Колягин, М.В. Ткачева и др., 2012. – 464 с.
8. ЕГЭ – 2012. Математика: типовые экзаменационные варианты: 30 вариантов/ под редакцией А.В. Семенова, И.В. Ященко. – М.: Национальное образование, 2015. – 192 с.
9. Алгебраический тренажер: пособие для школьников и абитуриентов/ под редакцией Мерзляк А.Г., Полонский В.Б., Якир М.С.
– М.: Илекса, 2017. – 320 с.
10. Математика. Репетитор. ЕГЭ-2009. Авторы: В.В.Кочагин; М.Н.Кочагина. — М.: Эксмо, 2019. – 272 с.
11. Тригонометрические, показательные и логарифмические уравнения и неравенства: учебное пособие/ Севрюков П.Ф., Смоляков А.Н. М.: Илекса; Народное образование; Ставрополь: Сервисшкола, 2018. – 352 с.
12. Математика для поступающих в вузы: учебное пособие/ И.Ф. Шарыгин. М.: Дрофа, 2016. – 479 с.
13. Повторяем и систематизируем школьный курс алгебры и начал анализа. – М.: Просвещение, 2017. – 416 с.
Решение логарифмических уравнений и неравенств
Описаны различные способы решения логарифмических уравнений и неравенств и показано их применение
Просмотр содержимого документа
«Решение логарифмических уравнений и неравенств»
ПРОЕКТ на тему: «Решение логарифмических уравнений и неравенств»
Яралиева Б.С. преподаватель математики «Дербентского профессионально- -педагогического колледжа»
Введение……………………………………………………………………3 Глава 1. Теоретические основы. 1.1. Основные понятия…………………………………………………….4
1.2. Методы решения логарифмических уравнений и неравенств…. 7
Глава 2. Применение методов на практике.
2.1.Решение логарифмических уравнений…………………………..…..10
2.2.Решение логарифмических неравенств……………………………. 13
Тема проекта: «Решение логарифмических уравнений и неравенств»
Актуальность: — учащиеся не обладают достаточными знаниями о методах решения логарифмических уравнений и неравенств;
— в материалах ЕГЭ встречаются задания, содержащие логарифмические уравнения и неравенства.
Цель: сформировать у учащихся умение решать различного типа логарифмические уравнения и неравенства для успешной сдачи ЕГЭ.
Задачи: собрать и изучить теоретический материал по способам решения логарифмических уравнений и неравенств; описать различные способы их решений и показать учащимся применение рассмотренных методов на примерах.
Объект исследования: процесс обучения учащихся решению логарифмических уравнений и неравенств на уроках математики.
Предмет исследования: методы решения логарифмических уравнений и неравенств.
Гипотеза исследования основана на предположении о том, что знание различных методов решения логарифмических уравнений и неравенств может повысить эффективность изучения данной темы и качество подготовки обучающихся к сдаче ЕГЭ.
Методы исследования: изучение специализированной литературы, анализ, сравнение, применение теоретических знаний при решении практических задач.
Выборка исследования: различные методы решений логарифмических уравнений и неравенств.
Глава 1. Теоретические основы. 1.1. Основные понятия.
- Логарифмы и их свойства
Рассмотрим уравнение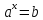 
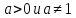
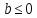
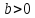
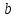
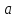
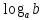
, при 
. При 
это уравнение не имеет решений и при 
имеет единственное решение. Данное решение называют логарифмом 
по основанию 
и обозначают 
.
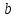
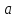
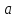
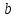
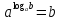
Логарифмом числа по основанию называется показатель степени, в которую необходимо возвести число, чтобы получилось число:
.
Это равенство называют основным логарифмическим тождеством
При .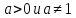 
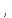
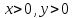
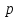
и действительном 
имеют место равенства:
1. 
;
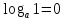
2.
;
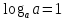
3. 
;
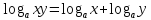
4.
;
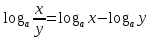
5.
.
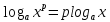
Формула перехода к новому основанию:
Имеет место тождество
.
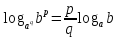
Из него следуют следующие равенства:
, 
.
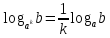
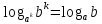
Так же имеет место равенство
Логарифм, основанием которого является число 10, называют десятичным логарифмом и обозначают . Логарифм, основанием которого является число e, называют натуральным логарифмом и обозначают .
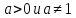
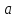
Функцию вида , где называют логарифмической функцией с основанием .
Основные свойства логарифмической функции:
1. Область определения логарифмической функции есть множество положительных вещественных чисел — R+.
2. Область значения логарифмической функции есть множество вещественных чисел.
3. Если основание логарифмической функции , то функция возрастает на всей области определения. Если же для основания логарифмической функции имеет место неравенство , то логарифмическая функция убывает на всей области определения.
4. График логарифмической функции всегда проходит через точку (1;0).
5. Возрастающая логарифмическая функция положительна при и отрицательна при .
6. Убывающая логарифмическая функция отрицательна при и положительна при .
График возрастающей логарифмической функции — ( ):
График убывающей логарифмической функции — ( ):
7. Функция не является четной или нечетной. Логарифмическая функция – функция общего вида.
8. У функции нет точек максимума и минимума.
Графики показательной и логарифмической функций с одинаковыми основаниями симметричны относительно прямой .
Логарифмические уравнения и неравенства.
Логарифмическим уравнением называется уравнение, содержащее неизвестное под знаком логарифма или (и) в его основании.
Простейшим логарифмическим уравнением является уравнение вида
Логарифмическим неравенством называется неравенство, содержащее неизвестное под знаком логарифма или (и) в его основании.
1.2. Методы решения логарифмических уравнений и неравенств.
При решении логарифмических уравнений используют различные методы. Выбор метода зависит от вида уравнения. Перечислим некоторые из них:
Использование определения логарифма
Потенцирование (переход от логарифма данного выражения к самому этому выражению).
Приведение к одному основанию.
Введение новой переменной.
Логарифмирование обеих частей уравнения.
Для решения логарифмических неравенств часто используются следующие утверждения относительно равносильности неравенств и учитываются свойства монотонности логарифмической функции.
1. Если a 1, то неравенство равносильно системе неравенств
2. Если 0 a равносильно системе неравенств
3. Неравенство равносильно совокупности систем неравенств
4. Знак совпадает со знаком в ОДЗ.
5. Знак разности совпадает со знаком произведения в ОДЗ.
В работе использовала следующие источники:
- И.В. Яковлев Логарифмические уравнения и неравенства. Материалы по математике. MathUs.ru
- Башмаков М.И. Математика 2012 г.
- В.Г. Рисберг, И.Ю.Чернилова Решение показательныч и логарифмических уравнений, неравенств и систем уравнений повышенного и высокого уровня сложности. Учебное пособие. 2015 г.
- Шувалова Э.З., Агафонов Б.Г., Богатырев Г.И. Повторим математику.
5.Эфендиев Э.И.- Практикум по элементарной математике-2015 г.
6. Колмогоров А.Н.- Алгебра и начала анализа.-2013 г. (учебник 10-11кл)
В источниках [1], [3] очень хорошо раскрыт метод рационализации, суть которого высказана у нас в утверждениях 4 и 5.
В источниках [4], [5], [6] приведены задания, во всей полноте характеризующие тот или иной метод решения логарифмических уравнений и неравенств.
Из источника [3] взяты задания повышенного уровня.
Проанализировав материал школьных учебников по алгебре и началам математического анализа для 10 – 11 классов, могу сделать вывод о недостаточном освещении изучаемого вопроса в учебно-методической литературе. Это затрудняет работу учителя при изучении данной темы и подготовке к сдаче ЕГЭ.
В источниках [6], [2] при рассмотрении темы «Решение логарифмических уравнении и неравенств» приведены лишь методы решения уравнений с использованием определения логарифма, потенцирования и перехода к одному основанию. А ведь есть и другие методы. Знание различных методов облегчило бы учащимся выполнение заданий с логарифмическими уравнениями. Надо учитывать, что задания в материалах ЕГЭ сложнее заданий в школьных учебниках (задания С). Так же обстоит дело с решением логарифмических неравенств. Метод рационализации намного упростил бы их решение. Он позволяет в определённых случаях упростить неравенство и свести его к рациональному неравенству (которое решается методом интервалов).
Выводы: изучаемая нами тема в различных источниках преподносится в разной последовательности и форме.
Глава 2. Применение методов на практике.
2.1.Решение логарифмических уравнений.
Рассмотрим применение приведенных методов при решении логарифмических уравнений.
Логарифмические уравнения и неравенства
Логарифмическим уравнениям и неравенствам в вариантах ЕГЭ по математике посвящена задача C3. Научиться решать задания C3 из ЕГЭ по математике должен каждый ученик, если он хочет сдать предстоящий экзамен на «хорошо» или «отлично». В данной статье представлен краткий обзор часто встречающихся логарифмических уравнений и неравенств, а также основных методов их решения.
Итак, разберем сегодня несколько примеров логарифмических уравнений и неравенств, которые предлагались учащимся в вариантах ЕГЭ по математике прошлых лет. Но начнет с краткого изложение основных теоретических моментов, которые нам понадобятся для их решения.
Логарифмическая функция
Определение
0,\, a\ne 1 \]» title=»Rendered by QuickLaTeX.com»/>
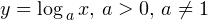
называют логарифмической функцией.
Основные свойства
Основные свойства логарифмической функции y = loga x:
| | a > 1 | 0 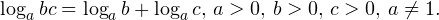 0,\, b>0,\, c>0,\, a\ne 1. \]» title=»Rendered by QuickLaTeX.com»/>• Логарифм частного двух положительных чисел равен разности логарифмов этих чисел:
• Если a и b — положительные числа, причем a ≠ 1, то для любого числа r справедливо равенство:
• Если a, b, c — положительные числа, причем a и c отличны от единицы, то имеет место равенство (формула перехода к новому основанию логарифма):
Решение логарифмических уравнений и неравенствПример 1. Решите уравнение:
Решение. В область допустимых значений входят только те x, при которых выражение, находящееся под знаком логарифма, больше нуля. Эти значения определяются следующей системой неравенств:
С учетом того, что получаем промежуток, определяющий область допустимых значений данного логарифмического уравнения:
На основании теоремы 1, все условия которой здесь выполнены, переходим к следующему равносильному квадратичному уравнению:
В область допустимых значений входит только первый корень. Ответ: x = 7. Пример 2. Решите уравнение:
Решение. Область допустимых значений уравнения определяется системой неравенств:
Очевидно, что эти два условия противоречат друг другу. То есть нет ни одного такого значения x, при котором одновременно выполнялись бы оба неравенства. Область допустимых значений уравнения является пустым множеством, а значит решений у данного логарифмического уравнения нет. Ответ: корней нет. Обратите внимание, что в этом задании нам вообще не пришлось искать корни уравнения. Достаточно оказалось определить, что его область допустимых значений не содержит ни одного действительно числа. Это одно из преимуществ такой последовательности решения логарифмических уравнений и неравенств (начинать с определения области допустимых значений уравнения, а затем решать его путем равносильных преобразований). Примет 3. Решите уравнение:
Решение. Область допустимых значений уравнения определяется здесь легко: x > 0.
Уравнение принимает вид:
Оба ответа входят в область допустимых значений уравнения, поскольку являются положительными числами. Пример 4. Решите уравнение:
Решение. Вновь начнем решение с определения области допустимых значений уравнения. Она определяется следующей системой неравенств:
Воспользовавшись правилом сложения логарифмов, переходим к равносильному в области допустимых значений уравнению:
Основания логарифмов одинаковы, поэтому в области допустимых значений можно перейти к следующему квадратному уравнению:
Первый корень не входит в область допустимых значений уравнения, второй — входит. Ответ: x = -1. Пример 5. Решите уравнение:
Решение. Будем искать решения в промежутке x > 0, x≠1. Преобразуем уравнение к равносильному:
Оба ответа входят в область допустимых значений уравнения. Пример 6. Решите уравнение:
Решение. Система неравенств, определяющая область допустимых значений уравнения, имеет на этот раз вид: Используя свойства логарифма, преобразуем уравнение к равносильному в области допустимых значений уравнению:
Используя формулу перехода к новому основанию логарифма, получаем:
В область допустимых значений входит только один ответ: x = 4. Перейдем теперь к логарифмическим неравенствам. Это как раз то, с чем вам придется иметь дело на ЕГЭ по математике. Для решения дальнейших примеров нам потребуется следующая теорема: Теорема 2. Если f(x) > 0 и g(x) > 0, то: Решение. Начнем с определения области допустимых значений неравенства. Выражение, стоящее под знаком логарифмической функции, должно принимать только положительные значения. Это значит, что искомая область допустимых значений определяется следующей системой неравенств:
Так как в основании логарифма стоит число, меньшее единицы, соответствующая логарифмическая функция будет убывающей, а потому равносильным по теореме 2 будет переход к следующему квадратичному неравенству:
Окончательно, с учетом области допустимых значений получаем ответ:
Пример 8. Решите неравенство:
Решение. Вновь начнем с определения области допустимых значений:
На множестве допустимых значений неравенства проводим равносильные преобразования:
После сокращения и перехода к равносильному по теореме 2 неравенству получаем:
С учетом области допустимых значений получаем окончательный ответ:
Пример 9. Решите логарифмическое неравенство:
Решение. Область допустимых значений неравенства определяется следующей системой:
Видно, что в области допустимых значений выражение, стоящее в основании логарифма, всегда больше единицы, а потому равносильным по теореме 2 будет переход к следующему неравенству:
С учетом области допустимых значений получаем окончательный ответ:
Пример 10. Решите неравенство:
Решение. Область допустимых значений неравенства определяется системой неравенств:
I способ. Воспользуемся формулой перехода к новому основанию логарифма и перейдем к равносильному в области допустимых значений неравенству:
Неравенство будет равносильно двум системам. Первой:
Итак, окончательный ответ:
II способ. Решаем методом интервалов. Преобразуем неравенство к виду:
Вычтем из знаменателя
С учетом того, что выражения
Множество решений данного неравенства Итак, Итак, что нужно для того, чтобы решать логарифмические уравнения и неравенства?
Главное же требование — это настойчивость в достижении своей цели. Учитесь, тренируйтесь, если нужно — ежедневно, изучайте и запоминайте на примерах основные способы решения неравенств и их систем, анализируйте возникающие ошибки и не допускайте их в будущем. За помощью в этом нелегком деле вы можете обратиться к своему школьному учителю по математике, репетитору, родителям, друзьям и знакомым, книгам, а также огромному количеству материалов, доступных на просторах Интернета. Желаю вам успехов в подготовке к Единому государственному экзамену по математике. источники: http://multiurok.ru/files/reshenie-logarifmicheskikh-uravnenii-i-neravenst-1.html http://yourtutor.info/%D1%80%D0%B5%D1%88%D0%B5%D0%BD%D0%B8%D0%B5-%D0%B7%D0%B0%D0%B4%D0%B0%D1%87-%D1%813-%D0%B5%D0%B3%D1%8D-%D0%BF%D0%BE-%D0%BC%D0%B0%D1%82%D0%B5%D0%BC%D0%B0%D1%82%D0%B8%D0%BA%D0%B5-%D0%BB%D0%BE%D0%B3 |
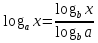
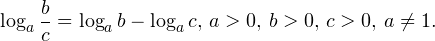0,\, b>0,\, c>0,\, a\ne 1. \]» title=»Rendered by QuickLaTeX.com»/>
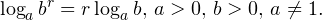0,\, b>0,\, a\ne 1. \]» title=»Rendered by QuickLaTeX.com»/>
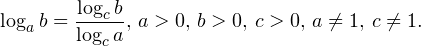0,\, b>0,\, c>0,\, a\ne 1,\, c\ne 1. \]» title=»Rendered by QuickLaTeX.com»/>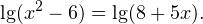
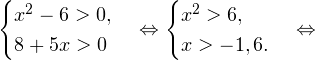0, \\ 8+5x > 0 \end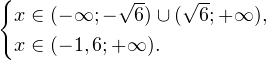 
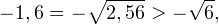-\sqrt<6>, \]» title=»Rendered by QuickLaTeX.com»/>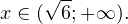
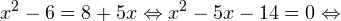
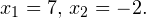
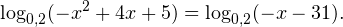
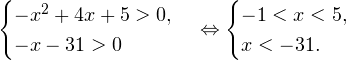0, \\ -x-31>0 \end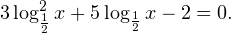
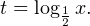
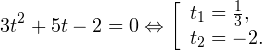
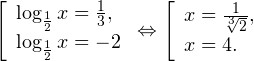
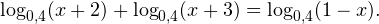
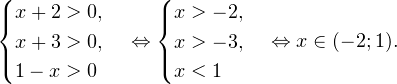0, \\ x+3>0, \\ 1-x>0 \end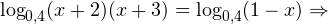
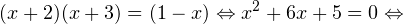
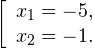
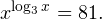
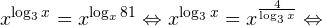
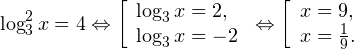
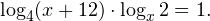
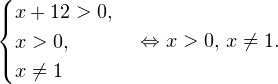0, \\ x>0, \\ x\ne 1 \end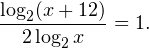
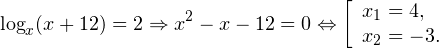
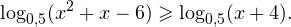
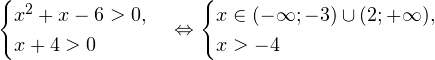0, \\ x+4>0 \end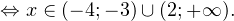
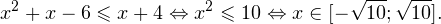
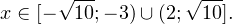
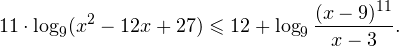
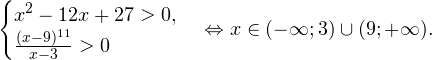0, \\ \frac<(x-9)^<11>>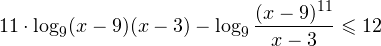
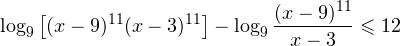
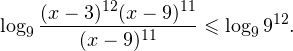
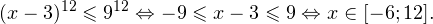
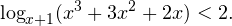
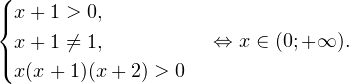0, \\ x+1\ne 1,\\ x(x+1)(x+2)>0 \end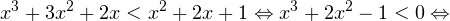
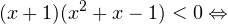
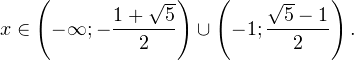
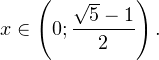
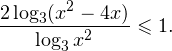
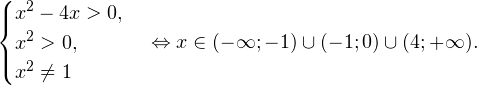0, \\ x^2>0, \\ x^2\ne 1 \end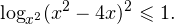
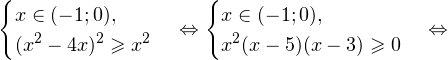
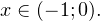
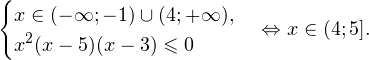
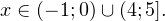
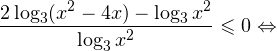
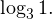Это ничего не изменит, поскольку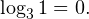 
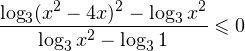
и 
— одного знака при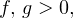 
0,» title=»Rendered by QuickLaTeX.com» height=»18″ width=»74″ style=»vertical-align: -4px;»/> в области допустимых значений имеет место следующий равносильный переход: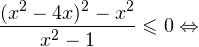
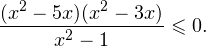
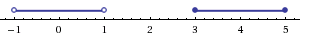
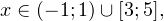а с учетом области допустимых значений получаем тот же результат: 