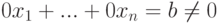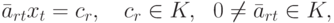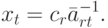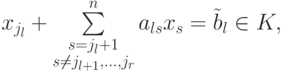Исследование системы линейных уравнений ступенчатого вида

Исследование СЛАУ. Общие сведения

В данной статье мы расскажем о методах, видах, условиях и определениях исследований решений систем линейных уравнений, что такое метод Кронекера-Капели, а также приведем примеры.

Общие сведения (определения, условия, методы, виды)

Системы линейных алгебраических уравнений с n неизвестными могут иметь:

• единственное решение;
• бесконечное множество решение (неопределенные СЛАУ);
• ни одного решения (несовместные СЛАУ).

Пример 1

Система x + y + z = 1 2 x + 2 y + 2 z = 3 не имеет решений, поэтому она несовместна.

Система x + y = 1 2 x + 7 y = — 3 имеет единственное решение x = 2 ; y = 1 .

Система x + y = 1 2 x + 2 y = 2 3 x + 3 y = 3 имеет бесконечное множество решений x = t y = 1 — t при — ∞ t ∞ .

Перед решением системы уравнений необходимо исследовать систему, т.е. ответить на следующие вопросы:

• Совместна ли система?
• Если система совместна, то, какое количество решений она имеет — одно или несколько?
• Как найти все решения?

Если система малоразмерна при m = n , то ответить на поставленные вопросы можно при помощи метода Крамера:

• если основной определитель системы, то система совместна и имеет единственное решение, которое вычисляется методом Крамера;
• если, и один из вспомогательных определителей, то система не является совместной, т.е. не имеет решений;
• если и все, и один из коэффициентов СЛАУ, то система не является определенной и имеет бесконечное множество решений.

Ранг матрицы и его свойства

Бывают случаи, которые выбиваются из представленных вариантов решения СЛАУ, например, линейные уравнения с большим количеством уравнений и неизвестных.

Для такого варианта решения существует ранг матрицы, который представляет собой алгоритм действий в случае решения системы матрицы, когда

В математике выделяют следующие подходы к определению ранга матрицы:

• при помощи понятия линейной зависимости/независимости строк/столбцов матрицы. Ранг равен максимальному количеству независимых строк (столбцов) матрицы
• при помощи понятия минора матрицы в качестве наивысшего порядка минора, который отличается от нуля. Минор матрицы порядка k — определитель k-го порядка, составленный из элементов, которые стоят на пересечении вычеркиваемых k-строк и k-столбцов матрицы;
• при помощи метода Гаусса. По завершении прямого хода ранг матрицы равняется количеству ненулевых строк.

Обозначение ранга матрицы: r ( A ) , r g ( A ) , r A .

Свойства ранга матрицы:

1. квадратная невырожденная матрица обладает рангом, который отличается от нуля;
2. если транспонировать матрицу, то ранг матрицы не изменяется;
3. если поменять местами 2 параллельные строки или 2 параллельных столбца, ранг матрицы не изменяется;
4. при удалении нулевого столбца или строки ранг матрицы не изменяется;
5. ранг матрицы не изменяется, если удалить строку или столбец, которые являются линейной комбинацией других строк;
6. при умножении все элементов строки/столбца на число k н е р а в н о н у л ю ранг матрицы не изменяется;
7. ранг матрицы не больше меньшего из ее размеров: r ( А ) ≤ m i n ( m ; n ) ;
8. когда все элементы матрицы равны нулю, то только тогда r ( A ) = 0 .

Пример 2

А 1 = 1 1 1 2 2 2 3 3 3 , B 1 = 1 0 0 0 0 0

r ( A 1 ) = 1 , r ( B 1 ) = 1

А 2 = 1 2 3 4 0 5 6 7 0 0 0 0 ; В 2 = 1 1 3 1 2 1 4 3 1 2 5 0 5 4 13 6

04. Метод Гаусса

СИстеме линейных уравнений (1) соответствуют три матриц

, .

Первая матрица называется Матрицей системы, вторая — Расширенной или Присойдиненной матрицей системы, третья — Столбцом свободных членов.

Система линейных уравнений называется Системой ступенчатого вида, если расширенная матрица системы есть матрица ступенчатого вида. Неизвестные с коэффициентами неравными нулю, которые стоят первыми в уравнениях системы ступенчатого вида называются Главными неизвестными, а остальные неизвестные называются Свободными.

Линейное уравнение, в котором все коэффициенты равны нулю, а свободный член не равен нулю, т. е. уравнение вида:

,

Не имеет решений. Действительно, если — решение этого уравнения, то получим противоречие с условием. Такое уравнение называем Противоречивым.

Пусть не все уравнения системы (1) нулевые. Тогда и расширенная матрица системы (1) ненулевая. По теореме 2 ее можно конечным числом элементарных преобразований и преобразований выбрасывания нулевой строки можно привести к матрице ступенчатого вида. Полученной матрице соответствует система линейных уравнений ступенчатого вида. Этим преобразованиям расширенной матрицы системы (1) соответствуют такие же преобразования системы линейных уравнений (1). По теореме 1 они переводят систему (1) в равносильную систему линейных уравнений, которая будет являются системой ступенчатого вида.

Таким образом мы доказали первую часть следующей теоремы.

Теорема 3. Любую систему линейных уравнений, содержащую ненулевое уравнение конечным числом элементарных преобразований и преобразований вычеркивания нулевого уравнения можно привести к равносильной ей системе ступенчатого вида. При этом возможны следующие три случая.

1. Если в полученной системе линейных уравнений ступенчатого вида есть противоречивое уравнение, то данная система не имеет решений.

2. Если в полученной системе линейных уравнений ступенчатого вида нет противоречивого уравнения и число уравнений в полученной системе равно числу неизвестных, то данная система имеет единственное решение.

3. Если в полученной системе линейных уравнений ступенчатого вида нет противоречивого уравнения и число уравнений в полученной системе меньше числа неизвестных, то данная система имеет бесконечно много решение.

Доказательство. Пусть дана система (1), содержащая ненулевое уравнение. По выше доказанному, она конечным числом элементарных преобразований она может быть преобразована к равносильной ей системе уравнений ступенчатого вида. Возможны случаи.

В полученной системе ступенчатого вида есть противоречивое уравнение. Тогда ни один набор чисел Не удовлетворяет системе, и система (1) не имеет решений.

В полученной системе ступенчатого вида нет противоречивого уравнения. Тогда в каждом из уравнений системы ступенчатого вида содержится главное неизвестное. Отсюда получаем, что число главных неизвестных, а тем более число всех неизвестных, не менее числа уравнений в системе ступенчатого вида. Тогда возможны под случаи:

В системе ступенчатого вида число уравнений равно числу неизвестных, т. е. система имеет вид:

(12)

Где Все неизвестные в системе являются главными. Из последнего уравнения находим единственное значение для неизвестного : . Подставляя найденное значение в предпоследнее уравнение, находим для неизвестного единственное значение и т. д. Наконец из первого уравнения по найденным значениям неизвестных из первого уравнения находим единственное значение неизвестного . Таким образом, система (12), а поэтому и система (1) имеет единственное решение.

В системе ступенчатого вида число уравнений меньше числа неизвестных. В этом случае матрица полученной системы имеет вид (11), а

Систему можно записать в виде:

(13)

Где В этой системе R главных неизвестных , все остальные Свободные (в системе они обзначены точками. Возьмем для свободных неизвестных произвольные значения. Тогда значения главных неизвестных найдутся однозначно из системы (13). Так как главные неизвестные можно выбрать бесконечным числом способов, то получим, что система (13), а поэтому и система (1) имеет бесконечно много решений.

Следствие. Если в системе однородных уравнений число неизвестных больше числа уравнений, то система имеет бесконечно много решений.

Действительно, система однородных уравнений всегда имеет нулевое решение , и при приведении ее к ступенчатому виду всегда получим систему, в которой число неизвестных больше числа уравнений.

Метод исследования и решения систем линейных уравнений, изложенный в доказательстве теорем 3 называется методом Гаусса.

Пример 1. Решить систему

Составим расширенную матрицу системы и приведем ее к ступенчатому виду:

.

Составим по полученной матрице ступенчатого вида систему линейных уравнений ступенчатого вида:

В полученной системе число уравнений равно числу неизвестных и полученная система имеет единственное решение, которое двигаясь вверх последовательно находим:

Решение системы .

Пример 2. Решить систему

Составим расширенную матрицу системы и приведем ее к ступенчатому виду:

Соответствующая система имеет противоречивое уравнение. Поэтому данная система не имеет решений.

Пример 3. Решить систему

Составим расширенную матрицу системы и приведем ее к ступенчатому виду:

Составим систему ступенчатого вида:

Пусть свободная неизвестная . Тогда находим

Решение системы , где .

Cтупенчатые системы линейных уравнений и метод Гаусса

Исследование ступенчатых систем линейных уравнений

Лемма 3.6.1. Однородная система линейных уравнений всегда совместна.

Доказательство . Решением системы является нулевая строчка .

Лемма 3.6.2. Если система линейных уравнений содержит уравнение

Доказательство . Для любой строчки .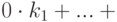

Замечание 3.6.3. Если матрица коэффициентов системы линейных уравнений нулевая (т. е. все коэффициенты равны нулю), то ее совместность равносильна тому, что все свободные члены нулевые (при этом X=K n ).

По ненулевой ступенчатой матрице переменные x₁. x_n разобьем на две группы: главные 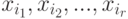, «проходящие» через уголки ступенек (их r штук), и свободные — все остальные n-r переменных (их может и не быть совсем при r=n ).

Замечание 3.6.4. Если в ступенчатой системе линейных уравнений нет «экзотических» уравнений (т. е. если r=m или r и 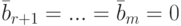), то для любого набора значений для свободных неизвестных существует (и единственный) набор значений для главных неизвестных и эти наборы дают в совокупности решение системы линейных уравнений .

Доказательство . Так как значения для свободных неизвестных заданы, то, рассматривая r -е уравнение и перенося в правую часть уравнения члены со значениями свободных неизвестных, расположенных правее места (r,t) (если они есть), получаем уравнение (см. (3.2))

Теорема 3.6.5 (критерий совместности системы линейных уравнений по ее ступенчатому виду).

1. Система линейных уравнений (a_ij|b_i) из m уравнений с неизвестными x₁. x_n совместна тогда и только тогда, когда в ее ступенчатом виде нет «экзотических» уравнений (т. е. или r=m , или r и ).
2. Для совместной системы свободным неизвестным можно придавать произвольные значения, при этом главные неизвестные однозначно определяются (при заданных значениях свободных неизвестных), тем самым мы получаем все решения системы линейных уравнений.

Доказательство . Отметим, что исходная система и ее ступенчатая системы эквивалентны.

1) а) Ясно, что совместная система не может содержать «экзотическое» уравнение (лемма 3.6.2). Таким образом, при первом появлении «экзотического» уравнения в методе Гаусса процесс надо остановить: система несовместна.

б) Если в ступенчатом виде нет «экзотических» уравнений, то утверждение следует из леммы 3.6.4.

2) Алгоритм нахождения всех решений в случае отсутствия «экзотических» уравнений рассмотрен в лемме 3.6.4.

Следствие 3.6.6. Система линейных уравнений несовместна тогда и только тогда, когда в ее ступенчатом виде найдется «экзотическое» уравнение.

Теорема 3.6.7 (критерий определенности системы линейных уравнений по ее ступенчатому виду). Система линейных уравнений является определенной тогда и только тогда, когда в ее ступенчатом виде:

1. нет «экзотических» уравнений(критерий совместности);
2. r=n (т. е. все неизвестные главные, другим словами — отсутствуют свободные неизвестные).

1. При условии совместности, если r , т. е. имеется хотя бы одно свободное неизвестное, то ему можно придать как минимум два различных значения из поля K . После дополнения значений свободных переменных значениями главных переменных до решения системы мы получаем заведомо два различных решения системы, т. е. |X|>1 , система является неопределенной.
2. Если же при условии совместности r=n , т. е. нет свободных неизвестных, то главные неизвестные определяются в методе Гаусса однозначно (через свободные члены системы), таким образом, система линейных уравнений является определенной.

Упражнение 3.6.8. Процесс приведения к ступенчатому виду можно продолжить на расширенную матрицу системы (a_ij|b_i) . Покажите, что система совместна тогда и только тогда, когда ступенчатый вид расширенной матрицы системы (a_ijb_i) содержит столько же ненулевых строк, сколько и ступенчатый вид матрицы (a_ij) (все лидеры строк ступенчатого вида расширенной матрицы находятся среди столбцов матрицы коэффициентов (a_ij) ).

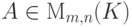
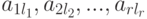
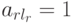
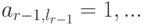
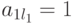
Замечание 3.6.9. Любая ненулевая матрица с помощью элементарных преобразований строк 1-го, 2-го и 3-го типа может быть приведена к главному ступенчатому виду. Действительно, вначале приведем матрицу A к ступенчатому виду. С помощью элементарных преобразований 3-го типа сделаем все лидеры ненулевых строк , , равными единице. После этого, применяя элементарные преобразования строк 1-го типа, добьемся того, что в l_r -м столбце единственный ненулевой элемент — это , затем аналогично добьемся с использованием элементарных преобразований строк 1-го типа того, что единственный ненулевой элемент в l_r-1 -м столбце — это , в l₁ -м столбце — это (эта процедура часто называется обратным ходом метода Гаусса). Таким образом, мы привели матрицу A к главному ступенчатому виду. Позже (см. 9.5.1) будет доказано, что главный ступенчатый вид матрицы определен однозначно.

Если совместная система линейных уравнений (в частности, однородная система) приведена к главному ступенчатому виду, то мы сразу (без последовательной подстановки уже полученных выражений в предыдущие уравнения) получаем единственное выражение главных неизвестных через свободные: l -е уравнение ( 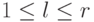) главного ступенчатого вида имеет вид

В частном случае, при r=n , главный ступенчатый вид определенной системы линейных уравнений имеет форму