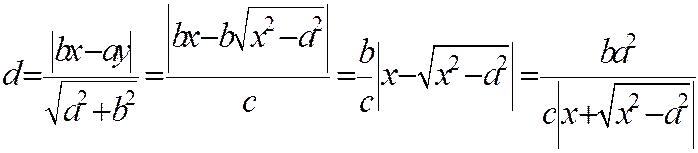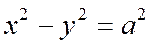Исследование уравнение гиперболы и по

Исследование формы гиперболы

Так как в каноническое уравнение гиперболы координаты х и у входят во второй степени. То оси Ох и Оу являются осями симметрии гиперболы, заданной уравнением: . (1)

а начало координат – центром симметрии.

Из уравнения (1) следует, что

,

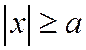
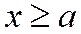
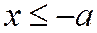
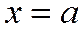
т.е. или , или . Геометрически это означает, что между прямыми и нет ни одной точки гиперболы (1).

Ось симметрии Оу не пересекает гиперболу, заданную уравнением (1), и называется мнимой осью. Ось Ох – пересекает гиперболу (1) в двух точках:

.

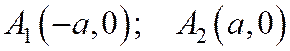
Эта ось называется действительной осью гиперболы. Точки, в которых действительная ось пересекается гиперболу, называются вершинами гиперболы.

Числа а и b в каноническом уравнении называются действительной и мнимой полуосями гиперболы.

Решая уравнение (1) относительно у, беря лишь положительное значение: 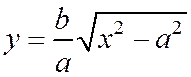(2)

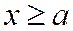
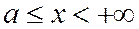
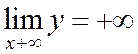
и считая , мы получим точки гиперболы (1), лежащие в первой четверти. Из уравнения (2) следует, что у в полуинтервале есть возрастающая функция; при этом

.

Всякая прямая пересекает гиперболу не более чем в двух точках, так как прямая определяется уравнением первой степени, а гипербола – второй.

Рассмотрим уравнение прямой (3)

Найдем расстояние от точки М(х, у), лежащей на дуге гиперболы, определяемой уравнением (2), до прямой (3); переписывая уравнение (3) в виде , находим:

Отсюда следует, то на полуинтервале расстояние от точки М(х, у) рассматриваемой части гиперболы до прямой (3) есть убывающая функция от х и (рис. 167). Прямая, определяемая уравнением называется асимптотой гиперболы.

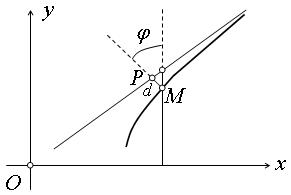
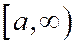
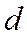
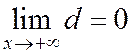
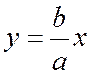
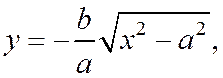
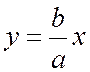
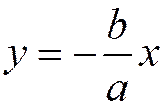
В силу того, что гипербола, заданная каноническим уравнением, симметрична относительно начала координат, расстояние от точки М(х, у), лежащей на дуге гиперболы, заданной уравнением до прямой стремиться к нулю при . Так как гипербола, заданная каноническим уравнением, симметрична и относительно оси Оу, то она имеет вторую асимптоту ,

которая обладает свойством, аналогичным свойству первой асимптоты по отношению к дугам гиперболы, расположенным во второй и четвертой четвертях.

Асимптоты гиперболы являются диагоналями прямоугольника , , , .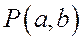

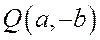
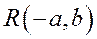
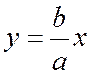
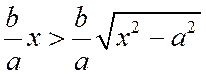
При одной и той же абсциссе х ординаты точки ветви гиперболы, лежащей в первой четверти, с ординатой точки асимптоты связаны неравенством: .

Отсюда и из того, что гипербола симметрична относительно осей координат, следует, что она имеет две ветви, заключенные в двух областях: одна из них ограничена отрезком и продолжениями отрезков и за точки и , другая симметрична этой области относительно мнимой оси гиперболы (рис 168).

Рис.168

Гипербола, у которой полуоси равны, называются равносторонней. Каноническое уравнение равносторонней гиперболы имеет вид

Уравнение асимптот равносторонней гиперболы таковы:

.

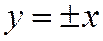
это биссектрисы углов между ее осями симметрии. Асимптоты равносторонней гиперболы взаимно перпендикулярны.

Обратно, если асимптоты гиперболы взаимно перпендикулярны, то ее полуоси равны между собой и, значит гипербола равносторонняя.

ГЛАВА 3. КРИВЫЕ ВТОРОГО ПОРЯДКА

Определение. Пусть на плоскости заданы две точки F1 И F2, расстояние между которыми равно 2C. Пусть, кроме того, задано положительное число A, меньшее C. Гиперболой называется множество точек той же плоскости, для каждой из которых модуль разности расстояний до точек F1 и F2, называемых Фокусами гиперболы, есть число постоянное, равное 2А.

Вывод канонического уравнения

Для вывода уравнения гиперболы, которое мы впоследствии назовём каноническим, выберем на плоскости ортонормированную систему координат следующим образом: ось проведем через фокусы гиперболы, а ось — перпендикулярно ей через середину отрезка F1F2 (рис. 1). Согласно определению, гиперболе удовлетворяют те, и только те точки М плоскости, для которых

. (1)

Чтобы получить уравнение гиперболы остаётся только записать равенство (1) в координатах. В выбранной системе координат фокусы гиперболы имеют следующие координаты: F1 (–C; 0); F2 (C; 0). Координаты произвольной (или текущей) точки множества всегда обозначаются X и Y. Таким образом, M(X; Y). Так как

, ,

То уравнение (1) равносильно следующему:

, (2)

Которое, в свою очередь, равносильно уравнению:

. (3)

Оба эти уравнения являются уравнениями гиперболы, но они имеют громоздкий вид, неудобны для использования и для запоминания, поэтому мы попытаемся их преобразовать к более простому виду. Для этого проведем следующую цепочку преобразований:

(3)

.

Учитывая, что , разделив последнее уравнение на , получаем:

. (4′)

Так как , то , поэтому найдется такое положительное число , что . Теперь уравнение (4′) примет вид:

. (4)

Мы доказали, что если точка принадлежит гиперболе, то её координаты удовлетворяют уравнению (3) или (4).

Докажем обратное: если координаты точки удовлетворяют уравнению (4) или (3), то она принадлежит гиперболе.

<M (X; Y) удовлетворяет (4)>

. (5)

. (6)

Находим разность расстояний:

[(4) ]=

=.

Таким образом, (4) – уравнение гиперболы, которое и называется её Каноническим уравнением.

Исследование формы гиперболы по её каноническому уравнению

1. Симметрия. Так как координаты X И Y В уравнение (4) входят только в чётных степенях, то

<M1(X0; Y0) Г> <M2(–X0; Y0) Г, M3(–X0; –Y0) Г; M4(X0; –Y0)Г>.

Это означает, что гипербола (4) симметрична относительно координатных осей и начала координат. Оси симметрии гиперболы называются Осями гиперболы, центр симметрии – её Центром.

2. Пересечение с осями. Если Y = 0, то (4) <X = ±A>. Значит, гипербола пересекает ось в точках A1 (–A; 0) и A2 = (A; 0), которые называются Вершинами гиперболы. Если же X = 0, то (4) решений не имеет, т. е. ось гипербола не пересекает. Та ось гиперболы, которую она пересекает, называется её Действительной осью, а та, которую не пересекает – Мнимой. Числа A и B называются Полуосями гиперболы, действительной и мнимой соответственно.

3. В силу симметрии гиперболы её достаточно нарисовать в первой координатной четверти, а затем продолжить рисунок по симметрии. Если , , то из (4) можно выразить Y:

. (7)

Если X = A, то Y = 0, если же , то и . Вычислим производную:

.

Если , то , поэтому гипербола в вершине имеет вертикальную касательную.

4. Асимптотами гиперболы (4) называются прямые . Рассмотрим ту из них, которая проходит в первой четверти:

. (8)

Сравнивая (7) и (8), видим, что , значит, гипербола расположена ниже своей асимптоты. Кроме того, ели М – точка гиперболы, Р – точка её асимптоты с такой же первой координатой, — расстояние от М до гиперболы (рис.2), то

.

Следовательно, при неограниченном удалении от начала координат гипербола бесконечно близко приближается к своей асимптоте, не пересекая её.

Теперь можно приступить к рисованию. По обе стороны от начала координат откладываем на действительной оси действительные полуоси, а на мнимой – мнимые. Рисуем прямоугольник, стороны которого проходят через полученные точки параллельно осям координат. Точки пересечения прямоугольника с действительной осью – это вершины гиперболы. Затем проводим диагонали прямоугольника и продляем их – это асимптоты гиперболы. Рисуем гиперболу сначала в первой четверти, начиная от вершины и неограниченно приближая её к асимптоте, а затем продолжаем по симметрии в остальные координатные четверти (рис. 3).

В заключение параграфа отметим, что уравнение задаёт гиперболу, действительной осью которой является ось , а школьное уравнение при — это уравнение гиперболы с перпендикулярными асимптотами, составленное относительно её асимптот.

Определение. Пусть на плоскости заданы две точки F1 И F2, расстояние между которыми равно 2C. Пусть, кроме того, задано число A, большее C. Эллипсом называется множество точек той же плоскости, для каждой из которых сумма расстояний до точек F1 и F2, называемых Фокусами эллипса, есть число постоянное, равное 2А.

Упражнение. По аналогии с выводом канонического уравнения гиперболы получите каноническое уравнение эллипса

, (1)

Где (не забывайте про обратную часть!).

Исследование формы эллипса по его каноническому уравнению

1. Из (1) вытекает, что если точка M(X; Y) принадлежит эллипсу, то , т. е. эллипс полностью лежит внутри этого прямоугольника.

2. Так же как и гипербола, эллипс симметричен относительно обеих координатных осей и относительно начала координат. Оси симметрии эллипса называются Осями эллипса, центр симметрии – его Центром.

3. Если Y = 0, то из (1) следует, что X = ±A, если же X = 0, то Y = ±B. Таким образом, эллипс пересекает обе координатные оси: ось в точках A1(–A; 0), A2(A; 0) (они называются вершинами эллипса), а ось — в точках B1(0; –B), B2(0; B). Числа А и B называются полуосями эллипса, большей и меньшей соответственно.

4. В силу симметрии эллипса его также можно вначале нарисовать только в первой четверти, а затем продолжить по симметрии. Если , то из (1) получаем: . Найдем производную:

.

при , поэтому

Функция убывает на отрезке

Рис. 1. . Так как и , то в точке пересечения эллипса с осью он имеет горизонтальную касательную, а в вершине – вертикальную. Так же, как и у гиперболы, фокусы эллипса находятся в точках F1 (–C; 0) F2 (C; 0). Теперь уже можно эллипс изобразить (см. рис. 1).

Замечание. Уравнение (1) задаёт эллипс, фокусы которого лежат на оси абсцисс при , и лежат на оси ординат при . Если же , то (1) – уравнение окружности радиуса с центром в начале координат. В этом случае C = 0. Таким образом, окружность — это частный случай эллипса с совпадающими фокусами.

Параметрические уравнения эллипса

Пусть задан эллипс своим каноническим уравнением

(1), где . Построим две окружности радиусами и Соответственно с центрами в начале координат. Из начала координат проведем луч под углом к положительному направлению оси , и обозначим А и В точки его пересечения соответственно с большей и меньшей окружностями. Через точку А

Рис. 2. проведём вертикальную прямую, через В – горизонтальную, их пересечение обозначим М. Кроме того, обозначим K и N Основания перпендикуляров, опущенных на ось соответственно из точек А и В (рис.2).

Если точка M имеет координаты (X; Y), то по рис. 2 видно, что

,.

Координаты точки M удовлетворяет (1), значит, она принадлежит эллипсу. Очевидно, если изменяется в пределах от 0 до 2, то мы получим все точки эллипса. Отсюда вытекает один из способов построения точек эллипса. Кроме того, мы вывели его параметрические уравнения:

.

Определение. Пусть на плоскости заданы прямая D и точка F на расстоянии P от неё. Параболой называется множество всех точек той же плоскости, для каждой из которых расстояние до точки F, называемой Фокусом параболы, равно расстоянию до прямой D, называемой её Директрисой.

Вывод канонического уравнения

Выберем на плоскости ортонормированную систему координат следующим образом: ось направим через фокус перпендикулярно директрисе в направлении от неё, ось проведем посредине между фокусом и директрисой параллельно последней. Если — произвольная точка параболы, то определение параболы формально запишется в виде равенства ,

. (1)

С учётом того, что в выбранной системе координат , , , получаем:

(1)

Отсюда и вытекает уравнение параболы

, (2)

Называемое каноническим, а число P в этом уравнении (расстояние от фокуса до директрисы) носит название фокального параметра. Парабола с уравнением (2) отличается от школьной только тем, что в ней переменные и поменялись ролями. Поэтому мы не будем подробно останавливаться на исследовании её формы, а как она выглядит, посмотрите на рис. 2.

§ 4. Эксцентриситет и директрисы эллипса и гиперболы

Определения. Эксцентриситетом гиперболы Называется число e, равное отношению половины расстояния между фокусами гиперболы к её действительной полуоси.

Эксцентриситетом эллипса называется число e, равное отношению половины расстояния между фокусами эллипса к его большей полуоси.

Директрисами гиперболы (эллипса) Называются прямые, перпендикулярные её действительной (большей) оси и отстоящие от центра на расстоянии, равном отношению действительной (большей) полуоси к эксцентриситету.

, (1)

, (1I)

, A > B (2)

, A 1 (e );

3. Если содержит первую степень, то только одной переменной, и тогда свободный член равен нулю ( => );

4. Если свободный член не равен нулю, то он равен 1 или -1.

Кривой второго порядка называется множество точек плоскости, удовлетворяющих какому-либо уравнению 2-й степени.

Теорема. Для любой кривой второго 2-го порядка на плоскости существует ортонормированная система координат, в которой эта кривая задаётся каноническим уравнением.

Эту теорему мы докажем позже, в разделе «Линейная алгебра», а сейчас на основании её мы перечислим всевозможные типы кривых второго порядка. Итак, получаем классификацию кривых второго порядка:

Гипербола и её свойства

Гипербола и её форма.

Гиперболой мы назвали линию, которая в некоторой декартовой прямоугольной системе координат определяется каноническим уравнением
$$
\frac>>-\frac>>=1.\label
$$

Из этого уравнения видно, что для всех точек гиперболы \(|x| \geq a\), то есть все точки гиперболы лежат вне вертикальной полосы ширины \(2a\) (рис. 8.6). Ось абсцисс канонической системы координат пересекает гиперболу в точках с координатами \((a, 0)\) и \((-a, 0)\), называемых вершинами гиперболы. Ось ординат не пересекает гиперболу. Таким образом, гипербола состоит из двух не связанных между собой частей. Они называются ее ветвями. Числа \(a\) и \(b\) называются соответственно вещественной и мнимой полуосями гиперболы.

Рис. 8.6. Гипербола.

Для гиперболы оси канонической системы координат являются осями симметрии, а начало канонической системы — центром симметрии.

Доказательство аналогично доказательству соответствующего утверждения для эллипса.

Для исследования формы гиперболы найдем ее пересечение с произвольной прямой, проходящей через начало координат. Уравнение прямой возьмем в виде \(y=kx\), поскольку мы уже знаем, что прямая \(x=0\) не пересекает гиперболу. Абсциссы точек перечения находятся из уравнения
$$
\frac>>-\fracx^<2>>>=1.
$$
Поэтому, если \(b^<2>-a^<2>k^ <2>> 0\), то
$$
x=\pm \frac<\sqrt-a^<2>k^<2>>>.
$$
Это позволяет указать координаты точек пересечения \((ab/v, abk/v)\) и \((-ab/v, -abk/v)\), где обозначено \(v=(b^<2>-a^<2>k^<2>)^<1/2>\). В силу симметрии достаточно проследить за движением первой из точек при изменении \(k\) (рис. 8.7).

Рис. 8.7. Пересечение прямой и гиперболы.

Числитель дроби \(ab/v\) постоянен, а знаменатель принимает наибольшее значение при \(k=0\). Следовательно, наименьшую абсциссу имеет вершина \((a, 0)\). С ростом \(k\) знаменатель убывает, и \(x\) растет, стремясь к бесконечности, когда \(k\) приближается к числу \(b/a\). Прямая \(y=bx/a\) с угловым коэффициентом \(b/a\) не пересекает гиперболу, и прямые с большими угловыми коэффициентами ее тем более не пересекают. Любая прямая с меньшим положительным угловым коэффициентом пересекает гиперболу.

Если мы будем поворачивать прямую от горизонтального положения по часовой стрелке, то \(k\) будет убывать, \(k^<2>\) расти, и прямая будет пересекать гиперболу во все удаляющихся точках, пока не займет положения с угловым коэффициентом \(-b/a\).

К прямой \(y=-bx/a\) относится все, что было сказано о \(y=bx/a\): она не пересекает гиперболу и отделяет прямые, пересекающие ее, от не пересекающих. Из приведенных рассуждений вытекает, что гипербола имеет вид, изображенный на рис. 8.7.

Прямые с уравнениями \(y=bx/a\) и \(y=-bx/a\) в канонической системе координат называются асимптотами гиперболы.