Исследование уравнений и неравенств с параметром презентация

Презентация Исследование уравнения и неравенства с параметрами.

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

«Актуальность создания школьных служб примирения/медиации в образовательных организациях»

Свидетельство и скидка на обучение каждому участнику

Описание презентации по отдельным слайдам:

Исследование уравнения и неравенства с параметрами.

Цель Более глубоко изучить особенность решение уравнений и неравенств с параметрами, выявить наиболее рационально решение, быстро приводящий к ответу

Задачи Решение линейных уравнений ( и уравнений приводимых к линейным), содержащих параметры Решение линейных неравенств, содержащих параметр.

Уравнение с параметром – это, по сути дела, краткая запись бесконечного семейства уравнений. Каждое из уравнений семейства полу- чается из данного уравнения с параметром при конкретном значении параметра.

Таким образам при создание данного проекта мы усовершенствовали свои знания и нашли для себя что то новое. можно сказать, что эта тема должна изучаться не только на элективных курсах и дополнительных занятиях, но и в школьной программе,

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 952 человека из 80 регионов

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Сейчас обучается 683 человека из 75 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

• Сейчас обучается 313 человек из 70 регионов

Ищем педагогов в команду «Инфоурок»

Дистанционные курсы для педагогов

Самые массовые международные дистанционные

Школьные Инфоконкурсы 2022

33 конкурса для учеников 1–11 классов и дошкольников от проекта «Инфоурок»

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

5 565 269 материалов в базе

Другие материалы

• 19.04.2018
• 2285
• 72

• 19.04.2018
• 4775
• 76

• 19.04.2018
• 1272
• 54

• 19.04.2018
• 639
• 19

• 19.04.2018
• 1089
• 6

• 19.04.2018
• 358
• 3

• 19.04.2018
• 916
• 8

• 19.04.2018
• 318
• 1

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Добавить в избранное

• 19.04.2018 821
• PPTX 630 кбайт
• 15 скачиваний
• Оцените материал:

Настоящий материал опубликован пользователем Дорофеева Марина Владимировна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Автор материала

• На сайте: 6 лет и 4 месяца
• Подписчики: 0
• Всего просмотров: 230099
• Всего материалов: 173

Московский институт профессиональной
переподготовки и повышения
квалификации педагогов

Дистанционные курсы
для педагогов

663 курса от 690 рублей

Выбрать курс со скидкой

Выдаём документы
установленного образца!

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

Тринадцатилетняя школьница из Индии разработала приложение против буллинга

Время чтения: 1 минута

В Египте нашли древние школьные «тетрадки»

Время чтения: 1 минута

В Рособрнадзоре рассказали, как будет меняться ЕГЭ

Время чтения: 2 минуты

Профессия педагога на третьем месте по популярности среди абитуриентов

Время чтения: 1 минута

В России могут объявить Десятилетие науки и технологий

Время чтения: 1 минута

Объявлен конкурс дизайн-проектов для школьных пространств

Время чтения: 2 минуты

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Уравнения и неравенства с параметрами. Выполнила учитель математики МБОУ-СОШ 2 р.п. Степное Советского района Саратовской области Емельянова Н.В. — презентация

Презентация была опубликована 8 лет назад пользователемМарфа Дорожкина

Похожие презентации

Презентация на тему: » Уравнения и неравенства с параметрами. Выполнила учитель математики МБОУ-СОШ 2 р.п. Степное Советского района Саратовской области Емельянова Н.В.» — Транскрипт:

1 Уравнения и неравенства с параметрами. Выполнила учитель математики МБОУ-СОШ 2 р.п. Степное Советского района Саратовской области Емельянова Н.В.

2 « Что за прелесть эти задачи с параметрами! Каждая из них – поэма!» С.А. Тынянкин.

3 Человек, умеющий решать задачи с параметрами, в совершенстве знает теорию и умеет ее применять не механически, а с логикой. Он «понимает» функцию, «чувствует» ее, считает ее своим другом или хотя бы хорошим знакомым, а не просто знает о ее существовании.

4 Что же такое уравнение с параметром? Пусть дано уравнение f (x; a) = 0. Если ставится задача отыскать все такие пары (x; a), которые удовлетворяют данному уравнению, то оно рассматривается как уравнение с двумя равноправными переменными х и а. Но можно поставить и другую задачу, полагая переменные неравноправными. Дело в том, что если придать переменной а какое-либо фиксированное значение, то f (x; a) = 0 превращается в уравнение с одной переменной х, и решения этого уравнения, естественно, зависят от выбранного значения а.

5 Основная трудность, связанная с решением уравнений (и тем более неравенств) с параметром, состоит в следующем: -при одних значениях параметра уравнение не имеет решений; -при других – имеет бесконечно много решений; -при третьих – оно решается по одним формулам; — при четвертых – оно решается по другим формулам. — Если уравнение f (x; a) = 0 нужно решить относительно переменной Х, а под a понимается произвольное действи- тельное число, то уравнение называют уравнением с параметром a.

6 решить уравнение с параметром f (x; a) = 0 – это решить семейство уравнений, получающихся из уравнения f (x; a) = 0 при любых действительных значениях параметра. Уравнение с параметром – это, по сути дела, краткая запись бесконечного семейства урав- нений. Каждое из уравнений семейства полу- чается из данного уравнения с параметром при конкретном значении параметра. Поэтому задачу решения уравнения с параметром можно сформулировать следующим образом:

7 Выписать каждое уравнение из бесконечного семейства уравнений невозможно, но тем не менее каждое уравнение из бесконечного семейства должно быть решено. Сделать это, например, можно, если по некоторому целесообразному признаку разбить множество всех значений параметра на подмножества, а затем заданное уравнение решить на каждом из этих подмножеств. Решение линейных уравнений

8 Чтобы разбить множество значений параметра на подмножества, полезно воспользоваться теми значениями параметра, при которых или при переходе через которые происходит качественное изменение уравнения. Такие значения параметра можно назвать контрольными или особыми. Искусство решения уравнения с параметрами как раз и состоит в том, чтобы уметь находить контрольные значения параметра.

9 Каковы основные типы задач с параметрами?

10 Тип 1. Уравнения, неравенства, их системы, которые необходимо решить либо для любого значения параметра, либо для значений параметра, принадлежащих заранее оговоренному множеству. Этот тип задач является базовым при овладении темой «Задачи с параметрами», поскольку вложенный труд предопределяет успех и при решении задач всех других основных типов.

11 Тип 2. Уравнения, неравенства, их системы, для которых требуется определить количество решений в зависимости от значения параметра (параметров). При решении задач данного типа нет необходимости ни решать заданные уравнения, неравенства, их системы, ни приводить эти решения; такая лишняя в большинстве случаев работа является тактической ошибкой, приводящей к неоправданным затратам времени. Но иногда прямое решение является единственным разумным путем получения ответа при решении задачи типа 2.

12 Тип 3. Уравнения, неравенства, их системы, для которых требуется найти все те значения параметра, при которых указанные уравнения, неравенства, их системы имеют заданное число решений (в частности, не имеют или имеют бесконечное множество решений). Задачи типа 3 в каком-то смысле обратны задачам типа 2.

13 Тип 4. Уравнения, неравенства, их системы и совокупности, для которых при искомых значениях параметра множество решений удовлетворяет заданным условиям в области определения. Например, найти значения параметра, при которых: 1) уравнение выполняется для любого значения переменной из заданного промежутка; 2) множество решений первого уравнения является подмножеством множества решений второго уравнения и т. д.

14 Основные способы (методы) решения задач с параметром. Способ I (аналитический). Аналитический способ решения задач с параметром есть самый трудный способ, требующий высокой грамотности и наибольших усилий по овладению им. Способ II (графический). В зависимости от задачи (с переменной x и параметром a) рассматриваются графики или в координатной плоскости Оху, или в координатной плоскости Оха. Способ III (решение относительно параметра). При решении этим способом переменные x и a принимаются равноправными и выбирается та переменная, относительно которой аналитическое решение признается более простым. После естественных упрощений возвращаемся к исходному смыслу переменных x и a и заканчиваем решение.

15 Пример 1. Найти значения параметра а, при которых уравнение а(2а + 3)х + а 2 = а 2 х + 3а имеет единственный отрицательный корень. Решение. Данное уравнение равносильно следующему:. Если а(а + 3) 0, то есть а 0, а –3, то уравнение имеет единственный корень х =. х

16 Пример 2. Решите уравнение. Решение. Так как знаменатель дроби не может равняться нулю, имеем (b – 1)(x + 3) 0, то есть b 1, x –3. Умножив обе части уравнения на (b – 1)(x + 3) 0, получаем уравнение: Это уравнение является линейным относительно переменной х. При 4b – 9 = 0, то есть b = 2,25 уравнение принимает вид: При 4b – 9 0, то есть b 2,25 корень уравнения x =. Теперь надо проверить, нет ли таких значений b, при которых найденное значение х равно –3. Таким образом, при b 1, b 2,25, b –0,4 уравнение имеет единственный корень x =. О т в е т: при b 1, b 2,25, b –0,4 корень x = при b = 2,25, b = –0,4 решений нет; при b = 1 уравнение не имеет смысла.

17 Типы задач 2 и 3 отличает то, что при их решении не требуется получить явное решение, а нужно лишь найти те значения параметра, при которых это решение удовлетворяет тем или иным условиям. Примерами таких условий для решения могут служить следующие : существует решение; не существует решения; существует единственное решение; существует положительное решение; существует ровно k решений; существует решение, принадлежащее указанному промежутку. В этих случаях оказывается очень полезен графический способ решения задач с параметрами.

18 Можно выделить две разновидности применения графического метода при решении уравнения f (х) = f (а): На плоскости Оху рассматриваются график у = f (х) и семейство графиков у = f (а). Сюда же относятся задачи, решаемые с помощью «пучка прямых». Этот способ оказывается удобен в задачах с двумя неизвестными и одним параметром. На плоскости Оха (которую называют также фазовой) рассматриваются графики, в которых х – аргумент, а а – значение функции. Этот способ обычно применяется в задачах, в которых фигурируют лишь одна неизвестная и один параметр (или сводящиеся к таким).

19 Пример 1. При каких значениях параметра а уравнение 3х 4 + 4х 3 – 12х 2 = а имеет не менее трех корней? Решение. Построим графики функций f (х) = 3х 4 + 4х 3 – 12х 2 и f (х) = а в одной системе координат. Имеем: f ‘(х) = 12х х 2 – 24х = 12х(х + 2)(х – 1), f ‘(х) = 0 при х = –2 (точка минимума), при х = 0 (точка максимума) и при х = 1 (точка максимума). Найдем значения функции в точках экстремума: f (–2) = –32, f (0) = 0, f (1) = –5. Строим схематически график функции с учетом точек экстремума. Графическая модель позволяет ответить на поставленный вопрос: уравнение 3х 4 + 4х 3 – 12х 2 = а имеет не менее трех корней, если –5

20 Пример 2. Сколько корней при различных значениях параметра а имеет уравнение ? Решение. Ответ на поставленный вопрос связан с числом точек пересечения графика полуокружности у = и прямой у = х + а. Прямая, являющаяся касательной, имеет формулу у = х +. Заданное уравнение не имеет корней при а ; имеет один корень при –2

21 Пример3. Сколько решений имеет уравнение |х + 2| = ах + 1 в зависимости от параметра а? Решение. Можно построить графики у = |х + 2| и у = ах + 1. Но мы поступим иначе. При х = 0 (21) решений нет. Разделим уравнение на х: и рассмотрим два случая:1)х > –2 или х=2 2)2) х –2 или х=2 2)2) х

22 Пример использования «пучка прямых» на плоскости. Найдите значения параметра a, при которых уравнение |3x + 3| = ax + 5 имеет единственное решение. Решение. Уравнение |3x + 3| = ax + 5 равносильно следующей системе: Уравнение y – 5 = a(x – 0) задает на плоскости пучок прямых с центром A (0; 5). Проведем прямые из пучка прямых, которые будут параллельны сторонам уголка, являющегося графиком y = |3x + 3|. Эти прямые l и l 1 пересекают в одной точке график y = |3x + 3|. Уравнения этих прямых y = 3x + 5 и у = –3х + 5. Кроме того, всякая прямая из пучка, расположенная между этими прямыми, также будет пересекать график y = |3x + 3| в одной точке. Значит, искомые значения параметра [–3; 3].

23 Алгоритм решения уравнений с использованием фазовой плоскости: 1. Находим область определения уравнения. 2. Выражаем параметр а как функцию от х. 3. В системе координат хОа строим график функции а = f(х) для тех значений х, которые входят в область определения данного уравнения. 4. Находим точки пересечения прямой а = с, где с є (-; +) с графиком функции а = f(х). Если прямая а = с пересекает график а = f(х), то определяем абсциссы точек пересечения. Для этого достаточно решить уравнение а = f(х) относительно х. 5.Записываем ответ.

24 Пример решения неравенства с помощью «фазовой плоскости». Решите неравенство х. Решение.По равносильному переходу Теперь на плоскости Оха построим графики функций Точки пересечения параболы и прямой х 2 – 2х = –2х х = 0. Условие а –2х автоматически выполняется при а х 2 – 2х Таким образом, в левой полуплоскости (х

Презентация «Решение уравнений и неравенств с параметрами»

Презентация разработана к проекту «Решение уравнений и неравенств с параметрами». Способствует лучшему усвоению темы.

Просмотр содержимого документа
«Презентация «Решение уравнений и неравенств с параметрами»»

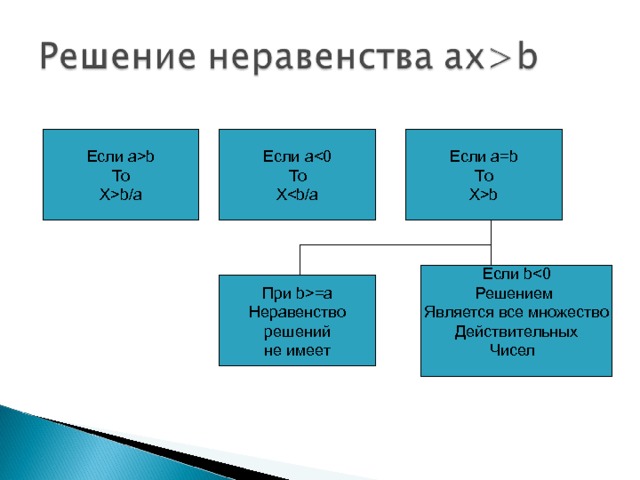
а 1 /а 2 = b 1 /b 2 = с 1 /с 2 ,

Если а 1 /а 2 не равно

b 1 /b 2 , то решение –

а 1 /а 2 = b 1 /b 2 ,

Но не равно с 1 /с 2 ,

При a=0 уравнение не имеет смысла

При a+1=0, a=-1 уравнение принимает вид 0 x=2, не имеет решения

При a≠0, a≠-1 уравнение имеет единственный корень x=2a/(a+1)

Ответ: при a=0 уравнение не имеет смысла, при а=-1 решений нет, при а≠0, а≠-1 х=2а/(а+1)

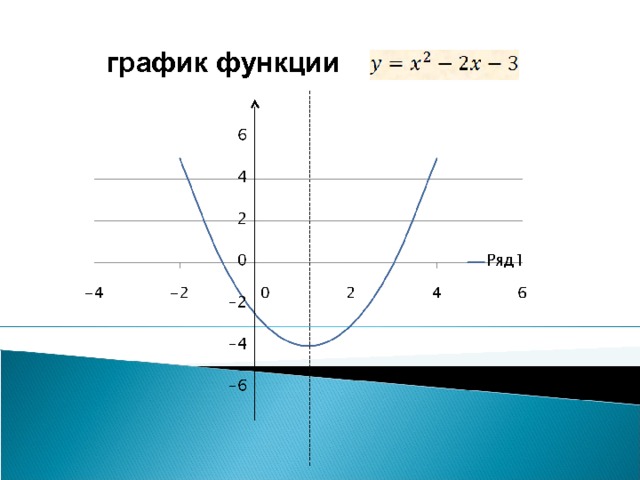
При каких значениях параметра а уравнение

имеет ровно 3 корня .

Построение графика функции

Построим график функции , и при значениях y

1. Общая характеристика функции

2.Координаты вершины (1;4)

3.Точки пересечения с осью ох: y =0

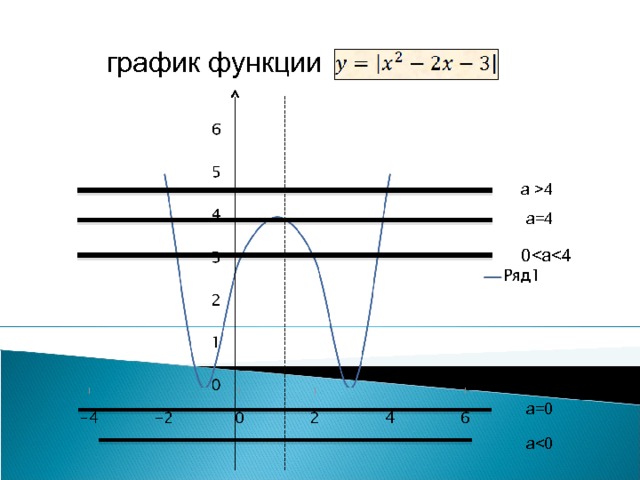
4 а=4 0 a=0 a» width=»640″

a 4 — два решения При 0 При а=4 три решения (x=1+2 , x=1-2 , x = 1 ) » width=»640″

При a=0 (x=-1,x=3 ) и при а 4 — два решения

При а=4 три решения

b Если ab То Xb/a Если aТо XЕсли bРешением Является все множество Действительных Чисел При b=a Неравенство решений не имеет » width=»640″

Является все множество

• Находим область определения данного неравенства.
• Сводим неравенство к уравнению.
• Выражаем а как функцию от х.
• В системе координат хОа строим графики функций а =  (х) для тех значений х, которые входят в область определения данного неравенства.
• Находим множества точек, удовлетворяющих данному неравенству.
• Исследуем влияние параметра на результат.
• найдём абсциссы точек пересечения графиков.
• зададим прямую а=соnst и будем сдвигать её от —  до+ 
• Записываем ответ.

2(x-1) Решение : x-2x-2-1 (m-2)x-3 Данное неравенство является линейным, поэтому контрольным значением для него будет m-2=0 Далее имеем : При m-20. то есть m2 , x-3/(m-2) , x3/(2-m) При m-2При m=2 неравенство принимает вид 0 x-3. Здесь x- любое действительное число. Ответ: при m2 x3/(2-m); при mпри m=2 x- любое действительное число » width=»640″

Решить относительно x неравенство :

Данное неравенство является линейным, поэтому контрольным значением для него будет m-2=0

При m-20. то есть m2 , x-3/(m-2) , x3/(2-m)

При m=2 неравенство принимает вид 0 x-3. Здесь

x- любое действительное число.

Ответ: при m2 x3/(2-m); при m

при m=2 x- любое действительное число

• Далингер В. А. “Геометрия помогает алгебре”. Издательство “Школа — Пресс”. Москва 1996 г.
• Далингер В. А. “Все для обеспечения успеха на выпускных и вступительных экзаменах по математике”. Издательство Омского педуниверситета. Омск 1995 г.
• Окунев А. А. “Графическое решение уравнений с параметрами”. Издательство “Школа — Пресс”. Москва 1986 г.
• Письменский Д. Т. “Математика для старшеклассников”. Издательство “Айрис”. Москва 1996 г.
• Ястрибинецкий Г. А. “Уравнений и неравенства, содержащие параметры”. Издательство “Просвещение”. Москва 1972 г.
• Г. Корн и Т.Корн “Справочник по математике”. Издательство “Наука” физико–математическая литература. Москва 1977 г.
• Амелькин В. В. и Рабцевич В. Л. “Задачи с параметрами” .
• www.bymath.net/studyguide/alg/sec/alg31.html
• www.math4you.ru/theory/TerVerMatStat/TerVerKom/
• www.pm298.ru›