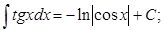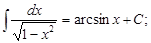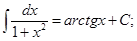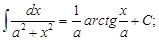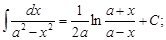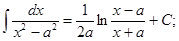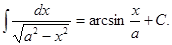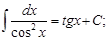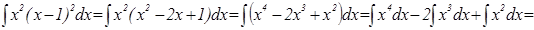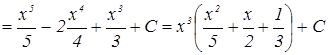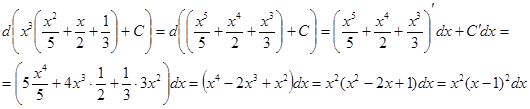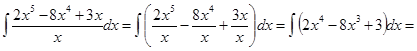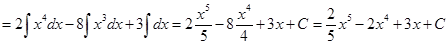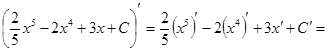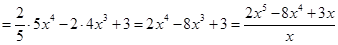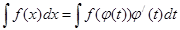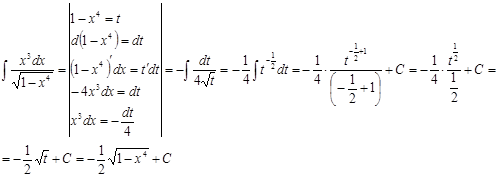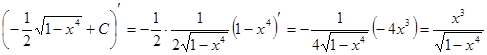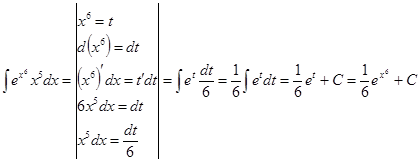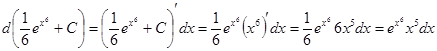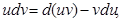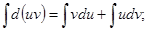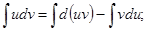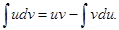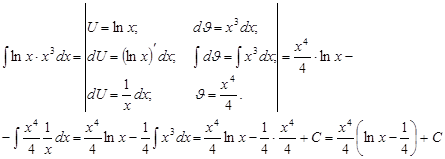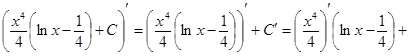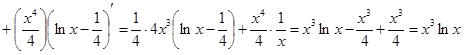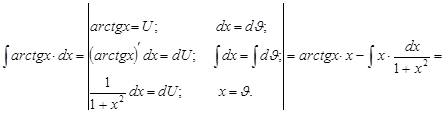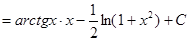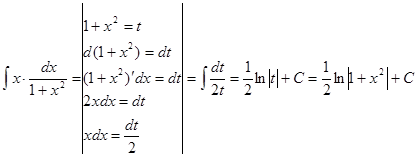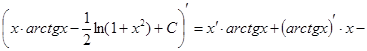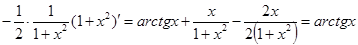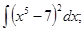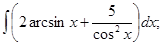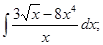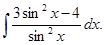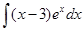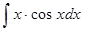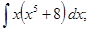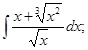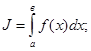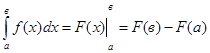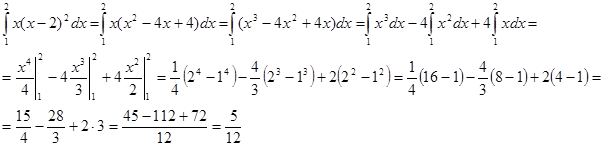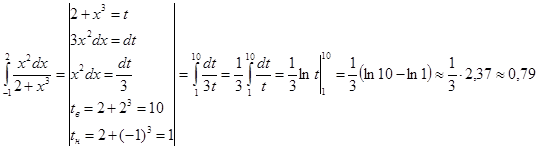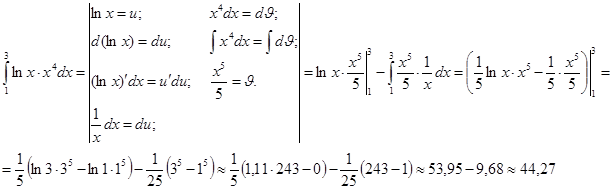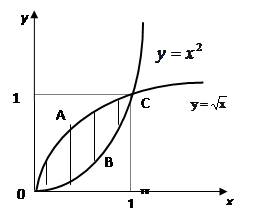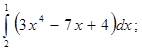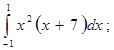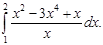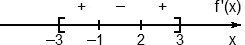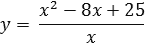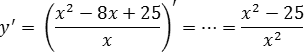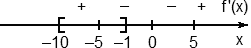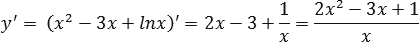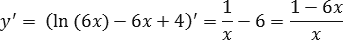Экстремумы функции
Необходимое условие экстремума функции одной переменной
Достаточное условие экстремума функции одной переменной
Если в точке x * выполняется условие:
Пример №1 . Найти наибольшее и наименьшее значения функции: 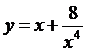
Решение.
Критическая точка одна x1 = 2 (f’(x)=0). Эта точка принадлежит отрезку [1;3]. (Точка x=0 не является критической, так как 0∉[1;3]).
Вычисляем значения функции на концах отрезка и в критической точке.
f(1)=9, f(2)= 5 /2, f(3)=3 8 /81
Ответ: fmin= 5 /2 при x=2; fmax=9 при x=1
Пример №2 . С помощью производных высших порядков найти экстремум функции y=x-2sin(x) .
Решение.
Находим производную функции: y’=1-2cos(x) . Найдем критические точки: 1-cos(x)=2, cos(x)=½, x=± π /3+2πk, k∈Z. Находим y’’=2sin(x), вычисляем 

Пример №3 . Исследовать на экстремум фцнкцию в окрестностях точки x=0.
Решение. Здесь необходимо найти экстремумы функции. Если экстремум x=0 , то выяснить его тип (минимум или максимум). Если среди найденных точек нет x = 0, то вычислить значение функции f(x=0).
Следует обратить внимание, что когда производная с каждой стороны от данной точки не меняет своего знака, не исчерпываются возможные ситуации даже для дифференцируемых функций: может случиться, что для сколь угодно малой окрестности по одну из сторон от точки x0 или по обе стороны производная меняет знак. В этих точках приходится применять другие методы для исследования функций на экстремум.
Пример №4 . Разбить число 49 на два слагаемых, произведение которых будет наибольшим.
Решение. Обозначим x — первое слагаемое. Тогда (49-x) — второе слагаемое.
Произведение будет максимальным: x·(49-x) → max
или
49x — x 2
экстремум с помощью производной второго порядка
экстремума дифференцируемой функции
Теорема: Если функция 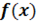
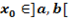
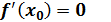
Теорема: Если производная 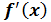
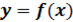
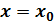
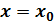
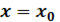
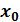
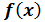
Правило исследования дифференцируемой функции на
экстремумы с помощью первой производной
Рассмотрим данное правило на примере:
1. Находят производную функции: 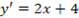
2.Находят критическое значение аргумента, для чего 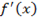
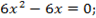 | |
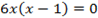 | |
 | — критические точки |
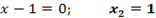 |
3. Критические значения аргумента располагают в возрастающем порядке. Определяют знаки производной для значений аргументов, расположенных правее и левее и близких к критическим точкам. Если знак производной меняется с (-) на (+), то данное значение аргумента является точкой минимума, если знак производной меняется с (+) на (-), то данное значение аргумента является точкой максимума.
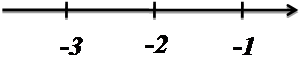 |
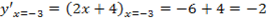 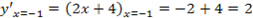 |
Знак производной изменился при переходе через критическую точку с (-) на (+), значит точка 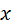
4. Вычисляют значение функции в точках максимума и минимума: Ymax, Ymin.
Данное правило исследования функции на экстремумы можно представить в виде следующей таблицы:
| Критическое значение аргумента | Знаки производной 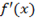 , при переходе через критическую точку х=х0 , при переходе через критическую точку х=х0 | Характер критической точки | 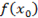 | |
| х0 | x х0 | |||
| x1 x2 x3 x4 | — + — + | + — — + | Min Max Нет экстремума Нет экстремума | 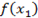 min min 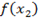 max max |
Правило исследования дифференцируемой функции на
экстремум с помощью производной второго порядка
Если при данном критическом значении аргумента вторая производная окажется отрицательной, то при этом значении аргумента функция имеет максимум. Если вторая производная окажется положительной, то при этом значении аргумента функция имеет минимум.
Если при данном критическом значении вторая производная обращается в 0 или в бесконечно большую величину, то исследование функции на экстремум ведется с помощью первой производной.
Например:
1. Находим первую производную:
2. Находим критические точки:
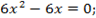 | |
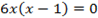 | |
 | — критические точки |
 |
3. Находим вторую производную: 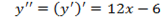
4. Во вторую производную подставляем критические точки:
3. ВЫПУКЛОСТЬ И ВОГНУТОСТЬ ФУНКЦИИ. ТОЧКИ ПЕРЕГИБА
Кривая 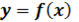
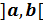

Кривая 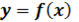
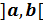

Точка на непрерывной кривой, отделяющая участок выпуклости от участка вогнутости, называется точкой перегиба.
Исследовать функцию на выпуклость и вогнутость: 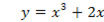
Находим
Кривая выпукла ,если
Т. о. кривая выпукла в интервале
Кривая вогнута , если
Таким образом, кривая вогнута в интервале 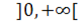
Эталоны решения типовых задач
Задача №1. Построить график функции у=х 3 -3х.
При построении графиков функций удобно действовать по следующей схеме:
1. найти область определения функции;
2. установить, обладает ли функция симметрий (исследовать функцию на четность);
3. исследовать функцию на непрерывность, периодичность;
4. рассмотреть поведение функции в окрестностях точек разрыва;
5. определить поведение функции в бесконечности;
6. найти точки пересечения графика функции с осями координат, если это возможно ( хотя бы приближенно);
7. найти интервалы возрастания, убывания и точки экстремума функции;
8. определить точки перегиба;
9. определить интервалы выпуклости и вогнутности;
10. составить сводную таблицу и построить график.
В ходе построения графика по мере необходимости можно получить допольнительно ряд значений функции при некоторых частных значениях аргумента х, т.е. еще ряд точек графика. Разумеется, в процессе исследования функции не обязательно строго придерживаться приведенной схемы, иногда даже удобно изменить порядок действий.
1. Функция определена при всех
2. На концах интервала lim (x 3 -3x)=-¥; lim (x 3 -3x)=+¥,
3. Определим интервалы возрастания и убывания функции. Функция возрастает на интервале, если f ¢ (x)>0. В данном случае f ¢ (x)=3х 2 -3>0, если х 2 >1 или |х|>1. Следовательно, функция у=х 2 -3х возрастает на интервалах 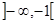
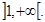
4. Определим критические точки и исследуем их характер. Из условия 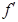
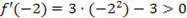
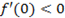
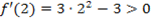
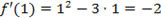
5. Определим точку перегиба: 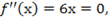
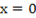
6.Определим интервалы выпуклости и вогнутности. Кривая выпукла при условии 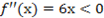
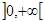
7. Найдем точки пересечения кривой с осью Ох.Из системы уравнений 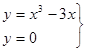
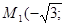
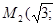
8. Сведем результаты исследования в таблицу:
| х | -1 |  | 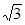 |
| f(x) | -2 | ||
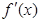 | -3 | ||
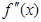 | -6 | ||
| Характер точки | Максимум | Перегиб | Минимум |
9. Строим график функции у=х 3 -3х
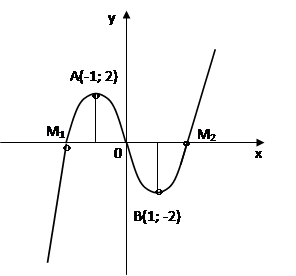 |
Рис 4. График функции у=х 3 -3х.
Задача 2. Установить, при каком процентом содержании у кислорода в газовой смеси скорость окисления азота будет максимальной, если уравнение кинетики имеет вид 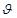
Решение. Найдем производную функции 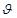
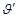
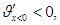
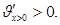
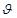
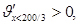
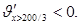
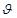
Задача 2 . Реакция организма на введенный лекарственный препарат может выражаться в понижении температуры, повышении давления и т.д. Степень реакции зависит от назначенной дозы лекарства. Пусть х обозначает дозу назначенного лекарственного препарата, а степень реакции описывается функцией у=f(x)=x 2 (a-x), где а-положительная постоянная. При каком значении х реакция максимальна?
Решение. Найдем производную функции и приравняем ее к нулю: 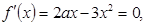
Значение х1=0 указывает на то, что в организм лекарство не вводилось. Исследуем точку х2=2а/3: 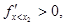
Задачи для домашнего решения
1. Построить графики функций:
а) 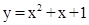
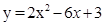
б) 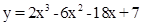
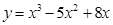
в) 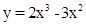
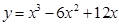
2. Известно, что если полимерные молекулы образуются путем рекомбинации, то мольная доля у молекулы полимера с числом звеньев х имеет вид 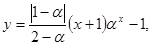
3. При построении математической модели хлорирования органических соединений получают следующую функциональную зависимость между концентрацией у монохлорзамещенных продуктов и концентрацией х нехлорированного сырья: 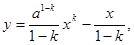
Задачи для решения на практических занятиях:
- Построить графики функций.
а) у=х(2-х) 2 ; г)у=х 3 —
б) у=4х- 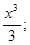
в) у=2х 2 —
- Растворение лекарственных веществ из таблеток подчиняется уравнению: с=с0е — kt , где с0-исходное количество лекарственного вещества в таблетке, с-количество лекарственного вещества в таблетке, оставшегося ко времени растворения t, k-постоянная скорости растворения. Построить график функции с(t) для t³0.
- В питательную среду вносят 1000 бактерий. Численность у бактерий возрастает согласно уравнению у=1000+1000t/(100+t 2 ),где t-время, (в часах). Определить максимальное количество бактерий.
- Реакция организма на два лекарственных препарата выражается соответственно функциями
и
. Определить максимальные реакции на оба препарата и сравнить их.
Интегральное исчисление является составной частью математического анализа и применяется при решении многих задач химии, биологии именно в тех случаях, когда по известной производной требуется найти вид самой функции.
1. Научиться находить интегралы методом непосредственного интегрирования.
2. Научиться находить интегралы методом подстановки.
3. Научиться находить интегралы методом интегрирования по частям.
1. ПЕРВООБРАЗНАЯ ФУНКЦИЯ И НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
Процесс дифференцирования, т.е. нахождение производной или дифференциала функции, с физической точки зрения сводится к следующему: зная закон движения материальной системы, определить мгновенное значение скорости в данной точке траектории её движения. С геометрической точки зрения, этот процесс состоит в нахождении tga угла наклона касательной, проведённой к графику функции в данной точке.
Но часто ставится и обратная задача, т. е. необходимо определить закон движения материальной системы, зная её скорость, или по tga угла наклона касательной найти соответствующую функцию. Для решения этой задачи вводится понятие неопределённого интеграла, а сам процесс решения называется интегрированием.
Другими словами: если процесс дифференцирования состоит в нахождении производной данной функции, то процесс интегрирования — это нахождение функции по её производной или дифференциалу.
Найти интеграл значит найти первообразную функции F(х) и сложить её с произвольной постоянной интегрирования С:
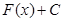
Таким образом, каждый неопределенный интеграл имеет бесчисленное множество решений или семейство первообразных.
Функция F(x), имеющая функцию f(x) своей производной или f(x)dx своим дифференциалом, называется первообразной данной функции:
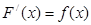
Неопределенный интеграл в общем виде записывается:
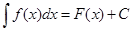
где ∫-знак неопределённого интеграла,
f(x) — подинтегральная функция,
f(x)dx — подинтегральное выражение,
F(x) – первообразная функция
С – произвольная постоянная интегрирования
F(x)+С–решение неопределенного интеграла или семейство первообразных.
2. СВОЙСТВА НЕОПРЕДЕЛЁННОГО ИНТЕГРАЛА
1. Производная от неопределённого интеграла равна подинтегральной функции:
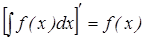
2. Дифференциал от неопределённого интеграла равен подинтегральному выражению:
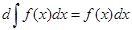
3. Интеграл от дифференциала первообразной функции равен самой первообразной, сложенной с произвольной постоянной:
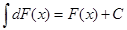
4. Постоянный множитель можно вынести за знак интеграла:
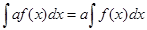
5. Интеграл алгебраической суммы функций равен алгебраической сумме интегралов этих функций:
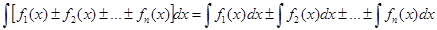
3. ТАБЛИЦА ОСНОВНЫХ ИНТЕГРАЛОВ
1. 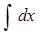
2. 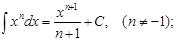
3. 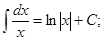
4. 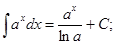
5. 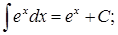
6. 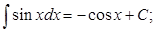
7. 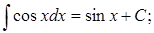
8. 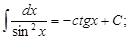
9.
4. ПРОСТЕЙШИЕ МЕТОДЫ ИНТЕГРИРОВАНИЯ
1. Метод непосредственного интегрирования
Метод непосредственного интегрирования основан на преобразовании подинтегральной функции, применении свойств неопределённого интеграла и приведении подинтегрального выражения к табличной форме.
1)
Проверка(на основании свойства №2 неопределённого интеграла):
2)
Проверка(на основании свойства №1 неопределённого интеграла):
2. Метод подстановки (замены переменной)
Этот метод основан на введении новой переменной. В интеграле 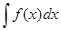
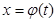
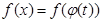
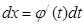
1)
Проверка:
2)
Проверка(на основании свойства №2 неопределённого интеграла):
3. Интегрироване по частям
Пусть u иv — дифференцируемые функции. Раскроем дифференциал произведения этих функций:
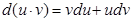
откуда
Проинтегрируем полученное выражение:
Проверка(на основании свойства №1 неопределённого интеграла):
2)
Решаем
Проверка(на основании свойства №1 неопределённого интеграла):
Задачи для домашнего решения
I. Метод непосредственного интегрирования
а) 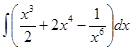
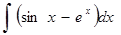
б) 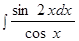
в) 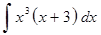
г) 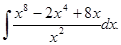
д) 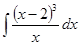
II. Метод подстановки (замены переменной)
а) 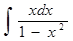
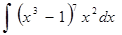
б) 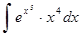
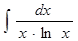
в) 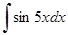
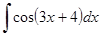
г) 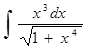
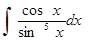
д) 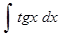
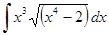
III. Метод интегрирования по частям
а) 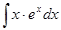
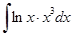
б) 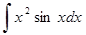
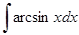
Задачи для решения на практических занятиях:
I. Метод непосредственного интегрирования
а) 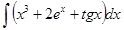
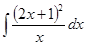
б) 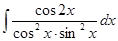
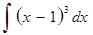
в) 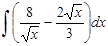
г) 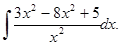
д) 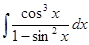
е) 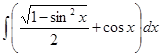
II. Метод подстановки (замены переменной)
а) 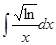
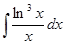
б) 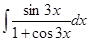
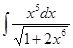
в) 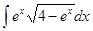
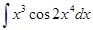
г) 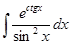
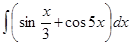
д) 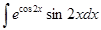
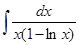
е) 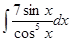
III. Метод интегрирования по частям
а) 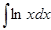
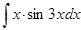
б) 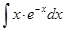
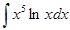
в) 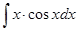
г) 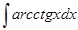
При математических расчётах часто требуется найти приращение первообразной функции при изменении её аргумента в заданных пределах. Такую задачу приходится решать при вычислении площадей и объёмов различных фигур, при определении среднего значения функции, при вычислении работы переменной силы. Эти задачи могут быть решены вычислением соответствующих определённых интегралов.
1. Научиться вычислять определённый интеграл с помощью формулы Ньютона-Лейбница.
2. Уметь применять понятие определённого интеграла для решения прикладных задач.
1. ПОНЯТИЕ ОПРЕДЕЛЁННОГО ИНТЕГРАЛА И ЕГО ГЕОМЕТРИЧЕСКИЙ СМЫСЛ
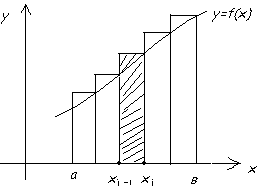
Рассмотрим задачу о нахождении площади криволинейной трапеции.
Пусть дана некоторая функция y=f(x), график которой изображён на рисунке.
Рис 1. Геометрический смысл определенного интеграла.
На оси 0х выберем точки “a”и “в” и восстановим из них перпендикуляры до пересечения с кривой. Фигура ограниченная кривой, перпендикулярами и осью 0х называется криволинейной трапецией. Разобьём интервал 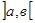
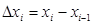
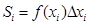
Тогда площадь всех достроенных прямоугольников в интервале 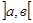
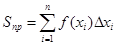
Если каждый из отрезков достаточно мал и стремится к нулю, то суммарная площадь прямоугольников будет стремиться к площади криволинейной трапеции:
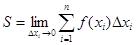
Итак, задача о вычислении площади криволинейной трапеции сводится к определению предела суммы.
Интегральная сумма есть сумма произведений приращения аргумента на значение функции f(x), взятой в некоторой точке интервала, в границах которого изменяется аргумент. Математически задача о нахождении предела интегральной суммы, если приращение независимой переменной стремится к нулю, приводит к понятию определённого интеграла.
Функция f(x) в некотором интервале от х=адо х=в интегрируема, если существует такое число, к которому стремится интегральная сумма при Dх®0. В этом случае число J называют определённым интегралом функции f(x) в интервале 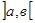
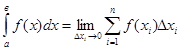
где ]а, в[ – область интегрирования,
а–нижний предел интегрирования,
в–верхний предел интегрирования.
Таким образом, с точки зрения геометрии, определённый интеграл есть площадь фигуры, ограниченной графиком функции в определённом интервале ]а, в[ и осью абцисс.
2. СВЯЗЬ МЕЖДУ ОПРЕДЕЛЁННЫМ И НЕОПРЕДЕЛЁННЫМ ИНТЕГРАЛАМИ. ФОРМУЛА НЬЮТОНА-ЛЕЙБНИЦА
Неопределённый интеграл — это совокупность первообразных функций. Определённый интеграл — это число. Связь между ними задаётся формулой Ньютона-Лейбница.
Теорема. Значение определённого интеграла равно разности значений любой первообразной от подинтегральной функции, взятой при верхнем и нижнем пределами интегрирования:
Например: 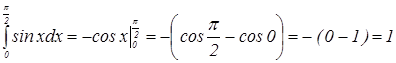
3. СВОЙСТВА ОПРЕДЕЛЁННОГО ИНТЕГРАЛА
1. Определённый интеграл не зависит от обозначения переменной интегрирования:
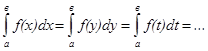
2. Определённый интеграл от алгебраической суммы конечного числа непрерывных функций 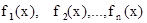
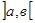
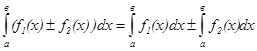
3. Постоянный множитель можно вынести за знак интеграла:
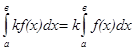
4. Если верхний и нижний пределы интегрирования поменять местами, то определённый интеграл изменит свой знак на противоположный:
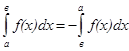
5. Если а=в, то 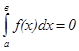
6. Если отрезок интегрирования 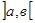
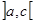
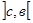
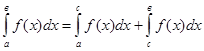
7. Если подинтегральная функция на отрезке интегрирования сохраняет постоянный знак, то интеграл представляет собой число того же знака, что и функция, т.е. если 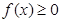
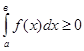
8. Значение определённого интеграла заключено между произведениями наибольшего и наименьшего значений подинтегральной функции на длину интервала интегрирования:
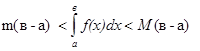
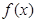
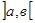
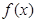
9. Определённый интеграл от непрерывной функции равен произведению значения этой функции в некоторой промежуточной точке х=С отрезка интегрирования 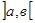
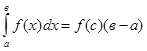
где f(c) — среднее значение функции в интервале.
4. ОСНОВНЫЕ МЕТОДЫ НАХОЖДЕНИЯ ОПРЕДЕЛЁННОГО ИНТЕГРАЛА
1. Метод непосредственного интегрирования
2. Метод подстановки
Примечание: При вычислении интеграла методом постановки переходим к новым пределам интегрирования для переменной t.
Метод интегрирования по частям
Вычисление площадей фигур, ограниченных линиями, уравнения которых заданы
Например: Вычислить площадь фигуры, ограниченную линиями:
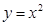
Решение: Представим искомую площадь графически.
Искомая площадь площадь фигуры ОАСВ – заштрихована.
Находим точки пересечения линий: 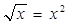
В соответствии с геометрической интерпретацией определённого интеграла, определённый интеграл функции 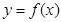
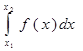
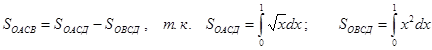
Искомая площадь: 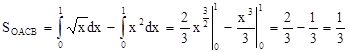
Ответ: Искомая площадь равна 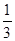
Задачи для домашнего решения
I. Метод непосредственного интегрирования
а) 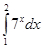
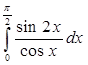
б) 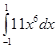
в); 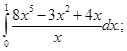
г) 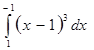
II. Метод подстановки (замены переменной)
а) 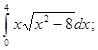
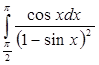
б) 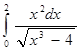
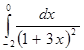
в) 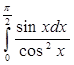
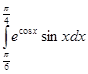
г) 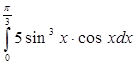
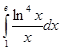
III. Метод интегрирования по частям
а) 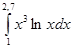
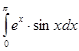
б) 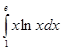
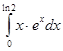
Найти площадь фигуры, ограниченную линиями:
а) 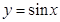
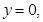
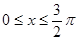
б) 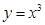
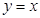
в) 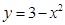
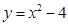
г) 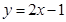
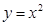
Задачи для решения на практических занятиях:
а) 

б) 
в); 
Задача B15 — исследование функции с помощью производной
В задаче B15 предлагается исследовать на экстремумы функцию, заданную формулой. Это стандартная задача по математическому анализу, и ее сложность сильно меняется зависимости от рассматриваемой функции: некоторые из них решаются буквально устно, другие же требуют серьезных размышлений.
Прежде чем изучать методы решения, надо усвоить некоторые термины из области математического анализа. Итак, в задаче B15 требуется найти с помощью производной следующие величины:
- (минимума) — значение переменной, при которой функция достигает своей наибольшей (наименьшей) величины. Такие точки еще называются точками экстремума.
- (минимум) функции — наибольшее (наименьшее) значение функции при указанных ограничениях. Другое название — глобальные экстремумы.
При этом глобальные экстремумы обычно ищутся не на всей области определения функции, а лишь на некотором отрезке [a; b]. Важно понимать, что глобальный экстремум и значение функции в точке экстремума далеко не всегда совпадают. Поясним это на конкретном примере:
Задача. Найти точку минимума и минимальное значение функции y = 2x 3 − 3x 2 − 12x + 1 на отрезке [−3; 3].
Сначала найдем точку минимума, для чего вычислим производную:
y’ = (2x 3 − 3x 2 − 12x + 1)’ = 6x 2 − 6x − 12.
Найдем критические точки, решив уравнение y’ = 0. Получим стандартное квадратное уравнение:
y’ = 0 ⇒ 6x 2 − 6x − 12 = 0 ⇒ . ⇒ x1 = −1, x2 = 2.
Отметим эти точки на координатной прямой, добавим знаки производной и ограничения — концы отрезка:
Масштаб картинки не имеет значения. Самое главное — отметить точки в правильной последовательности. Из школьного курса математики известно, что в точке минимума производная меняет знак с минуса на плюс. Отсчет всегда идет слева направо — в направлении положительной полуоси. Поэтому точка минимума одна: x = 2.
Теперь найдем минимальное значение функции на отрезке [−3; 3]. Оно достигается либо в точке минимума (тогда она становится точкой глобального минимума), либо на конце отрезка. Заметим, что на интервале (2; 3) производная всюду положительна, а значит y(3) > y(2), поэтому правый конец отрезка можно не рассматривать. Остались лишь точки x = −3 (левый конец отрезка) и x = 2 (точка минимума). Имеем:
y(−3) = 2(−3) 3 − 3(−3) 2 − 12(−3) + 1 = −44;
y(2) = 2*2 3 − 3*2 2 − 12*2 + 1 = −19.
Итак, наименьшее значение функции достигается на конце отрезка и равно −44.
Из приведенных рассуждений следует важный факт, о котором многие забывают. Функция принимает максимальное (минимальное) значение не обязательно в точке экстремума. Иногда такое значение достигается на конце отрезка, и производная там не обязана равняться нулю.
Схема решения задач B15
Если в задаче B15 требуется найти максимальное или минимальное значение функции f(x) на отрезке [a; b], выполняем следующие действия:
- Найти производную функции: f’(x).
- Решить уравнение f’(x) = 0. Если корней нет, пропускаем третий шаг и переходим сразу к четвертому.
- Из полученного набора корней вычеркнуть все, что лежит за пределами отрезка [a; b]. Оставшиеся числа обозначим x1, x2, . xn — их, как правило, будет немного.
- Подставим концы отрезка [a; b] и точки x1, x2, . xn в исходную функцию. Получим набор чисел f(a), f(b), f(x1), f(x2), . f(xn), из которого выбираем наибольше или наименьшее значение — это и будет ответ.
Небольшое пояснение по поводу вычеркивания корней, когда они совпадают с концами отрезка. Их тоже можно вычеркнуть, поскольку на четвертом шаге концы отрезка все равно подставляются в функцию — даже если уравнение f’(x) = 0 не имело решений.
Также следует внимательно читать условие задачи. Когда требуется найти значение функции (максимальное или минимальное), концы отрезка и точки x1, x2, . xn подставляются именно в функцию, а не в ее производную.
Задача. Найти наибольшее значение функции y = x 3 + 3x 2 − 9x − 7 на отрезке [−5; 0].
Для начала найдем производную: y’ = (x 3 + 3x 2 − 9x − 7)’ = 3x 2 + 6x − 9.
Затем решаем уравнение: y’ = 0 ⇒ 3x 2 + 6x − 9 = 0 ⇒ . ⇒ x = −3; x = 1.
Вычеркиваем корень x = 1, потому что он не принадлежит отрезку [−5; 0].
Осталось вычислить значение функции на концах отрезка и в точке x = −3:
y(−5) = (−5) 3 + 4·(−5) 2 − 9·(−5) − 7 = −12;
y(−3) = (−3) 3 + 4·(−3) 2 − 9·(−3) − 7 = 20;
y(0) = 0 3 + 4·0 2 − 9·0 − 7 = −7.
Очевидно, наибольшее значение равно 20 — оно достигается в точке x = −3.
Теперь рассмотрим случай, когда требуется найти точку максимума или минимума функции f(x) на отрезке [a; b]. Если отрезок не задан, функция рассматривается на своей области определения. В любом случае, схема решения такова:
- Найти производную функции: f’(x).
- Решить уравнение f’(x) = 0. Если производная — дробно-рациональная функция, дополнительно выясняем, когда ее знаменатель равен нулю. Полученные корни обозначим x1, x2, . xn.
- Отметить x1, x2, . xn на координатной прямой и расставить знаки, которые принимает производная между этими числами. Если задан отрезок [a; b], отмечаем его и вычеркиваем все, что лежит за его пределами.
- Среди оставшихся точек ищем такую, где знак производной меняется с минуса на плюс (это точка минимума) или с плюса на минус (точка минимума). Такая точка должна быть только одна — это и будет ответ.
Вдумчивый читатель наверняка заметит, что для некоторых функций этот алгоритм не работает. Действительно, существует целый класс функций, для которых нахождение точек экстремума требует более сложных выкладок. Однако такие функции в ЕГЭ по математике не встречаются.
Внимательно отнеситесь к расстановке знаков между точками x1, x2, . xn. Помните: при переходе через корень четной кратности знак у производной не меняется. Когда ищутся точки экстремума, знаки всегда просматриваются слева направо, т.е. по направлению числовой оси.
Задача. Найти точку максимума функции
Поскольку это дробно-рациональная функция, приравниваем к нулю производную и ее знаменатель:
y’ = 0 ⇒ x 2 − 25 = 0 ⇒ . ⇒ x = 5; x = −5;
x 2 = 0 ⇒ x = 0 (корень второй кратности).
Отметим точки x = −5, x = 0 и x = 5 на координатной прямой, расставим знаки и границы:
Очевидно, что внутри отрезка осталась лишь одна точка x = −5, в которой знак производной меняется с плюса на минус. Это и есть точка максимума.
Еще раз поясним, чем отличаются точки экстремума от самих экстремумов. Точки экстремума — это значения переменных, при которых функция принимает наибольшее или наименьшее значение. Экстремумы — это значения самих функций, максимальные или минимальные в некоторой своей окрестности.
Помимо обычных многочленов и дробно-рациональных функций, в задаче B15 встречаются следующие виды выражений:
- Иррациональные функции,
- Тригонометрические функции,
- Показательные функции,
- Логарифмические функции.
С иррациональными функциями проблем, как правило, не возникает. Остальные случаи стоит рассмотреть более подробно.
Тригонометрические функции
Основная сложность тригонометрических функций состоит в том, что при решении уравнений возникает бесконечное множество корней. Например, уравнение sin x = 0 имеет корни x = πn, где n ∈ Z. Ну и как отмечать их на координатной прямой, если таких чисел бесконечно много?
Ответ прост: надо подставлять конкретные значения n. Ведь в задачах B15 с тригонометрическими функциями всегда есть ограничение — отрезок [a; b]. Поэтому для начала берем n = 0, а затем увеличиваем n до тех пор, пока соответствующий корень не «вылетит» за пределы отрезка [a; b]. Аналогично, уменьшая n, очень скоро получим корень, который меньше нижней границы.
Несложно показать, что никаких корней, кроме полученных в рассмотренном процессе, на отрезке [a; b] не существует. Рассмотрим теперь этот процесс на конкретных примерах.
Задача. Найти точку максимума функции y = sin x − 5x·sin x − 5cos x + 1, принадлежащую отрезку [−π/3; π/3].
Вычисляем производную: y’ = (sin x − 5x·sin x − 5cos x + 1)’ = . = cos x − 5x·cos x = (1 − 5x)·cos x.
Затем решаем уравнение: y’ = 0 ⇒ (1 − 5x)·cos x = 0 ⇒ . ⇒ x = 0,2 или x = π/2 + πn, n ∈ Z.
С корнем x = 0,2 все понятно, а вот формула x = π/2 + πn требует дополнительной обработки. Будем подставлять разные значения n, начиная с n = 0.
n = 0 ⇒ x = π/2. Но π/2 > π/3, поэтому корень x = π/2 не входит в исходный отрезок. Кроме того, чем больше n, тем больше x, поэтому нет смысла рассматривать n > 0.
n = −1 ⇒ x = − π/2. Но −π/2 π/4, поэтому корень x = π и значения n > 1 надо вычеркнуть.
n = −1 ⇒ x = −π. Но π 1. Поэтому корней нет.
Если корней нет, то и вычеркивать ничего не надо. Переходим к последнему шагу — вычисляем значение функции:
y(−3π/2) = 7sin (−3π/2) − 8·(−3π/2) + 5 = . = 12π + 12;
y(0) = 7sin 0 − 8·0 + 5 = 5.
Поскольку число 12π + 12 в бланк ответов не записать, остается лишь y = 5.
Показательные функции
Вообще говоря, показательная функция — это выражение вида y = a x , где a > 0. Но в задаче B15 встречаются только функции вида y = e x и, в крайнем случае, y = e kx + b . Причина в том, что производные этих функций считаются очень легко:
- (e x )» = e x . Ничего не изменилось.
- (e kx + b)» = k·e kx + b . Просто добавляется множитель, равный коэффициенту при переменной x. Это частный случай производной сложной функции.
Все остальное абсолютно стандартно. Разумеется, настоящие функции в задачах B15 выглядят более сурово, но схема решения от этого не меняется. Рассмотрим пару примеров, выделяя лишь основные моменты решения — без основательных рассуждений и комментариев.
Задача. Найти наименьшее значение функции y = (x 2 − 5x + 5)e x − 3 на отрезке [−1; 5].
Производная: y’ = ((x 2 − 5x + 5)e x − 3 )’ = . = (x 2 − 3x)e x − 3 = x(x − 3)e x − 3 .
Находим корни: y’ = 0 ⇒ x(x − 3)e x − 3 = 0 ⇒ . ⇒ x = 0; x = 3.
Оба корня лежат на отрезке [−1; 5]. Осталось найти значение функции во всех точках:
y(−1) = ((−1) 2 − 5·(−1) + 5)e − 1 − 3 = . = 11·e −4 ;
y(0) = (0 2 − 5·0 + 5)e 0 − 3 = . = 5·e −3 ;
y(3) = (3 2 − 5·3 + 5)e 3 − 3 = . = −1;
y(5) = (5 2 − 5·5 + 5)e 5 − 3 = . = 5·e 2 .
Из четырех полученных чисел в бланк можно записать лишь y = −1. К тому же, это единственное отрицательное число — оно и будет наименьшим.
Задача. Найти наибольшее значение функции y = (2x − 7)·e 8 − 2x на отрезке [0; 6].
Производная: y’ = ((2x − 7)·e 8 − 2x )’ = . = (16 − 4x)·e 8 − 2x = 4(4 − x)·e 8 − 2x .
Находим корни: y’ = 0 ⇒ 4(4 − x)·e 8 − 2x = 0 ⇒ x = 4.
Корень x = 4 принадлежит отрезку [0; 6]. Ищем значения функции:
y(0) = (2·0 − 7)e 8 − 2·0 = . = −7·e 8 ;
y(4) = (2·4 − 7)e 8 − 2·4 = . = 1;
y(6) = (2·6 − 7)e 8 − 2·6 = . = 5·e −4 .
Очевидно в качестве ответа может выступать лишь y = 1.
Логарифмические функции
По аналогии с показательными функциями, в задаче B15 встречаются только натуральные логарифмы, поскольку их производная легко считается:
- (ln x)’ = 1/x;
- (ln(kx + b))’ = k/(kx + b). В частности, если b = 0, то (ln(kx))’ = 1/x.
Таким образом, производная всегда будет дробно-рациональной функцией. Остается лишь приравнять эту производную и ее знаменатель к нулю, а затем решить полученные уравнения.
Для поиска максимального или минимального значения логарифмической функции помните: натуральный логарифм обращается в «нормальное» число только в точках вида e n . Например, ln 1 = ln e 0 = 0 — это логарифмический ноль, и чаще всего решение сводится именно к нему. В остальных случаях «убрать» знак логарифма невозможно.
Задача. Найти наименьшее значение функции y = x 2 − 3x + ln x на отрезке [0,5; 5].
Находим нули производной и ее знаменателя:
y’ = 0 ⇒ 2x 2 − 3x + 1 = 0 ⇒ . ⇒ x = 0,5; x = 1;
x = 0 — тут решать нечего.
Из трех чисел x = 0, x = 0,5 и x = 1 внутри отрезка [0,5; 5] лежит только x = 1, а число x = 0,5 является его концом. Имеем:
y(0,5) = 0,5 2 − 3·0,5 + ln 0,5 = ln 0,5 − 1,25;
y(1) = 1 2 − 3·1 + ln 1 = −2;
y(5) = 5 2 − 3·5 + ln 5 = 10 + ln 5.
Из полученных трех значений лишь y = −2 не содержит знака логарифма — это и будет ответ.
Задача. Найти наибольшее значение функции y = ln(6x) − 6x + 4 на отрезке [0,1; 3].
Выясняем, когда производная или ее знаменатель равны нулю:
y’ = 0 ⇒ 1 − 6x = 0 ⇒ x = 1/6;
x = 0 — уже решено.
Вычеркиваем число x = 0, поскольку оно лежит за пределами отрезка [0,1; 3]. Считаем значение функции на концах отрезка и в точке x = 1/6:
y(0,1) = ln(6·0,1) − 6·0,1 + 4 = ln 0,6 + 3,4;
y(1/6) = ln(6·1/6) − 6·1/6 + 4 = ln 1 + 3 = 3;
y(3) = ln(6·3) − 6·3 + 4 = ln 18 − 14.
Очевидно, только y = 3 может выступать в качестве ответа — остальные значения содержат знак логарифма и не могут быть записаны в бланк ответов.
http://poisk-ru.ru/s48502t1.html
http://www.berdov.com/ege/extremum/summary/
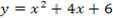
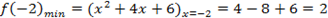
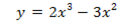
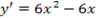
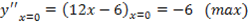
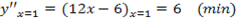
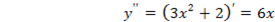
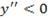
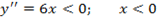
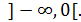
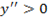
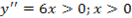
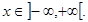
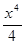
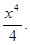
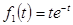 и
и 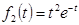 . Определить максимальные реакции на оба препарата и сравнить их.
. Определить максимальные реакции на оба препарата и сравнить их.