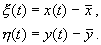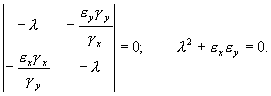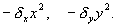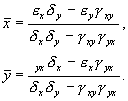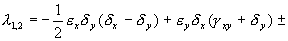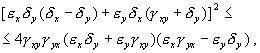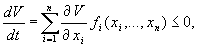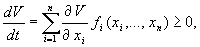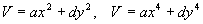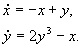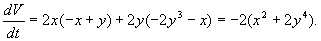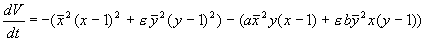Управляемость и наблюдаемость.
Рассмотрим два фундаментальных свойства систем управления, которые имеют такое же большое значение, как и свойство устойчивости. Первое из них связано с возможностью перевода системы из любого начального состояния в любое другое заданное состояние, а второе – с возможностью определить состояние системы по управляемой величине и управляющему воздействию.
Определение управляемости. Система (управляемая система или объект) с уравнением состояния
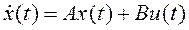
является полностью управляемой, если существует управляющий сигнал 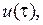
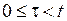
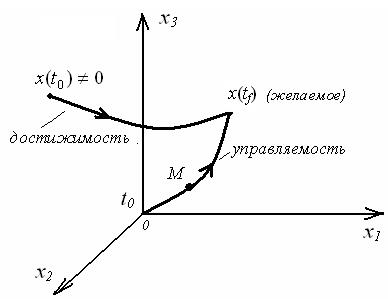
Здесь точка М – изображающая точка.
Изменение положения изображающей точки – это переход системы из одного состояния в другое.
Нетрудно показать, что если система полностью управляемая, то ее при некоторых допущениях можно перевести из любого начального состояния в любое другое состояние. Это свойство системы называют достижимостью.
Управляемость – частный случай достижимости.
На рисунке выше дана геометрическая интерпретация свойств управляемости и достижимости.
Теорема Калмана. (О полной управляемости).
Для полной управляемости системы, описываемой уравнением (1), необходимо и достаточно, чтобы матрица управляемости (блочная матрица)
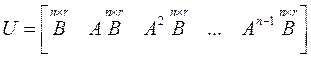
имела ранг, равный n, где n – порядок системы: 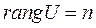
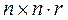
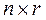

Если существует хотя бы один минор n-го порядка 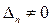
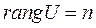
Для системы с одним входом, т.е. если 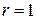
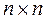
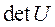
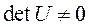
то есть матрица управляемости должна быть невырожденной.
Пример. Для двойного интегратора
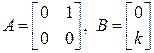
где k – коэффициент усиления двойного интегратора.
Является лидвойной интегратор полностью управляемым, и при каких условиях?
В данном случае n=2, 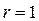
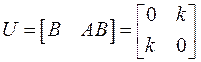
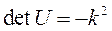
Следовательно, 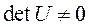
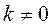
Команды Matlab: U=ctrb(A,B); r=rank(U).
Замечание 1. Физический смысл свойства полной управляемости заключается в том, что управление 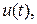
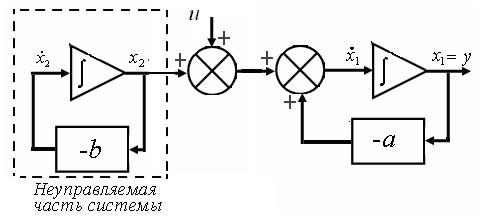
Замечание 2. Является ли система полностью управляемой можно определить с помощью операционной структурной схемы. Если на операционной структурной схеме имеются пути, ведущие от управления к каждой переменной состояния, то система является полностью управляемой.
Пример. Рассмотрим операционную структурную схему системы, представленную на рисунке ниже. Здесь 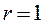
Как видим, управление u будет оказывать влияние лишь на переменную х1. Левая часть структурной схемы ведет себя автономно от управления u. Следовательно, система не является полностью управляемой. Если система не является полностью управляемой, то ее можно разложить на управляемую и неуправляемую части (подсистемы).
Аналитически покажем, что рассматриваемая система не является полностью управляемой. Для этого по структурной схеме найдем уравнения в переменных состояния
из которых видно, что управление u не влияет на х2 .


Отсюда матрица управляемости
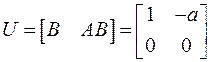
Как видим, 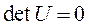
Замечание 3. Если система с одним входом, другими словами, при r=1, не является полностью управляемой, то ее ПФ вырождается, другими словами, ее ПФ является вырожденной ПФ, то есть порядок знаменателя ПФ будет меньше порядка системы (порядка характеристического уравнения системы).
Отсюда система с одним входом является полностью управляемой, если ее передаточная функция не содержит одинаковых сомножителей в числителе и знаменателе (сокращаемых сомножителей).
Для примера, рассмотренного в замечании 2:
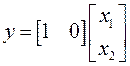
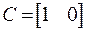
При этом ПФ системы
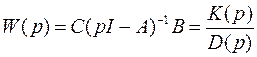
где характеристический многочлен
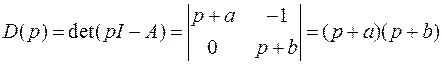
Следовательно, корни характеристического уравнения 

Найдем числитель 
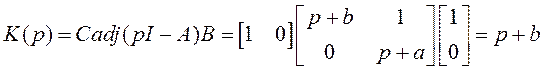
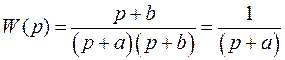
Порядок системы n=2, а порядок знаменателя ПФ равен 1, то есть передаточная функция системы вырождена. Эта система устойчива по начальным условиям, если 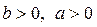
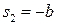
Модель в виде ПФ может быть только частичным описанием системы.
Замечание 4. Система, описываемая уравнением (1), называется стабилизируемой, если неуправляемая часть является устойчивой по начальным условиям. Для рассмотренного в замечании 2 примера условие стабилизируемости системы: 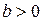
Свойство стабилизируемости позволяет за счет обратной связи обеспечить устойчивость замкнутой системы даже тогда, когда объект управления содержит неуправляемую часть. Включение неуправляемой части в модель системы достаточно общий случай. Это удобно для описания различных возмущающих воздействий. Например, постоянное возмущающее воздействие можно задать в пространстве состояний как 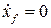
Замечание 5. Ранг матрицы управляемости не зависит от выбора вектора состояния. Другими словами, ранг матрицы управляемости является инвариантом, т.е.
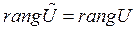
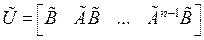
представляет собой матрицу управляемости преобразованной системы, описываемой
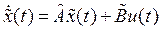
АИИК-испр 29-12-2015 (1). Конспект лекций введение. Понятие об автоматических системах
| Название | Конспект лекций введение. Понятие об автоматических системах |
| Дата | 05.10.2020 |
| Размер | 1.74 Mb. |
| Формат файла |  |
| Имя файла | АИИК-испр 29-12-2015 (1).docx |
| Тип | Конспект #141165 |
| страница | 3 из 5 |
 С этим файлом связано 1 файл(ов). Среди них: !СОП по температуре.doc. С этим файлом связано 1 файл(ов). Среди них: !СОП по температуре.doc.  Показать все связанные файлы Подборка по базе: Конспект лекций CREDO-технологии для решения геодезических задач, 4. конспект род собрания.docx, Опорный конспект Программное обеспечение компьютера.docx, №1 Введение.pdf, Правонарушение понятие и признаки.doc, Сложные эфиры и жиры — конспект.docx, 1 ПОНЯТИЕ И СОДЕРЖАНИЕ ПРЕДПРИНИМАТЕЛЬСТВА.docx, курс лекций транспортной психологии.docx, ТТП 121 ЗФ, Милостной М.Ю, Задание 4, конспект.pdf, экономика введение.odt Показать все связанные файлы Подборка по базе: Конспект лекций CREDO-технологии для решения геодезических задач, 4. конспект род собрания.docx, Опорный конспект Программное обеспечение компьютера.docx, №1 Введение.pdf, Правонарушение понятие и признаки.doc, Сложные эфиры и жиры — конспект.docx, 1 ПОНЯТИЕ И СОДЕРЖАНИЕ ПРЕДПРИНИМАТЕЛЬСТВА.docx, курс лекций транспортной психологии.docx, ТТП 121 ЗФ, Милостной М.Ю, Задание 4, конспект.pdf, экономика введение.odtА — функциональная матрица размером n x n, называемая матрицей состояния системы (объекта); В — функциональная матрица размером n x r, называемая матрицей управления (входа); С — функциональная матрица размером m x n, называемая матрицей выхода по состоянию; D — функциональная матрица размером m x r, называемая матрицей выхода по управлению. Матрица D отлична от нуля в случаях, когда в передаточной функции рассматриваемой системы порядок числителя равен порядку знаменателя. Поскольку в реальных системах порядок числителя, как правило, всегда меньше порядка знаменателя, матрица D считается равной нулю. Пример. На рис. 2. показан электродвигатель постоянного тока независимого возбуждения, работающий при постоянном магнитном потоке (Ф=const). Рис.2.Электродвигатель постоянного тока C*i=J где J – приведенный момент инерции электродвигателя. Выразим все уравнения относительно производных:
Таким образом для рассматриваемой системы матрицы А, В, С векторно-матричной модели будут иметь следующий вид:
Представляя векторы состояния, входа и выхода как Необходимым и достаточным условием асимптотической устойчивости линейной стационарной системы с уравнением состояния является отрицательность вещественных частей всех собст венных чисел матрицы А . Если в любой момент времени доступен для измерения вектор состояния, то на вход системы (1.1) может быть по дан сигнал где Устойчивость замкнутой системы (1.3) определяется собст венными числами матрицы А + ВК . Система (1.1) называется стабилизируемой при полной обратной связи, если существует матрица К коэффициентов усиления обратной связи такая, что замкнутая система (1.3) асимптотически устойчива. Пара матриц rank Невырожденность пары A , В достаточна для стабилизируе мости системы (1.1). Пример. Исследовать стабилизируемость системы с уравнением состояния Решение. Пара матриц А и В невырожденна, так как rank Поэтому система стабилизируема. Пример. Является ли стабилизируемой система с уравнением состояния Решение. Составим блочную матрицу Ее определитель равен минус единице, и поэтому ранг этой матрицы — три. Условие, выраженное равенством (1.4), является только достаточным, но не необходимым для стабидизируемости системы (1.1). Поэтому, если условие (1.4) не выполнено, делать заключение об отсутствии у системы (1.1) свойства стабилизируемости нельзя. Вопрос о стабилизируемости системы для которой условие (1.4) не выполнено, может быть решен приведением уравнения состояния (2.1) этой системы к канонической форме управляемости. Предположим, что ранг матрицы управляемости rank равен l. Тогда у этой матрицы есть l линейно независимых столбцов. Обозначим, через Остальные п—lстолбцов этой матрицы При замене вектора состояния х по формуле Матрицы где Обозначим вектор-столбец, образованный первыми lкомпонентами вектора состояния Ранг матрицы rank равен l. Поэтому подсистема, описываемая первым уравнением (2.6), управляема. На движение подсистемы с уравнением движения Уравнение (2.6) называют канонической формой управляемости для исходного уравнения состояния (2.1). Необходимым и достаточным условием стабилизируемости линейной стационарной системы (2.1) является отрицательность вещественных частей всех собственных чисел неуправляемой части. Другими словами, отрицательность вещественных частей всех собственных чисел матрицы A3 в канонической форме управляемости (2.4), (2.5) необходима и достаточна для стабилизируемости системы (2.1). Пример. Является ли стабилизируемой система с уравнением состояния Решение. Ранг этой матрицы равен 2. Система не является полностью управляемой. Приведем уравнение состояния к канонической форме управляемости: Рассмотрим линейную стационарную систему с одним входом и уравнением состояния Пусть для пары матриц в этом случае квадратная, условие (1.4) эквивалентно неравенству det Системе (3.1) при выполнении (3.2) можно за счет обратной связи вида (1.2) обеспечить любые наперед заданные собственные числа Здесь столбец dесть разность столбца p, образованного коэффициентами характеристического полинома системы (3.2), и столбца q, образованного коэффициентами полинома, имеющего заданные корни Матрица Fпостроена из нулей и коэффициентов полинома (3.5), исключая свободный член Если для системы с уравнением состояния (3.1) условие (1.4) не выполнено, то любые собственные числа можно обеспечить за счет обратной связи вида и=Кх только управляемой части этой системы. Например, система с уравнением состояния приведенная в предыдущем примере, имеет каноническую форму управляемости Рассмотрим отдельно управляемую часть и характеристический полином управляемой части Матрица (3.8) для управляемой части имеет вид а обратной к ней будет матрица Матрица (2.2) для управляемой части является в данном примере единичной Пусть требуется обеспечить управляемой части собственные числа В соответствии с (3.7) По формуле (3.3) находим Таким образом, нужная обратная связь имеет вид При приведении системы к канонической форме управляемости была выполнена замена переменной Неуправляемая часть рассмотренной системы имеет собственное число — 1. Обратная связь на это собственное число никак не влияет. Рассмотрим систему с уравнением состояния (1.1), стабилизированную обратной связью (1.2). Такая система описывается уравнением (1.3), и ее собственные движения затухают. Иногда качество стабилизации оценивается временем этого затухания. Обозначим матрицу Если система (3.9) при Зададимся положительным числом ε. Временем затухания собственного движения В некоторых случаях качество стабилизации оценивается временем затухания переходного процесса на выходе у=Сх системы (3.9). При этом временем переходного процесса Неравенство (3.11) эквивалентно неравенству Подставим в левую часть (3.12) выражение выходного сигнала через вектор состояния и обозначим симметричную матрицу За счет размещения собственных чисел достаточно далеко влево от мнимой оси можно добиться сколь угодно быстрого затухания переходного процесса при заданной точности, но при этом, прежде чем начнет выполняться неравенство (3.14), фазовый вектор Чтобы учесть ограничение на допустимый уровень управляющих воздействий где Q — положительно полуопределенная, а R — положительно определенная симметричные матрицы. Исследовать стабилизируемость системы с уравнением состоянияИССЛЕДОВАНИЕ УСТОЙЧИВОСТИ СТАЦИОНАРНЫХ СОСТОЯНИЙ НЕЛИНЕЙНЫХ СИСТЕМ ВТОРОГО ПОРЯДКА Метод Ляпунова линеаризации систем в окрестности стационарного состояния. Примеры исследования устойчивости стационарных состояний моделей биологических систем. Уравнения Лотки. Уравнения Вольтерра. Метод функции Ляпунова Пусть биологическая система описывается системой двух автономных дифференциальных уравнений второго порядка общего вида: Стационарные значения переменных системы определяются из алгебраических уравнений: Стационарные состояния соответствуют особым точкам дифференциального уравнения первого порядка, определяющего интегральные кривые: Математический анализ поведения траекторий этой системы на фазовой плоскости связан с именами французского математика Анри Пуанкаре и русского математика и механика Александра Михайловича Ляпунова (1857-1918). Ляпунов показал, что в большом числе случаев анализ устойчивости стационарного состояния нелинейной системы можно заменить анализом устойчивости системы, линеаризованной в окрестности стационарного состояния. Рассмотрим характер поведения переменных при некотором небольшом отклонении системы от состояния равновесия. Введем вместо переменных x, y новые независимые переменные x , h , определив их как смещения относительно равновесных значений переменных Подставив эти выражения в (5.1), получим: Предположим, что функции P и Q непрерывны и имеют непрерывные производные не ниже первого порядка. Тогда мы можем разложить правые части уравнений (5.5) в ряд Тейлора по переменным x , h . Учтем, что по определению особой точки и отбросим в уравнениях (5.6) нелинейные члены. Получим систему линейных уравнений с постоянными коэффициентами — систему первого приближения: Решение этой системы было рассмотрено в Лекции 4. Оно определяется корнями характеристического уравнения системы: Ляпунов показал, что в случае, если оба корня уравнения (5.9): имеют отличные от нуля действительные части, исследование уравнений первого приближения (5.8) всегда дает правильный ответ на вопрос о типе устойчивости состояния равновесия в системе (5.1). А именно: · если оба корня имеют отрицательную действительную часть и, следовательно, все решения уравнений первого приближения (5.8) затухают, то состояние равновесия устойчиво; · если хотя бы один корень имеет положительную действительную часть, то есть система (5.8) имеет нарастающие решения, то состояние равновесия неустойчиво. Если действительные части обоих корней характеристического уравнения равны нулю или если один корень равен нулю, а другой отрицателен, то уравнения (5.8) не дают ответа на вопрос об устойчивости состояния равновесия, и необходимо рассматривать члены более высокого порядка малости в разложении в ряд Тейлора правых частей уравнений (5.6). В случае, когда оба корня характеристического уравнения имеют отличные от нуля действительные части ( грубые с истемы), уравнение первого приближения определяют не только устойчивость стационарного состояния, но и характер фазовых траекторий в достаточно малой его окрестности. Как и в случае линейных уравнений (Лекция 4) здесь возможны пять типов грубых состояний равновесия: устойчивый узел, неустойчивый узел, устойчивый фокус, неустойчивый фокус и седло. Для исследования типов состояний равновесий удобно пользоваться диаграммой, изображенной на рис. 4.11. Для системы (5.1): Грубым состояниям равновесия соответствуют все точки плоскости параметров s , D , лежащие вне оси D =0 и полуоси s =0, D >0. Точкам оси D = 0 и полуоси s = 0, D >0 соответствуют негрубые состояния равновесия (негрубые особые точки). Их свойства могут быть изменены сколь угодно малыми изменениями правых частей уравнений (5.1) за счет сколь угодно малых изменений функций P(x,y), Q(x,y) и их производных. Поэтому характер негрубых состояний равновесия (в частности, устойчивость) уже не определяется значениями коэффициентов в правых частях уравнений первого приближения (5.8). В отличие от линейных систем, уже при небольших изменений в правых частях содержащихся там нелинейных членов может произойти качественное изменение фазового портрета — бифуркация. 1. Кинетические уравнения Лотки ( A . J . Lotka . Elements of Physical Biology, 1925) Лоткой была исследована гипотетическая химическая реакция: Модель очень простая и служит хорошей иллюстрацией применения исследования устойчивости стационарного состояния системы методом линеаризации. Пусть в некотором объеме находится в избытке вещество А. Молекулы А с некоторой постоянной скоростью Запишем систему уравнений, описывающих реакцию: Здесь x , y , B — концентрации химических компонентов. Первые два уравнения этой системы не зависят от B , поэтому их можно рассматривать отдельно. Рассмотрим стационарное решение системы: Из этих условий получим систему алгебраических уравнений, связывающих равновесные концентрации Координаты особой точки: Исследуем устойчивость этого стационарного состояния методом Ляпунова. Введем новые переменные x , h , характеризующие отклонения переменных от равновесных концентраций Линеаризованная система в новых переменных имеет вид: Отметим, что величины отклонений от стационарных значений переменных x , h могут менять знак, в то время как исходные переменные x , y , являющиеся концентрациями, могут быть только положительными. Запишем характеристическое уравнение системы (4.3): Корни характеристического уравнения: Фазовый портрет системы (5.13) изображен на рис. 5.1. Рис. 5.1. Фазовый портрет системы 5.13. а – устойчивый фокус , б – устойчивый узел. При Таким образом, в описанной выше химической реакции возможны разные режимы изменения переменных в зависимости от соотношения величин констант скоростей. Если Рис. 5.2 Плоскость параметров для системы 5.14. а – область устойчивого фокуса; б – область устойчивого узла |
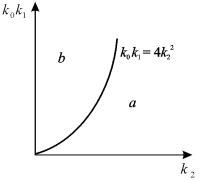
Соотношение параметров 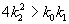
Рассмотрим плоскость параметров, где по оси абсцисс отложены значения константы k2, а по оси ординат – произведение k 0 k 1 . Парабола k 0 k 1 = 4 k 2 2 делит изображенную на рис. 5.2 плоскость параметров на две области – устойчивых узлов и устойчивых фокусов. Задавая те или иные значения параметров, можно получить колебательный и бесколебательный режимы изменения концентраций веществ x и y , и фазовый портрет системы, соответственно, будет собой представлять фокус (а) или узел (б), изображенные соответственно на рис 5.1 а, и 5.1 б.
Если в системе установятся стационарные концентрации веществ x и y , это приведет к установлению постоянной скорости прироста концентрации вещества В в третьем уравнении системы (5.13):
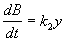
Ясно, что в действительности такая система реализоваться не может, так как в ней при t ® ¥ концентрация вещества В стремится к бесконечности. Однако система, подобная системе реакций Лотки, может представлять собой фрагмент более сложной химической системы. Исследованные нами уравнения правильно описывают поведение компонентов x и y , если приток вещества x (скорость его постоянна и равна k 0 ) осуществляется из большого «резервуара», а отток вещества y – в большой «резервуар» (значение В очень велико). При этих предположениях на малых промежутках времени (по сравнению с временем существенного изменения заполненности емкости B ) наше рассмотрение является вполне правомерным.
2. Модель Вольтерра
В качестве второго примера рассмотрим классическую модель взаимодействия видов, которая впервые была предложена В. Вольтерра в тридцатые годы XX века для объяснения периодических изменений числа особей, так называемую вольтерровскую модель «хищник-жертва». Более подробно модели взаимодействия видов мы рассмотрим в Лекции 9.
Пусть в некотором замкнутом районе живут хищники и жертвы, например, зайцы и волки. Зайцы питаются растительной пищей, имеющейся всегда в достаточном количестве. Волки могут питаться лишь зайцами. Обозначим число зайцев (жертв) x, а число волков (хищников) – y . Так как количество пищи у зайцев неограниченно, мы можем предположить, что они размножаются со скоростью, пропорциональной их числу:
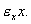
Если рождаемость зайцев превышает их смертность, e > 0. Выражение (5.16) соответствует автокаталитической реакции первого порядка.
Пусть убыль зайцев пропорциональна вероятности встречи зайца с волком, т.е. пропорциональна произведению численностей xy . Можно предположить по аналогии с бимолекулярными реакциями, где вероятность появления новой молекулы пропорциональна вероятности встречи двух молекул, что и количество волков нарастает тем быстрее, чем чаще происходят их встречи с зайцами, а именно, пропорционально xy .
Кроме того, имеет место процесс естественной смертности волков, причем скорость смертности пропорциональна их количеству.
Эти рассуждения приводят к системе уравнений для изменений численности зайцев-жертв x и волков-хищников y.
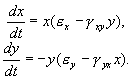
Покажем, что система уравнений (5.17) имеет на фазовой плоскости переменных xy ненулевую особую точку типа центр. Координаты этой особой точки 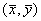
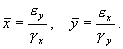
Так как все параметры 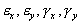
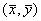
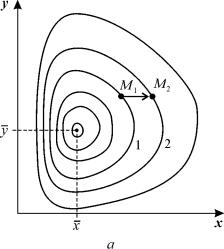
Рис. 5.3. Фазовый портрет системы 5.17. Особая точка типа «центр».
а – параметры системы: e x = 4, g xy = 0,3, e y = g yx = 0,4
б – параметры системы: e x =2, g xy = 0,3, e y = g yx = 0,4
Здесь x , h — отклонения 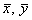
Характеристическое уравнение системы (5.18):
Корни этого уравнения чисто мнимые:
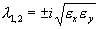
Таким образом, исследование системы показывает, что траектории вблизи особой точки являются концентрическими эллипсами, а сама особая точка – центром. Рас c матриваемая модель Вольтерра и вдали от особой точки имеет замкнутые траектории, хотя форма этих траекторий уже отличается от эллипсоидальной, и определяется параметрами системы (рис. 5.3).
Изменения численности жертвы и хищника во времени представляют собой колебания, причем колебания численности хищника отстают по фазе от колебаний жертв.
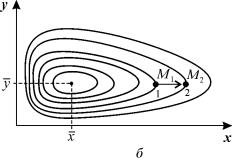
Как мы уже отмечали в Лекции 4, особая точка типа центр устойчива по Ляпунову, но не асимптотически. Покажем на данном примере, в чем это проявляется. Пусть колебания x ( t ) и y ( t ) происходят таким образом, что изображающая точка движется по фазовой траектории 1 (рис 5.3).
В момент, когда точка находится в положении М1, в систему добавляется извне некоторое число особей y такое, что изображающая точка переходит скачком из точки M 1 в точку M 2 . Если после этого систему предоставить самой себе, колебания x ( t ) , y ( t ) уже будут происходить с большими амплитудами, чем прежде, и изображающая точка будет двигаться по траектории 2. Это и означает, что колебания в системе неустойчивы: они навсегда изменяют свои характеристики при внешнем воздействии.
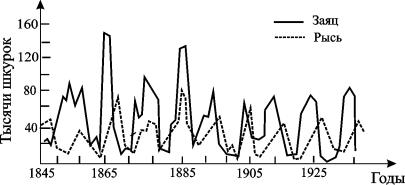
Рис. 5.4. Кривые численности зайца и рыси в Канаде
(по К. Вилли, В. Детье, 1974)
В дальнейшем мы рассмотрим модели, описывающие устойчивые колебательные режимы, и покажем, что на фазовой плоскости такие асимптотически устойчивые периодические движения описываются предельными циклами.
На рис. 5.4 кривые колебаний численности пушных зверей по данным компании Гудзонова залива о числе заготовленных шкурок. Во всех классических учебниках в течение многих лет колебательный характер этих изменений приводили как подтверждение гипотез, положенных в основу модели Вольтерра, которую мы только что рассмотрели. Действительно, периоды колебаний численности зайцев (жертв) и рысей (хищников) примерно одинаковы и составляют порядка 9 – 10 лет. При этом максимум численности зайцев опережает, как правило, максимум численности рысей на один год. Можно полагать, что мы видим регулярные колебания, осложненные случайными факторами, связанными с погодой и проч.
Однако возможна и другая интерпретация этих данных наблюдений на основе моделей детерминированного хаоса. О дискретных моделях такого типа мы уже говорили в Лекции 3. Непрерывные модели популяционной динамики, приводящие к детерминированному хаосу, мы рассмотрим в Лекции 9.
Серьезным недостатком рассмотренной модели Вольтерра является неустойчивость решений по отношению к малым случайным воздействиям, приводящим к изменению переменных. Кроме того, в силу «негрубости» этой системы произвольно малое изменение вида правых частей уравнений (величин параметров системы) приведет к изменению типа особой точки, и, следовательно, к изменению характера фазовых траекторий.
Поскольку природные системы подвергаются огромному количеству случайных воздействий, реалистическая модель должна быть по отношению к ним устойчивой. Поэтому негрубые системы не могут давать адекватное описание природных явлений.
Различные модификации рассмотренной нами системы, изученные самим Вольтерра и другими авторами, лишены этих недостатков. Наиболее широко известные из них будут рассмотрены в Лекции 9. Здесь мы остановимся на модели, которая учитывает самоограничение в росте обеих популяций. На ее примере видно, как может меняться характер решений при изменении параметров системы.
Итак, рассмотрим систему:
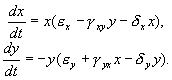
Система (5.19) отличается от ранее рассмотренной системы наличием в правых частях членов:
Эти члены отражают тот факт, что численность популяции жертв не может расти до бесконечности даже в отсутствие хищников в силу ограниченности пищевых ресурсов, ареала существования и проч. Такие же «самоограничения» накладываются на популяцию хищников.
Система имеет два стационарных решения: нулевое и ненулевое. Анализ показывает, что нулевое решение представляет собой неустойчивый узел. Рассмотрим систему алгебраических уравнений, решение которых дает координаты ненулевого стационарного состояния.
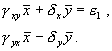
Корни характеристического уравнения системы, линеаризованной в окрестности особой точки:
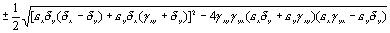
Из выражения для характеристических чисел видно, что если выполнено условие

то численности хищников и жертв совершают во времени затухающие колебания. Система имеет особую точку – устойчивый фокус.
Рис. 5.5. Фазовый портрет системы 5.19
а – устойчивый фокус,
б – устойчивый узел,
При изменении знака неравенства на обратный точка становится устойчивым узлом.
И в том и в другом случае стационарное состояние асимптотически устойчиво, и решение устойчиво к малым изменениям правых частей уравнений. Таким образом, самоограничение популяции приводит к устойчивости ее численности.
Важно отметить, что простейшие вольтерровские модели, которые мы рассмотрели, не могут описывать устойчивые колебания с постоянными периодом и амплитудой. Для описания таких колебаний необходимы нелинейные модели, имеющие на фазовой плоскости предельный цикл . Они будут рассмотрены в Лекции 8.
МЕТОД ФУНКЦИЙ ЛЯПУНОВА ИССЛЕДОВАНИЯ УСТОЙЧИВОСТИ СТАЦИОНАРНОГО СОСТОЯНИЯ.
При аналитическом исследовании устойчивости стационарного состояния часто используется метод подбора функции, линии уровня которой представляют собой замкнутые траектории – «ловушки» для фазовых траекторий системы типа (5.1)
Этот метод применим к автономной системе уравнений n -го порядка
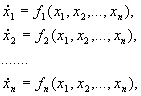
Он состоит в непосредственном исследовании устойчивости ее стационарного состояния при помощи подходящим образом подобранной функции Ляпунова 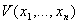
Метод основан на двух теоремах.
Если существует дифференцируемая функция V ( x 1 ,…, xn ), удовлетворяющая в окрестности начала координат следующим условиям:
б)
причем 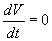
то точка покоя системы (5.21) устойчива.
Если существует дифференцируемая функция V ( x 1 ,…, xn ), удовлетворяющая в окрестности начала координат следующим условиям:
a ) V ( x 1 ,…, xn ) = 0 и сколь угодно близко от начала координат имеются точки, в которых V ( x 1 ,…, xn ) > 0;
б)
причем 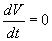
то точка покоя системы (5.21) неустойчива.
С доказательством этих теорем можно познакомиться в книге Л.Э. Эльсгольц «Теория дифференциальных уравнений» или в других учебниках по теории дифференциальных уравнений.
Общего методы построения функции Ляпунова не существует. Однако для линейных автономных систем ее следует искать в виде:
и т.п., подбирая надлежащим образом коэффициенты a > 0 , b > 0. Для нелинейных систем a и b могут быть произвольных знаков.
1. Рассмотрим линейную систему:
Выберем функцию Ляпунова: V = x 2 + y 2 . Тогда
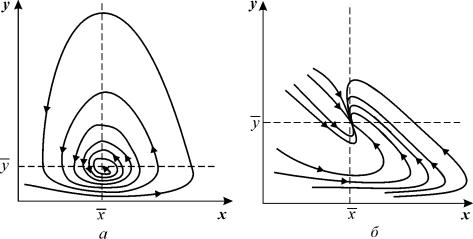
Это выражение всегда отрицательно при х ¹ 0 , т.к. в скобках стоят четные степени x . Следовательно, точка (0, 0) устойчива.
2. Рассмотрим систему уравнений, описывающую конкуренцию видов, численности которых x и y . Каждый из видов размножается в соответствии с логистическим законом, а при встрече (произведения в правых частях уравнений), численность как одного, так и другого вида уменьшается.
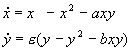
Исследуем стационарное состояние, соответствующее сосуществованию видов ( ` x , ` y ) – ненулевое для x и y . Его координаты:
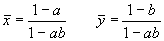
В. Вольтерра показал, что стационарное состояние (5.23) устойчиво для параметров системы a > 0, b £ 1 , построив функцию Ляпунова:
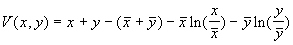
Ее производная равна
и отрицательна при малых значениях коэффициентов a , b и x , y > 0. Доказательство приведено в книге В. Вольтерра. «Математическая теория борьбы за существование» (М., 1976)
Ризниченко Г.Ю., Рубин А.Б. Математические модели биологических продукционных процессов. М., изд. МГУ, 1993
Вольтерра В. Математическая теория борьбы за существование М., Наука, 1976
Эльсгольц Л.Э. Теория дифференциальных уравнений. М., Наука, 1971
http://topuch.ru/konspekt-lekcij-vvedenie-ponyatie-ob-avtomaticheskih-sistemah/index3.html
http://www.library.biophys.msu.ru/LectMB/Lect05.htm
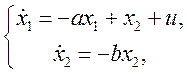


 (t)=
(t)=  i(t) +
i(t) +  + CΩ
+ CΩ =Ω
=Ω =
=  —
—  матрицы равен нулю; коэффициент при токе равен С/J, соответственно коэффициент
матрицы равен нулю; коэффициент при токе равен С/J, соответственно коэффициент  матрицы равен C/J; множитель угла поворота так же отсутствует, соответственно
матрицы равен C/J; множитель угла поворота так же отсутствует, соответственно  равен нулю.
равен нулю. равен нулю; Mc=C*i, соответственно коэффициент при моменте из первого уравнения равен 1/J, отсюда
равен нулю; Mc=C*i, соответственно коэффициент при моменте из первого уравнения равен 1/J, отсюда  .
.
 получим следующую векторно-матричную модель электродвигателя постоянного тока:
получим следующую векторно-матричную модель электродвигателя постоянного тока:
 (1.1)
(1.1) , (1.2)
, (1.2) — некоторое внешнее воздействие. В результате подстановки (1.2) в (1.1) получаем уравнение состояния замкнутой системы
— некоторое внешнее воздействие. В результате подстановки (1.2) в (1.1) получаем уравнение состояния замкнутой системы (1.3)
(1.3) и
и  называется невырож денной при выполнении условия
называется невырож денной при выполнении условия (1.4)
(1.4)
 rank
rank 


 =l (2.2)
=l (2.2) линейно независимые столбцы матрицы S. Пусть матрица Т в качестве первых l столбцов имеет столбцы
линейно независимые столбцы матрицы S. Пусть матрица Т в качестве первых l столбцов имеет столбцы  (2.3)
(2.3) выбираются произвольно, но так, чтобы det
выбираются произвольно, но так, чтобы det 
 для нового вектора состояния
для нового вектора состояния  получаем уравнение
получаем уравнение (2.4)
(2.4) и
и  имеют следующую структуру:
имеют следующую структуру:





 , через
, через  , а вектор-столбец, образованный последующими
, а вектор-столбец, образованный последующими  компонентами, через
компонентами, через  .Тогда уравнение состояния (2.4) с учетом этого обозначения и равенств (2.5) распадается на два:
.Тогда уравнение состояния (2.4) с учетом этого обозначения и равенств (2.5) распадается на два: (2.6)
(2.6)
 =l (2.7)
=l (2.7) управление не влияет. Она неуправляема.
управление не влияет. Она неуправляема.







 асимптотически устойчива. Система стабилизируема.
асимптотически устойчива. Система стабилизируема. и
и  выполнено условие (1.4). Так как матрица
выполнено условие (1.4). Так как матрица
 (3.2)
(3.2) Для этого матрицу К коэффициентов усиления в цепи обратной связи можно выбрать по формуле
Для этого матрицу К коэффициентов усиления в цепи обратной связи можно выбрать по формуле (3.3)
(3.3) (3.4)
(3.4) (3.5)
(3.5) (3.6)
(3.6) (3.7)
(3.7) ,
, . (3.8)
. (3.8)




 .
.
 и
и  которым отвечает полином
которым отвечает полином 



 Выполним теперь обратную замену:
Выполним теперь обратную замену:
 через
через  и запишем уравнение собственных движений системы (1.3) в виде
и запишем уравнение собственных движений системы (1.3) в виде (3.9)
(3.9) находится в состоянии
находится в состоянии  , то для
, то для  ее состояние меняется по закону
ее состояние меняется по закону , при
, при  (3.10)
(3.10) будем называть время, начиная с которого не нарушается неравенство
будем называть время, начиная с которого не нарушается неравенство 
 (3.11)
(3.11)
 (3.12)
(3.12) (3. 13)
(3. 13) через Q. Тогда временем переходного процесса
через Q. Тогда временем переходного процесса  при
при  становится и остается в дальнейшем меньше
становится и остается в дальнейшем меньше 
 (3.14)
(3.14) в некоторые моменты может значительно превосходить по норме
в некоторые моменты может значительно превосходить по норме  (3.15)
(3.15) качество процесса стабилизации оценивают величиной интеграла
качество процесса стабилизации оценивают величиной интеграла (3.16)
(3.16)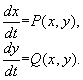 (5.1)
(5.1)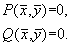 (5.2)
(5.2)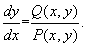 (5.3)
(5.3)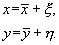 (5.4)
(5.4)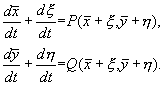 (5.5)
(5.5)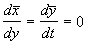 , так как
, так как 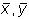 — координаты особой точки.
— координаты особой точки.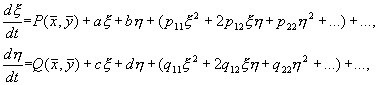 (5.6)
(5.6)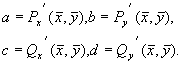 (5.7)
(5.7)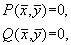
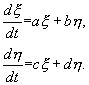 (5.8)
(5.8)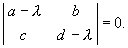 (5.9)
(5.9)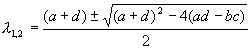 (5.10)
(5.10)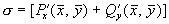 ,
,  (5.11)
(5.11)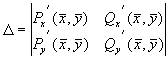 . (5.12)
. (5.12)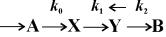
 превращаются в молекулы вещества X (реакция нулевого порядка). Вещество X может превращаться в вещество Y, причем скорость этой реакции тем больше, чем больше концентрация вещества Y – реакция второго порядка. В схеме это отражено обратной стрелкой над символом Y. Молекулы Y в свою очередь необратимо распадаются, в результате образуется вещество B (реакция первого порядка).
превращаются в молекулы вещества X (реакция нулевого порядка). Вещество X может превращаться в вещество Y, причем скорость этой реакции тем больше, чем больше концентрация вещества Y – реакция второго порядка. В схеме это отражено обратной стрелкой над символом Y. Молекулы Y в свою очередь необратимо распадаются, в результате образуется вещество B (реакция первого порядка).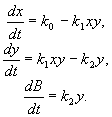 (5.13)
(5.13)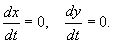
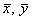 :
: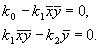 (5.14)
(5.14)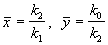 .
.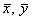 :
: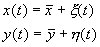 .
.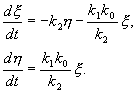 (5.15)
(5.15)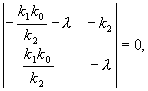
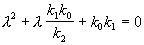 .
.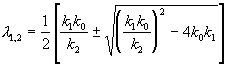 .
.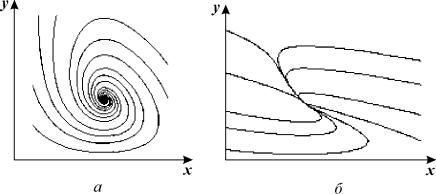
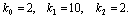
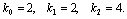
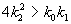 подкоренное выражение отрицательно, и особая точка – фокус, при обратном соотношении – узел. И в том и в другом случае особая точка устойчива, так как действительная часть обоих корней характеристического уравнения отрицательна.
подкоренное выражение отрицательно, и особая точка – фокус, при обратном соотношении – узел. И в том и в другом случае особая точка устойчива, так как действительная часть обоих корней характеристического уравнения отрицательна.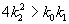 , имеют место затухающие колебания концентраций компонентов, при
, имеют место затухающие колебания концентраций компонентов, при 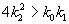 – бесколебательное приближение концентраций к стационарным.
– бесколебательное приближение концентраций к стационарным.