Курсовая работа: Итерационные методы решения систем линейных алгебраических уравнений
Данная курсовая работа включает в себя три итерационных метода решения систем линейных алгебраических уравнений (СЛАУ):
1. Метод Якоби (метод итераций).
2. Метод Холецкого.
3. Метод верхней релаксации.
Также данная курсовая работа включает в себя: описание метода, применение метода к конкретной задаче (анализ), код программы решения вышеперечисленных методов на языке программирования BorlandC++ Builder 6.
Метод решения задачи называют итерационным , если в результате получают бесконечную последовательность приближений к решению. Основное достоинство итерационных методов состоит в том, что точность искомого решения задается. Число итераций, которое необходимо выполнить для получения заданной точности 
Главным недостатком этих методов является то, что вопрос сходимости итерационного процесса требует отдельного исследования. Примером обычных итерационных методов служат: метод итераций (метод Якоби), метод Зейделя, метод верхних релаксаций.
Начнем с метода итераций или как его ещё называют метода Якоби.
Существует сиcтема A·x = f (1), где матрица A = [aij ] (i, j = 1, 2, …m ) имеет обратную матрицу; x = (x1 , x2 , x3 ,… xm ) – вектор неизвестных, f – вектор свободных членов. Систему (1) нужно преобразовать к следующему виду: 



Значение суммы считается равным 0, если верхний предел суммирования меньше нижнего. Тогда при i=1 уравнение имеет вид: 

Начальные значения 



Если последовательность приближений x1 (0) , x2 (0) ,…, xm (0) , x1 (1) , x2 (1) ,…, xm (1) ,…, x1 (k) , x2 (k) ,… , xm (k) имеет предел 

Достаточным условием сходимости решения системы (1) является то, что матрица A является матрицей с преобладающими диагональными элементами, то есть 
Теперь рассмотрим второй итерационный метод – метод Зейделя , который является модификацией метода Якоби. Основная его идея заключается в том, что при вычислении (k +1) – го приближения неизвестной xi учитываются уже вычисленные ранее (k +1) – е приближения (x1 x2 ,…, xi-1 ).
Пусть дана приведенная линейная система: 
Предполагается, что k -е приближение 
|
Если выполняется достаточное условие сходимости для системы (5) – по строкам, то в методе Зейделя выгодно расположить уравнения (6) так, чтобы первое уравнение системы имело наименьшую сумму модулей коэффициентов: 
Теперь рассмотри 3 метод – метод верхних релаксаций .
Метод верхней релаксации – это есть метод Зейделя с заданным числовым параметром w.
Одним из наиболее распространенных одношаговых методов является метод верхних релаксаций, который имеет следующий вид 
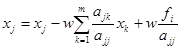
Действительно, при последовательном нахождении элемента 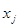
Курсовая работа: Итерационные методы решения систем линейных алгебраических уравнений
| Название: Итерационные методы решения систем линейных алгебраических уравнений Раздел: Рефераты по математике Тип: курсовая работа Добавлен 16:36:13 02 декабря 2009 Похожие работы Просмотров: 438 Комментариев: 20 Оценило: 4 человек Средний балл: 4.3 Оценка: неизвестно Скачать | |
|
Если выполняется достаточное условие сходимости для системы (5) – по строкам, то в методе Зейделя выгодно расположить уравнения (6) так, чтобы первое уравнение системы имело наименьшую сумму модулей коэффициентов: 
Теперь рассмотри 3 метод – метод верхних релаксаций .
Метод верхней релаксации – это есть метод Зейделя с заданным числовым параметром w.
Одним из наиболее распространенных одношаговых методов является метод верхних релаксаций, который имеет следующий вид 

Действительно, при последовательном нахождении элемента 
Итерационные методы решения систем линейных уравнений курсовая
Системы линейных уравнений
1. Теоретическая часть
1.1 Основные понятия и теоремы систем линейных уравнений
1.1.1 Критерий совместности общей системы линейных уравнений
1.1.2 Однородная система п линейных уравнений с n неизвестными
1.1.3 Структура общих решений однородной и неоднородной системы уравнений
1.2 Основные методы решения систем линейных уравнений
1.2.1 Матричный метод решения систем линейных уравнений
1.2.2 Метод Крамера
1.2.3 Метод Гаусса
1.4 Ответы на теоретические вопросы
Курс «Алгебра и геометрия» занимает особенное место в системе математической дисциплины, которая изучается студентами специальностей ПМ, САУ и IНФ, как базовый курс. Наверное, нет ни одной математической дисциплины, в которой бы не применялись понятия алгебры и геометрии.совая работа должна способствовать более углубленному изучению курса «Алгебра и геометрия», осмыслению его и применению для решения задачи практического содержания.
Данная работа содержит раскрытие вопроса решения систем линейных алгебраических уравнений, способы получения результата и применение систем для решения экономических задач.
Работа состоит из двух частей — теоретической и практической. В теоретической части приведены определения таких понятий, как система линейных уравнений, общее и частное решения, совместность и несовместность систем, однородные и неоднородные системы, рассмотрены различные методы решения систем уравнений. Также даны ответы на теоретические вопросы.
В практической части решены системы линейных уравнений, а также рассмотрены экономические задачи, решение которых сводится к решению соответствующей системы.
система линейное уравнение
1. Теоретическая часть
1.1 Основные понятия и теоремы систем линейных уравнений
В самом общем случае система линейных уравнений имеет следующий вид:
a11x1 + a12x2 + …+ a1n xn = b1;x1 + a22x2 + …+ a2n xn = b2;
где х1, х2, …, хn — неизвестные, значения которых подлежат нахождению. В общем случае число неизвестных не обязательно должно быть равно числу уравнений самой системы. Числа а11, а12, …, аmn называются коэффициентами системы, а b1, b2, …, bm — её свободными членами. Для удобства коэффициенты системы аij (i = 1, 2. m; j = 1, 2. n) и свободные члены bi (i=1, 2. m) снабжены индексами. Первый индекс коэффициентов аij соответствует номеру уравнения, а второй индекс — номеру неизвестной хi, при которой коэффициент поставлен. Индекс свободного члена bi соответствует номеру уравнения, в которое входит bi.
Дадим определения некоторых понятий, необходимых при изучении системы уравнений. Решением системы уравнений называется всякая совокупность чисел ?1, ?2, ?n, которая будучи поставлена в систему на место неизвестных х1, х2, …, хn, обращает все уравнения системы в тождества. Система уравнений называется совместной, если она имеет хотя бы одно решение, и несовместной, если не имеет решений. Совместная система уравнений называется определенной, если она имеет одно единственное решение, и неопределенной, если она имеет по крайней мере два различных решения.
Две системы уравнений называются равносильными или эквивалентными, если они имеют одно и тоже множество решений.
Наша задача будет заключаться в нахождении решений системы. При этом могут возникнуть три ситуации:
. Система может иметь единственное решение.
2. Система может иметь бесконечное множество решений.
. И третий случай, когда система вообще не имеет решения.
.1.1 Критерий совместности общей системы линейных уравнений
Как уже было отмечено, под общей системой линейных уравнений мы понимаем систему, в которой число неизвестных необязательно совпадает с числом уравнений.
Пусть дана общая система линейных уравнений и требуется установить признак существования решения этой системы, т.е. условия, при которых система является совместной.
Из коэффициентов при неизвестных и свободных членов системы составим матрицу
которую назовем основной матрицей системы, и матрицу
a11 a12 … a1n b1
a21 a22 … a2n b2
B = ……………………… ……,am2 … amn bm
которую назовем расширенной матрицей системы.
Теорема (Теорема Кронекера — Капелли) Для того чтобы система линейных неоднородных уравнений была совместной, необходимо и достаточно, чтобы ранг расширенной матрицы системы был равен рангу ее основной матрицы.
Пусть система совместна и c1, c2. сп — некоторое ее решение. Тогда имеют место равенства:
а11с1 + а12с2 + …+ а1nсn = b1;
а21с1 + а22с2 + …+ а2nсn = b2;
аm1с1 + аm2с2 + …+ аmnсn = bm
из которых следует, что последний столбец расширенной матрицы есть линейная комбинация остальных ее столбцов с коэффициентами с1, с2. сп. Согласно предложению, последний столбец матрицы В может быть вычеркнут без изменения ее ранга. При этом мы из матрицы В получим матрицу А. Таким образом, если ci, cz. сп — решение системы уравнении, то rang А = rang В.
Достаточность. Пусть теперь rang A = rang В. Покажем, что при этом система уравнений совместна. Рассмотрим r базисных столбцов матрицы А. Очевидно, что они будут базисными столбцами и матрицы В. Согласно теореме о базисных строках и столбцах, последний столбец матрицы В можно представить как линейную комбинацию базисных столбцов, а следовательно, как линейную комбинацию всех столбцов матрицы А, т.е.
b1 = а11с1 + а12с2 + …+ а1nсn;= а21с1 + а22с2 + …+ а2nсn;
где c1, c2. сп — коэффициенты линейных комбинаций. Таким образом, системе удовлетворяют значения x1 = c1. хп = сп, следовательно, она совместна. Теорема доказана.
1.1.2 Однородная система п линейных уравнений с n неизвестными
Линейное уравнение называется однородным, если его свободный член равен нулю. Система линейных уравнений называется однородной, если все входящие в нее уравнения являются линейными однородными уравнениями.
Однородная система п линейных уравнений с п неизвестными имеет вид:
а11х1 + а12х2 + …+ а1nхn = 0;
а21х1 + а22х2 + …+ а2nхn = 0;
аn1х1 + аn2х2 + …+ аnnхn = 0.
Непосредственной проверкой убеждаемся в том, что однородная система линейных уравнений имеет нулевое решение: х1 = 0, х2 = 0. хп = 0.
Таким образом, однородная система линейных уравнений всегда совместна. Поэтому важно выяснить, при каких условиях она является определенной. Покажем, что однородная система п линейных уравнений с п неизвестными имеет ненулевые решения тогда и только тогда, когда определитель ее равен нулю.
В самом деле, пусть D = 0. Так как однородная система уравнений является частным случаем неоднородной системы, то к ней применимо правило Крамера. Но для однородной системы все D xi = 0, так как каждый из этих определителей содержит столбец из нулей (bi = 0). Поэтому система, равносильная системе, будет иметь вид D x1= 0, D x2=0;., D xn= 0
Из этой системы следует, что однородная система имеет единственное нулевое решение, если ? 0; если же D = 0, то из условий следует, что она имеет бесчисленное множество решений.
Теорема. Для заданной однородной системы уравнений , для которой , где — число неизвестных, существует линейно независимых решений и любое решение системы представляется в виде линейной комбинации этих решений.
Максимальное число линейно независимых решений однородной системы называется фундаментальной системой решений этой системы уравнений.
— фундаментальная система решений однородной системы уравнений (Ф.С. Р.). Она содержит решений и получается с общего решения, если свободным переменным придавать последовательно значения: . Полученная таким образом фундаментальная система называется нормированной.
Обратим внимание, что решение однородных систем осуществляется теми же методами, что и неоднородных.
1.1.3 Структура общих решений однородной и неоднородной системы уравнений
Теорема 1. Общие решения однородной системы уравнений
, где , — число неизвестных, представляется в виде:
где — свободные постоянные, , — фундаментальная система решений.
Теорема 2. Общие решения неоднородной системы уравнений
представляется в виде:
где — некоторое частное решение неоднородной системы, — общее решение соответствующей однородной системы.
.2 Основные методы решения систем линейных уравнений
1.2.1 Матричный метод решения систем линейных уравнений
Матрицы дают возможность кратко записать систему линейных уравнений. Пусть дана система из 3-х уравнений с тремя неизвестными:
Рассмотрим матрицу системы
и матрицы столбцы неизвестных и свободных членов
т.е. в результате произведения мы получаем левые части уравнений данной системы. Тогда пользуясь определением равенства матриц данную систему можно записать в виде
Здесь матрицы A и B известны, а матрица X неизвестна. Её и нужно найти, т.к. её элементы являются решением данной системы. Это уравнение называют матричным уравнением.
Пусть определитель матрицы отличен от нуля |A| ? 0. Тогда матричное уравнение решается следующим образом. Умножим обе части уравнения слева на матрицу A-1, обратную матрице A: . Поскольку A-1A = E и E?X = X, то получаем решение матричного уравнения в виде X = A-1B.
Заметим, что поскольку обратную матрицу можно найти только для квадратных матриц, то матричным методом можно решать только те системы, в которых число уравнений совпадает с числом неизвестных. Однако, матричная запись системы возможна и в случае, когда число уравнений не равно числу неизвестных, тогда матрица A не будет квадратной и поэтому нельзя найти решение системы в виде X = A-1B.
Рассмотрим систему 3-х линейных уравнений с тремя неизвестными:
Определитель третьего порядка, соответствующий матрице системы, т.е. составленный из коэффициентов при неизвестных,
называется определителем системы.
Составим ещё три определителя следующим образом: заменим в определителе D последовательно 1, 2 и 3 столбцы столбцом свободных членов
Тогда можно доказать следующий результат.
Теорема (правило Крамера). Если определитель системы ? ? 0, то рассматриваемая система имеет одно и только одно решение, причём
Доказательство. Итак, рассмотрим систему 3-х уравнений с тремя неизвестными. Умножим 1-ое уравнение системы на алгебраическое дополнение A11 элемента a11, 2-ое уравнение — на A21 и 3-е — на A31:
Сложим эти уравнения:
Рассмотрим каждую из скобок и правую часть этого уравнения. По теореме о разложении определителя по элементам 1-го столбца
Далее рассмотрим коэффициенты при x2:
Аналогично можно показать, что и .
Наконец несложно заметить, что
Таким образом, получаем равенство: .
Аналогично выводятся равенства и , откуда и следует утверждение теоремы.
Таким образом, заметим, что если определитель системы ? ? 0, то система имеет единственное решение и обратно. Если же определитель системы равен нулю, то система либо имеет бесконечное множество решений, либо не имеет решений, т.е. несовместна.
Метод Гаусса основывается на следующей теореме: элементарным преобразованиям строк расширенной матрицы системы отвечает превращение этой системы в эквивалентную.
С помощью элементарных преобразований строки расширенной матрицы, а также перемены местами столбцов, что отвечает перепозначенню переменной, матрица сводится к ступенчатой (или трапециевидной) форме. Этой матрице ставится в соответствие система, эквивалентная исходной. Это прямой ход метода Гаусса. Решение полученной системы осуществляется снизу вверх (обратный ход метода Гаусcа).
Более детально этот процесс выглядит так: матрица в результате элементарных преобразований принимает такой вид:
Тогда возможны несколько случаев:
. Хотя б одно с чисел отличное от нуля, тогда і система несовместная.
а) , система совместная, имеет единственное решение;
б) , система совместная, имеет бесконечное множество решений.
В случае совместимости системы, ставим последней матрице в соответствие систему уравнений вида
Эту систему переписываем, оставляя базисные переменные слева, свободные — справа
Именно эту систему решаем, начиная снизу вверх.
В результате получаем или единственное решение, или множество решений, которые записываются в виде общего решения.
Метод Гаусса представляет собой метод последовательного исключения переменной. Вычислительная процедура гауссових исключений может быть формализирована с помощью простых правил.
Назовем переменную, которая исключалась, разрешающей, коэффициент при ней — разрешающим элементом, строку и столбец матрицы, в которой размещен разрешающий элемент — разрешающими.
Перечисление элементов расширенной матрицы при выполнении элементарных преобразований выполняется по таким правилам:
) элементы разрешающей строки и всех вышерасположенных строк остаются неизменными;
) элементы разрешающего столбца, которые расположены ниже разрешающего элемента, обращаются в нуль;
) все другие элементы матрицы вычисляются по правилу прямоугольника: преобразовываемый элемент равняется разности произведений элементов главной и побочной диагонали.
Тут — разрешающий элемент, — преобразуемый элемент. Обозначим — элемент, который получен вычислением по правилу прямоугольника. Тогда
Модификацией метода Гаусса является метод полного исключения или метод Жордана — Гаусса.
Метод полного исключения (метод Жордана-Гаусса) заключается в том, что в результате преобразований расширенной матрицы в ней выделяется диагональная подматриця и тогда решение исходной системы выписывается просто.
Метод полного исключения работает за такими правилами:
) назначается разрешающий элемент; им будет коэффициент при неизвестной, которая исключается;
) элементы разрешающей строки остаются неизменными;
) все элементы разрешающего столбца (кроме разрешающего элемента) заменяются нулями и остаются такими до конца преобразований;
) все другие элементы матрицы пересчитываются по правилу прямоугольника.
Метод полного исключения может быть использован для обращения матрицы (известен также под названием метод элементарных превращений).
Для данной матрицы -го порядка строится прямоугольная матрица размера , к которой применяется преобразование по алгоритму полного исключения, в результате чего матрица сводится к виду , где . Это всегда возможно, если матрица невырожденная.
Обобщим знания о системах уравнений с помощью таблицы 1.1.
Понятия Или соотношенияФормулаОбщая система линейных алгебраических уравненийОсновная матрица системыМатрица-столбец свободных членовМатрица-столбец неизвестныхМатричная форма записи системыРасширенная матрица системыУсловие совместимости системыСистема имеет единственное решениеСистема имеет бесконечное множество решенийСистема несовместнаяКвадратная система линейных алгебраических уравненийКвадратная система имеет единственное решениеКвадратная система бесконечное множество решений, Квадратна система несовместная, Однородная система уравненийОднородная система имеет только нулевое решениеОднородная система имеет нетривиальные решенияКвадратная однородная система имеет только нулевое решениеКвадратная однородная система имеет нетривиальные решенияСтруктура общего решения однородной системы,
— произвольные числа; , — число неизвестных. Структура общего решения неоднородной системы,
где — некоторое частное решение неоднородной системы, — общее решение соответствующей однородной системы.
1.4 Ответы на теоретические вопросы
1. Теорема Кронекера-Капелли: для совместности системы необходимо и достаточно, чтобы ранг матрицы этой системы был равен рангу ее расширенной матрицы
2. Система имеет единственное решение, если ранг матрицы этой системы был равен рангу ее расширенной матрицы и равен количеству неизвестных системы.
3. Система имеет бесконечное множество решений, если ранг матрицы меньше количества неизвестных системы.
. Свободные переменные — те переменные, которые задаются произвольными значениями, а базисные переменные — те, которые выражаются через свободные.
5. Количество базисных переменных равняется рангу матрицы системы.
. Если ранг матрицы равен r, а количество неизвестных равняется n, то система может иметь (n-r) свободных переменных.
. Система называется однородной, если она имеет вид: АХ=0, т.е. все свободные члены равны нулю.
. Решение называется ненулевым, если все переменные одновременно не принимают значение 0.
. Для того, чтобы однородная система имела только тривиальное решение, необходимо и достаточно, чтобы ранг матрицы равнялся количеству неизвестных системы.
. Для того, чтобы однородная система имела нетривиальные решения, необходимо и достаточно, чтобы ранг матрицы был меньше количества неизвестных системы.
. Максимальное число линейно независимых решений однородной системы называется фундаментальной системой решений.
. Однородная система уравнений имеет фундаментальную систему решений, если ранг матрицы системы не равен количеству переменных системы.
. Фундаментальная система решений однородной системы содержит (n-r) решений, где n — число неизвестных системы, r-ранг матрицы системы.
. Однородная система уравнений может иметь от 0 до (n-1) фундаментальных систем решений, где n — число неизвестных системы.
. Если свободным переменным поочередно придавать значения: 1, 0,0…0; 0, 1, 0…0; …; 0, 0, …, 1, то полученная фундаментальная система решений называется нормированной.
Kypсовая работа посодействовала более углубленному изучению курса «Алгебра и геометрия», осмыслению его и применению для решения задач практического содержания.
Данная работа раскрыла вопрос решения систем уравнений, а также определила, как на практике использовать знания из курса «Алгебра и геометрия» для решения задач различного типа.
В теоретической части были полностью раскрыты значения тех понятий, которые приводились во вступлении, а именно система линейных уравнений, общее и частное решения, совместность и несовместность систем, однородные и неоднородные системы, рассмотрены различные методы решения систем уравнений. Также даны ответы на теоретические вопросы.
В практической части были решены все поставленные задачи, а именно: решены предложенные системы, выполнена проверка, решены экономические задачи, сводящиеся к системам уравнений.
1. Апатенок Р.Ф. и др. Элементы линейной алгебры и аналитической геометрии. — Минск: Вышейш. шк., 1986. — 272 с.
2. Тевяшев А.Д., Литвин О.Г. Алгебра і геометрiя: Лiнiйна алгебра. Аналітична геометрія: — Харків: ХТУРЕ, 2000. — 388 с.
. Данко П.Е. и др. Высшая математика в упражнениях и задачах. Ч.I. — М.: Высш. шк., 1986. — 304 с.
. Апатенок Р.Ф. и др. Сборник задач по линейной алгебре и аналитической геометрии. — Минск. Вышейш. шк., 1990. — 286 с.
. Тевяшев А.Д., Литвин О.Г. Вища математика. Загальний курс: Збiрник задач та вправ. — Х.: Рубiкон, 1999. — 320 с.
. Барковский В.В., Барковская Н.В. Математика для экономистов. Высшая математика. — К.: Национальная академия управления, 1999. — 399 с.
Теги: Системы линейных уравнений Курсовая работа (теория) Математика
http://www.bestreferat.ru/referat-110473.html
http://dodiplom.ru/ready/129405

 , является основной оценкой качества метода. По этому числу проводится сравнение различных методов.
, является основной оценкой качества метода. По этому числу проводится сравнение различных методов. (2) i=1, 2,…, m, где
(2) i=1, 2,…, m, где  ,
,  , при этом aii
, при этом aii 0.
0. (3). В методе Якоби исходят из записи системы в виде (2), итерации при этом определяют следующим образом:
(3). В методе Якоби исходят из записи системы в виде (2), итерации при этом определяют следующим образом:  , (n=0, 1, …, n0, i=1, 2, …, m) (4).
, (n=0, 1, …, n0, i=1, 2, …, m) (4). – (i=0, 1, …, m ) задаются произвольно (в программе мы это проделываем, вводя функцию по генерации случайных чисел – «random»). Окончание итерационного процесса определяют либо заданием максимального числа итераций n0 , либо следующим условием:
– (i=0, 1, …, m ) задаются произвольно (в программе мы это проделываем, вводя функцию по генерации случайных чисел – «random»). Окончание итерационного процесса определяют либо заданием максимального числа итераций n0 , либо следующим условием:  , где
, где  .
. ,
,  , то этот предел является решением системы (2).
, то этот предел является решением системы (2). , i=1, 2, …, m.
, i=1, 2, …, m. (i = 1, 2, …n ) (5). Выбираются произвольно начальные приближения корней x1 (0) , x2 (0) ,…, x n (0) , чтобы они в какой-то мере соответствовали неизвестным x1 , x2 , x3 ,…, xn .
(i = 1, 2, …n ) (5). Выбираются произвольно начальные приближения корней x1 (0) , x2 (0) ,…, x n (0) , чтобы они в какой-то мере соответствовали неизвестным x1 , x2 , x3 ,…, xn . корней известно, тогда в соответствии с идеей метода строится (k +1) – е приближение по следующим формулам:
корней известно, тогда в соответствии с идеей метода строится (k +1) – е приближение по следующим формулам: