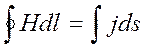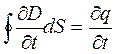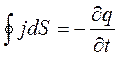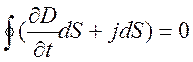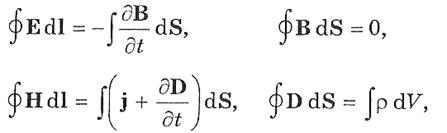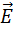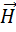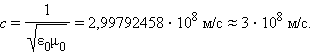Уравнения Максвелла. Электромагнитные волны
2. Система уравнений Максвелла
3. ЭМ волны и их характеристики
4. Получение ЭМ волн – опыты Герца
5. Применение ЭМ волн
1. В реальной жизни не существует отдельно электрического и магнитного полей, есть единое электромагнитное поле.
Теория электромагнитного поля, начала которой заложил Фарадей, математически была завершена Максвеллом. Важной выдвинутой Максвеллом идеей, была мысль о симметрии во взаимозависимости электрического и магнитного полей. А именно, поскольку меняющееся во времени магнитное поле (dB/dt) создает электрическое поле, следует ожидать, что меняющееся во времени электрическое поле (dE/dt) создает магнитное поле.
Согласно теореме о циркуляции вектора Н
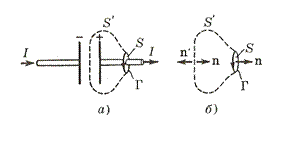
В качестве контура Г возьмем кривую, охватывающую провод. На контур Г можно натянуть разные поверхности, например S и S’. Обе поверхности имеют «равные права», однако через поверхность S течет ток I, а через поверхность S’ нет тока. Поверхность S’ «пронизывает» только электрическое поле. По теореме Гаусса поток вектора D сквозь замкнутую поверхность
Согласно определения плотности тока имеем
Сложим левые и правые части уравнений, получим
Из уравнения видно, что кроме плотности тока проводимости j имеется еще одно слагаемое dD/dt,размерность которого равна размерности плотности тока.
Максвелл назвал это слагаемое плотностью тока смещения:
Сумму же тока проводимости и тока смещения называют полным током.
Линии полного тока являются непрерывными в отличие от линий тока проводимости. Токи проводимости, если они не замкнуты, замыкаются токами смещения.
Следует иметь в виду, что ток смещения эквивалентен току проводимости только в отношении способности создавать магнитное поле.
Токи смещения существуют лишь там, где меняется со временем электрическое поле. В сущности он сам является переменным электрическим полем.
Открытие Максвеллом тока смещения — чисто теоретическое открытие, причем первостепенной важности.
2. С введением тока смещения макроскопическая теория электромагнитного поля была завершена. Открытие тока смещения (dD/dt) позволило Максвеллу создать единую теорию электрических и магнитных явлений. Теория Максвелла не только объяснила все разрозненные явления электричества и магнетизма, но и предсказала ряд новых явлений, существование которых подтвердилось впоследствии.
В основе электромагнитной теории Максвелла лежат четыре фундаментальных уравнений электродинамики, называемые уравнениями Максвелла.
Эти уравнения в сжатой форме выражают всю совокупность наших сведений об электромагнитном поле.
Содержание этих уравнений заключается в следующем:
1. Циркуляция вектора Е по любому замкнутому контуру равна со знаком минус производной по времени от магнитного потока через любую поверхность, ограниченную данным контуром. При этом под Е понимается не только вихревое электрическое поле, но и электростатическое.
2. Поток вектора В сквозь произвольную замкнутую поверхность всегда равен нулю.
3. Циркуляция вектора Н по любому замкнутому контуру равна полному току (току проводимости и току смещения) через произвольную поверхность, ограниченную данным контуром.
4. Поток вектора D сквозь любую замкнутую поверхность равен алгебраической сумме сторонних зарядов, охватываемых этой поверхностью.
Из уравнений Максвелла для циркуляции векторов Е и Н следует, что электрическое и магнитное поля нельзя рассматривать как независимые: изменение во времени одного из этих полей приводит к появлению другого. Поэтому имеет смысл лишь совокупность этих полей, описывающая единое электромагнитное поле.
Эти уравнения говорят о том, что электрическое поле может возникнуть по двум причинам. Во-первых, его источником являются электрические заряды, как сторонние, так и связанные. Во-вторых, поле Е образуется всегда, когда меняется во времени магнитное поле.
Эти же уравнения говорят о том, что магнитное поле В может возбуждаться либо движущимися электрическими зарядами (электрическими токами), либо переменными электрическими полями, либо тем и другим одновременно. Никаких источников магнитного поля, подобных электрическим зарядам, в природе не существует, это следует из второго уравнения.
Значение уравнений Максвелла не только в том, что они выражают основные законы электромагнитного поля, но и в том, что путем их решения (интегрирования) могут быть найдены сами поля Е и В.
Уравнения Максвелла обладают большей общностью, они справедливы и в тех случаях, когда существуют поверхности разрыва — поверхности, на которых свойства среды или полей меняются скачкообразно.
Фундаментальные уравнения Максвелла еще не составляют полной системы уравнений электромагнитного поля. Этих уравнений недостаточно для нахождения полей по заданным распределениям зарядов и токов. Их необходимо дополнить соотношениями, эти соотношения называют материальными уравнениями.
Материальные уравнения наиболее просты в случае достаточно слабых электромагнитных полей, сравнительно медленно меняющихся в пространстве и во времени. В этом случае для изотропных сред, материальные уравнения имеют следующий вид:
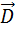
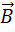
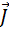
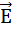
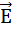
Уравнения Максвелла обладают рядом свойств.
1 свойства – линейности.
Уравнения Максвелла линейны, т.к. они содержат только первые производные полей Е и В по времени и пространственным координатам и первые степени плотности электрических зарядов и токов.
Свойство линейности уравнений Максвелла непосредственно связано с принципом суперпозиции: если два каких-нибудь поля удовлетворяют уравнениям Максвелла, то это относится и к сумме этих полей.
2 свойство – непрерывности.
Уравнения Максвелла содержат уравнение непрерывности, выражающее закон сохранения электрического заряда.
3 свойство – инвариантности.
Уравнения Максвелла выполняются во всех инерциальных системах отсчета. Они являются релятивистски инвариантными. Это есть следствие принципа относительности, согласно которому все инерциальные системы отсчета физически эквивалентны друг другу. Факт инвариантности уравнений Максвелла подтверждается многочисленными опытными данными.
Уравнения Максвелла являются правильными релятивистскими уравнениями в отличие, например, от уравнений механики Ньютона.
4 свойство – симметрии.
Уравнения Максвелла не симметричны относительно электрического и магнитного полей. Это обусловлено тем, что в природе существуют электрические заряды, но нет зарядов магнитных.
В нейтральной однородной непроводящей среде уравнения Максвелла приобретают симметричный вид.
Из уравнений Максвелла следует вывод о существовании принципиально нового физического явления: электромагнитное поле способно существовать самостоятельно — без электрических зарядов и токов. При этом изменение его состояния обязательно имеет волновой характер. Поля такого рода называют электромагнитными волнами.В вакууме они всегда распространяются со скоростью, равной скорости с.
Выяснилось также, что ток смещения (dD/dt) играет в этом явлении первостепенную роль. Именно его присутствие наряду с величиной dB/dt и означает возможность появления электромагнитных волн. Всякое изменение во времени магнитного поля возбуждает поле электрическое, изменение же поля электрического, в свою очередь, возбуждает магнитное поле.
За счет непрерывного взаимопревращения или взаимодействия они и должны сохраняться — электромагнитное возмущение будет распространяться в пространстве.
Теория Максвелла не только предсказала возможность существования электромагнитных волн, но и позволила установить все их основные свойства.
3. Существование электромагнитных волн было теоретически предсказано великим английским физиком Дж. Максвеллом в 1864 году.
Гипотеза Максвелла была лишь теоретическим предположением, не имеющим экспериментального подтверждения, однако на ее основе Максвеллу удалось записать непротиворечивую систему уравнений, описывающих взаимные превращения электрического и магнитного полей, то есть систему уравнений электромагнитного поля (уравнений Максвелла). Из теории Максвелла вытекает ряд важных выводов, одним из них явился вывод о существовании электромагнитных волн.
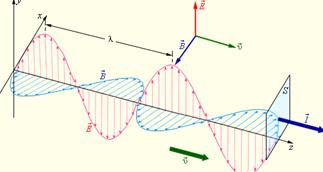
Электромагнитные волны поперечны – векторы 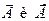
Электромагнитные волны распространяются в веществе с конечной скоростью
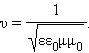
где ε и μ – диэлектрическая и магнитная проницаемости вещества, ε0 и μ0 – электрическая и магнитная постоянные.
Скорость электромагнитных волн в вакууме (ε = μ = 1):
Скорость c распространения электромагнитных волн в вакууме является одной из фундаментальных физических постоянных.
4. Максвелл утверждал, что электромагнитные волны обладают свойствами отражения, преломления, дифракции и т.д. Но любая теория становится доказанной лишь после ее подтверждения на практике. Но в то время ни сам Максвелл, ни кто-либо другой еще не умели экспериментально получать электромагнитные волны. Это произошло только после 1888 года, когда Герц экспериментально открыл электромагнитные волны.
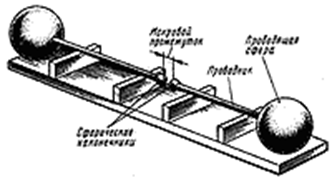
Сферы подсоединялись ко вторичной обмотке катушки Румкорфа, являвшейся источником высокого напряжения.
Из теории Максвелла известно,
1)излучать электромагнитную волну может только ускоренно движущийся заряд,
2)что энергия электромагнитной волны пропорциональна четвертой степени ее частоты.
Понятно, что ускоренно заряды движутся в колебательном контуре, поэтому проще всего их использовать для излучения электромагнитных волн. Но надо сделать так чтобы частота колебаний зарядов стала как можно выше. Из формулы Томсона для циклической частоты колебаний в контуре 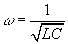
Суть происходящих в вибраторе явлений заключается в следующем. Индуктор Румкорфа создает на концах своей вторичной обмотки очень высокое, порядка десятков киловольт, напряжение, заряжающее сферы зарядами противоположных знаков. В определенный момент в искровом промежутке вибратора возникает электрическая искра, делающая сопротивление его воздушного промежутка столь малым, что в вибраторе возникают высокочастотные затухающие колебания, длящиеся во все время существования искры. Поскольку вибратор представляет собой открытый колебательный контур, происходит излучение электромагнитных волн.
После огромной серии трудоемких и чрезвычайно остроумно поставленных опытов с использованием простейших, так сказать, подручных средств экспериментатор достиг цели. Удалось измерить длины волн и рассчитать скорость их распространения. Были доказаны
- интерференции и поляризации волн.
- измерена скорость электромагнитной волны
5. Впервые электромагнитные волны были использованы через семь лет после опытов Герца. 7 мая 1895 г. преподаватель физики офицерских минных классов А. С. Попов (1859—1906) на заседании Русского физико-химического общества продемонстрировал первый в мире радиоприемник, открывший возможность практического использования электромагнитных волн для беспроволочной связи, преобразившей жизнь человечества. Первая переданная в мире радиограмма содержала лишь два слова: «Генрих Герц». Изобретение радио Поповым сыграло огромную роль для распространения и развития теории Максвелла.
Электромагнитные волны сантиметрового и миллиметрового диапазонов, встречая на своем пути преграды, отражаются от них. Это явление лежит в основе радиолокации — обнаружения предметов (например, самолетов, кораблей и т. д.) на больших расстояниях и точного определения их положения. Помимо этого, методы радиолокации используются для наблюдения прохождения и образования облаков, движения метеоритов в верхних слоях атмосферы и т. д.
Для электромагнитных волн характерно явление дифракции — огибание волнами различных препятствий. Именно благодаря дифракции радиоволн возможна устойчивая радиосвязь между удаленными пунктами, разделенными между собой выпуклостью Земли. Длинные волны (сотни и тысячи метров) применяются в фототелеграфии, короткие волны (несколько метров и меньше) применяются в телевидении для передачи изображений на небольшие расстояния (немногим больше пределов прямой видимости). Электромагнитные волны используются также в радио-геодезии для очень точного определения расстояний с помощью радиосигналов, в радиоастрономии для исследования радиоизлучения небесных тел и т. д. Полное описание применения электромагнитных волн дать практически невозможно, так как нет областей науки и техники, где бы они не использовались.
Для осуществления радио- и телевизионной связи используются электромагнитные волны с частотой от нескольких сотен тысяч герц до сотен мегагерц.
При передаче по радио речи, музыки и других звуковых сигналов применяют различные виды модуляции высокочастотных (несущих) колебаний. Суть модуляции заключается в том, что высокочастотные колебания, вырабатываемые генератором, изменяют по закону низкой частоты. В этом и заключается один из принципов радиопередачи. Другим принципом является обратный процесс — детектирование. При радиоприеме из принятого антенной приемника модулированного сигнала нужно отфильтровать звуковые низкочастотные колебания.
С помощью радиоволн осуществляется передача на расстояние не только звуковых сигналов, но и изображения предметов.
Уравнения Максвелла
Вы будете перенаправлены на Автор24
Значение уравнений Максвелла
Уравнения Дж. Максвелла создают основу для предложенной им теории электромагнитных явлений, которая объяснила все известные в то время эмпирические факты, некоторые эффекты предсказала. Главным выводом теории Максвелла стало положение о существовании электромагнитных волн, которые распространяются со скоростью света.
Уравнения, предложенные Максвеллом, в электромагнетизме играют роль подобную роли законов Ньютона в классической механике. Они явились обобщением экспериментальных законов и продолжением идей ученых (Кулона, Ампера, Фарадея и др.) изучавших электромагнетизм до Максвелла.
Сам Максвелл предложил двадцать уравнений в дифференциальной форме с двадцатью неизвестными величинами. В современном виде мы имеем систему уравнений Максвелла благодаря немецкому физику Г. Герцу и англичанину О. Хэвисайду. С помощью этих уравнений можно описать все электромагнитные явления.
Система уравнений Максвелла
Систему уравнений Максвелла составляют:
Выражения (1)-(4) называют полевыми уравнениями, они применимы для описания всех макроскопических электромагнитных явлений. Иногда уравнения системы Максвелла группируют в пары, первую пару составляют из второго и третьего уравнения, вторую пару — из первого и четвертого уравнений. При этом говорят, что в первую пару уравнений входят только основные характеристики поля ($\overrightarrow
Каждое из векторных уравнений (1) и (2) эквивалентно трем скалярным уравнениям. Эти уравнения связывают компоненты векторов, которые находятся в левой и правой частях выражений. Так, в скалярном виде уравнение (1) представляется как:
Готовые работы на аналогичную тему
В скалярном виде уравнение (2) запишем как:
Третье уравнение из системы Максвелла в скалярном виде:
Четвертое уравнение в скалярной форме примет следующий вид:
Для того чтобы рассмотреть конкретную ситуацию, систему уравнений (1)-(4) дополняют следующими материальными уравнениями, которые учитывают электромагнитные свойства среды:
Необходимо отметить, что существует целый ряд явлений, в которых материальные уравнения существенно отличны от уравнений (5), например, если речь идет о нелинейных явлениях. В таких случаях получение материальных уравнений составляет отдельную научную задачу.
Физический смысл уравнений Максвелла
Уравнение (1) системы указывает на то, что двумя возможными источниками магнитного поля являются токи проводимости ($\overrightarrow
Уравнение (2) является законом электромагнитной индукции и отображает тот факт, что переменное магнитное поле — один из источников возникновения электрического поля.
Следующим источником электрического поля служат электрические заряды, что и отображает уравнение (4), которое является, по сути, законом Кулона.
Уравнение (3) означает, что линии магнитной индукции не имеют источников (они либо замкнуты, либо уходят в бесконечность), что приводит к выводу об отсутствии магнитных зарядов, которые создают магнитное поле.
Материальные уравнения (5) — это соотношения между векторами поля и токами. Диэлектрические свойства среды заключены в диэлектрической проницаемости ($\varepsilon $). Магнитные свойства, которые описывает намагниченность, учтены в магнитной проницаемости ($\mu $). Проводящие свойства среды сосредоточены в удельной проводимости ($\sigma $).
Уравнения поля линейны и учитывают принцип суперпозиции.
Границы применимости уравнений Максвелла
Система уравнений Максвелла ограничена следующими условиями:
Материальные тела должны быть неподвижны в поле.
Постоянные $\varepsilon ,\ \mu ,\sigma $ могут зависеть от координат, но не должны зависеть от времени и векторов поля.
В поле не должно находиться постоянных магнитов и ферромагнитных тел.
Если существует необходимость учета движения среды, то уравнения системы Максвелла оставляют неизменными, а движение учитывается в материальных уравнениях, которые становятся зависимыми от скорости среды и существенно усложняются. Кроме прочего материальные уравнения перестают быть соотношениями между парами величин, как в (5). Например, плотность тока проводимости становится зависимой от индукции магнитного поля, а не только от напряженности электрического поля.
Магнитное поле постоянных магнитов, например, можно описать, используя систему Максвелла, если известна намагниченность. Но, если заданы токи, то в присутствии ферромагнетиков описать поле при помощи данных уравнений не получится.
Задание: Докажите, что из уравнений Максвелла следует закон сохранения заряда.
Решение:
В качестве основания для решения задачи используем из системы Максвелла уравнение:
Проведем операцию дивергирования в обеих частях выражения (1.1):
Для выражения (1.2) в соответствии с теоремой равенстве нулю дивергенции ротора имеем:
Рассмотрим второе слагаемое в правой части. Мы можем поменять порядок дифференцирования, так как время и пространственные координаты независимы, то есть записать:
В соответствии с системой Максвелла мы знаем, что источниками электрических полей служат заряды или:
Что позволяет нам записать уравнение (1.4) в виде:
Что дает нам закон сохранения заряда, который записан в виде:
Данное уравнение называют уравнением непрерывности тока, оно содержит в себе закон сохранения заряда, что совершенно очевидно, если выражение (1.8), записать в интегральной форме:
тогда если области замкнуты и изолированы получаем:
Что требовалось доказать.
Задание: Покажите, что уравнения $rot\overrightarrow
Решение:
За основу решения примем уравнение:
Возьмём дивергенцию от обеих частей уравнения:
В соответствии с теоремой равенстве нулю дивергенции ротора имеем:
Соответственно, получаем, что
Выражение $div\overrightarrow=const$ не противоречит тому, что $div\overrightarrow=0$.
Мы получили, что уравнения $rot\overrightarrow
Получи деньги за свои студенческие работы
Курсовые, рефераты или другие работы
Автор этой статьи Дата последнего обновления статьи: 01 03 2021
Из уравнений максвелла следует вывод о существовании
Основные уравнения классической электродинамики (система уравнений Максвелла) по праву являются общепризнанными уравнениями и широко применяются в физике, радиофизике и электронике. Однако эти уравнения не были получены из общих физических законов, что не позволяло считать их абсолютно точными, допускало различного рода манипуляции с ними. Тем не менее, эти уравнения точные и выводятся из общих принципов физики и основ векторной алгебры [1, 2].
1. Вывод закона электромагнитной индукции Фарадея
Закон электромагнитной индукции Фарадея можно получить из уравнения для электромагнитных сил, действующих на точечный электрический заряд [1, 2]:
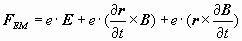 , , | (1) |
где e – заряд электрона, E – вектор напряженности электрического поля, r – радиальный вектор, соединяющий ось источника магнитной индукции B с электрически заряженной частицей и лежащий в плоскости, ортогональной оси симметрии магнитного поля.
Рассмотрим случай, когда магнитная часть силы FЕМ равна и направлена противоположно ее электрической части:
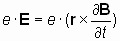 . . | (2) |
Такая ситуация возникает в проводнике с электрическим током высокой частоты, когда сила, действующая на электрон со стороны первичного электрического поля изменяется настолько быстро, что оказывается в противофазе с силой инерции электронов.
Сократим заряд в равенстве (2) и применим к обеим частям этого равенства операцию «ротор»:
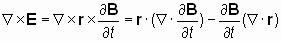 . . | (3) |
Пусть, например, ось z совпадает с направлением аксиального вектора B, тогда радиус-вектор будет иметь вид: r=xi+yj, где i и j – единичные векторы в направлениях осей координат x и y, соответственно. Радиальный векторr не имеет третьей составляющей вдоль оси z, поэтому второе слагаемое в (3) равно –2(∂B/∂t). Первое же слагаемое в уравнении (3) равно ∂B/∂t. В результате, после преобразования правой части последнего равенства, получаем:
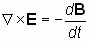 . . | (4) |
То есть из электромагнитного силового уравнения (1) в том случае, когда сила, действующая на электрон со стороны магнитного поля, полностью уравновешивается силой со стороны электрического поля, следует закон электромагнитной индукции Фарадея (4), − одно из основных уравнений электродинамики.
Уравнения (2) – (4) не зависят от того, имеется или отсутствует электрон в данной точке пространства. В результате такой независимости электрического и магнитного полей от электрического заряда уравнение (4) отражает пространственно-временные свойства самих изменяющихся полей, представимых в виде единого электромагнитного поля. При этом закон Фарадея (4) не только представляет собой закон электромагнитной индукции, но является и основным законом взаимного преобразования электрического и магнитного полей, − неотъемлемым свойством электромагнитного поля.
2. Вывод уравнения Максвелла
Прежде, чем приступить к выводу уравнения Максвелла, необходимо дополнить векторную алгебру еще одним векторным оператором.
2.1. Определение векторного оператора, выполняющего действие, обратное векторному преобразованию дифференциального векторного оператора «ротор»
Дифференциальный векторный оператор «ротор» выполняет операцию преобразования векторов в пространстве и операцию дифференцирования, то есть является сложным оператором, осуществляющим сразу два вида действий. Это прямо следует из его определения [3]:
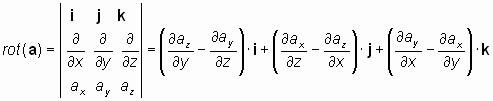
где а – вектор, i, j, k – единичные векторы в направлении осей прямоугольной (декартовой) системы координат x, y и z, соответственно. При этом оператор, обратный оператору «ротор», в векторном анализе не определен, хотя каждое из выполняемых им преобразований, в принципе, обратимо.
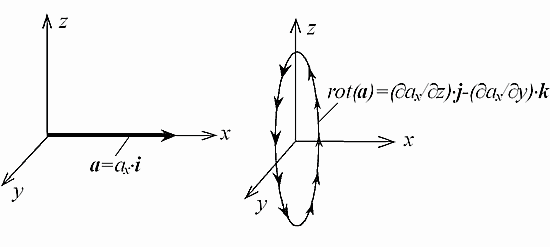
Геометрическая иллюстрация пространственного преобразования вектора а в вектор rot(a), осуществляемая оператором «ротор», показана на Рис. 1.
Рис. 1. Геометрическое представление вектора а и векторного поля, образованного оператором «ротор».
2.2. Определение 1. Если два взаимосвязанных векторных поля, представленные векторами а и b, имеют производные по пространственным переменным x, y, z (в виде rotaи rotb)и производные по времени, ¶ а/ ¶ t и ¶ b/ ¶ t, причем производная вектора а по времени ортогональна производным по пространственным переменным вектора b, и наоборот, производная по времени вектора b ортогональна производным по пространственным переменным вектораа, то существует векторный оператор, осуществляющий пространственное преобразование векторного поля, не затрагивающее операцию дифференцирования, который условно назовем оператором «rerot», (противоположно закрученный или «реверсивный ротор») такой, что:
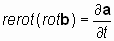
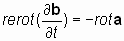
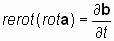
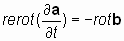
2.3. Свойства векторного оператора «реверсивный ротор»
2.3.1. Векторный оператор «реверсивный ротор» действует только на производные вектора.
2.3.2. Векторный оператор «реверсивный ротор» располагается перед производной вектора, на которую он действует.
2.3.3. Константы и числовые коэффициенты при производных вектора могут быть вынесены за пределы действия векторных операторов:
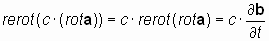

2.3.4. Векторный оператор «реверсивный ротор» действует на каждое из слагаемых уравнения, содержащего сумму векторных производных:
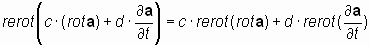
2.3.5. Результат действия векторного оператора «реверсивный ротор» на ноль есть ноль:
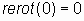
При этом результат действия векторного оператора «реверсивный ротор» на другие константы, в том числе на вектор, согласно пункту 2.3.1, не определен.
2.4. Пример применения оператора «реверсивный ротор»
Применим оператор «реверсивный ротор» к уравнению, содержащему взаимосвязанные векторы a и b:
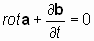 . . | ((*)) |
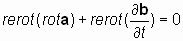
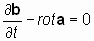 . . | ((**)) |
Если теперь еще раз применить оператор «реверсивный ротор» к вновь образованному равенству (**), то получим:

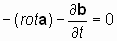
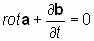 . . | ((*)) |
Последовательное двойное (или любое четное) применение оператора «реверсивный ротор» приводит к исходному равенству. Этим самым векторный оператор «реверсивный ротор» осуществляет не только взаимное преобразование дифференциальных уравнений взаимосвязанных векторных полей, но и устанавливает эквивалентность этих уравнений.
Геометрически это выглядит так. Оператор «ротор» дифференцирует и как бы закручивает прямолинейное векторное поле, делая его вихревым и ортогональным исходному векторному полю. Векторный оператор «реверсивный ротор» выполняет векторное преобразование, которое как бы раскручивает вихревое поле, закрученное оператором «ротор», превращая его в изменяющееся невихревое поле, представленное производной вектора по времени. Поскольку интегрирование не производится, производная вектора по времени соответствует изменению величины вектора. В результате имеем изменение вектора, величина которого изменяется в единственном направлении, ортогональном пространственным переменным оператора «ротор». И наоборот, векторный оператор «реверсивный ротор» закручивает невихревое изменяющееся векторное поле, представленное производной вектора по времени, превращая его в вихревое пространственное векторное поле, ортогональное исходной производной вектора по времени. Так как направление «кручения» оператора «реверсивный ротор» противоположно направлению вращения, осуществляемому оператором «ротор», то знак вновь образованного вихревого поля выбирается противоположным (отрицательным). То есть векторный оператор «реверсивный ротор» выполняет действие, обратное пространственному преобразованию оператора «ротор» на всем «пространстве» производных векторных полей. В то же время векторный оператор «реверсивный ротор» сам не дифференцирует вектор, на производную которого он действует. Этим самым осуществляется тождественное обратимое векторное преобразование.
Если ввести в векторный анализ интегральный векторный оператор, восстанавливающий не производную вектора, а сам вектор из ротора вектора (условно назовем такой оператор обратным ротором, или «rot -1 »), то такой оператор наряду с обратным векторным преобразованием одновременно должен производить операцию интегрирования.
Однако, в силу неоднозначности математической операции интегрирования, полностью обратный «ротору» оператор rot -1 не осуществляет однозначное обратное векторное преобразование.
2.5. Применение векторного оператора «реверсивный ротор» к физическим полям
При применении векторного оператора «реверсивный ротор» к физическим векторным полям необходимо учитывать изменение размерности правой и левой частей уравнения из-за перестановки переменных x, y, z и t при преобразовании. Обозначим размерность координат – метр (L), а времени – секунда (T).
Определение 2. Для физических векторных полей векторный оператор «реверсивный ротор», определяется следующим образом:
и 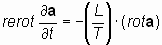 ; ; | (6) |
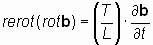
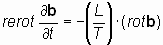
Обозначая размерное отношение L/T, как константу v, имеющую размерность скорости, [м/с], уравнения (6.4) и (6.4*) можно представить в виде:
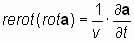 и и 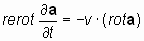 ; ; | (7) |
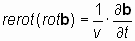 и и 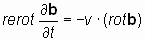 . . | (7*) |
2.6. Применение оператора «реверсивный ротор» к физическим полям
Применим векторный оператор «реверсивный ротор», определенный уравнениями (7), (7*), к уравнению (4), связывающему реальные физические поля E и B в электродинамике:
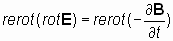

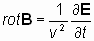 | (8) |
Электродинамическая постоянная «v» не зависит ни от величины полей, ни от скорости их изменения и, как следует из волнового уравнения, соответствует скорости распространения волны электромагнитного взаимодействия, c » 2.99792458 Ч 10 8 м/c, которая называется также скоростью света в вакууме.
То есть с помощью векторного преобразования «реверсивный ротор» из уравнения (4), представляющего собой закон электромагнитной индукции Фарадея, естественным образом вытекает одно из основных уравнений электродинамики — уравнение Максвелла (8), которое не следует ни из эксперимента, ни из известных физических законов. Уравнения (4) и (8) являются взаимосвязанными, трансформируемыми друг в друга при помощи векторного преобразования, что соответствует их физической эквивалентности. Поэтому справедливость одного из этих уравнений, установленная в виде физического закона (в данном случае — это закон электромагнитной индукции Фарадея (4)) является достаточным условием для утверждения о справедливости второго уравнения (уравнения Максвелла (8)) в качестве эквивалентного физического закона.
2.7. Трансформация векторных полей
Если исходить из определения оператора «ротор», то действие векторного оператора «обратный ротор», казалось бы, можно представить в виде, показанном на Рис. 2, где предполагается некоторая тождественность векторных полей до и после векторного преобразования дифференциальным векторным оператором «ротор».
Проверим это предположение. Применим оператор «реверсивный ротор» к уравнению:
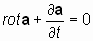
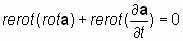

Полученное равенство изменяет направление векторов в исходном определении дифференциального векторного оператора «ротор», что недопустимо.
Поэтому 
Применение векторного оператора «реверсивный ротор» к производным одного и того же векторного поля показывает принципиальное различие между векторным полем до применения, и векторным полем после применения оператора «ротор». Это означает необходимость представлять поле вектора а и поле вектора rot(а) как трансформируемые друг в друга, но различные векторные поля.
Исходное векторное поле, представленное вектором а, будем считать первичным (причиной), а поле, образованное векторным преобразованием оператора «ротор», будем считать вторичным полем (следствием действия оператора «ротор») и обозначим его, как поле векторов b.
Рис. 2. Результат отождествления векторных полей до и после векторного преобразования «ротор». Направление полей не соответствует исходному определению оператора «ротор», показанному на Рис. 1, «правый винт» превращается в «левый винт».
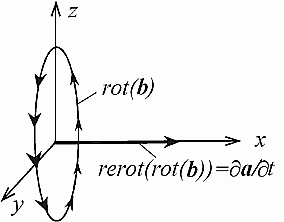
Тогда обратное преобразование векторных полей, не затрагивающее операции дифференцирования, во введенных таким образом обозначениях будет иметь вид, показанный на Рис. 3.
Рис. 3. Определение векторного преобразования, обратного операции «ротор», не затрагивающего операции дифференцирования. Разделение векторных полей выполнено по признаку причинно-следственных отношений. Исходное поле представлено вектором а (причина), а поле, образованное операцией «ротор», представлено вектором b (следствие).
В электродинамике в некоторых простейших случаях переход к вращающейся системе отсчета, внутри которой исчезает вращение, приводит к отсутствию сил со стороны магнитного поля, и силовое воздействие может быть представлено только силой со стороны электрического поля. Но из этого никак не следует вывод, что магнитного поля нет или оно всегда может быть заменено электрическим полем. Частный случай векторного поля, взятого в отдельной изолированной системе отсчета, относится только к данной выбранной системе, в которой осуществляется ограниченное по степеням свободы движение электрического заряда.
Поскольку в пространстве существуют и прямолинейные векторные поля, и вращающиеся замкнутые векторные поля, а находиться в двух системах отсчета одновременно невозможно, то в общем случае выбором системы координат нельзя свести одно поле к другому. Источник этих полей один – это электрические заряды. Электрические заряды создают вокруг себя электрическое поле (всесторонне направленное векторное поле), а движение электрических зарядов создает магнитное поле (замкнутое круговое векторное поле). При этом, естественно, прямолинейное движение электрических зарядов создает вокруг них круговое магнитное поле, а круговое движение электрических зарядов (равно как вращение электрически заряженных частиц вокруг собственной оси) создает прямолинейное в пространстве магнитное поле, заключенное в объеме, ограниченном радиусом вращения.
2.8. Скорость распространения электромагнитного взаимодействия
Скорость преобразования векторных полей друг в друга не зависит ни от величины полей, ни от скорости их изменения и, как следует из волнового уравнения, соответствует скорости распространения волны электромагнитного взаимодействия в свободном пространстве (вакууме),c » 2.99792458 Ч 10 8 м/c, и эта величина по праву называется электродинамической постоянной.
Таким образом, изменение электрического и магнитного полей, осуществляемое в трехмерном пространстве, имеет свойство взаимного преобразования векторов, и это свойство в электродинамике осуществляется посредством закона электромагнитной индукции Фарадея. Если считать такое преобразование прямым, то обратное преобразование векторных полей осуществляется при помощи уравнения, полученного Максвеллом интуитивным путем, и которое можно получить при помощи векторного оператора «реверсивный ротор». Взаимное преобразование электрического и магнитного полей, которое осуществляется без источников электрического заряда, представляет собой один из особых видов волнового движения — поперечную электромагнитную волну, которая переносит электромагнитную энергию в свободном пространстве с абсолютной скоростью преобразования полей. Но при этом источником энергии электромагнитной волны всегда являются ускоренно движущиеся электрические заряды.
3. Уравнения источников электромагнитных полей.
Оставшиеся два из четырех основных уравнений системы уравнений Максвелла лишь устанавливают факт наличия в природе электрических зарядов, создающих электрическое поле (теорема Гаусса, которая прямо следует из закона Кулона):
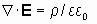
и факт отсутствия в природе магнитных зарядов:
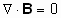
Литература
- Сокол-Кутыловский О.Л. Гравитационные и электромагнитные силы. Екатеринбург, 2005.
- Сокол-Кутыловский О.Л. Русская физика. Екатеринбург, 2006.
- Бронштейн И.Н., Семендяев К.А. Справочник по математике для инженеров и учащихся ВТУЗОВ (под редакцией Г. Гроше и В. Циглера), М., «Наука», 1980.
http://spravochnick.ru/fizika/uravneniya_maksvella/
http://www.trinitas.ru/rus/doc/0016/001b/00161290.htm