Из уравнений параметрически задающих функцию исключить параметр

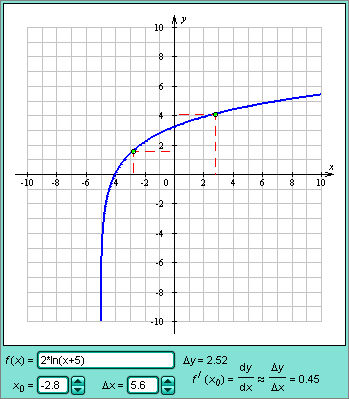
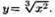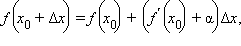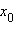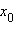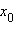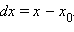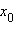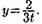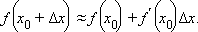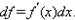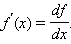Параметрическое задание функции

Вы будете перенаправлены на Автор24

Параметрический способ задания функций

Пусть даны два уравнения

$x=\phi (t)$ и $y=\psi (t)$

В которых $t$ принимает значения с отрезка [n1; n2]. Каждому значению t соответствуют значения x и y — координаты точки на плоскости Оxy.

Когда $t$ изменяет свое значение на промежутке от $n1$ до $n2$, точка описывает некоторую кривую. Уравнения $x=\phi (t)$ и $y=\psi (t)$ получили название параметрических для кривой, а $t$ — параметра.

Предположим, что функция $x=\phi (t)$ имеет обратную функцию $t=\ (x)$. Тогда справедливо равенство:

Параметрический способ задания функций широко применяется в механике. Так, если в плоскости некоторая материальная точка находится в движении (время $t$), и законы движения проекций этой точки на оси координат известны:

Уравнения являются параметрическими уравнениями траекторий движущейся точки. Исключая временной параметр, получим уравнение траектории в форме $y = f(x)$.

Определить траекторию и место падения груза, сброшенного с самолета, движущегося горизонтально со скорость $v_0$ на высоте $y_0$.

Допустим, что груз сбрасывается с момент пересечения самолетом оси Oy. Тогда очевидно, что горизонтальное перемещение груза равномерно и имеет постоянную скорость:

А вертикальное перемещение:

Следовательно, расстояние от груза до земли в произвольный момент падения:

Уравнения горизонтального и вертикального перемещения тела являются параметрическими. Для того, чтобы исключить временной параметр $t$, найдем его значение из первого уравнения.

Полученное выражение подставим во второе параметрическое уравнение чтобы найти уравнение траектории:

Готовые работы на аналогичную тему

Уравнения некоторых кривых в параметрической форме:

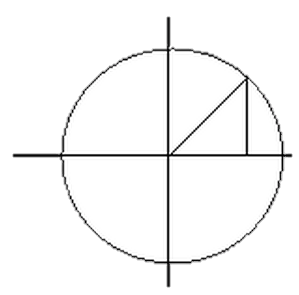
1. Окружность

Параметрические кривые окружности:

Рисунок 1. Окружность и ее параметрические кривые

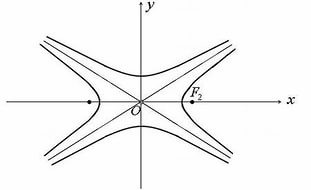
Уравнение гиперболы имеет вид:

Параметрические кривые гиперболы:

Рисунок 2. Гипербола и ее параметрические кривые

Записать уравнение окружности в параметрическом виде.

Представим уравнение окружности в виде: \[x^ <2>+y^ <2>=r^ <2>\] \[x^ <2>+y^ <2>=6^ <2>\]

Значит, радиус $r$ равен 6.

Записать уравнение гиперболы в параметрическом виде.

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 11 12 2021

Функции, заданные параметрически, и их дифференцирование

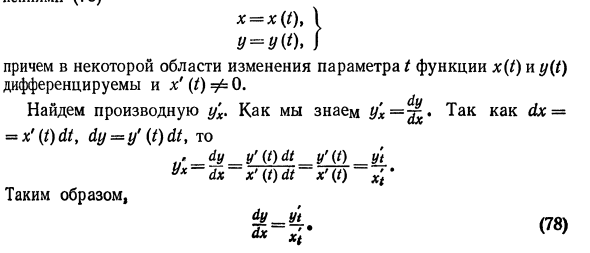
Функции, заданные параметрически, и их дифференцирование

• Функции, задаваемые параметрами и их отличиями /. Параметрические обязанности и линии До сих пор рассматривались линейные уравнения на плоскости, которые непосредственно связывают текущие координаты этих точек. Тем не менее, другой метод определения линий часто используется. В этом методе текущие координаты x и y считаются функцией третьей переменной. Укажите две функции переменной /. (73) То же значение / считается.

Когда переменная t проходит через все значения области функции (73), точка My) описывает конкретную линию C в плоскости Ohu. Уравнение (73) называется параметрическим уравнением этой линии, а переменная / называется параметром. Предположим, что функция x = x (() имеет обратную функцию / = φ (:) :).

Тогда одно из этих значений t соответствует однозначному значению x и однозначному значению y, так что определенная точка M (x \ y) соответствует. Людмила Фирмаль

Подставляя эту функцию во второе выражение (73), выражение (74) y = y [Φ (A ‘)], Выразите y как функцию от x. Я согласен, что эта функция параметрически определяется уравнением (73). Переход от этих уравнений к уравнению (74) называется исключением параметров. При рассмотрении функциональности, Найдите вторую производную. Второй по определению FX.

Dx2 рф * ‘дх Функция параметра- = / (/), DY \ дх) дх d ^

Следует рассматривать как заданную функцию Параметрический: 1 * = «(/). J ■ ‘8 Следовательно,

= определяется уравнением (78) вместо y ду Должен быть заменен (А ты (79) «» Dar Пример 3. Найти вторую производную функции y, определенной параметрически. x = sin2 /, ^ y = sin2 /. ) Решения. В примере 1 первая производная была найдена, но рассматривают эту производную как параметрически определенную функцию. | = 2ctg2 /, | я Пой- ^ 7.

Примеры решения и задачи с методическими указаниями

Согласно уравнению (78) * = найти sin2 /, вторая производная dyV ‘2 2 «в уравнении (79) Y /(2 ctg _ sin * 2 /__4dx2 «» * * (sin2 /) ‘

2 sin / cos / sin * 2 /’ \ Когда вы указываете параметр, исключение параметра не только не требуется, но и не всегда возможно на практике. Во многих случаях гораздо удобнее запрашивать разные значения для параметров и использовать уравнение (73) для вычисления соответствующих значений для аргументов x и y. Давайте посмотрим на некоторые примеры.

Пример 1.Декартовы координаты x и y этой точки выражаются полярным радиусом r-R и полярным углом. , §3, пункт 3): x = Rcostt \ y = Rs \ nt. ((7 ° Уравнение (75) называется параметрическим круговым уравнением. Эти параметры являются полярным углом / и варьируются от 0 до 2n. Если уравнение (75) возводится в квадрат и заканчивается для каждого члена, тождество устраняется тождеством cos2 // fsin2 / = 1, а круговое уравнение в декартовой системе координат xx + y2z = R * f определяет две основные функции вы: И tj- * / R2-A2’2. Каждая из этих функций определяется параметрически уравнением (75), но диапазон изменения параметров для этих функций различен.

Пусть M — любая точка на окружности с центром в начале координат и радиусе R. Людмила Фирмаль

Их первый 0 я Кроме того, в конкретной области изменения параметра t функции x (t) и y (t) дифференцируемы и x ‘(/) Φ0. Найдите производную y’x. Как вы знаете, yx = ^ 6 * dx = = x ‘(t) dt, dy = y’ (t) dt, то > dy_y ‘(t) dt y’ (t) yt yx dx x ‘

Пример 1. Найти производную функции y от k, заданную параметрическим уравнением x = sin2 /, \ y = sin2 /. Решение. Из уравнения (78) dy_y’t _ (sin 2Q ‘_ 2cos21 0 0 dx to x; (sin54 /)’ 2 sin / cos / ^ 8 Пример 2. Найти касательные и циклоидальные нормальные уравнения (А = 1) x = / -sin ^ r / = 1-cos / / T

Y ‘решение в точке Ml (xr; yx), соответствующей значению параметра. Найти координаты контакта Mt (xx \ yv). т. , Зло зла зло. Зло | -2 *! = (/ -Sin /) / = zy = -2 — Sin-2- = -2- + 1 * зло yt = (\ -cos /) = 1 — COS— = 1. • г Найти производную от уравнения (78), чтобы найти коэффициенты тангенса и нормального угла. dy_ (1-cos /) ‘_ sin t dx

Найти угловой коэффициент касательной к циклоиде в точке М. b-dJ-1- (sin / \ = —I * kas-

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Функция, заданная параметрически

Пусть зависимость между аргументом х и функцией у задана параметрически в виде двух уравнений

где t — вспомогательная переменная, называемая параметром.

Найдем производную у’_х, считая, что функции (21.1) имеют производные и что функция х=x(t) имеет обратную t=φ(х). По правилу дифференцирования обратной функции

Функцию у=ƒ(х), определяемую параметрическими уравнениями (21.1), можно рассматривать как сложную функцию у=y(t), где t=φ(х). По правилу дифференцирования сложной функции имеем: у’_х=y’_t•t’_x. С учетом равенства (21.2) получаем

Полученная формула позволяет находить производную у’_х от функции заданной параметрически, не находя непосредственной зависимости у от х.

2 , y’_t=2t. Следовательно, у’_х=2t/t 2 , т. е.

В этом можно убедиться, найдя непосредственно зависимость у от х.

Действительно, Тогда Отсюда т. е.

30) Дифференциал функции

Итак, график дифференцируемой функции в окрестности каждой своей точки сколь угодно близко приближается к графику касательной в силу равенства: где α – бесконечно малая в окрестности функция. Для приближенного вычисления значения функции f в точке x₀ + Δx эту бесконечно малую функцию можно отбросить:

Линейную функцию называют дифференциалом функции f в точке и обозначают df. Для функции x производная в каждой точке равна 1, то есть Поэтому пишут:

Приближенное значение функции вблизи точки равно сумме ее значения в этой точке и дифференциала в этой же точке. Это дает возможность записать производную следующим образом:

Часто эту запись используют, чтобы уточнить, по какой переменной дифференцируется функция.

31) Исследование функции при помощи первой производной

Под интервалом мы будем подразумевать или конечный интервал , или один из

следующих числовых промежутков: , или . Заметьте, что внутри

интервала нет выколотых точек. Таким образом, если , то .

Определение 1.1. Говорят, что функция строго монотонно возрастает в интервале ,

если при всех таких, что , т.е. бóльшим значениям

независимой переменной соответствуют бóльшие значения функции. Далее, строго

монотонно убывает в , если при .

В дальнейшем, говоря, что возрастает (или убывает) на , мы будем иметь в виду

возрастание (убывание) в строго монотонном смысле.

Теорема 1.2 (признак возрастания функции). Дифференцируемая функция

возрастает в интервале , если для всех .

Доказательство: Пусть и — любые две точки в такие, что . Надо

доказать, что . По теореме Лагранжа, примененной к функции на отрезке

, существует точка такая, что ,

откуда , потому что и . ■

Теорема 1.3 (признак убывания функции). Дифференцируемая функция убывает в

интервале , если для всех .

Доказательство: Аналогично доказательству предыдущей теоремы. ■

Пример 1.4. Определить промежутки возрастания и убывания функции

Рис. 1. Диаграмма возрастания и убывания функции .2

Решение: . Исследование представлено

диаграммой на рис. 1, где плюсы и минусы означают знаки производной, а стрелки —

возрастание или убывание данной функции на соответствующих интервалах. ■

Следствие 1.5 (признаки максимума и минимума в терминах первой производной).

Пусть — критическая точка дифференцируемой функции , т.е. .

а) Если меняет знак в точке с плюса на минус, то — локальный

б) Если меняет знак в точке с минуса на плюс, то — локальный

в) Если не меняет знак в точке , то локального экстремума в точке не

Пример 1.6. Найти локальные экстремумы функции из примера 1.4.

Решение: В силу предыдущей теоремы, из диаграммы на рис. 1 видно, что значения

и являются локальными минимумами, а локальным