Изображение свертки использование при решении уравнений

Примеры решений задач по операционному исчислению (преобразованию Лапласа)

Операционное (символическое) исчисление – это один из методов математического анализа, позволяющий в некоторых случаях свести исследование и решение дифференциальных, псевдодифференциальных, интегральных уравнений, к более простым алгебраическим задачам.

Изучая преобразование Лапласа, мы вводим оригинал функции $f(t)$ и ее изображение $F(p)$, находимое по формуле:

$$F(p) = \int_0^\infty f(t) e^<-pt>dt$$

Для быстроты и удобства решения задач составлена таблица изображений и оригиналов, которая, наряду с теоремами (линейности, подобия, смещения, запаздывания), свойствами и правилами дифференцирования и интегрирования изображения/оригинала, постоянно используется в решении примеров.

В этом разделе вы найдете готовые задания разного типа: восстановление оригинала или изображения функции, нахождение свертки функций, решение ДУ, систем ДУ или интегральных уравнений с помощью преобразования Лапласа и т.д.

Как найти изображение функции

Задача 1. Найти изображение данного оригинала, или оригинала, удовлетворяющего данному уравнению

Задача 2. Пользуясь определением, найти изображение функции $f(t)=3^t$.

Задача 3. Найти изображение функции: $\int_0^t \cos \tau \cdot e^<-3\tau>d\tau. $

Задача 4. Найти изображение оригинала $f(x)$ двумя способами:
1) Вычислив интеграл $F(p) = \int_0^\infty f(x) e^<-px>dx$;
2) Воспользовавшись таблице изображений и свойствами преобразования Лапласа.
Оригинал задается формулой (курсочно-линейная функция, см. файл).

Как найти оригинал функции

Задача 5. Найти оригинал изображения $F(p)$, где

Задача 6. Найти оригинал изображения

Задача 7. Найти оригинал для функции с помощью вычетов

Как решить ДУ (систему ДУ) операционным методом

Задача 8. Найти частное решение дифференциального уравнения с заданными начальными условиями операторным методом

Задача 9. Найти решение задачи Коши методами операционного исчисления

Задача 10. Методом операционного исчисления найти частное решение системы дифференциальных уравнений, удовлетворяющее заданным начальным условиям.

Задача 11. Методом операционного исчисления найти решение задачи Коши для ДУ 3-го порядка

Задача 12. Решите задачу Коши для системы дифференциальных уравнений с помощью преобразования Лапласа.

Задача 13. C помощью формулы Дюамеля найти решение уравнения

Задача 14. Решить систему ДУ с помощью преобразования Лапласа

Как решить интегральное уравнение

Задача 15. Методом операционного исчисления найти решение интегрального уравнения

$$ y(t)=\cos t +\int_0^t (t-\tau)^2 y(\tau)d \tau. $$

Задача 16. Решить интегральное уравнение

$$ \int_0^t ch (\tau) x(t-\tau)d \tau = t. $$

Как найти свертку функций

Задача 17. Найти свертку функций $f(t)=1$ и $\phi(t)=\sin 5t$.

Помощь с решением заданий

Если вам нужна помощь с решением задач и контрольных по этой и другим темам математического анализа, обращайтесь в МатБюро. Стоимость подробной консультации от 100 рублей , оформление производится в Word, срок от 1 дня.

Конспект лекций по дисциплине «Математический аппарат теории сигналов и систем» (стр. 5 )

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7

.

15. Уравнение типа свертки

Это такие интегральные уравнения, ядро которых зависит от разности аргументов. Они имеют следующий вид:

Для решения уравнений типа свертки используется преобразование Фурье в следующей форме:

Введем понятие свертка функций. Она представляет из себя следующее:

Интегральный оператор Фурье будем обозначатьF(*).

Преобразование Фурье от свертки функций равно произведению отдельных преобразований Фурье от каждой функции:

Тогда после преобразования Фурье:

Отсюда можно найти :

Взяв обратное преобразование Фурье, мы получаем нашу функцию:

Пусть — это обратное преобразование Фурье от следующей функции:

Тогда решение можно найти по формуле:

16. Применение метода свертки для решения

интегральных уравнений 1-го рода

Бывают уравнения типа свертки и 1-го рода, то есть неизвестная функция есть только под знаком интеграла. Здесь также применим этот метод:

Преобразование Лапласа можно также применять как и Фурье, но нужно всегда при решении проверять область определения.

L — так будем обозначать преобразование Лапласа.

Взяв преобразование Лапласа от , получим:

Решение системы интегральных уравнений

Пусть имеем систему N интегральных уравнений следующего вида:

Применим ко всем уравнениям этой системы преобразование Лапласа:

Решив эту систему алгебраических уравнений в виде набора изображений и найдя от них оригиналы, мы найдем решение:

Это нелинейное уравнение типа свертки. Применим преобразование Лапласа к обеим частям этого уравнения:

Это квадратное уравнение, его решение:

17. Решение интегро-дифференциальных уравнений типа свертки

Пусть дано следующее интегро-дифференциальное уравнение:

Набор начальных условий:

Используется следующее свойство преобразования Лапласа:

Применим это к нашему уравнению:

Теперь общее уравнение превращается в следующий вид:

Отсюда изображение искомой функции:

Преобразование Меллина

Пусть есть некая функция и для нее справедливо следующее:

Для такой функции есть преобразование Меллина:

,

Преобразование Меллина устанавливает однозначную взаимосвязь между 2-мя функциями. Интеграл берется на комплексной плоскости вверх и вниз.

Гамма-функция. С помощью преобразования Меллина гамма-функция вводится следующим образом:

Преобразование Меллина во многом похоже на преобразование Лапласа:

.

Есть следующая взаимосвязь:

18. Применение преобразования Меллина для решения

;

;

.

Это свойство используется для решения интегрального уравнения вида:

. (*)

Преобразование Меллина используется для решения уравнений типа (*). Условие применимости этих функций состоит в том, чтобы они допускали от себя преобразование Меллина. Обозначим преобразование Меллина от через , а преобразование Меллина от — . Функции и должны иметь общую область аналитичности. Применим преобразование Меллина к обеим частям уравнения (*).

;

.

Пусть имеем интегральное уравнение вида:

;

;

;

;

;

.

19. Симметричные интегральные уравнения

Симметричными называются интегральные уравнения вида:

;

.

Если ядро комплексно — значное, то

;

;

— линейный оператор под функцией .

Если бы , то соответствующее интегральное уравнение стало бы однородным. При этом можно записать следующее: . Выяснили, что такое однородное уравнение имеет ограниченное число решений. Эти решения представляют собой набор некоторых функций . Они называются собственными функциями. Они однозначно соответствуют собственным числам.

Если мы рассматриваем симметричные ядра, то справедливы следующие свойства:

Сверточный слой: методы оптимизации основанные на матричном умножении

Введение

Данная статья является продолжением серии статей описывающей алгоритмы лежащие в основе
Synet — фреймворка для запуска предварительно обученных нейронных сетей на CPU.

Если смотреть на распределение процессорного времени, которое тратится на прямое распространение сигнала в нейронных сетях, то окажется что зачастую более 90% всего времени тратится в свёрточных слоях. Поэтому если мы хотим получить быстрый алгоритм для нейронной сети – нам нужен, прежде всего, быстрый алгоритм для свёрточного слоя. В настоящей статье я хочу описать методы оптимизации прямого распространения сигнала в свёрточном слое. Причем начать хочется с наиболее широко распространенных методов, основанных на матричном умножении. Изложение я буду стараться вести в максимально доступной форме, чтобы статья была интересна не только специалистам (они и так про это все знают), но и более широкому кругу читателей. Я не претендую на полноту обзора, так что любые замечания и дополнения только приветствуются.

Параметры свёрточного слоя

Начать описание хотелось бы с описания параметров, которые есть в свёрточном слое. Специалисты могут смело пропустить этот раздел.

Размеры входного и выходного изображения

Прежде всего, свёрточный слой характеризуется входным и выходным изображением, которые характеризуются следующими параметрами:

• srcC / dstC — число каналов во входном и выходном изображении. Альтернативные обозначения: C / D.
• srcH / dstH — высота входного и выходного изображения. Альтернативное обозначение: H.
• srcW / dstW — ширина входного и выходного изображения. Альтернативное обозначение: W.
• batch — число входных (выходных) изображений — слой за раз может обработать целую партию изображений. Альтернативное обозначение: N.

Размеры ядра свертки

Операция свертки по своей сути — это взвешенная сумма некой окрестности данной точки изображения. Размер ядра свертки — характеризует величину этой окрестности и описывается двумя параметрами:

• kernelY — высота ядра свертки. Альтернативное обозначение: Y.
• kernelX — ширина ядра свертки. Альтернативное обозначение: X.

Наиболее часто встречаются свертки с размером ядра 1×1 и 3×3. Размеры 5×5 и 7×7 встречаются значительно реже. Большие размеры свертки, а также свертки с ядром отличным от квадратного тоже иногда встречаются, но это больше экзотика.

Шаг свертки

Еще один важный параметр — шаг свертки:

• strideY — вертикальный шаг свертки.
• strideX — горизонтальный шаг свертки.

Если шаг отличен от 1×1, например — 2×2, то выходное изображение будет в два раза меньше (свертка будет рассчитана только в окрестности четных точек).

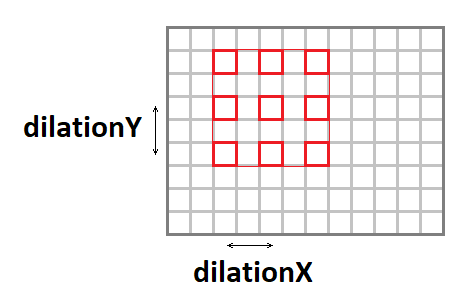
Растяжение свертки

Ядро свертки можно растянуть (увеличить эффективный размер окна, при сохранении количества операций) при помощи следующих параметров:

• dilationY — вертикальное растяжение свертки.
• dilationX — горизонтальное растяжение свертки.

Стоит отметить, что случаи с растяжением, отличным от 1×1 достаточно редкое явление (так я за свою карьеру с таким ни разу не встретился).

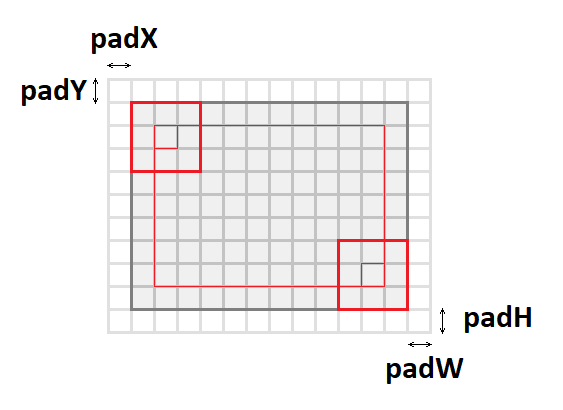
Паддинг входного изображения

Если применить свертку с окном, отличным от единичного к изображению, то выходное изображение будет меньше на величину kernel — 1. Свертка как бы «съедает» края. Чтобы сохранить размер изображения, входное изображение часто дополняют по краям нулями. За это отвечают еще четыре параметра:

• padY / padX — передние вертикальный и горизонтальный отступы.
• padH / padW — задние вертикальный и горизонтальный отступы.

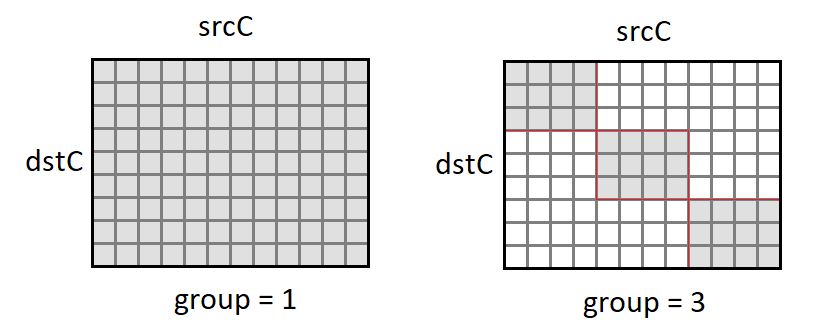
Группы каналов

Обычно каждый выходной канал представляет собой сумму сверток по всем входным каналам. Однако, это не всегда так. Есть возможность разбить входные и выходные каналы на группы, суммирование осуществляется только внутри групп:

• group — число групп.

На практике чаще всего встречаются ситуации с group = 1 и group = srcC = dstC — так называемое depthwise convolution.

Смещение и активационная функция

Хотя формально смещение и активационная функция не входят в свертку, но очень часто эти две операции следуют за свёрточным слоем, почему их обычно тоже включают в него. В виду разнообразия возможных активационных функций и их параметров, я не буду здесь их подробно описывать.

Базовая реализация алгоритма

Для начала хотелось бы привести базовую реализацию алгоритма:

В этой реализации я предполагал, что входное и выходное изображение имеет формат NCHW:

веса свертки хранятся в формате DCYX, а активационная функция у нас это ReLU. В общем случае это не так, но для базовой реализации такие предположения вполне уместны — надо же от чего-то отталкиваться.

Мы имеем 8 вложенных циклов и общее количество операций:

при этом количество данных во входном: