Олимпиадные задания. Решение уравнений в целых числах
методическая разработка по алгебре (9, 10, 11 класс) на тему
В данной работе представлены различные способы решения уравнений в целых числах. Работа может быть использована при подготовке к олимпиадам, на кружковых и факультативных занятиях.
Скачать:
| Вложение | Размер |
|---|---|
| aksanova_ii._olimpiadnye_zadaniya.reshenie_uravneniy_v_tselyh_chislah.docx | 100.62 КБ |
Предварительный просмотр:
МБОУ «Высокогорская средняя общеобразовательная школа №2
Высокогорского муниципального района Республики Татарстан»
Решение уравнений в целых числах
Аксанова Ильсияр Исмагиловна
Учитель математики высшей категории
С. Высокая Гора – 2015 г.
Работа посвящена решению уравнений в целых числах. Актуальность этой темы обусловлена тем, что задачи, основанные на решении уравнений в целых числах, часто встречаются на вступительных экзаменах в высшие учебные заведения и на олимпиадах по математике и на ЕГЭ в старших классах. В школьной программе эта тема рассматривается в ознакомительном порядке. В работе представлены различные способы решения уравнений в целых числах, разобраны конкретные примеры. Данная работа будет полезна учителям старших классов для подготовки к ЕГЭ и олимпиадам.
Уравнения в целых числах – это алгебраические уравнения с двумя или более неизвестными переменными и целыми коэффициентами. Решениями такого уравнения являются все целочисленные наборы значений неизвестных переменных, удовлетворяющих этому уравнению. Такие уравнения ещё называют диофантовыми , в честь древнегреческого математика Диофанта Аксандрийского, который исследовал некоторые типы таких уравнений ещё до нашей эры.
Наиболее известное уравнение в целых числах – великая теорема Ферма: уравнение
не имеет ненулевых рациональных решений для всех натуральных n > 2.
При решении уравнений в целых и натуральных числах можно условно выделить следующие способы решения:
- способ перебора вариантов;
- применение алгоритма Евклида;
- применение цепных дробей;
- разложения на множители;
- решение уравнений в целых числах как квадратных относительно какой-либо переменной;
- метод остатков;
- метод бесконечного спуска;
- оценка выражений, входящих в уравнение.
В работе представлены два приложения: п риложение 1. Таблица остатков при делении степеней ( a n : m ); приложение 2. Задачи для самостоятельного решения
1. Способ перебора вариантов.
Пример 1.1. Найти множество всех пар натуральных чисел, которые являются решениями уравнения 49 х + 51 у = 602.
Решение. Выразим из уравнения переменную х через у х = , так как х и у – натуральные числа, то
х = 602 — 51 у ≥ 49, 51 у ≤553, 1≤ у ≤10 .
Полный перебор вариантов показывает, что натуральными решениями уравнения являются х =5, у =7.
2. Применение алгоритма Евклида. Теорема.
Дано уравнение ax+by=c , где a, b, c -целые числа, a и b не равны 0.
Теорема: Если c не делится нацело на НОД( a,b ), то уравнение не разрешимо в целых числах. Если НОД( a,b )=1или c делится на НОД( a,b ), то уравнение разрешимо в целых числах. Если (x 0 , y 0 )- какое-нибудь решение уравнения, то все решения уравнения задаются формулами:
y=y 0 +at , где t — принадлежит множеству целых чисел.
Пример 2.1. Решить уравнение в целых числах 5 х + 7 у = 19
Подберём сначала некоторое конкретное решение. В данном случае, это просто, например,
Тогда 5 x 0 + 7 y 0 = 19, откуда
5( х – x 0 ) + 7( у – y 0 ) = 0,
5( х – x 0 ) = –7( у – y 0 ).
Поскольку числа 5 и 7 взаимно простые, то
х – x 0 = 7 k , у – y 0 = –5 k.
Значит, общее решение:
х = 1 + 7 k , у = 2 – 5 k ,
где k – произвольное целое число.
Ответ: (1+7 k ; 2–5 k ), где k – целое число.
Пример 2.2. Решить уравнение 201 х – 1999 у = 12.
Найти некоторое конкретное решение подбором в данном случае достаточно сложно. Воспользуемся алгоритмом Евклида для чисел 1999 и 201:
НОД(1999, 201) = НОД(201, 190) = НОД(190, 11) = НОД(11, 3) = НОД(3 , 2) = НОД(2, 1) = 1.
Запишем этот процесс в обратном порядке:
1 = 2 – 1 = 2 – (3 – 2) = 2·2 – 3 = 2· (11 – 3·3) – 3 = 2·11 – 7·3 = 2·11 – 7(190 – 11·17) =
= 121·11 – 7·190 = 121(201 – 190) – 7·190 = 121·201 – 128·190 =
= 121·201 – 128(1999 – 9·201) = 1273·201 – 128·1999.
Значит, пара (1273, 128) является решением уравнения 201 х – 1999 у = 1. Тогда пара чисел
x 0 = 1273·12 = 15276, y 0 = 128·12 = 1536
является решением уравнения 201 х – 1999 у = 12.
Общее решение этого уравнения запишется в виде
х = 15276 + 1999 k , у = 1536 + 201 k , где k – целое число,
или, используя, что 15276 = 1283 + 7·1999, 1536 = 129 + 7·201, имеем
х = 1283 + 1999 n , у = 129 + 201 n , где n – целое число.
Ответ: (1283+1999 n , 129+201 n ), где n – целое число.
3. Метод остатков.
Этот метод основан на исследовании возможных остатков левой и правой частей уравнения от деления на некоторое фиксированное натуральное число.
Замечание . Говоря строго математическим языком, для решения уравнения в данном случае применяется теория сравнений.
Рассмотрим примеры, которые раскрывают сущность данного метода.
Пример 3.1. Решить уравнение в целых числах x 3 + y 3 = 3333333;
Так как x 3 и y 3 при делении на 9 могут давать только остатки 0, 1 и 8 (смотрите таблицу в приложении 1), то x 3 + y 3 может давать только остатки 0, 1, 2, 7 и 8. Но число 3333333 при делении на 9 даёт остаток 3. Поэтому исходное уравнение не имеет решений в целых числах.
Ответ: целочисленных решений нет.
Пример 3.2. Решить уравнение в целых числах x 3 + y 3 = 4( x 2 y + xy 2 + 1).
Перепишем исходное уравнение в виде ( x + y ) 3 = 7( x 2 y + xy 2 ) + 4. Так как кубы целых чисел при делении на 7 дают остатки 0, 1 и 6, но не 4, то уравнение не имеет решений в целых числах.
Ответ: целочисленных решений нет.
Пример 3.3. Решить в целых числах уравнение x 2 + 1 = 3 y .
Решение. Заметим, что правая часть уравнения делится на 3 при любом целом y .
Исследуем какие остатки может иметь при делении на три левая часть этого уравнения.По теореме о делении с остатком целое число х либо делится на 3, либо при делении на три в остатке дает 1 или 2.
Если х = 3 k , то правая часть уравнения на 3 не делится.
Если х = 3 k+ 1, то x 2 + 1= (3 k+ 1) 2 +1=3 m +2, следовательно, опять левая часть на 3 не делится.
Если х = 3 k+ 2, то x 2 + 1= (3 k+ 2) 2 +1=3 m +2, следовательно, и в этом случае левая часть уравнения на три не делится.
Таким образом, мы получили, что ни при каких целых х левая часть уравнения на 3 не делится, при том, что левая часть уравнения делится на три при любых значениях переменной y . Следовательно, уравнение в целых числах решений не имеет.
Ответ: целочисленных решений нет.
Пример 3.4. Решить в целых числах x³ — 3y³ — 9z³ = 0 (1)
Решение. Очевидно, что решением уравнения будет тройка чисел (0; 0; 0).
Выясним, имеет ли уравнение другие решения. Для этого преобразуем уравнение (1) к виду
x ³ = 3 y ³ + 9 z ³ (2)
Так как правая часть полученного уравнения делится на 3, то и левая должна делиться на три, следовательно, так как 3 — число простое, х делится на 3, т.е. х = 3 k , подставим это выражение в уравнение (2), получим:
27 k 3 = 3 y ³ + 9 z ³, откуда
9 k 3 = y ³ + 3 z ³ (3)
следовательно, y ³ делится на 3 и y = 3 m . Подставим полученное выражение в уравнение (3): 9 k 3 = 27 m ³ + 3 z ³, откуда
3 k 3 = 9 m ³ + z ³ (4)
В свою очередь, из этого уравнения следует, что z 3 делится на 3, и z = 3 n . Подставив это выражение в (4), получим, что k 3 должно делиться на 3.
Итак, оказалось, что числа, удовлетворяющие первоначальному уравнению, кратны трём, и сколько раз мы не делили бы их на 3, опять должны получаться числа, кратные трём. Единственное целое число, удовлетворяющее этому условию, будет нуль, т. е. решение данного уравнения (0; 0; 0) является единственным.
4. Решение уравнений в целых числах сведением их к квадратным.
Пример 4.1. Решить в простых числах уравнение
х 2 – 7 х – 144 = у 2 – 25 у .
Решим данное уравнение как квадратное относительно переменной у . Получим: у = х + 9 или у = 16 – х .
Поскольку при нечётном х число х + 9 является чётным, то единственной парой простых чисел, которая удовлетворяет первому равенству, является (2; 11).
Так как х, у – простые, то из равенства у = 16 – х , имеем
С помощью перебора вариантов находим остальные решения: (3; 13), (5; 11), (11; 5), (13; 3).
Ответ: (2; 11), (3; 13), (5; 11), (11; 5), (13; 3).
Пример 4.2 . Решить в целых числах уравнение x + y = x 2 – xy + y 2 .
Рассмотрим данное уравнение как квадратное уравнение относительно x :
x 2 – ( y + 1) x + y 2 – y = 0.
Дискриминант этого уравнения равен –3 y 2 + 6 y + 1. Он положителен лишь для следующих значений у : 0, 1, 2. Для каждого из этих значений из исходного уравнения получаем квадратное уравнение относительно х , которое легко решается.
Ответ: (0; 0), (0; 1), (1; 0), (1; 2), (2; 1), (2; 2).
Пример 4.3 . Решить уравнение в целых числах: 5 х 2 +5 у 2 +8 ху +2 у -2 х +2=0.
Рассмотрим уравнение как квадратное относительно х:
5 х 2 + (8 у — 2) х + 5 у 2 + 2 у + 2 = 0
D = (8 у — 2) 2 — 4·5(5 у 2 + 2 у + 2) = 64 у 2 — 32 у + 4 = -100 у 2 — 40 у – 40 = = -36( у 2 + 2 у + 1) = -36( у + 1) 2
Для того, чтобы уравнение имело решения, необходимо, чтобы D = 0.
-36( у + 1) 2 = 0. Это возможно при у = -1, тогда х = 1.
5. Разложение на множители .
Пример 5.1. Решить в целых числах уравнение x 2 – xy – 2 y 2 = 7.
Разложим левую часть на множители ( x – 2 y )( x + y ) = 7.
Так как х, у – целые числа, то находим решения исходного уравнения, как решения следующих четырёх систем:
1) x – 2 y = 7, x + y = 1;
2) x – 2 y = 1, x + y = 7;
3) x – 2 y = –7, x + y = –1;
4) x – 2 y = –1, x + y = –7.
Решив эти системы, получаем решения уравнения: (3; –2), (5; 2), (–3; 2) и (–5; –2).
Ответ: (3; –2), (5; 2), (–3; 2), (–5; –2).
Пример 5.2 . Решить уравнение в целых числах: х 2 + 23 = у 2
Решение. Перепишем уравнение в виде:
у 2 — х 2 = 23, ( у — х )( у + х ) = 23
Так как х и у – целые числа и 23 – простое число, то возможны случаи:
Решая полученные системы, находим:
Пример 5.3 . Решить уравнение в целых числах y 3 — x 3 = 91.
Решение. Используя формулы сокращенного умножения, разложим правую часть уравнения на множители:
( y — x )( y 2 + xy + x 2 ) = 91
Выпишем все делители числа 91: ± 1; ± 7; ± 13; ± 91
Проводим исследование. Заметим, что для любых целых x и y число
y 2 + yx + x 2 ≥ y 2 — 2| y || x | + x 2 = (| y | — | x |) 2 ≥ 0,
следовательно, оба сомножителя в левой части уравнения должны быть положительными. Тогда уравнение равносильно совокупности систем уравнений:
Решив системы, получим: первая система имеет решения (5; 6), (-6; -5); третья (-3; 4),(-4;3); вторая и четвертая решений в целых числах не имеют.
Пример 5.4 . Решить в целых числах уравнение x + y = xy .
Решение. Перенесем все члены уравнения влево и к обеим частям полученного уравнения прибавим (–1)
x + y – xy – 1 = – 1
Сгруппируем первое – четвертое и второе – третье слагаемые и вынесем общие множители, в результате получим уравнение: ( x — 1)( y — 1) = 1
Произведение двух целых чисел может равняться 1 в том и только в том случае, когда оба этих числа равны или 1, или (–1). Записав соответствующие системы уравнений и, решив их, получим решение исходного уравнения.
Пример 5.5 . Доказать, что уравнение ( x — y ) 3 + ( y — z ) 3 + ( z — x ) 3 = 30 не имеет решений в целых числах.
Решение. Разложим левую часть уравнения на множители и обе части уравнения разделим на 3, в результате получим уравнение:
( x — y )( y — z )( z — x ) = 10
Делителями 10 являются числа ±1, ±2, ±5, ±10. Заметим также, что сумма сомножителей левой части уравнения равна 0. Нетрудно проверить, что сумма любых трех чисел из множества делителей числа 10, дающих в произведении 10, не будет равняться 0. Следовательно, исходное уравнение не имеет решений в целых числах.
Ответ: целочисленных решений нет.
6. Метод бесконечного спуска.
Метод спуска предполагает сначала последовательное выражение одной переменой чрез другую, пока в представлении переменной не останется дробей, а затем, последовательное «восхождение» по цепочке равенств для получения общего решения уравнения.
Пример 6.1 . Решить уравнение в целых числах 5 x + 8 y = 39.
Выберем неизвестное, имеющее наименьший коэффициент , и выразим его через другое неизвестное: . Выделим целую часть: Очевидно, что х будет целым, если выражение окажется целым, что, в свою очередь, будет иметь место тогда, когда число 4 – 3 y без остатка делится на 5.
Введем дополнительную целочисленную переменную z следующим образом: 4 –3 y = 5 z . В результате получим уравнение такого же типа, как и первоначальное, но уже с меньшими коэффициентами. Решать его будем уже относительно переменной y , рассуждая аналогично: . Выделяя целую часть, получим:
Рассуждая аналогично предыдущему, вводим новую переменную
Выразим неизвестную с наименьшим коэффициентом, в этом случае переменную z : = . Требуя, чтобы было целым, получим: 1 – u = 2 v , откуда u = 1 – 2 v . Дробей больше нет, спуск закончен.
Теперь необходимо «подняться вверх». Выразим через переменную v сначала z , потом y и затем x :
z = = = 3 v – 1; = 3 – 5 v .
Формулы x = 3+8 v и y = 3 – 5 v , где v – произвольное целое число, представляют общее решение исходного уравнения в целых числах.
Ответ: x = 3+8 v и y = 3 – 5 v.
7. Оценка выражений, входящих в уравнение.
Пример 7.1. Решить в целых числах уравнение ( х 2 + 4)( у 2 + 1) = 8ху
Решение. Заметим, что если ( х ;у ) – решение уравнения, то (- х ;- у ) – тоже решение.
И так как х = 0 и у = 0 не являются решением уравнения, то, разделив обе части уравнения на ху, получим:
Пусть х > 0, у > 0, тогда, согласно неравенству Коши,
тогда их произведение ( х + )( у + ) = 4·2 = 8, значит, х + = 4 и у + = 2.
Отсюда находим х = 2 и у = 1 – решение, тогда х = -2 и у = -1 – тоже решение.
Пример 7.2 . Решить уравнение в целых числах
x 2 + 13 y 2 – 6 xy = 100
Решение . x 2 + 13 y 2 –6 xy= 100 ↔ ( x- 3 y ) 2 + 4 y 2 = 100 . Так как ( x- 3 y ) 2 ≥ 0 , то 4 y 2 ≤ 100 , или │ 2 y│≤ 10 . Аналогично, в силу 4 y 2 ≥ 0 должно выполняться │x- 3 y│≤ 10 .
math4school.ru
Уравнения в целых числах
Немного теории
Уравнения в целых числах – это алгебраические уравнения с двумя или более неизвестными переменными и целыми коэффициентами. Решениями такого уравнения являются все целочисленные (иногда натуральные или рациональные) наборы значений неизвестных переменных, удовлетворяющих этому уравнению. Такие уравнения ещё называют диофантовыми, в честь древнегреческого математика Диофанта Александрийского, который исследовал некоторые типы таких уравнений ещё до нашей эры.
Современной постановкой диофантовых задач мы обязаны французскому математику Ферма. Именно он поставил перед европейскими математиками вопрос о решении неопределённых уравнений только в целых числах. Наиболее известное уравнение в целых числах – великая теорема Ферма: уравнение
не имеет ненулевых рациональных решений для всех натуральных n > 2.
Теоретический интерес к уравнениям в целых числах достаточно велик, так как эти уравнения тесно связаны со многими проблемами теории чисел.
В 1970 году ленинградский математик Юрий Владимирович Матиясевич доказал, что общего способа, позволяющего за конечное число шагов решать в целых числах произвольные диофантовы уравнения, не существует и быть не может. Поэтому следует для разных типов уравнений выбирать собственные методы решения.
При решении уравнений в целых и натуральных числах можно условно выделить следующие методы:
способ перебора вариантов;
применение алгоритма Евклида;
представление чисел в виде непрерывных (цепных) дробей;
разложения на множители;
решение уравнений в целых числах как квадратных (или иных) относительно какой-либо переменной;
метод бесконечного спуска.
Задачи с решениями
1. Решить в целых числах уравнение x 2 – xy – 2y 2 = 7.
Запишем уравнение в виде (x – 2y)(x + y) = 7.
Так как х, у – целые числа, то находим решения исходного уравнения, как решения следующих четырёх систем:
1) x – 2y = 7, x + y = 1;
2) x – 2y = 1, x + y = 7;
3) x – 2y = –7, x + y = –1;
4) x – 2y = –1, x + y = –7.
Решив эти системы, получаем решения уравнения: (3; –2), (5; 2), (–3; 2) и (–5; –2).
Ответ: (3; –2), (5; 2), (–3; 2), (–5; –2).
2. Решить в целых числах уравнение:
а) 20х + 12у = 2013;
в) 201х – 1999у = 12.
а) Поскольку при любых целых значениях х и у левая часть уравнения делится на два, а правая является нечётным числом, то уравнение не имеет решений в целых числах.
Ответ: решений нет.
б) Подберём сначала некоторое конкретное решение. В данном случае, это просто, например,
Поскольку числа 5 и 7 взаимно простые, то
Значит, общее решение:
х = 1 + 7k, у = 2 – 5k,
где k – произвольное целое число.
Ответ: (1+7k; 2–5k), где k – целое число.
в) Найти некоторое конкретное решение подбором в данном случае достаточно сложно. Воспользуемся алгоритмом Евклида для чисел 1999 и 201:
НОД(1999, 201) = НОД(201, 190) = НОД(190, 11) = НОД(11, 3) = НОД(3 , 2) = НОД(2, 1) = 1.
Запишем этот процесс в обратном порядке:
1 = 2 – 1 = 2 – (3 – 2) = 2·2 – 3 = 2· (11 – 3·3) – 3 = 2·11 – 7·3 = 2·11 – 7(190 – 11·17) =
= 121·11 – 7·190 = 121(201 – 190) – 7·190 = 121·201 – 128·190 =
= 121·201 – 128(1999 – 9·201) = 1273·201 – 128·1999.
Значит, пара (1273, 128) является решением уравнения 201х – 1999у = 1. Тогда пара чисел
x0 = 1273·12 = 15276, y0 = 128·12 = 1536
является решением уравнения 201х – 1999у = 12.
Общее решение этого уравнения запишется в виде
х = 15276 + 1999k, у = 1536 + 201k, где k – целое число,
или, после переобозначения (используем, что 15276 = 1283 + 7·1999, 1536 = 129 + 7·201),
х = 1283 + 1999n, у = 129 + 201n, где n – целое число.
Ответ: (1283+1999n, 129+201n), где n – целое число.
3. Решить в целых числах уравнение:
а) x 3 + y 3 = 3333333;
б) x 3 + y 3 = 4(x 2 y + xy 2 + 1).
а) Так как x 3 и y 3 при делении на 9 могут давать только остатки 0, 1 и 8 (смотрите таблицу в разделе «Делимость целых чисел и остатки»), то x 3 + y 3 может давать только остатки 0, 1, 2, 7 и 8. Но число 3333333 при делении на 9 даёт остаток 3. Поэтому исходное уравнение не имеет решений в целых числах.
Ответ: целочисленных решений нет.
б) Перепишем исходное уравнение в виде (x + y) 3 = 7(x 2 y + xy 2 ) + 4. Так как кубы целых чисел при делении на 7 дают остатки 0, 1 и 6, но не 4, то уравнение не имеет решений в целых числах.
Ответ: целочисленных решений нет.
а) в простых числах уравнение х 2 – 7х – 144 = у 2 – 25у;
б) в целых числах уравнение x + y = x 2 – xy + y 2 .
а) Решим данное уравнение как квадратное относительно переменной у. Получим
у = х + 9 или у = 16 – х.
Поскольку при нечётном х число х + 9 является чётным, то единственной парой простых чисел, которая удовлетворяет первому равенству, является (2; 11).
Так как х, у – простые, то из равенства у = 16 – х имеем
С помощью перебора вариантов находим остальные решения: (3; 13), (5; 11), (11; 5), (13; 3).
Ответ: (2; 11), (3; 13), (5; 11), (11; 5), (13; 3).
б) Рассмотрим данное уравнение как квадратное уравнение относительно x:
x 2 – (y + 1)x + y 2 – y = 0.
Дискриминант этого уравнения равен –3y 2 + 6y + 1. Он положителен лишь для следующих значений у: 0, 1, 2. Для каждого из этих значений из исходного уравнения получаем квадратное уравнение относительно х, которое легко решается.
Ответ: (0; 0), (0; 1), (1; 0), (1; 2), (2; 1), (2; 2).
5. Существует ли бесконечное число троек целых чисел x, y, z таких, что x 2 + y 2 + z 2 = x 3 + y 3 + z 3 ?
Попробуем подбирать такие тройки, где у = –z. Тогда y 3 и z 3 будут всегда взаимно уничтожаться, и наше уравнение будет иметь вид
Чтобы пара целых чисел (x; y) удовлетворяла этому условию, достаточно, чтобы число x–1 было удвоенным квадратом целого числа. Таких чисел бесконечно много, а именно, это все числа вида 2n 2 +1. Подставляя в x 2 (x–1) = 2y 2 такое число, после несложных преобразований получаем:
y = xn = n(2n 2 +1) = 2n 3 +n.
Все тройки, полученные таким образом, имеют вид (2n 2 +1; 2n 3 +n; –2n 3 – n).
6. Найдите такие целые числа x, y, z, u, что x 2 + y 2 + z 2 + u 2 = 2xyzu.
Число x 2 + y 2 + z 2 + u 2 чётно, поэтому среди чисел x, y, z, u чётное число нечётных чисел.
Если все четыре числа x, y, z, u нечётны, то x 2 + y 2 + z 2 + u 2 делится на 4, но при этом 2xyzu не делится на 4 – несоответствие.
Если ровно два из чисел x, y, z, u нечётны, то x 2 + y 2 + z 2 + u 2 не делится на 4, а 2xyzu делится на 4 – опять несоответствие.
Поэтому все числа x, y, z, u чётны. Тогда можно записать, что
и исходное уравнение примет вид
Теперь заметим, что (2k + 1) 2 = 4k(k + 1) + 1 при делении на 8 даёт остаток 1. Поэтому если все числа x1, y1, z1, u1 нечётны, то x1 2 + y1 2 + z1 2 + u1 2 не делится на 8. А если ровно два из этих чисел нечётно, то x1 2 + y1 2 + z1 2 + u1 2 не делится даже на 4. Значит,
и мы получаем уравнение
Снова повторив те же самые рассуждения, получим, что x, y, z, u делятся на 2 n при всех натуральных n, что возможно лишь при x = y = z = u = 0.
7. Докажите, что уравнение
(х – у) 3 + (y – z) 3 + (z – x) 3 = 30
не имеет решений в целых числах.
Воспользуемся следующим тождеством:
(х – у) 3 + (y – z) 3 + (z – x) 3 = 3(х – у)(y – z)(z – x).
Тогда исходное уравнение можно записать в виде
(х – у)(y – z)(z – x) = 10.
Обозначим a = x – y, b = y – z, c = z – x и запишем полученное равенство в виде
Кроме того очевидно, a + b + c = 0. Легко убедиться, что с точностью до перестановки из равенства abc = 10 следует, что числа |a|, |b|, |c| равны либо 1, 2, 5, либо 1, 1, 10. Но во всех этих случаях при любом выборе знаков a, b, c сумма a + b + c отлична от нуля. Таким образом, исходное уравнение не имеет решений в целых числах.
8. Решить в целых числах уравнение 1! + 2! + . . . + х! = у 2 .
если х = 1, то у 2 = 1,
если х = 3, то у 2 = 9.
Этим случаям соответствуют следующие пары чисел:
Заметим, что при х = 2 имеем 1! + 2! = 3, при х = 4 имеем 1! + 2! + 3! + 4! = 33 и ни 3, ни 33 не являются квадратами целых чисел. Если же х > 5, то, так как
5! + 6! + . . . + х! = 10n,
можем записать, что
1! + 2! + 3! + 4! + 5! + . . . + х! = 33 + 10n.
Так как 33 + 10n – число, оканчивающееся цифрой 3, то оно не является квадратом целого числа.
Ответ: (1; 1), (1; –1), (3; 3), (3; –3).
9. Решите следующую систему уравнений в натуральных числах:
a 3 – b 3 – c 3 = 3abc, a 2 = 2(b + c).
3abc > 0, то a 3 > b 3 + c 3 ;
таким образом имеем
b 2 2 + х = у 4 + у 3 + у 2 + у.
Разложив на множители обе части данного уравнения, получим:
х(х + 1) = у(у + 1)(у 2 + 1),
х(х + 1) = (у 2 + у)(у 2 + 1)
Такое равенство возможно, если левая и правая части равны нулю, или представляют собой произведение двух последовательных целых чисел. Поэтому, приравнивая к нулю те или иные множители, получим 4 пары искомых значений переменных:
Произведение (у 2 + у)(у 2 + 1) можно рассматривать как произведение двух последовательных целых чисел, отличных от нуля, только при у = 2. Поэтому х(х + 1) = 30, откуда х5 = 5, х6 = –6. Значит, существуют ещё две пары целых чисел, удовлетворяющих исходному уравнению:
Ответ: (0; 0), (0; –1), (–1; 0), (–1; –1), (5; 2), (–6; 2.)
Задачи без решений
1. Решить в целых числах уравнение:
б) х 2 + у 2 = х + у + 2.
2. Решить в целых числах уравнение:
а) х 3 + 21у 2 + 5 = 0;
б) 15х 2 – 7у 2 = 9.
3. Решить в натуральных числах уравнение:
4. Доказать, что уравнение х 3 + 3у 3 + 9z 3 = 9xyz в рациональных числах имеет единственное решение
5. Доказать, что уравнение х 2 + 5 = у 3 в целых числах не имеет решений.
ЛОГИКА И ДОКАЗАТЕЛЬСТВО Введение в раздел Логика необходима
ЛОГИКА И ДОКАЗАТЕЛЬСТВО» src=»https://present5.com/presentacii/20170505/23-razdel_2_logika_i_dokazatelystvo.ppt_images/23-razdel_2_logika_i_dokazatelystvo.ppt_0.jpg» alt=»>ЛОГИКА И ДОКАЗАТЕЛЬСТВО» /> ЛОГИКА И ДОКАЗАТЕЛЬСТВО
Введение в раздел Логика необходима в любой формальной дисциплине и состоит из правил получения» src=»https://present5.com/presentacii/20170505/23-razdel_2_logika_i_dokazatelystvo.ppt_images/23-razdel_2_logika_i_dokazatelystvo.ppt_1.jpg» alt=»>Введение в раздел Логика необходима в любой формальной дисциплине и состоит из правил получения» /> Введение в раздел Логика необходима в любой формальной дисциплине и состоит из правил получения обоснованного вывода (заключения). Логику можно выделить из контекста тех дисциплин, в которых она используется, и изучать как отдельный раздел науки. Акцент в этой части курса будет сделан именно на логике, лежащей в основе неоспоримых рассуждений и доказательств.
Мы познакомимся с логикой высказываний, имеющей дело с истинностью (или ложностью) простых описательных утверждений,» src=»https://present5.com/presentacii/20170505/23-razdel_2_logika_i_dokazatelystvo.ppt_images/23-razdel_2_logika_i_dokazatelystvo.ppt_2.jpg» alt=»>Мы познакомимся с логикой высказываний, имеющей дело с истинностью (или ложностью) простых описательных утверждений,» /> Мы познакомимся с логикой высказываний, имеющей дело с истинностью (или ложностью) простых описательных утверждений, что можно рассматривать как короткое введение в логику предикатов. Скажем сразу, что предикатами принято называть утверждения, содержащие переменные величины.
Кроме того, мы рассмотрим различные методы доказательств (прямое рассуждение, метод «от противного» и обратное» src=»https://present5.com/presentacii/20170505/23-razdel_2_logika_i_dokazatelystvo.ppt_images/23-razdel_2_logika_i_dokazatelystvo.ppt_3.jpg» alt=»>Кроме того, мы рассмотрим различные методы доказательств (прямое рассуждение, метод «от противного» и обратное» /> Кроме того, мы рассмотрим различные методы доказательств (прямое рассуждение, метод «от противного» и обратное рассуждение), снабженные простыми примерами проверки фактов о четных и нечетных числах, иллюстрирующими методологию рассуждений. Наконец, мы рассмотрим сильный метод доказательства, называемый методом математической индукции.
Высказывания и логика Стандартными блоками формальной логики являются высказывания. Высказыванием называется утверждение,» src=»https://present5.com/presentacii/20170505/23-razdel_2_logika_i_dokazatelystvo.ppt_images/23-razdel_2_logika_i_dokazatelystvo.ppt_4.jpg» alt=»>Высказывания и логика Стандартными блоками формальной логики являются высказывания. Высказыванием называется утверждение,» /> Высказывания и логика Стандартными блоками формальной логики являются высказывания. Высказыванием называется утверждение, которое имеет значение истинности, то есть может быть истинным (обозначается буквой И) или ложным (обозначается буквой Л). Например, земля плоская; Анна — доктор; 17 — простое число.
Каждое из высказываний можно обозначить своей буквой. Пусть, например, Р обозначает высказывание «земля плоская»,» src=»https://present5.com/presentacii/20170505/23-razdel_2_logika_i_dokazatelystvo.ppt_images/23-razdel_2_logika_i_dokazatelystvo.ppt_5.jpg» alt=»>Каждое из высказываний можно обозначить своей буквой. Пусть, например, Р обозначает высказывание «земля плоская»,» /> Каждое из высказываний можно обозначить своей буквой. Пусть, например, Р обозначает высказывание «земля плоская», Q — «Анна — доктор» и R — «17 — простое число». Используя такие логические операции, как не, или, и, можно построить новые, так называемые составные высказывания, компонуя более простые.
Например, (не Р) — это высказывание «земля не плоская»; (Р или Q) -» src=»https://present5.com/presentacii/20170505/23-razdel_2_logika_i_dokazatelystvo.ppt_images/23-razdel_2_logika_i_dokazatelystvo.ppt_6.jpg» alt=»>Например, (не Р) — это высказывание «земля не плоская»; (Р или Q) -» /> Например, (не Р) — это высказывание «земля не плоская»; (Р или Q) — «земля плоская или Анна — доктор»; (Р и Q) — «земля плоская и Анна — доктор».
Пример 2.1. Обозначим через Р высказывание «логика — забава», а через Q — «сегодня» src=»https://present5.com/presentacii/20170505/23-razdel_2_logika_i_dokazatelystvo.ppt_images/23-razdel_2_logika_i_dokazatelystvo.ppt_7.jpg» alt=»>Пример 2.1. Обозначим через Р высказывание «логика — забава», а через Q — «сегодня» /> Пример 2.1. Обозначим через Р высказывание «логика — забава», а через Q — «сегодня пятница». Требуется выразить каждое из следующих составных высказываний в символьной форме. (а) Логика — не забава, и сегодня пятница. (б) Сегодня не пятница, да и логика — не забава. (в) Либо логика — забава, либо сегодня пятница.
Решение: (а) (не Р) и Q. (б) (не Р) и (не Q). (в) Р» src=»https://present5.com/presentacii/20170505/23-razdel_2_logika_i_dokazatelystvo.ppt_images/23-razdel_2_logika_i_dokazatelystvo.ppt_8.jpg» alt=»>Решение: (а) (не Р) и Q. (б) (не Р) и (не Q). (в) Р» /> Решение: (а) (не Р) и Q. (б) (не Р) и (не Q). (в) Р или Q.
Чтобы уметь определять значение истинности составных высказываний, нам необходимо разобраться со смыслом логических операций,» src=»https://present5.com/presentacii/20170505/23-razdel_2_logika_i_dokazatelystvo.ppt_images/23-razdel_2_logika_i_dokazatelystvo.ppt_9.jpg» alt=»>Чтобы уметь определять значение истинности составных высказываний, нам необходимо разобраться со смыслом логических операций,» /> Чтобы уметь определять значение истинности составных высказываний, нам необходимо разобраться со смыслом логических операций, т. е. какой эффект они оказывают на истинностное значение простых высказываний. Это можно аккуратно сделать с помощью так называемых таблиц истинности.
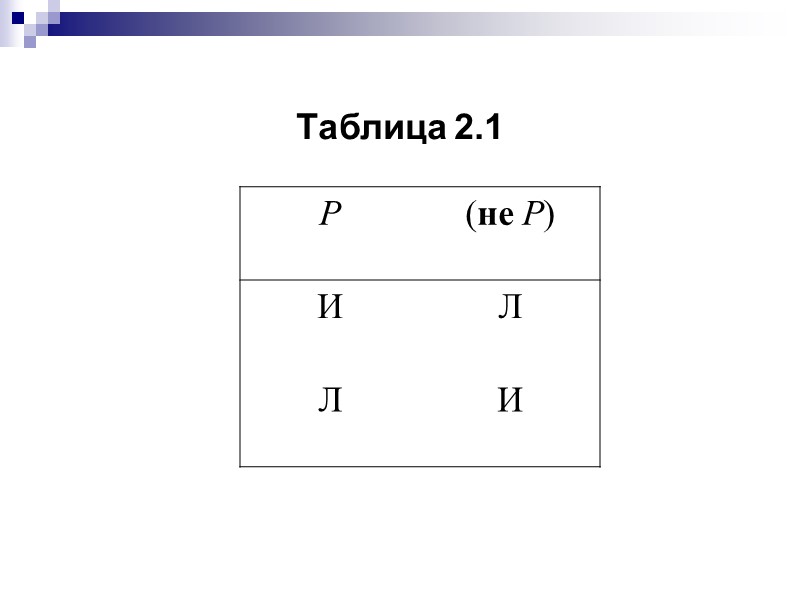
Отрицанием произвольного высказывания Р называется высказывание вида (не Р), чье истинностное значение строго противоположно» src=»https://present5.com/presentacii/20170505/23-razdel_2_logika_i_dokazatelystvo.ppt_images/23-razdel_2_logika_i_dokazatelystvo.ppt_10.jpg» alt=»>Отрицанием произвольного высказывания Р называется высказывание вида (не Р), чье истинностное значение строго противоположно» /> Отрицанием произвольного высказывания Р называется высказывание вида (не Р), чье истинностное значение строго противоположно значению Р. Определяющая таблица истинности отрицания высказывания приведена в табл. 2.1.
Таблица 2.1″ src=»https://present5.com/presentacii/20170505/23-razdel_2_logika_i_dokazatelystvo.ppt_images/23-razdel_2_logika_i_dokazatelystvo.ppt_11.jpg» alt=»>Таблица 2.1″ /> Таблица 2.1
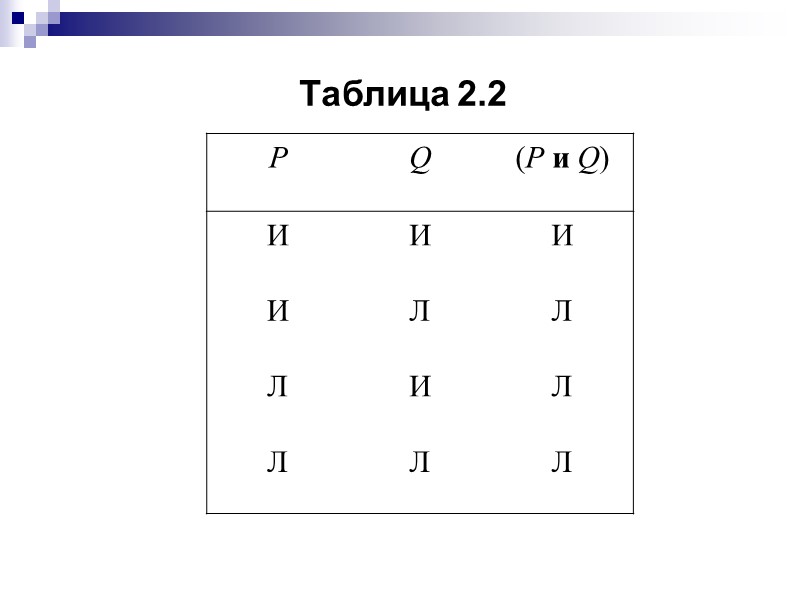
Конъюнкцией или логическим умножением двух высказываний Р и Q называют составное высказывание вида (Р» src=»https://present5.com/presentacii/20170505/23-razdel_2_logika_i_dokazatelystvo.ppt_images/23-razdel_2_logika_i_dokazatelystvo.ppt_12.jpg» alt=»>Конъюнкцией или логическим умножением двух высказываний Р и Q называют составное высказывание вида (Р» /> Конъюнкцией или логическим умножением двух высказываний Р и Q называют составное высказывание вида (Р и Q). Оно принимает истинное значение только в том случае, когда истинны обе его составные части. Такое определение хорошо согласуется с обычным пониманием союза «и» в разговорном языке. Соответствующая таблица истинности — это табл. 2.2.
Таблица 2.2″ src=»https://present5.com/presentacii/20170505/23-razdel_2_logika_i_dokazatelystvo.ppt_images/23-razdel_2_logika_i_dokazatelystvo.ppt_13.jpg» alt=»>Таблица 2.2″ /> Таблица 2.2
Дизъюнкцией или логическим сложением двух высказываний Р и Q называется составное высказывание (Р или» src=»https://present5.com/presentacii/20170505/23-razdel_2_logika_i_dokazatelystvo.ppt_images/23-razdel_2_logika_i_dokazatelystvo.ppt_14.jpg» alt=»>Дизъюнкцией или логическим сложением двух высказываний Р и Q называется составное высказывание (Р или» /> Дизъюнкцией или логическим сложением двух высказываний Р и Q называется составное высказывание (Р или Q). Оно истинно, если хотя бы одна из ее составных частей имеет истинное значение, что в некотором смысле также согласуется с обыденным пониманием союза «или». Другими словами, (Р или Q) означает, что «или Р, или Q, или и то, и другое». Таблица истинности дизъюнкции обозначена как табл. 2.3.
Таблица 2.3″ src=»https://present5.com/presentacii/20170505/23-razdel_2_logika_i_dokazatelystvo.ppt_images/23-razdel_2_logika_i_dokazatelystvo.ppt_15.jpg» alt=»>Таблица 2.3″ /> Таблица 2.3
Пример 2.2. Что можно сказать об истинности составного высказывания: «либо Луна состоит из сыра» src=»https://present5.com/presentacii/20170505/23-razdel_2_logika_i_dokazatelystvo.ppt_images/23-razdel_2_logika_i_dokazatelystvo.ppt_16.jpg» alt=»>Пример 2.2. Что можно сказать об истинности составного высказывания: «либо Луна состоит из сыра» /> Пример 2.2. Что можно сказать об истинности составного высказывания: «либо Луна состоит из сыра и у английского короля Генриха VIII было шесть жен, либо не верно, что птица дронт вымерла»?
Решение. Обозначим через Р высказывание «Луна состоит из сыра», через Q — «у Генриха» src=»https://present5.com/presentacii/20170505/23-razdel_2_logika_i_dokazatelystvo.ppt_images/23-razdel_2_logika_i_dokazatelystvo.ppt_17.jpg» alt=»>Решение. Обозначим через Р высказывание «Луна состоит из сыра», через Q — «у Генриха» /> Решение. Обозначим через Р высказывание «Луна состоит из сыра», через Q — «у Генриха VIII было шесть жен» и через R — «птица дронт вымерла». Символьная запись данного высказывания имеет вид: (Р и Q) или (не R). Известно, что высказывание Р ложно, a Q и R истинны. Поэтому высказывание (Р и Q) или (не R) имеет такое истинностное значение: (Л и И) или (Л) = Л или Л, что эквивалентно Л.
Два составных высказывания, построенные из одних и тех же простых утверждений, но разными путями,» src=»https://present5.com/presentacii/20170505/23-razdel_2_logika_i_dokazatelystvo.ppt_images/23-razdel_2_logika_i_dokazatelystvo.ppt_18.jpg» alt=»>Два составных высказывания, построенные из одних и тех же простых утверждений, но разными путями,» /> Два составных высказывания, построенные из одних и тех же простых утверждений, но разными путями, могут принимать одинаковые значения истинности на любом возможном наборе значений истинности своих составных частей. Такие высказывания называются логически эквивалентными.
Пример 2.3. Показать, что высказывание (не (Р и (не Q))) логически эквивалентно утверждению» src=»https://present5.com/presentacii/20170505/23-razdel_2_logika_i_dokazatelystvo.ppt_images/23-razdel_2_logika_i_dokazatelystvo.ppt_19.jpg» alt=»>Пример 2.3. Показать, что высказывание (не (Р и (не Q))) логически эквивалентно утверждению» /> Пример 2.3. Показать, что высказывание (не (Р и (не Q))) логически эквивалентно утверждению ((не Р) или Q). Решение. Заполним совместную таблицу истинности (табл. 2.4) для составных высказываний: R = (не (Р и (не Q))) и S= ((не Р) или Q). Вспомогательные колонки таблицы используются для построения обоих выражений из Р и Q.
Две последние колонки этой таблицы идентичны. Это означает, что высказывание R логически эквивалентно высказыванию» src=»https://present5.com/presentacii/20170505/23-razdel_2_logika_i_dokazatelystvo.ppt_images/23-razdel_2_logika_i_dokazatelystvo.ppt_20.jpg» alt=»>Две последние колонки этой таблицы идентичны. Это означает, что высказывание R логически эквивалентно высказыванию» /> Две последние колонки этой таблицы идентичны. Это означает, что высказывание R логически эквивалентно высказыванию S. Таблица 2.4
Важно изучить еще один тип логического оператора, результатом которого является условное высказывание. Примером такого» src=»https://present5.com/presentacii/20170505/23-razdel_2_logika_i_dokazatelystvo.ppt_images/23-razdel_2_logika_i_dokazatelystvo.ppt_21.jpg» alt=»>Важно изучить еще один тип логического оператора, результатом которого является условное высказывание. Примером такого» /> Важно изучить еще один тип логического оператора, результатом которого является условное высказывание. Примером такого высказывания является следующее: «если завтра будет суббота, то сегодня — пятница». При определении истинностного значения условного высказывания, необходимо различать фактическую истину и логическую.
В логике условное высказывание «если Р, то Q» принято считать ложным только в том» src=»https://present5.com/presentacii/20170505/23-razdel_2_logika_i_dokazatelystvo.ppt_images/23-razdel_2_logika_i_dokazatelystvo.ppt_22.jpg» alt=»>В логике условное высказывание «если Р, то Q» принято считать ложным только в том» /> В логике условное высказывание «если Р, то Q» принято считать ложным только в том случае, когда предпосылка Р истинна, а заключение Q ложно. В любом другом случае оно считается истинным. Используя символ импликации « », мы пишем Р Q для обозначения условного высказывания «если Р, то Q». Такая запись читается как «из Р следует Q» или, «Р влечет Q», или «Р достаточно для Q», или «Q необходимо для Р».
Рассмотрим высказывание «если Р, то Q». В том случае, когда предпосылка Р истинна, мы» src=»https://present5.com/presentacii/20170505/23-razdel_2_logika_i_dokazatelystvo.ppt_images/23-razdel_2_logika_i_dokazatelystvo.ppt_23.jpg» alt=»>Рассмотрим высказывание «если Р, то Q». В том случае, когда предпосылка Р истинна, мы» /> Рассмотрим высказывание «если Р, то Q». В том случае, когда предпосылка Р истинна, мы не можем получить логически корректного заключения, если Q ложно. Однако если посылка Р ложна, мы имеем логически корректное высказывание и когда Q ложно, и когда оно истинно.
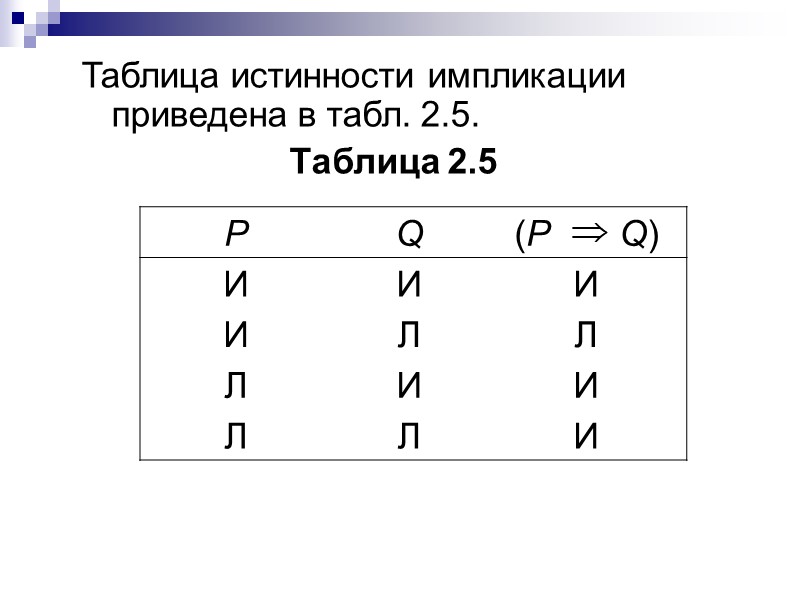
Таблица истинности импликации приведена в табл. 2.5. Таблица 2.5″ src=»https://present5.com/presentacii/20170505/23-razdel_2_logika_i_dokazatelystvo.ppt_images/23-razdel_2_logika_i_dokazatelystvo.ppt_24.jpg» alt=»>Таблица истинности импликации приведена в табл. 2.5. Таблица 2.5″ /> Таблица истинности импликации приведена в табл. 2.5. Таблица 2.5
Пример 2.4. Пусть Р — (ложное) высказывание 1 = 5, Q — (тоже ложное)» src=»https://present5.com/presentacii/20170505/23-razdel_2_logika_i_dokazatelystvo.ppt_images/23-razdel_2_logika_i_dokazatelystvo.ppt_25.jpg» alt=»>Пример 2.4. Пусть Р — (ложное) высказывание 1 = 5, Q — (тоже ложное)» /> Пример 2.4. Пусть Р — (ложное) высказывание 1 = 5, Q — (тоже ложное) высказывание 3 = 7 и R — (истинное) утверждение 4 = 4. Показать, что условные высказывания: «если Р, то Q» и «если Р, то R», — оба истинны.
Решение. Если 1 = 5, то, прибавляя 2 к обеим частям равенства, мы получим,» src=»https://present5.com/presentacii/20170505/23-razdel_2_logika_i_dokazatelystvo.ppt_images/23-razdel_2_logika_i_dokazatelystvo.ppt_26.jpg» alt=»>Решение. Если 1 = 5, то, прибавляя 2 к обеим частям равенства, мы получим,» /> Решение. Если 1 = 5, то, прибавляя 2 к обеим частям равенства, мы получим, что 3 = 7. Следовательно, высказывание «если Р, то Q» справедливо («если Р = Л, то Q = Л»). Вычтем теперь из обеих частей соотношения 1 = 5 число 3 и придем к — 2 = 2. Поэтому, возведя в квадрат: (-2)2 = 22, получим 4 = 4. Таким образом, высказывание «если Р, то R» тоже верно.
Пример 2.5. Высказывание ((не Q) (не Р)) называется противоположным или» src=»https://present5.com/presentacii/20170505/23-razdel_2_logika_i_dokazatelystvo.ppt_images/23-razdel_2_logika_i_dokazatelystvo.ppt_27.jpg» alt=»>Пример 2.5. Высказывание ((не Q) (не Р)) называется противоположным или» /> Пример 2.5. Высказывание ((не Q) (не Р)) называется противоположным или контрапозитивным к высказыванию (Р Q). Показать, что ((не Q) (не Р)) логически эквивалентно высказыванию (Р Q).
Решение. Рассмотрим совместную таблицу истинности Таблица 2.6″ src=»https://present5.com/presentacii/20170505/23-razdel_2_logika_i_dokazatelystvo.ppt_images/23-razdel_2_logika_i_dokazatelystvo.ppt_28.jpg» alt=»>Решение. Рассмотрим совместную таблицу истинности Таблица 2.6″ /> Решение. Рассмотрим совместную таблицу истинности Таблица 2.6
Поскольку два последних столбца этой таблицы совпадают, то и высказывания, о которых идет речь,» src=»https://present5.com/presentacii/20170505/23-razdel_2_logika_i_dokazatelystvo.ppt_images/23-razdel_2_logika_i_dokazatelystvo.ppt_29.jpg» alt=»>Поскольку два последних столбца этой таблицы совпадают, то и высказывания, о которых идет речь,» /> Поскольку два последних столбца этой таблицы совпадают, то и высказывания, о которых идет речь, логически эквивалентны.
Предикаты и кванторы Логика высказываний применяется к простым декларативным высказываниям, где базисные высказывания» src=»https://present5.com/presentacii/20170505/23-razdel_2_logika_i_dokazatelystvo.ppt_images/23-razdel_2_logika_i_dokazatelystvo.ppt_30.jpg» alt=»>Предикаты и кванторы Логика высказываний применяется к простым декларативным высказываниям, где базисные высказывания» /> Предикаты и кванторы Логика высказываний применяется к простым декларативным высказываниям, где базисные высказывания — либо истинны, либо ложны. Утверждения, содержащие одну и более переменных, могут быть верными при некоторых значениях переменных и ложными при других.
Предикатом называется утверждение, содержащее переменные, принимающее значение истины или лжи в зависимости от значений» src=»https://present5.com/presentacii/20170505/23-razdel_2_logika_i_dokazatelystvo.ppt_images/23-razdel_2_logika_i_dokazatelystvo.ppt_31.jpg» alt=»>Предикатом называется утверждение, содержащее переменные, принимающее значение истины или лжи в зависимости от значений» /> Предикатом называется утверждение, содержащее переменные, принимающее значение истины или лжи в зависимости от значений переменных. Например, выражение «x — целое число, удовлетворяющее соотношению x = x2» является предикатом, поскольку оно истинно при x = 0 или x = 1 и ложно в любом другом случае.
Логические операции можно применять и к предикатам. » src=»https://present5.com/presentacii/20170505/23-razdel_2_logika_i_dokazatelystvo.ppt_images/23-razdel_2_logika_i_dokazatelystvo.ppt_32.jpg» alt=»>Логические операции можно применять и к предикатам. » /> Логические операции можно применять и к предикатам. В общем случае истинность составного предиката в конечном счете зависит от значений входящих в него переменных. Однако существуют некоторые, еще незнакомые вам пока логические операторы, называемые кванторами, применение которых к предикатам превращает их в ложные или истинные высказывания.
Пример 2.6. Какие из следующих высказываний истинны, а какие ложны? (а) Сумма внутренних углов» src=»https://present5.com/presentacii/20170505/23-razdel_2_logika_i_dokazatelystvo.ppt_images/23-razdel_2_logika_i_dokazatelystvo.ppt_33.jpg» alt=»>Пример 2.6. Какие из следующих высказываний истинны, а какие ложны? (а) Сумма внутренних углов» /> Пример 2.6. Какие из следующих высказываний истинны, а какие ложны? (а) Сумма внутренних углов любого треугольника равна 180°. (б) У всех кошек есть хвост. (в) Найдется целое число x, удовлетворяющее соотношению х2=2. (г) Существует простое четное число.
Решение: (а) Истинно. (б) Ложно. У бесхвостой кошки хвоста нет. (в) Ложно. (г) Истинно.» src=»https://present5.com/presentacii/20170505/23-razdel_2_logika_i_dokazatelystvo.ppt_images/23-razdel_2_logika_i_dokazatelystvo.ppt_34.jpg» alt=»>Решение: (а) Истинно. (б) Ложно. У бесхвостой кошки хвоста нет. (в) Ложно. (г) Истинно.» /> Решение: (а) Истинно. (б) Ложно. У бесхвостой кошки хвоста нет. (в) Ложно. (г) Истинно. Число 2 является и простым, и четным.
В примере 2.6 мы имеем дело с набором объектов и утверждениями о том, что» src=»https://present5.com/presentacii/20170505/23-razdel_2_logika_i_dokazatelystvo.ppt_images/23-razdel_2_logika_i_dokazatelystvo.ppt_35.jpg» alt=»>В примере 2.6 мы имеем дело с набором объектов и утверждениями о том, что» /> В примере 2.6 мы имеем дело с набором объектов и утверждениями о том, что некоторое свойство имеет место для всех рассматриваемых объектов, или что найдется (существует) по крайней мере, один объект, обладающий данным свойством.
Выражения «для всех» и «найдется» («существует») называются кванторами и обозначаются, соответственно, («перевернутое А») и» src=»https://present5.com/presentacii/20170505/23-razdel_2_logika_i_dokazatelystvo.ppt_images/23-razdel_2_logika_i_dokazatelystvo.ppt_36.jpg» alt=»>Выражения «для всех» и «найдется» («существует») называются кванторами и обозначаются, соответственно, («перевернутое А») и» /> Выражения «для всех» и «найдется» («существует») называются кванторами и обозначаются, соответственно, («перевернутое А») и « » . Включая в предикат кванторы, мы превращаем его в высказывание. Поэтому предикат с кванторами может быть истинным или ложным.
Пример 2.7. Обозначим через Р(x) предикат «x — целое число и х2 = 16».» src=»https://present5.com/presentacii/20170505/23-razdel_2_logika_i_dokazatelystvo.ppt_images/23-razdel_2_logika_i_dokazatelystvo.ppt_37.jpg» alt=»>Пример 2.7. Обозначим через Р(x) предикат «x — целое число и х2 = 16».» /> Пример 2.7. Обозначим через Р(x) предикат «x — целое число и х2 = 16». Выразите словами высказывание: x: Р(x) и определите его истинностное значение. Решение. Высказывание x: Р(x) означает, что найдется целое число x, удовлетворяющее уравнению х2 = 16. Высказывание, конечно, истинно, поскольку уравнение х2 = 16 превращается в верное тождество при x = 4. Кроме того, х = -4 — также решение данного уравнения. Однако нам не требуется рассуждать о знаке переменной x, чтобы проверить истинность высказывания x: Р(x).
Пример 2.8. Пусть Р(x) — предикат: «x — вещественное число и х2 + 1″ src=»https://present5.com/presentacii/20170505/23-razdel_2_logika_i_dokazatelystvo.ppt_images/23-razdel_2_logika_i_dokazatelystvo.ppt_38.jpg» alt=»>Пример 2.8. Пусть Р(x) — предикат: «x — вещественное число и х2 + 1″ /> Пример 2.8. Пусть Р(x) — предикат: «x — вещественное число и х2 + 1 = 0». Выразите словами высказывание: x: Р(x) и определите его истинностное значение. Решение. Данное высказывание можно прочитать так: существует вещественное число x, удовлетворяющее уравнению х2 + 1 = 0. Поскольку квадрат любого вещественного числа неотрицателен, т. е. х2 ≥ 0, мы получаем, что х2 + 1 ≥ 1. Следовательно, утверждение x: Р(x) ложно.
Отрицание высказывания из примера 2.8 записывается в следующем виде: » src=»https://present5.com/presentacii/20170505/23-razdel_2_logika_i_dokazatelystvo.ppt_images/23-razdel_2_logika_i_dokazatelystvo.ppt_39.jpg» alt=»>Отрицание высказывания из примера 2.8 записывается в следующем виде: » /> Отрицание высказывания из примера 2.8 записывается в следующем виде: не x: Р(x). Это, естественно, истинное высказывание, которое означает, что не существует вещественного числа x, удовлетворяющего условию х2 + 1 = 0. Иными словами, каково бы ни было вещественное x, х2 + 1 ≠ 0. В символьной форме это можно записать как x не Р(x).
Для общего предиката Р(x) есть следующие логические эквивалентности: не » src=»https://present5.com/presentacii/20170505/23-razdel_2_logika_i_dokazatelystvo.ppt_images/23-razdel_2_logika_i_dokazatelystvo.ppt_40.jpg» alt=»>Для общего предиката Р(x) есть следующие логические эквивалентности: не » /> Для общего предиката Р(x) есть следующие логические эквивалентности: не x: Р(х) x не Р(х); не x Р(х) x: Р(х). Знак обозначает в символьной форме логически эквивалентные высказывания. Как показывает следующий пример, некоторые трудности возникают, когда в высказывании участвует более одного квантора.
Пример 2.9. Предположим, что x и у — вещественные числа, а Р(x, у) обозначает» src=»https://present5.com/presentacii/20170505/23-razdel_2_logika_i_dokazatelystvo.ppt_images/23-razdel_2_logika_i_dokazatelystvo.ppt_41.jpg» alt=»>Пример 2.9. Предположим, что x и у — вещественные числа, а Р(x, у) обозначает» /> Пример 2.9. Предположим, что x и у — вещественные числа, а Р(x, у) обозначает предикат x + у = 0. Выразите каждое из высказываний словами и определите их истинность. (а) x у : P(x, у); (б) у : x P(x, y).
Решение. (а) Высказывание x у: Р(x, у) говорит» src=»https://present5.com/presentacii/20170505/23-razdel_2_logika_i_dokazatelystvo.ppt_images/23-razdel_2_logika_i_dokazatelystvo.ppt_42.jpg» alt=»>Решение. (а) Высказывание x у: Р(x, у) говорит» /> Решение. (а) Высказывание x у: Р(x, у) говорит о том, что для любого вещественного числа x найдется такое вещественное число у, что x + у = 0. Оно, очевидно, верно, поскольку какое бы число x мы ни взяли, число у = -x обращает равенство x + у = 0 в верное тождество.
(б) Высказывание у: x Р(x, у) читается следующим» src=»https://present5.com/presentacii/20170505/23-razdel_2_logika_i_dokazatelystvo.ppt_images/23-razdel_2_logika_i_dokazatelystvo.ppt_43.jpg» alt=»>(б) Высказывание у: x Р(x, у) читается следующим» /> (б) Высказывание у: x Р(x, у) читается следующим образом: существует такое вещественное число у, что для любого вещественного числа x выполнено равенство x + у = 0. Это, конечно, не так: не существует вещественного числа у, обладающего указанным свойством. Следовательно, высказывание ложно.
Методы доказательств При доказательстве теорем применяется логическая аргументация. Доказательства в» src=»https://present5.com/presentacii/20170505/23-razdel_2_logika_i_dokazatelystvo.ppt_images/23-razdel_2_logika_i_dokazatelystvo.ppt_44.jpg» alt=»>Методы доказательств При доказательстве теорем применяется логическая аргументация. Доказательства в» /> Методы доказательств При доказательстве теорем применяется логическая аргументация. Доказательства в информатике — неотъемлемая часть проверки корректности алгоритмов. Необходимость доказательства возникает, когда нам нужно установить истинность высказывания вида (Р Q). Существует несколько стандартных типов доказательств, включающих следующие:
Прямое рассуждение Предполагаем, что высказывание Р истинно и показываем справедливость Q. Такой» src=»https://present5.com/presentacii/20170505/23-razdel_2_logika_i_dokazatelystvo.ppt_images/23-razdel_2_logika_i_dokazatelystvo.ppt_45.jpg» alt=»>Прямое рассуждение Предполагаем, что высказывание Р истинно и показываем справедливость Q. Такой» /> Прямое рассуждение Предполагаем, что высказывание Р истинно и показываем справедливость Q. Такой способ доказательства исключает ситуацию, когда Р истинно, a Q — ложно, поскольку именно в этом и только в этом случае импликация (Р Q) принимает ложное значение.
Обратное рассуждение Предполагаем, что высказывание Q ложно и показываем ошибочность Р. То» src=»https://present5.com/presentacii/20170505/23-razdel_2_logika_i_dokazatelystvo.ppt_images/23-razdel_2_logika_i_dokazatelystvo.ppt_46.jpg» alt=»>Обратное рассуждение Предполагаем, что высказывание Q ложно и показываем ошибочность Р. То» /> Обратное рассуждение Предполагаем, что высказывание Q ложно и показываем ошибочность Р. То есть, фактически, прямым способом проверяем истинность импликации ((не Q) (не Р)), что согласно примеру 2.5, логически эквивалентно истинности исходного утверждения (Р Q).
Метод «от противного» Предположив, что высказывание Р истинно, a Q ложно, используя» src=»https://present5.com/presentacii/20170505/23-razdel_2_logika_i_dokazatelystvo.ppt_images/23-razdel_2_logika_i_dokazatelystvo.ppt_47.jpg» alt=»>Метод «от противного» Предположив, что высказывание Р истинно, a Q ложно, используя» /> Метод «от противного» Предположив, что высказывание Р истинно, a Q ложно, используя аргументированное рассуждение, получаем противоречие. Этот способ опять-таки основан на том, что импликация (Р Q) принимает ложное значение только тогда, когда Р истинно, a Q ложно.
Пример 2.10. Покажите прямым способом рассуждений, что произведение xу двух нечетных целых чисел x» src=»https://present5.com/presentacii/20170505/23-razdel_2_logika_i_dokazatelystvo.ppt_images/23-razdel_2_logika_i_dokazatelystvo.ppt_48.jpg» alt=»>Пример 2.10. Покажите прямым способом рассуждений, что произведение xу двух нечетных целых чисел x» /> Пример 2.10. Покажите прямым способом рассуждений, что произведение xу двух нечетных целых чисел x и у всегда нечетно. Решение. Прежде всего заметим, что любое нечетное число, и в частности x, можно записать в виде x = 2т + 1, где т — целое число. Аналогично, у = 2n + 1 с некоторым целым n. Значит, произведение xу = (2m + 1)(2n + 1) = 4mn + 2m + 2n + 1 = 2(2mn + m + n) + 1 тоже является нечетным числом.
Пример 2.11. Пусть n — натуральное число. Покажите, используя обратный способ доказательства, что если» src=»https://present5.com/presentacii/20170505/23-razdel_2_logika_i_dokazatelystvo.ppt_images/23-razdel_2_logika_i_dokazatelystvo.ppt_49.jpg» alt=»>Пример 2.11. Пусть n — натуральное число. Покажите, используя обратный способ доказательства, что если» /> Пример 2.11. Пусть n — натуральное число. Покажите, используя обратный способ доказательства, что если n2 нечетно, то и n нечетно. Решение. Отрицанием высказывания о нечетности числа n2 служит утверждение «n2 четно», а высказывание о четности n является отрицанием утверждения «число n нечетно». Таким образом, нам нужно показать прямым способом рассуждений, что четность числа n влечет четность его квадрата n2. Так как n четно, то n = 2т для какого-то целого числа т. Следовательно, n2 = 4m2 = 2(2m2) — четное число.
Пример 2.12. Методом «от противного» покажите, что решение уравнения х2 = 2 является иррациональным» src=»https://present5.com/presentacii/20170505/23-razdel_2_logika_i_dokazatelystvo.ppt_images/23-razdel_2_logika_i_dokazatelystvo.ppt_50.jpg» alt=»>Пример 2.12. Методом «от противного» покажите, что решение уравнения х2 = 2 является иррациональным» /> Пример 2.12. Методом «от противного» покажите, что решение уравнения х2 = 2 является иррациональным числом, т. е. не может быть записано в виде дроби с целыми числителем и знаменателем. Решение. Здесь нам следует допустить, что решение x уравнения x2 = 2 рационально, т. е. записывается в виде дроби x = m/n с целыми m и n, причем n 0. Предположив это, нам необходимо получить противоречие либо с предположением, либо с каким-то ранее доказанным фактом.
Как известно, рациональное число неоднозначно записывается в виде дроби. Например, » src=»https://present5.com/presentacii/20170505/23-razdel_2_logika_i_dokazatelystvo.ppt_images/23-razdel_2_logika_i_dokazatelystvo.ppt_51.jpg» alt=»>Как известно, рациональное число неоднозначно записывается в виде дроби. Например, » /> Как известно, рациональное число неоднозначно записывается в виде дроби. Например, и т.д. Однако можно считать, что т и n не имеют общих делителей. В этом случае неоднозначность записи пропадает.
Итак, предполагаем дополнительно, что дробь x = » src=»https://present5.com/presentacii/20170505/23-razdel_2_logika_i_dokazatelystvo.ppt_images/23-razdel_2_logika_i_dokazatelystvo.ppt_52.jpg» alt=»>Итак, предполагаем дополнительно, что дробь x = » /> Итак, предполагаем дополнительно, что дробь x = несократима (т и n не имеют общих делителей). По условию число x удовлетворяет уравнению х2 = 2. Значит, = 2, откуда т2 = 2n2.
Из последнего равенства следует, что число т2 четно. Следовательно, т тоже четно и может» src=»https://present5.com/presentacii/20170505/23-razdel_2_logika_i_dokazatelystvo.ppt_images/23-razdel_2_logika_i_dokazatelystvo.ppt_53.jpg» alt=»>Из последнего равенства следует, что число т2 четно. Следовательно, т тоже четно и может» /> Из последнего равенства следует, что число т2 четно. Следовательно, т тоже четно и может быть представлено в виде т = 2р для какого-то целого числа р. Подставив эту информацию в равенство т2 = 2n2, мы получим, что 4р2 = 2n2, т. е. n2 = 2р2. Но тогда n тоже является четным числом. Таким образом, мы показали, что как m, так и n — четные числа. Поэтому они обладают общим делителем 2. Если же теперь вспомнить, что мы предполагали отсутствие общего делителя у числителя и знаменателя дроби , то увидим явное противоречие.
Найденное противоречие приводит нас к однозначному выводу: решение уравнения х2 = 2 не может» src=»https://present5.com/presentacii/20170505/23-razdel_2_logika_i_dokazatelystvo.ppt_images/23-razdel_2_logika_i_dokazatelystvo.ppt_54.jpg» alt=»>Найденное противоречие приводит нас к однозначному выводу: решение уравнения х2 = 2 не может» /> Найденное противоречие приводит нас к однозначному выводу: решение уравнения х2 = 2 не может быть рациональным числом, т. е. оно иррационально.
Математическая индукция Компьютерную программу в информатике называют правильной или корректной, если она делает» src=»https://present5.com/presentacii/20170505/23-razdel_2_logika_i_dokazatelystvo.ppt_images/23-razdel_2_logika_i_dokazatelystvo.ppt_55.jpg» alt=»>Математическая индукция Компьютерную программу в информатике называют правильной или корректной, если она делает» /> Математическая индукция Компьютерную программу в информатике называют правильной или корректной, если она делает то, что указано в ее спецификации. Несмотря на то, что тестирование программы может давать ожидаемый результат в случае каких-то отдельных начальных данных, необходимо доказать приемами формальной логики, что правильные выходные данные будут получаться при любых вводимых начальных значениях. О доказательствах такого сорта будет рассказано ниже.
Проверка корректности алгоритма, содержащего циклы, нуждается в довольно мощном методе доказательства, который называется «математическая» src=»https://present5.com/presentacii/20170505/23-razdel_2_logika_i_dokazatelystvo.ppt_images/23-razdel_2_logika_i_dokazatelystvo.ppt_56.jpg» alt=»>Проверка корректности алгоритма, содержащего циклы, нуждается в довольно мощном методе доказательства, который называется «математическая» /> Проверка корректности алгоритма, содержащего циклы, нуждается в довольно мощном методе доказательства, который называется «математическая индукция». Продемонстрируем преимущества этого важного метода, доказав корректность следующего рекуррентного алгоритма, определяющего максимальный элемент из набора a1, a2, a3, …, an натуральных чисел.
begin i := 0; М := 0; while i begin i := 0; М := 0; while i begin i := 0; М := 0; while i Действие алгоритма на наборе данных: а1 = 4, а2 = 7, а3 = 3″ /> Действие алгоритма на наборе данных: а1 = 4, а2 = 7, а3 = 3 и а4 = 8 прослежено в табл. 2.7. Таблица 2.7
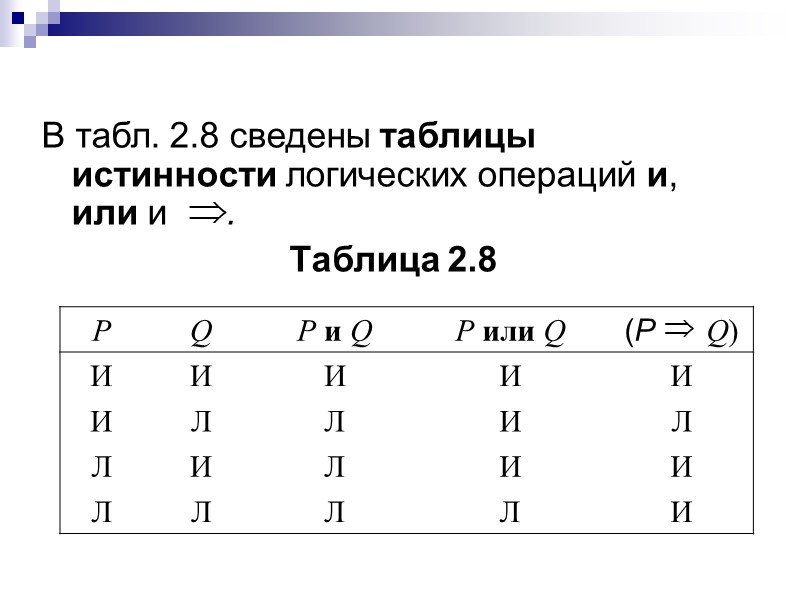
http://math4school.ru/uravnenija_v_celih_chislah.html
http://present5.com/logika-i-dokazatelstvo-vvedenie-v-razdel-logika-neobxodima/