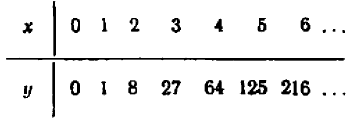
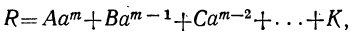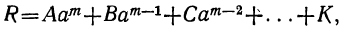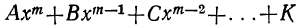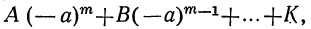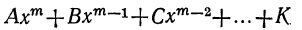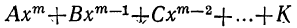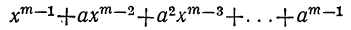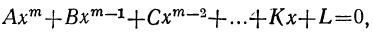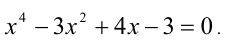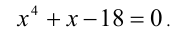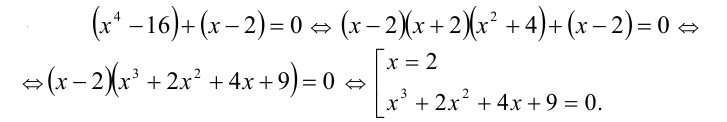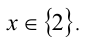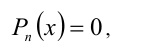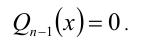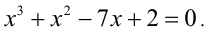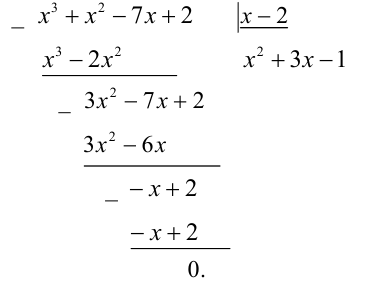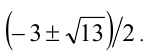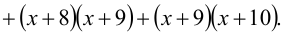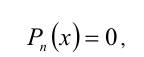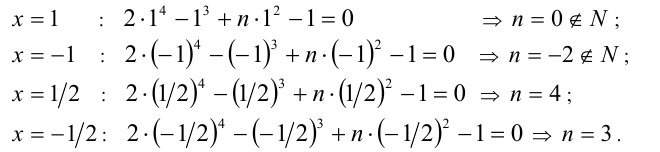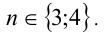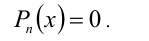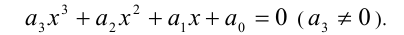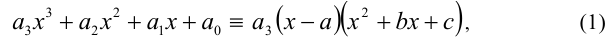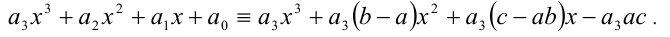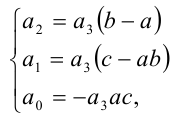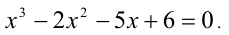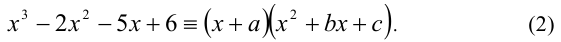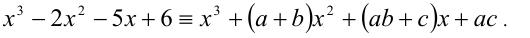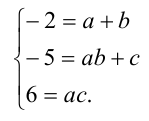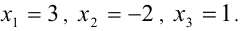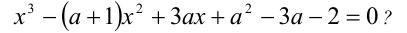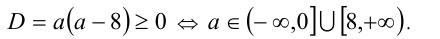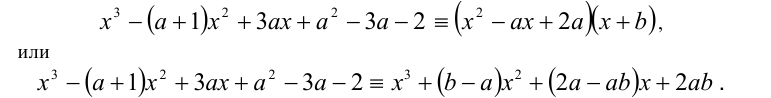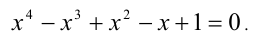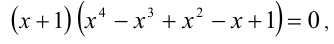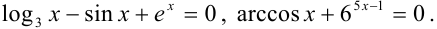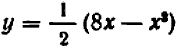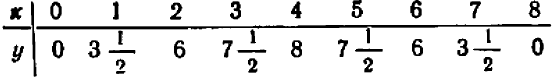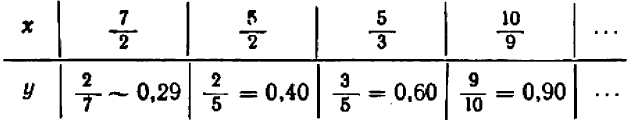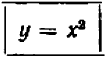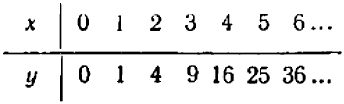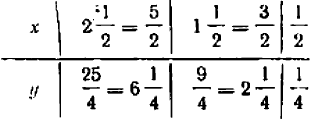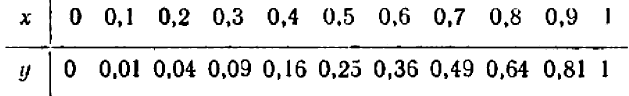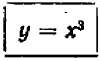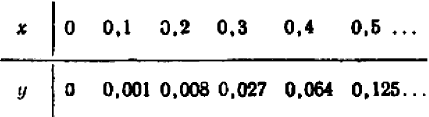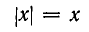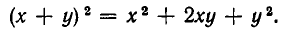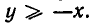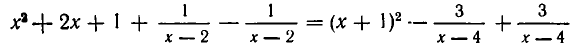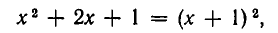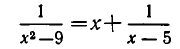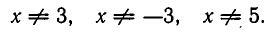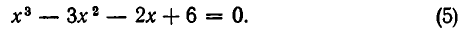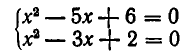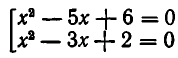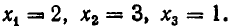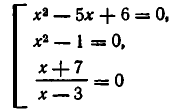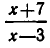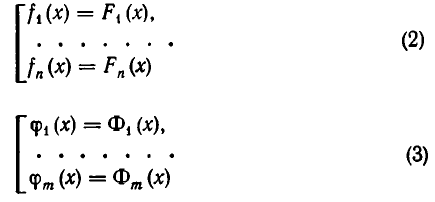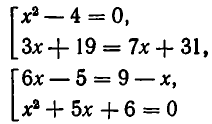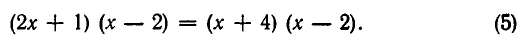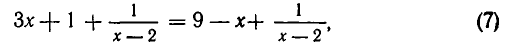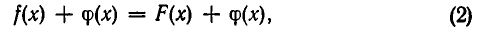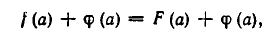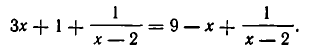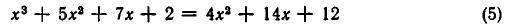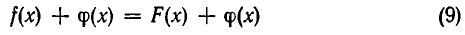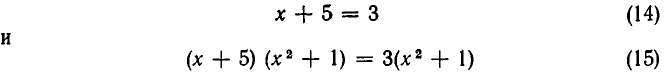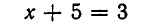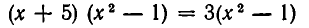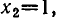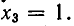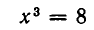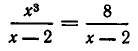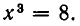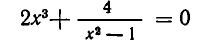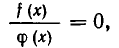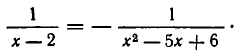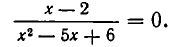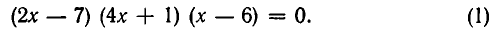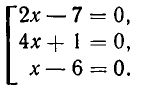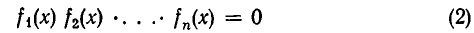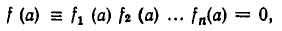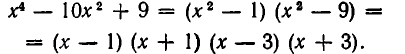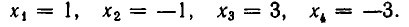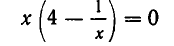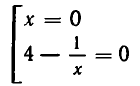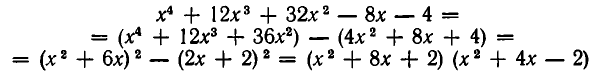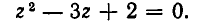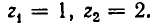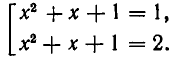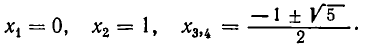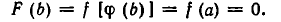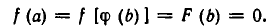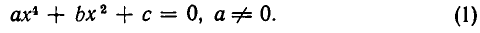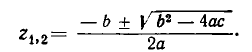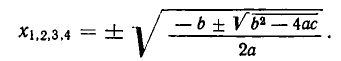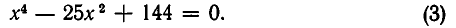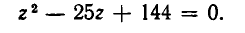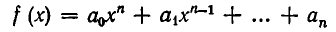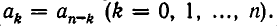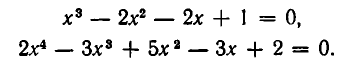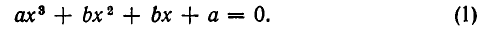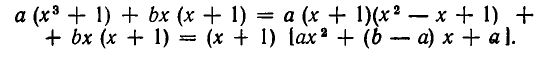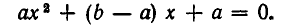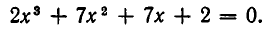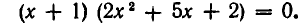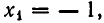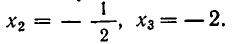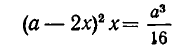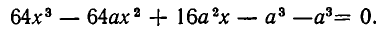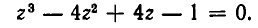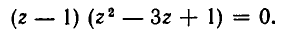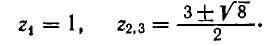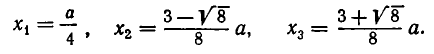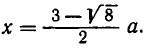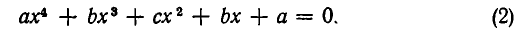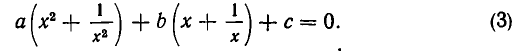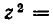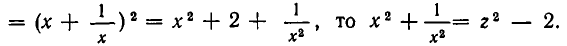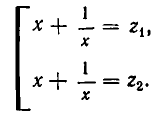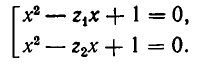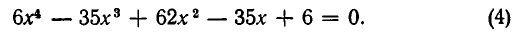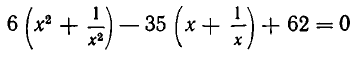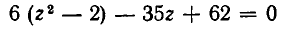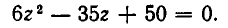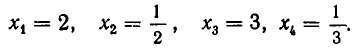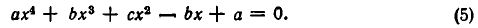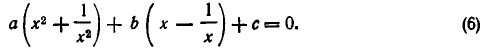Алгебраические уравнения
учитель МБОУ СОШ №12 г. Дзержинска Нижегородской обл.
Тема 1 Алгебраические уравнения
«Мне приходится делить время между политикой и уравнениями. Однако уравнения, по-моему гораздо важнее. Политика существует только для данного момента, а уравнения будут существовать вечно»
Истоки алгебры. Геометрия древних греков. Решение квадратных уравнений.
Решение квадратных уравнений заменой.
Математика как наука появляется тогда, когда начинает свое существование некая достаточно богатая совокупность математических теорий.
Формирование математической науки происходило в научном творчестве ученых Древней Греции. Это группа государств, сложившихся начиная с VIII – VI в. до н. э. на территории современной Греции, близлежащего побережья Малой Азии и юга Италии. Эти государства со временем приобрели вид отдельных самоуправляющихся городов (полисов). Расположенные на самых оживленных в ту пору торговых путях, они приобретали большое экономическое могущество, превратившись к V в. до н. э. в политический, экономический и культурный центр античного мира.
В ряде ранних источников содержатся высказывания, говорящие о преемственности математических и вообще математических знаний. Так, в них упоминается о поездках купцов и образованных граждан древнегреческих полисов в другие страны. Чаще других речь идет о Египте и иных странах ближнего Востока, о развитии в них науки и о технических достижениях. Практический характер математики и успехи её в этих странах были высоко оценены и восприняты полностью.
В течении долгого времени математические сведения не были выделены в отдельную область науки. Важные и интересные астрономические, технические и другие открытия, наблюдения за явлениями природы, новые методы вычислений и решения новых классов задач стекались в Грецию со всех сторон, распространялись в кругах образованных людей, сливаясь в единую, хотя и слабо поначалу объединенную, область всеобщего научного знания. Называли эту область – матема (μ α τ η μ α ) – «знание, наука». Факты этой науки приобретали название научных, математических.
Но время шло, и постепенное накопление научных сведений объективно вынуждало к тому, чтобы их упорядочить, классифицировать. То же стремление к разделению, дифференциации знаний вырастало из практики школьного обучения. Известно, что дети свободных граждан рабовладельческих Афин и других полисов с 7-летнего возраста учились в школах. Там их обучали как дисциплинам практического назначения, так и началам теоретического научного знания, в том числе основам теоретической арифметики и геометрии. Став взрослыми, они вследствие привилегированного положения в обществе передавали подневольным людям не только физический труд, но и решение практических задач, связанных с необходимостью счета и измерений.
Такое разделение математических занятий, возникшее в силу социального неравенства, ускоряло объективное течение исторического процесса дифференциации научных знаний и выделение слоя людей, занимающихся теоретическими проблемами математики.
Этому же способствовала деятельность учебно-научных объединений натурфилософского направления (научных школ).
2. Геометрия древних греков.
Самые ранние научные школы:
1) ионийская (VII – VI в. до н. э. в островной части Греции)
2) пифагорейская ( VI – V в. до н. э. в южной части Аппенинского полуострова)
В IV в. до н. э. в материковой части Греции функционировали школы, среди которых выделялись:
· Лицей Аристотеля, учителя Александра Македонского.
Это были небольшие группы людей, собиравшихся вокруг известных ученых; преподавание велось главным образом устно.
Одним из самых первых шагов в направлении дифференциации содержания математики явилось отделение области практических навыков и сведений Эта область математики получила особое название логистика, в логистику входили:
· счет (арифметические действия над натуральными числами с применением счетной доски– абака);
· действия с дробями;
· вычисления корней, по преимуществу квадратных;
· решение разнородных типов задач приемами, известными из учебников арифметики.
Уже в школе Пифагора заметен процесс накопления абстрактных математических фактов, соединения их в теоретические системы.
1) Из арифметики была выделена в отдельную область исследований теория операций с натуральными числами.
2) Начались абстрагирование и систематизация геометрических сведений. Самым ранним сочинением по систематизации геометрии являются «Начала» Гиппократа (V в. до н. э.) с острова Хиос.
3) Открытие иррациональностей. Самой первой иррациональностью было число
После открытия иррациональностей оказалось, что множество геометрических величин (например, отрезков прямой) более полно, чем множество рациональных чисел и целесообразно более общее исчисление строить в геометрической форме. Новое исчисление было создано, мы его знаем под названием геометрической алгебры.
Первичными элементами геометрической алгебры являлись отрезки. Операции с ними:
1) сложение – приставление отрезков друг к другу;
2) вычитание – отбрасывание от отрезка части;
3) умножение а и в – построение прямоугольника со сторонами а и в; если дается 3 отрезка в произведении, то получается параллелепипед, произведение большего числа множителей не рассматривалось;
4) деление – интерпретировалось эквивалентной задачей приложения площадей (при условии, что размерность делимого больше размерности делителя).

Решение состоит в прикладыванию друг к другу прямоугольников (ав) и (вс) и в построении нового прямоугольника, диагональю которого является диагональ прямоугольника (вс), продолженная до пересечения с продолжением стороны в. Тогда прямоугольники (ав) и (сх) оказываются равновеликими.
Метод приложения площадей позволял решать задачи, сводящиеся к линейным уравнениям и носил название параболического, что в переводе с греческого означает «приложение». При решении задач с помощью методов геометрической алгебры получали в результате только положительные решения. Это обстоятельство выявляло ограниченность области применения методом геометрической алгебры. Еще больше ограничений возникало из-за того, что её объектами оказывались образы размерности не выше второго, т. к. средствами построения были только циркуль и линейка. С помощью циркуля и линейки можно решать задачи, эквивалентные квадратным уравнениям, имеющим действительный положительный корень. Оказалось, что существует целый класс задач, не поддающихся решению с помощью циркуля и линейки. Среди них:
Этим была особенно подчеркнута недостаточность геометрической алгебры для того, чтобы играть роль общей математической теории.
Алгебра зарождалась и развивалась постепенно в недрах арифметики в связи с задачей решения уравнений. Еще в глубокой древности египтяне, вавилоняне и индийцы владели первоначальными элементами алгебры; они умели по условиям задачи составлять уравнения и решать некоторые из них.
Алгебра вырастала из арифметики, из вычислительной практики людей. Тенденции роста, которые можно отнести к алгебраическим, появились очень рано. Они вначале представляли собой стремление группировать однотипные задачи формулировать, возможно, более общие правила их решения. У них была общая особенность: неизвестное, которое требуется отыскать по условию задачи, получало свое особое название, а затем обозначалось специальным символом. На вавилонских клинописных пластинках и египетских папирусах содержится ряд задач, которые можно решить составлением уравнений. Вавилонские математики 4000 лет назад решали их с помощью специальных таблиц и правил, которыми предписывалась последовательность действий, однако они еще не знали буквенных обозначений величин, и общих приемов решения у них не было. В Древнем Египте при решении таких задач для обозначения такого числа был установлен особый значок, называли его «хау», что в переводе на русский значит «куча»или «все вместе». При решении подобных задач в математике пользовались правилом «ложного положения», или «фальшивым правилом».
В течение всей истории алгебры выделение и обозначение неизвестного было непременным признаком алгебраических суждений. Запись действий, содержащий символ неизвестной, представляет собой по существу уравнение. Элементы алгебры со времен древнегреческой математики, т. е. приблизительно с начала нашего летоисчисления, начали свой исторический путь параллельно в двух формах:
В качестве одного из следствий в алгебре установились и в силу традиций удержались до наших дней геометрически звучащие термины (квадраты, кубы, линейные уравнения и др.) для обозначения чисто алгебраических объектов.
В первые века нашей эры математика наиболее быстро стала развиваться в государствах средневекового Востока. Арабские завоевания привели к распространению языка арабов и их религии – ислама. IX XII века – это расцвет науки в арабоязычных странах: начала складываться научная традиция, основанная на научном наследии, арабский язык становится языком науки.
Выдающийся арабский математик и астроном Абу Мусса аль-Хорезми, то есть отец Абдалаха, Мухаммед, сын Муссы, жил и работал в Багдаде. Аль-Хорезми буквально означает «из Хорезма», т. е. родился в городе Хорезме (сейчас входит в состав Узбекистана). В то время в Багдаде правил халиф аль — Мамун, который уважал ученых и покровительствовал наукам. По его велению в Багдаде был построен Дом мудрости с библиотекой и обсерваторией. Здесь работали почти все крупные арабские ученые, в том числе и аль-Хорезми., который написал трактат «Китаб аль джебр аль-мукабала», что означает «Книга о восстановлении и противопоставлении». В ней решение уравнений рассматривается не в связи с арифметикой, а как самостоятельный раздел математики.
Основополагающим сочинением по алгебре был трактат узбекского математика и астронома IXв. аль-Хорезми. Название трактата в переводе означает: книга об операциях «джебр» (медицинский термин – вправка сломанного члена или перелома; восстановление) и «кабала» (приведение) Первая из операций, из названия которой получилось название всей алгебры, состоит в переносе членов уравнения с одной стороны знака равенства в другую.
«Аль-джебр» При решении уравненья,
Если в части одной,
Безразлично в какой,
Встретился член отрицательный,
Мы к обеим частям,
С этим членом сличив,
Равный член придадим,
Только с знаком другим,-
И найдем результат, нам
Вторая операция является приведением подобных членов в уравнении.
«Аль-мукабала» Дальше смотрим в уравненье,
Можно сделать приведенье,
Если члены есть подобны,
Сопоставьте их удобно.
Вычитая равный член из них,
К одному приводим их.
Решение уравнений у аль-Хорезми рассматривается не в связи с арифметикой, а как отдельная наука. Так как в те времена отрицательные числа считались ненастоящими, то действие «аль-джебр» как бы превращающее число из небытия в бытие, казалось чудом. Эту науку в Европе долго считали «великим искусством», рядом с «малым искусством» — арифметикой. Термин «алгебра», как название искусства восстановления, у арабов перешел и в медицину. Выправление кости сломанной руки или ноги также являлось восстановлением поврежденного органа, и искусство врача, возвращающее человеку работоспособность руки или ноги, также стали называть алгеброй.
Двойной смысл слова «алгебра» объясняет нам странный, на первый взгляд, факт. В известном романе Сервантеса рассказывается, как Дон Кихот сбил с лошади своего противника, как тот лежал на земле, не в силах пошевелить ни ногой, ни рукой, и как Дон Кихоту удалось найти алгебраиста для оказания помощи побежденному противнику. В более поздних изданиях слово «алгебраист» заменено словом «костоправ». (Испанский и португальский языки заимствовали слово «алгебра» из арабского в двух его значениях.)
Алгебраический трактат Мухаммеда аль-Хорезми послужил началом создания алгебры
В трактате содержатся систематические решения уравнений 1 и 2 степени. Автор приводит как арифметические, так и геометрические решения уравнений. Доказательств не было (в те времена доказательства были только в геометрии), способ решения задачи излагался в виде рецептов. Аль-Хорезми один из первых стал обращаться с уравнениями так, как торговец обращается с рычажными весами. Взгляд на уравнение как на равенство грузов на весах, на обеих чашах которых можно производить одинаковые преобразования, оказался очень плодотворным.
В те времена буквенная символика отсутствовала и уравнения записывались словами. Но и в такой «словесной форме» уравнения существенно облегчили решение многих задач. В XII в. «Алгебра» аль-Хорезми стала известна в Европе и была переведена на латинский язык. Книга Хорезми пользовалась большой известностью. Сама книга, долгое время считавшаяся потерянной, была найдена в 1857 г. в библиотеке Кембриджского университета (Великобритания). Точнее, был найден её перевод на латинский язык. Первые строки книги были переведены так: «Сказал Алгоритми. Воздадим хвалу Богу, нашему вождю и защитнику». Термин «алгебра» укоренился в математике, осталось в этой науке и имя автора (аль-Хорезми) в латинизированном виде: «алгоритм». Вначале это слово означало фамилию, затем нумерацию по позиционной системе, а теперь всякую систему вычислений, производимых по строго определенным правилам и заведомо приводимых к решению поставленной задачи.
Алгебраические арабские трактаты IX –XV веков помимо решения уравнений 1 и 2 степеней, включали в себя и кубические уравнения. К ним приводили задачи: рассечение шара плоскостью; трисекция угла; отыскание сторон правильных 7 и 9-угольников.
Численное решение кубических уравнений развивалось, начиная от способа проб Бируни () до изящного итерационного быстро сходящегося метода ал—Каши (15 век). Большой вклад в теорию решения уравнений внесла деятельность среднеазиатского математика Омара Хайяма (11-12 века). Дальнейшее формирование алгебры происходило в странах Европы, где сложилась для этого благоприятная обстановка.
3. Решение квадратных уравнений
Методы решения квадратных уравнений были известны еще в древние времена. Они излагались в вавилонских рукописях царя Хаммурапи (XX в. до н. э.), в трудах древнегреческого математика Евклида (III в. до н. э.), в древних китайских и японских трактатах. Многие математики древности решали квадратные уравнения геометрическим способом. Примеры решения уравнений без обращения к геометрии дает Диофант Александрийский (III в.). В своем трактате Мухаммед аль-Хорезми в 925 г. разъясняет приемы решения квадратных уравнений. После трудов немецкого математика М. Штифеля (), нидерландца А. Жирара (), Р. Декарта и И. Ньютона, способ решения квадратных уравнений принял современный вид. А в 1591 г. Ф. Виет вывел формулы, выражающие зависимость корней квадратного уравнения от его коэффициентов и сформулировал свою знаменитую теорему.
Франсуа Виет () – французский адвокат, ставший советником короля Франции Генриха III, затем Генриха IV. Голландский математик Андриан Ван-Роумен в конце 16 столетия решил бросить вызов всем математикам мира. Он разослал во все европейские страны уравнение 45–й степени: 
Франсуа Виет по существу создал новую алгебру. Он ввел в неё буквенную символику. Основные его идеи изложены в труде «Введение в аналитическое искусство», он писал: «Искусство, которое я излагаю, ново. Все математики знали, что под их алгеброй и аль — мукабалой были скрыты несравненные сокровища, но не умели их найти: задачи, которые они считали наиболее трудными, совершенно легко решаются с помощью нашего искусства».
До Ф. Виета решение каждого квадратного уравнения выполнялось по своим правилам в виде очень длинных словесных рассуждений и описаний, довольно громоздких действий. Даже само уравнение в современном виде не могли записать. Для этого тоже требовалось длинное и сложное словесное описание. На овладение приемами решений уравнений требовались годы. Общих правил, подобных современным, а тем более формул решения уравнений не было. Постоянные коэффициенты буквами не обозначались. Рассматривались выражения только с конкретными числовыми коэффициентами.
Виет ввел в алгебру буквенную символику. После открытия Виета стало возможным записывать правила в виде формул. Правда у Виета показатели степеней ещё обозначались словами, и это создавало определенные трудности в решении некоторых задач. Во времена Виета был ещё ограничен запас чисел. Так, ещё не нашли своего признания отрицательные числа. Франсуа Виет очень подробно изложил в своих трудах теорию решения уравнений с первой по четвертую степень. Виета называют «отцом» алгебры, основоположником буквенной символики.
Большой заслугой Виета было открытие зависимости между корнями и коэффициентами уравнений приведенного вида произвольной натуральной степени. Нам хорошо известна знаменитая теорема Виета для приведенного квадратного уравнения, эта теорема позволяет устно проверять правильность решения квадратных уравнений, а в простейших случаях устно находить и корни уравнений.
По праву достойна в стихах быть воспета
О свойствах корней теорема Виета.
Что лучше, скажи, постоянства такого:
Умножишь ты корни и дробь уж готова:
В числителе с, в знаменателе а.
А сумма корней тоже дроби равна.
Хоть с минусом дробь эта, что за беда-
В числителе в, в знаменателе а.
Само название «квадратные уравнения» было введено сравнительно недавно: в 1710 г. его предложил учитель Ломоносова, немецкий математик Христиан Вольф. В настоящее время известно много способов решения квадратных уравнений. Интересна статья И Плужникова в газете «Математика» № 40 за 2000г. «Десять способов решения квадратных уравнений».
Разложение левой части уравнения на множители. Метод выделения полного квадрата. Решение по формуле с помощью дискриминанта.
( Термин «дискриминант» происходит от лат. discriminantis – разделяющий, различающий.)
Решение уравнений с использованием теоремы Виета. Способ «переброски». С использованием свойств коэффициентов. Графическое решение. Решение с помощью циркуля и линейки. Решение с помощью номограммы из таблиц Брадиса способ аль-Хорезми.
Рассмотрим ещё один способ решения квадратных уравнений – способ замены переменной.
Уравнение 


Например: 
Замена z = 
3 (z – 1)2 + 6 (z – 1) +1 = 0,
3 z2 – 6 z + 3 + 6 z – 6 + 1 = 0,


Ответ. 
«Человеку, изучающему алгебру, часто полезнее решить одну и ту же задачу тремя различными способами, чем решать три-четыре различные задачи. Решая одну задачу различными способами, можно путем сравнения выяснить, какой из них короче и эффективнее. Так вырабатывается опыт.»
В первой половине XVI в. благодаря усилиям итальянских математиков в алгебре происходят крупные сдвиги, сопровождаемые весьма драматическими событиями. В средние века проводились не только рыцарские турниры. Случались и научные поединки, на которых ученые состязались между собой в том, кто быстрее и больше решит задач, предложенных противником. Победитель получал деньги и обретал славу, ему предлагали занять почетную, хорошо оплачиваемую должность. Выделяются своими научными достижениями итальянские математики.
Профессор Болонского университета Сципион Даль Ферро (1465–1526) находит общее решение уравнения третьей степени но держит его в секрете, ибо оно представляет большую ценность на соревнованиях по решению задач, которые тогда широко практиковались в Италии. Перед смертью он открывает секрет своему ученику Фиоре.
В 1535 Фиоре вызывает на соревнование талантливейшего математика Никколо Тарталью (1499–1557), который, зная, что Фиоре обладает способом решения кубического уравнения, прилагает максимум усилий и сам за несколько дней до поединка находит решение! Поединок состоялся 12 февраля 1535 г. Каждому из состязующихся надо было решить по 30 задач. За два часа Тарталья справился со всеми задачами, предложенными ему Фиоре, а тот не решил ни одной задачи противника. Победа была полной!
Тарталья побеждает на соревновании, но также держит свое открытие в секрете. Наконец появляется Джероламо Кардано (1501–1576), который был одновременно математиком и механиком, врачом и алхимиком, хиромантом и личным астрологом римского папы. С юности Джероламо обуревала жажда славы «Цель к которой я стремился, писал он в автобиографии, — заключалась в увековечивании моего имени…» Он тщетно пытается найти алгоритм решения кубического уравнения и в 1539 г. обращается к Тарталье с просьбой поведать ему тайну. Взяв с Кардано «священную клятву» молчания, Тарталья частично и в не слишком вразумительной стихотворной форме приоткрывает для него завесу. Кардано не удовлетворяется и прилагает усилия, чтобы ознакомиться с рукописью покойного Даль Ферро. Это ему удается, и в 1545 г. он публикует книгу, трактат по алгебре под названием «Великое искусство», в которой сообщает алгоритм, сводящий решение кубического уравнения к радикалам («формула Кардано») – секрет Даль Ферро и Тартальи. В этой же книге содержится еще одно открытие, сделанное учеником Кардано Луиджи Феррари (1522–1565), а именно решение в радикалах уравнения четвертой степени. Тарталья обвиняет Кардано в нарушении клятвы, завязывается острая и продолжительная полемика. При таких обстоятельствах заявляет о своих первых существенных достижениях математика Нового времени. Само название «кубическое уравнение» было введено только в 1619 г. французским ученым Рене Декартом.
«Большинство жизненных задач решаются как алгебраические уравнения: приведением их к самому простому виду» писал . И, действительно, решение кубических уравнений часто сводится к решению линейных и квадратных уравнений. Во многих задачах «торчат уши квадратного трехчлена» дает подсказку , обращаясь к абитуриентам.
Определение. Уравнение вида ах3 + вх2 + сх + d = 0, 
Основная теорема алгебры. Всякий многочлен п –й степени в множестве комплексных чисел имеет ровно п корней.
Согласно этой теореме всякое кубическое уравнение имеет три корня в множестве комплексных чисел.
Рассмотрим различные способы решения кубических уравнений:
1. Способ группировки
Рассмотрим решение уравнения 







Д 0, то у1 

2) если Δ = 0, p ≠0 , q ≠0 , то уравнение имеет три действительных корня, два из которых совпадают; при p = q = 0 получаем 3 совпадающих корня у1,2,3 = 0.
3) если Δ 0 , тогда есть один действительный корень х1 = А + В, х1=1 – 5 = — 4, и два комплексно сопряженных 
Ответ. х1 = -5, х2,3 = 2± 3
2) 
p = — 12, q = 16 , 
Δ= 0, тогда уравнение имеет три действительных корня, два из которых совпадают

х1 = -2 + (-2) = — 4 , 
3)
p = -21, q = 20 ,
К алгебраическим уравнениям относятся уравнения которые представляет собой
Ключевые слова: уравнение, алгебраическое уравнение, корень уравнения, линейное уравнение, квадратное уравнение, возвратное уравнение
Типы уравнений
- Алгебраические уравнения. Уравнения вида fn(x) = 0, где fn(x) – многочлен одной переменной, называются алгебраическими уравнениями.
Многочленом называется выражение вида fn(x) = anx n + an-1xn-1 + . + a1x + a0 = 0 - Трансцендентные уравнения. Уравнения, содержащие трансцендентные функции, такие, как логарифмическая, показательная или тригонометрическая функция, называются трансцендентными.
- Дифференциальные уравнения. Так называются уравнения, содержащие одну или несколько функций и их производные или дифференциалы.
Дифференциальные уравнения оказались исключительно ценным средством точной формулировки законов природы.
Например, уравнение 3x – 5y = 1 имеет решение x = 7, y = 4; вообще же его решениями служат целые числа вида x = 7 + 5n, y = 4 + 3n.
Алгебраические уравнения
Линейное уравнение. ax + b = 0
$$(a \ne 0)\Rightarrow x = -\frac$$.
Биквадратное уравнение. ax 4 + bx 2 + c = 0 $$(a \ne 0)$$
Заменой y = x 2 приведем к уравнению ay 2 + by+ c = 0 $$\Rightarrow x_<1>,_<2>= \pm \sqrt<\frac<-b -\sqrt
$$ x_<3>,_<4>= \pm \sqrt<\frac<-b +\sqrt
Возвратное (алгебраическое) уравнение. ax 4 + bx 3 + cx 2 + bx + a = 0 $$(a \ne 0)$$
Заменой $$y = x + \frac<1>
Уравнение четвертой степени общего вида. ax 4 + bx 3 + cx 2 + dx + e = 0 $$(a \ne 0)$$
Двучленное алгебраическое уравнение n-й степени. x n — a = 0 $$\Rightarrow x = \root n \of $$.
Степенное алгебраическое уравнение. ax 2 n + bx n + c = 0 $$(a \ne 0)$$
Заменой y = x n приведем к уравнению ay 2 + by+ c = 0.
Алгебраическое уравнение n-й степени общего вида. anx n + an-1x n-1 + . + a1x + a0 = 0 $$(a \ne 0)$$.
Можно решить по обобщенной теореме Виета $$x_<1>+x_<2>+x_<3>+. + x_
$$x_ <1>\cdot x_ <2>+ x_ <1>\cdot x_ <3>+. + x_
Функция f ( x ) называется рациональной ( дробно-рациональной), если она представима в виде отношения двух многочленов: $$f(x) = \frac
Уравнение f ( x ) = g ( x ) называется дробно-рациональным , если f ( x ) и g ( x ) являются дробно-рациональными функциями.
Алгебраические уравнения в математике с примерами решения и образцами выполнения
Алгебраическое уравнение — это уравнение вида. где. — многочлен от переменных. , которые называются неизвестными.
Делимость многочлена
Делимость многочлена, целого относительно х, на разность x— а.
Теорема Безу:
Многочлен, целый относительно х: 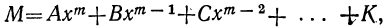
при делении на разность х — а (где а есть произвольное число, положительное или отрицательное) даёт остаток
равный тому значению делимого, которое оно получает при х=а.
Доказательство:
Из процесса деления многочлена, расположенного по убывающим степеням буквы х, видно, что деление такого многочлена на х — а можно продолжать до тех пор, пока высший член остатка R не будет содержать в себе буквы х. Пусть при этом частное будет некоторый многочлен Q. Тогда мы можем написать равенство:
M=(x- a)Q+R.
Равенство это есть тождество, т. е. оно верно при всевозможных значениях буквы х, а потому оно должно быть верно и при х-а. Но при x=а оно даёт
M’ = (α — α) Q’ + R
если буквами М‘ и Q‘ обозначим те значения M и Q, которые эти многочлены принимают при х=а (остаток R, как не содержащий вовсе x, не изменится от подстановки а на место х). Так как a — α=0, то и произведение (а — a) Q‘ равно 0; значит, последнее равенство даёт M‘= R, т. е.
что и требовалось доказать.
Следствие:
Так как x+α=x— (—а), то, применяя доказанную теорему к сумме х+а, найдём:
многочлен
при делении на сумму x+α даёт в остатке число, равное
т. е. число, равное тому значению делимого, которое оно получает при x= —а.
Примеры:
1) Многочлен x⁵—3x²+5x—1 при делении на х—2 даёт остаток, равный
2⁵-3 ∙ 2²+5 ∙ 2—1=29.
2) Многочлен x⁵—3x²+5x—1 при делении на x+2 даёт остаток
(-2)⁵-3 (- 2)²+5 (-2)—1=-55.
Следствие:
Для того чтобы многочлен
делился на разность х—а, необходимо и достаточно, чтобы при х=а он обращался в нуль.
Это необходимо, так как если указанный многочлен делится на x—а, то остаток от деления должен быть нуль, а этот остаток, по доказанному выше, есть то значение делимого, которое оно принимает при x=а. Это и достаточно, так как если многочлен обращается в нуль при x=a, то это значит, что остаток от деления этого многочлена на х—а равен нулю.
Следствие:
Для того чтобы многочлен
делился на сумму х+а, необходимо и достаточно, чтобы при х = —а он обращался в нуль, так как сумма х+а есть разность x—(— а).
Примеры:
1) Многочлен x³-4x²+9 делится на х—3, потому что
З³ — 4∙3²+9=0.
2) Многочлен 2x²+x-45 делится на x+5, так как
2 (-5)²+(-5)—45=0.
Делимость двучлена 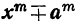
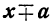
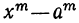
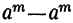
2) Сумма одинаковых степеней двух чисел не делится на разность этих чисел, так как 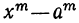
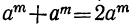
3) Разность одинаковых чётных степеней двух чисел делится, а нечётных не делится на сумму этих чисел, так как при делении разности 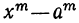
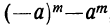
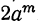
4) Сумма одинаковых нечётных степеней двух чисел делится, а чётных не делится на сумму этих чисел, так как. при делении суммы 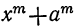
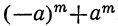
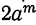
Примеры:
1) x¹+α¹ делится на x+α, но не делится на х—а.
2) x²- α² делится и на х—а, и на x+a.
3) x²+α² не делится ни на х—а, ни на x+a.
4) x³- α³ делится на х—а, но не делится на x+α.
5) x³+α³ делится на x+a, но не делится на х—а.
Частные, получаемые при делении 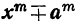
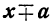
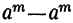
(остатки при этом делении идут в такой последовательности: 1-й остаток 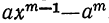
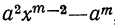
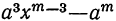
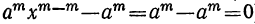
Очевидно, что многочлен, получившийся в частном, содержит m членов; сумма показателей в каждом члене при а и х одна и та же, именно: m—1; показатели х идут, уменьшаясь на 1,от m—1 до 0, показатели же а идут, увеличиваясь на 1, от 0 до m—1; коэффициенты у всех членов равны 1; знаки все +; число членов в частном m.
Заметив это, можем прямо писать:
x³- α³=(x-a) (x²+αx+α²);
x⁴- α⁴=(x-α) (x³+αx²+α²x+ α³);
x⁵ — α⁵=(x-a) (x⁴+αx3+α²x²+α³x+α⁴) и т. п.
Чтобы получить частное от деления 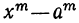
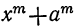
x³+α³=(x+α) (x²-αx+α²);
x⁴—α⁴=(x+α) (х³-αx²+α²x-α³);
x⁵+a⁵=(x+α) (х⁴ — αx³+α²x² — a³x+a⁴) и т.п.
Общий вид алгебраического уравнения
Мы ранее видели, что уравнение, содержащее неизвестное в знаменателях, может быть приведено к целому виду. Далее мы знаем, что уравнение, содержащее неизвестное под знаком радикала, может быть приведено к рациональному виду. Вследствие этого можем сказать, что всякое уравнение, в котором неизвестное связано с данными числами посредством конечного числа шести алгебраических действий (сложения, вычитания, умножения, деления, возвышения в степень и извлечения корня), может быть приведено к такому целому и рациональному виду:
где коэффициенты А, В, С, … , K и L суть постоянные вещественные или комплексные числа, а m есть показатель степени уравнения. Некоторые коэффициенты, кроме первого, в частных случаях могут равняться нулю.
Уравнение такого вида называется алгебраическим. Алгебраические уравнения степени выше второй называются уравнениями высших степеней.
Некоторые свойства алгебраического уравнения
Уравнения высших степеней составляют предмет высшей алгебры. Элементарная же рассматривает только некоторые частные виды этих уравнений.
Высшая алгебра устанавливает следующую важную теорему:
Всякое алгебраическое уравнение имеет вещественный или комплексный корень (теорема Гаусса 2), 1799 г.).
Допустив эту истину (доказательство которой в элементарной алгебре было бы затруднительно), нетрудно показать, что:
Алгебраическое уравнение имеет столько корней, вещественных или комплексных, сколько единиц в показателе его степени.
Действительно, согласно теореме Гаусса, уравнение
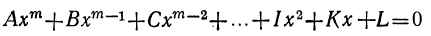
имеет вещественный или комплексный корень; пусть этот корень будет а. Тогда многочлен, стоящий в левой части уравнения (1), должен делиться на х—а. Если произвести это деление, то в частном получим многочлен степени m—1, у которого первый коэффициент будет А. Обозначив другие его коэффициенты соответственно буквами B₁, C₁ ,…, K₁ и приняв во внимание, что делимое равно делителю, умноженному на частное, можем представить уравнение (1) так:
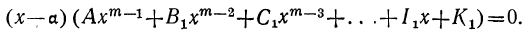
Приравняв нулю многочлен, стоящий во вторых скобках, получим новое уравнение, которое по той же теореме должно иметь некоторый корень β; вследствие этого левая его часть может быть разложена на два множителя: х—β и многочлен степени m—2, у которого первый коэффициент по-прежнему будет А. Поэтому уравнение (1) можно переписать так:
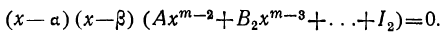
Продолжая эти рассуждения далее, дойдём, наконец, до того, что многочлен, заключённый в последних скобках, будет второй степени, причём первый его коэффициент останется А. Разложив этот трёхчлен на множители, приведём уравнение (1) к виду:
A(x- а) (х—β) (х— γ) . .. (х—λ)=0, (4)
где всех разностей: x-a, х- β,…, будет m. Очевидно, что уравнение (4) обращается в тождество при каждом из значений: x=α, x=β, x=γ, . x=λ и не удовлетворяется никакими иными значениями x (если A≠0); значит, уравнение (1) имеет m корней: a, β, γ ,…, λ. В частных случаях некоторые корни могут оказаться одинаковыми.
Полезно заметить ещё следующие истины, доказываемые в высшей алгебре.
Сумма корней всякого алгебраического уравнения 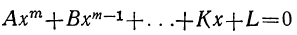
равна 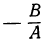
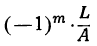
Если алгебраическое уравнение с вещественными коэффициентами имеет комплексные корни, то число этих корней — чётное (примером может служить биквадратное уравнение).
Если алгебраическое уравнение с вещественными коэффициентами имеет n корней вида p+qi, оно имеет ещё n корней вида p—qi (примером может служить биквадратное уравнение, комплексные корни которого всегда сопряжённые), и так как
[х—(p+qi)][x-(р— qi)]=[(x-p)- qi] (x-p)+qi] =
=(х—р)²—q²i²=(x-p)²+q²=x²-2 +(p²+q²),
то левая часть уравнения содержит в этом случае n вещественных множителей вида ax²+bx+c.
Алгебраическое уравнение нечётной степени с вещественными коэффициентами имеет, по крайней мере, один вещественный корень.
Уравнения с произвольными буквенными коэффициентами степени не выше четвёртой разрешены алгебраически, т. е. для корней этих уравнений найдены общие формулы, составленные из коэффициентов уравнения посредством алгебраических действий.
В этом смысле уравнения с произвольными коэффициентами степени выше четвёртой не могут быть разрешены алгебраически (теорема Абеля); однако, если коэффициенты уравнения какой угодно степени выражены числами, всегда есть возможность вычислить с желаемой степенью приближения все его корни как вещественные, так и мнимые. Способы такого вычисления излагаются в высшей алгебре.
Методы решения целых алгебраических уравнений
Разложение на множители
Часть целых алгебраических уравнений 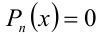
Если разложение на множители удалось выполнить, то решение алгебраического уравнения сводится к решению совокупности нескольких уравнений, но более низкой степени. Неравенство после разложения на множители можно решать методом интервалов.
Пример:
Решить уравнение
Решение:
Из 1-го уравнения находим корни 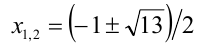
Пример:
Найти все положительные корни уравнения
Решение:
Покажем, что второе уравнение в совокупности не имеет положительных решений. Действительно, рассмотрим функцию 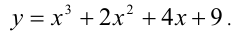
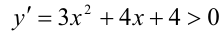
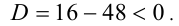
Ответ:
Подбор корня с последующим понижением степени уравнения
При решении алгебраических уравнений и неравенств степени выше второй можно использовать общий принцип последовательного понижения степени уравнения (неравенства).
Пусть требуется решить уравнение n -й степени
где 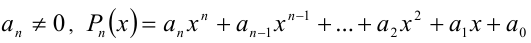
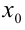

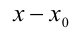
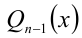
Пример:
Решить уравнение
Решение:
Заметим, что x = 2 является корнем данного уравнения. Найдём другие корни этого уравнения:
Решая уравнение 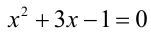
Эта ссылка возможно вам будет полезна:
Пример:
Решить уравнение
Решение:
Легко заметить, проанализировав структуру уравнения, что числа x = 0 и x = -10 являются решениями данного уравнения. С другой стороны, ясно, что это квадратное уравнение, а поэтому может иметь не более двух корней. Так как два корня уравнения уже подобраны, то других корней нет.
В некоторых случаях, для того чтобы не подбирать корень «вслепую», можно воспользоваться следующим методом.
Метод поиска рациональных корней у многочленов с целыми коэффициентами
Для решения такого рода уравнений и неравенств используется метод, в основе которого лежит Теорема 9 из предыдущего пункта. Рассмотрим подробнее суть этого метода. Пусть требуется найти рациональные корни уравнения n -й степени
причём все коэффициенты 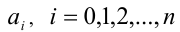

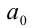
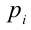
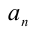
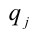
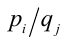
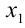
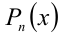
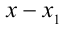

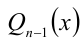
Пример:
При каких натуральных n уравнение 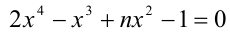
Решение:
Воспользуемся приведённым выше методом. Свободный член имеет два целочисленных делителя: ± 1, а старший коэффициент — два натуральных делителя: 1,2. Поэтому рациональные корни следует искать среди чисел 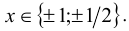
Ответ:
Метод неопределённых коэффициентов
Иногда для решения целых алгебраических уравнений (неравенств) с одной или несколькими неизвестными используют метод неопределённых коэффициентов. Пусть, например, решается уравнение
Суть метода состоит в том, что многочлен 
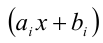
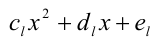
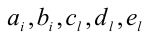
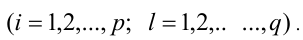
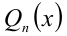
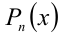
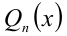
когда равны коэффициенты при одинаковых степенях переменной x, то, приравнивая эти коэффициенты, получают систему уравнений относительно неизвестных коэффициентов. Эту систему решают (или подбирают любое решение). Найденные таким способом коэффи-циенты 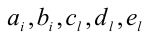
Рассмотрим применение этого метода на примере решения кубического уравнения. Допустим, требуется решить уравнение
Известно, что многочлен третьей степени всегда можно представить в виде произведения многочленов первой и второй степеней. Таким образом, сразу для всех действительных значений переменной x должно выполняться равенство
где числа а,b,c являются в данном случае искомыми неопределён-ными коэффициентами. Найдём их значения. После этого останется подставить их в правую часть (1) и, приравняв её к нулю, решить уравнение 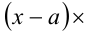
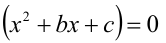
Чтобы найти коэффициенты а,b,c, раскроем скобки в правой части тождества (1) и приведём образовавшийся при этом многочлен к стандартному виду
Многочлены третьей степени тождественно равны тогда и только тогда, когда равны коэффициенты при одинаковых степенях x . Приравнивая коэффициенты при 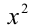
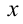
решая которую (можно даже просто подобрать любое решение этой системы) находим коэффициенты.
Пример:
Решить уравнение
Решение:
Воспользуемся для решения методом неопределённых коэффициентов. Будем искать разложение многочлена, стоящего в левой части уравнения, в виде
Раскрыв скобки, приведём многочлен в правой части к стандартному виду
Приравнивая коэффициенты слева и справа при 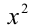
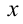
Найдя подбором решение 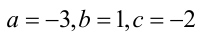
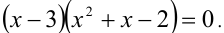
Пример:
При каких значениях а все корни уравнения 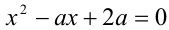
Решение:
Чтобы первое из уравнений имело корни, необходимо, чтобы его дискриминант был неотрицателен, т.е.
Далее, второй многочлен в силу теоремы Безу должен делиться нацело на первый многочлен. Иными словами, должно найтись такое b , что при всех действительных x справедливо тождество
Для нахождения неопределённых коэффициентов (в данном случае в их роли выступают а и b ) воспользуемся известным фактом, что два кубических многочлена, стоящие по разные стороны от знака равенства, тождественно равны тогда и только тогда, когда равны коэффициенты при одинаковых степенях переменной x . Приравнивая эти коэффициенты, получаем систему уравнений
Метод умножения на функцию
Иногда, применяя приём умножения обеих частей уравнения (неравенства) на некоторую функцию, удаётся упростить уравнение (неравенство).
Пример:
Решить уравнение
Решение:
Заметим, что x = — 1 (и вообще никакое отрицательное число) не является корнем данного уравнения. Домножим обе части данного уравнения на выражение (х +1). Получаем уравнение-следствие
множество решений которого состоит из всех решений исходного уравнения и числа x = -1. Это число является посторонним корнем, возникшем как раз в результате умножения уравнения на функцию, имеющую действительный нуль. Применяя известную формулу сокращенного умножения, получаем существенно более простое уравнение 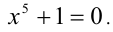
Ответ: уравнение не имеет решений.
Рассмотрим некоторые виды целых алгебраических уравнений, решаемые в основном при помощи специально подобранных подстановок.
Понятие алгебраического и трансцендентного уравнения и методов их приближенного решения
Введем понятия алгебраического и трансцендентного уравнения.
Алгебраическое уравнение — уравнение, в котором переменная 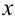
Примерами алгебраических уравнений могут служить уравнения вида: 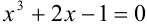
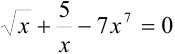
Уравнение, содержащее неизвестную переменную под знаком логарифма, тригонометрических функций, обратных тригонометрических функций или в показателе степени некоторого числа, называется трансцендентным.
Примерами трансцендентных уравнений могут служить уравнения вида:
Решить предложенное уравнение — значит найти все значения переменной 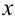
Из курса алгебры нам известны методы и приемы решения некоторых видов алгебраических и трансцендентных уравнений: например, квадратных уравнений; уравнений, решаемых методом группировки и вынесения за скобки общего множителя. Но даже решение несложного кубического уравнения вызовет у нас определенные сложности. Если нс удастся решить заданное уравнение привычными способами, существуют методы приближенного решения уравнений, состоящие из двух этапов:
1. отделение корней;
2. уточнение корней до заданной степени точности с помощью одного из следующих методов:
Этап отделения корней необходим для того, чтобы определить, какому промежутку принадлежат корни уравнения. На этом этапе обычно используется графический способ.
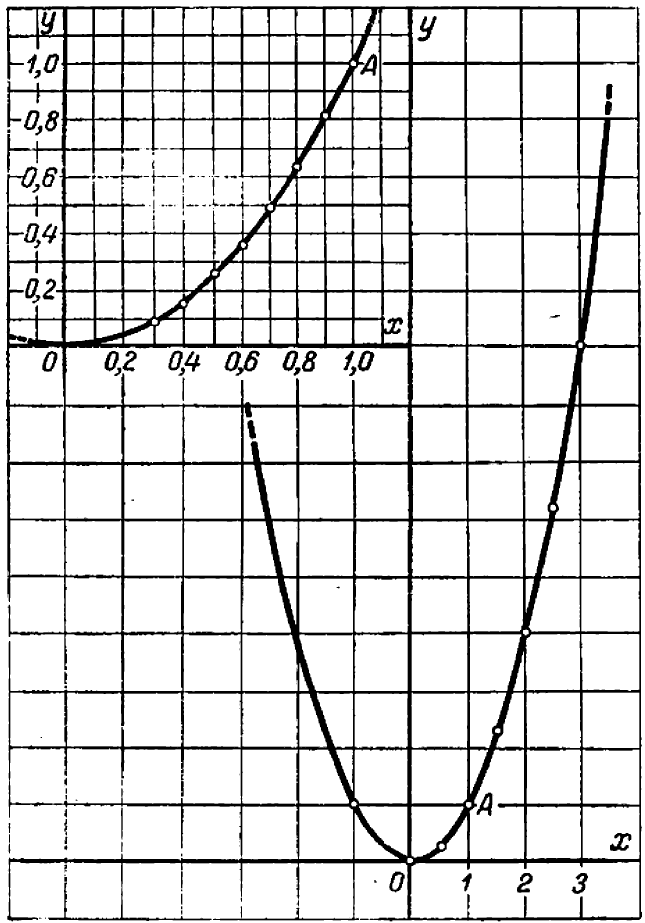
Пример:
Определить промежуток, которому принадлежат корни уравнения 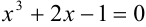
Решение:
Преобразуем данное уравнение к виду: 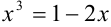
Построим графики функций 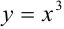
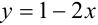
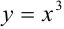
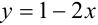
По рисунку видим, что графики функций 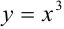
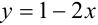
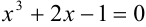
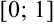
Ответ: 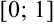
Эта лекция взята с главной страницы на которой находится курс лекций с теорией и примерами решения по всем разделам высшей математики:
Другие лекции по высшей математике, возможно вам пригодятся:
Алгебраические уравнения и их геометрическое истолкование
Уравнение с одной буквой (неизвестным)
Один из основных вопросов, которыми занимается алгебра, заключается в решении уравнений нормального вида. Так называются уравнения, у которых в левой части стоит многочлен, расположенный по степеням неизвестной буквы, а в правой части — нуль.
Степень многочлена в левой части носит название степени уравнения.
Мы встречались не раз с уравнениями, которые не имели нормального вида: таковы, например, уравнения 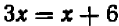
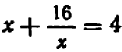
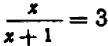
Подобного рода уравнения могут быть приведены к уравнениям нормального вида. Для этого до статочно освободиться от дробей, затем перенести на лево члены, стоящие в правой части, сделать приведение подобных членов и, наконец, правильно расположить члены.
Таким образом, привести заданное уравнение к уравнению нормального вида удается по большей части несложными приемами.
Напротив, нахождение всех корней уравнения представляет собою более трудную задачу, в особенности в том случае, если уравнение высокой степени.
Уравнение первой степени (линейное) имеет вид 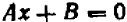
Уравнение второй степени (иначе квадратное) имеет вид 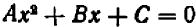
Уравнение третьей степени (иначе кубическое) имеет вид 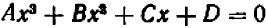
Так можно продолжать и дальше. Ради единообразия неизвестное здесь обозначено буквой 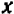
Уравнение первой степени мы решаем (см. гл. 6) следующим образом: свободный член переносим направо 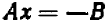
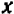
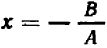
В случае уравнений второй степени или высших степеней решение уравнения тесно связано с разложением левой части на линейные множители. Так, например, уравнение 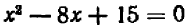
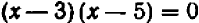
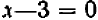
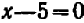
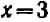
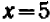
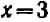
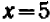
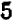
В отдельных примерах нам удавалось разлагать трехчлен второй степени на линейные множители; более полно общий прием разложения (по средствам «выделения квадрата») будет рассмотрен в главе 12.
Что касается уравнений третьей, четвертой и высших степеней, то, не говоря об отдельных частных случаях, разложить их левую часть на множители весьма трудно. С другой стороны, очень просто можно составить уравнение, имеющее наперед заданные корни; при этом степень уравнения в точности будет равняться числу корней.
Например, пусть заданы три числа: 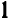
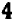
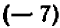
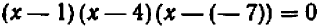
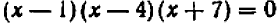
Производя умножение, получаем окончательно: 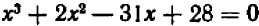
Можно доказать, что число корней уравнения никогда не превышает его степени. Но иногда оно бывает меньше степени уравнения.
Например, уравнение 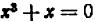

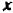
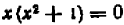
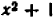
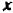
Совокупность точек на числовой оси, являющихся корнями уравнения (иначе, удовлетворяющих этому уравнению), дает нам геометрическое представление этого уравнения.
Уравнение с двумя буквами (переменными)
Нам хорошо известно, что решением (корнем) уравнения с одной неизвестной буквой называется всякое значение входящей буквы, удовлетворяющее уравнению.
Если уравнение содержит две неизвестные буквы, понятие решения должно быть обобщено и именно следующим образом: решением уравнения с двумя неизвестными буквами называется пара значений двух неизвестных, удовлетворяющая уравнению.
Так, пара чисел 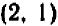
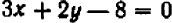

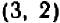
В случае уравнения с двумя неизвестными найти и перечислить все решения, как правило, невозможно. Уже простейшие примеры, вроде 
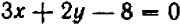
Поэтому, если в уравнение входят две (или более) неизвестных буквы, их называют обыкновенно не неизвестными, а переменными (переменными величинами).
Алгебраическое уравнение с двумя буквами считается нормальным, если в правой части стоит нуль, а в левой — многочлен, расположенный по обеим буквам.
Уравнения с двумя буквами (как и уравнения с одной буквой) классифицируются по степеням: степенью уравнения называется степень многочлена, стоящего в его левой части, причем обе буквы считаются главными.
Уравнения первой степени (линейные) имеют вид 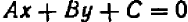
Уравнения второй степени (квадратные) имеют вид 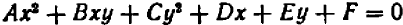
Отдать себе отчет в том, какова совокупность решений данного уравнения, нам помогает геометрическое представление уравнения: оно делает наглядной ту зависимость, которая существует между значениями букв, удовлетворяющими уравнению. Познакомимся ближе с этим геометрическим представлением.
Так как у нас имеется не одна, а две буквы, допустим, 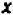
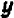
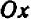
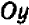
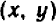
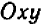
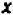
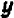
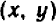
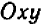
Пример:
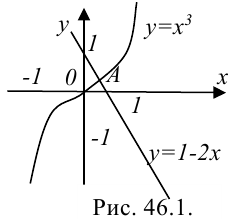
Рассмотрим уравнение 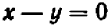
Его графиком является совокупность точек 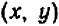
Пример:
Второй пример возьмем более сложный. Пусть нам дано уравнение второй степени: 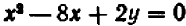
Посмотрим, как можно наметить его график.
Ничего не стоит решить уравнение относительно буквы 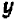
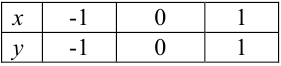
Дальше можно составить табличку числовых значений переменной 
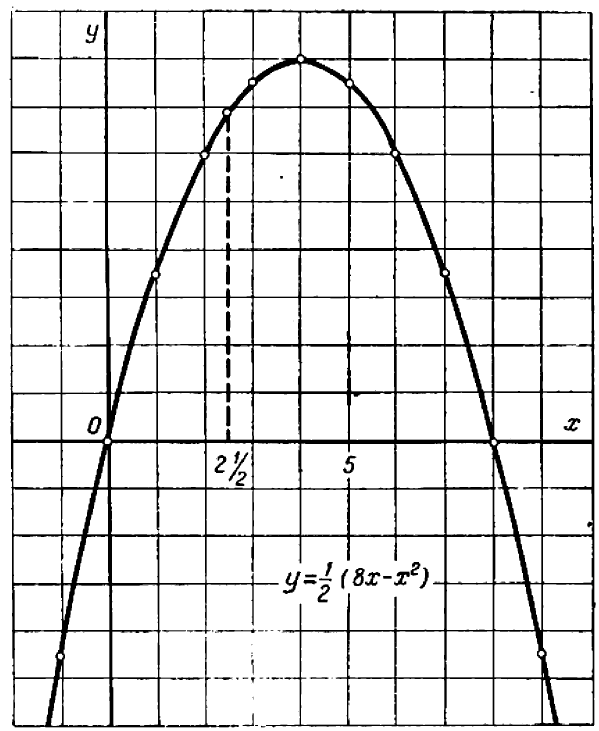
Каждую полученную точку сейчас же отмечают на черте же. Точки располагаются с известной правильностью.
Чертеж 39 показывает, что при возрастании значений 
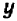
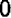
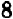
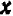
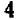
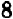
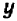
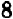
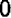
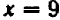
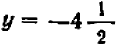
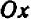
При 
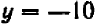
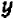
Можно букве 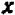
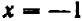
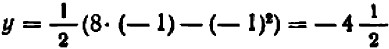
Полезло убедиться, что точки, получающиеся при подстановке дробных значений 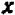
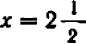
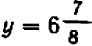
Поставим себе еще и такой вопрос: имеет ли наш график какие-нибудь точки на оси 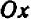
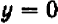

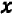

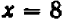
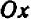
Хотя мы отметили на чертеже не свыше десятка точек, положение которых нам известно вполне точно, тем не менее правильность их расположения не оставляет сомнений в том, что все остальные, не отмеченные нами, точки графика лежат на некоторой плавной кривой, проходящей через отмеченные точки.
Эта кривая и есть график нашего уравнения. Провести ее от руки не представит труда.
Правда, полученная таким образом кривая даст возможность лишь приближенно судить о положении тех точек графика, координаты которых не были вычислены.
Использованный нами прием получения графика носит название построения графика по точкам.
Постараемся дать описание этого приема, не связывая его с каким-либо определенным примером. Пусть дано некоторое уравнение, содержащее буквы 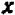
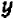
Посмотрим, существуют ли такие точки графика, которые имеют заранее назначенную абсциссу, скажем, 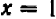
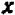

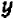
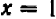
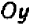

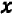
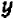
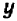
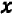
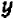
Разумеется, можно было бы также решить данное уравнение относительно буквы 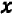
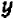
Примечание:
Иные уравнения — таковы, что не существует ни одной точки, координаты которой удовлетворяли бы уравнению.
Тогда график отсутствует или представляет собою «пустое место».
Этим свойством обладает, например, уравнение 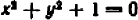
В редких случаях график может оказаться состоящим из одной точки или нескольких точек (в конечном числе). Так, уравнение 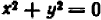

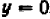
Действительно, каждый из квадратов 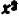
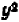
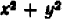
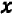
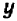
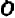
Линейное уравнение с двумя переменными
На чертеже 40 изображен график уравнения 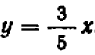
Это — прямая линия, проходящая через начало координат и расположенная в первой и третьей четвертях.
Уравнение показывает, что величина у прямо пропорциональна величине 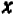
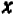
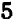
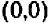
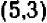
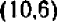
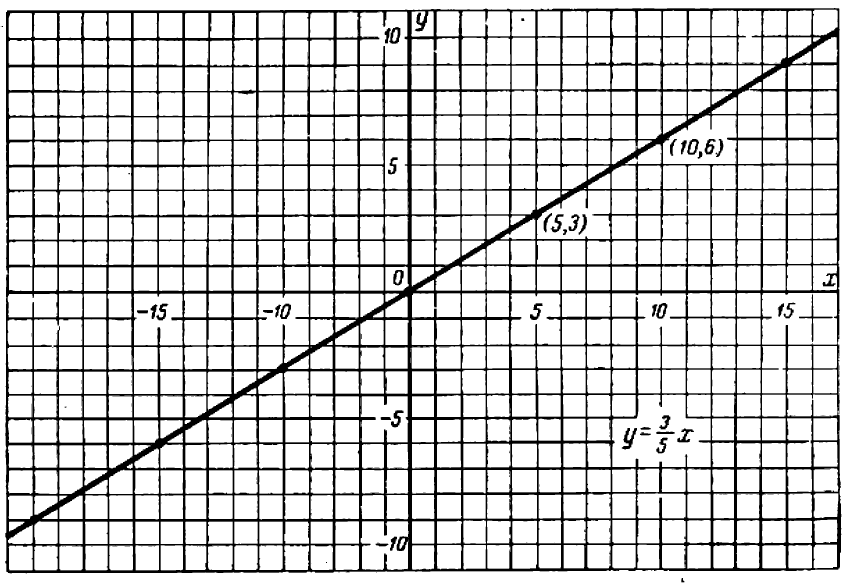
Эти точки отмечены на чертеже. Чтобы перейти от одной такой точки к следующей (считая вправо), достаточно отсчитать « 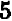
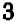
Коэффициент пропорциональности 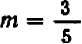
таким образом, определить направление нашей прямой.
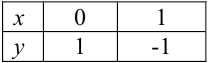
Если бы вместо уравнения (I) было задано, например, уравнение 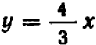
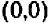
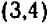
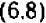
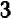
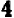
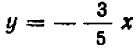
При значениях 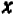
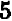
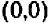
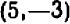
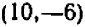
Отсчитывать нужно « 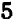
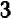
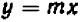

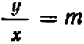
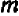
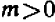

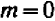
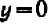

Чем меньше 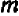
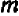
Коэффициент 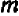
Обратим внимание на то, чем график уравнения 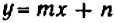
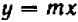
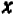
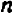


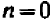
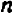
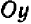

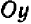
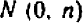
Таким образом, направление прямой 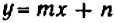
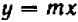
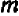
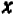
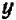
Другими словами, прямые 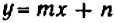
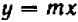
На черт. 41 изображен график уравнения 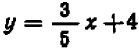
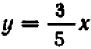
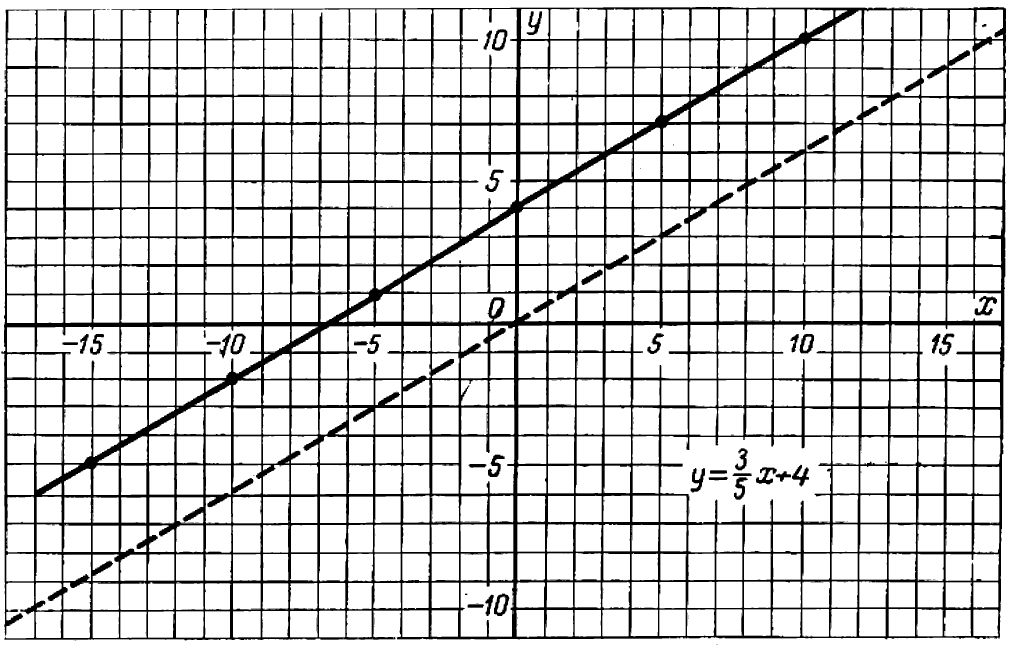
Пусть буква 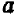

Нам нужно установить, какова совокупность точек на плоскости 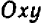
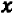
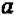
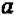
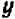
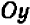
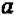
Итак, уравнение вида 
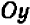
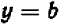

Из предыдущего следует весьма важное заключение: всякое уравнение, линейное относительно буквы 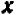
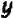
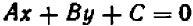
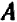
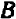
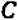
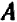
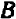
Действительно, если буква 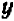
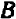
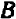
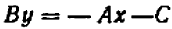
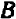
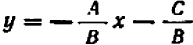
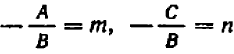
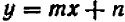
Если же буква 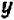

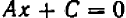
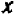


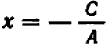

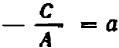
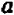
Рассматривать случай, когда 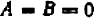
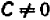
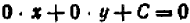
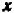
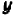
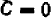
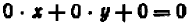
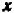
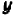
Раз известно, что линейное уравнение 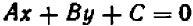
В самом деле, прямая определяется двумя точками: значит, достаточно сделать две числовые подстановки.
Проще всего установить точки пересечения прямой с осями 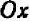

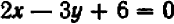
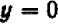
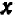
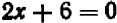

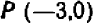

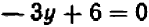
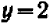
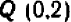
Указанный прием неудобен только в том случае, если точки 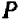
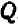

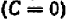
Например, чтобы построить график прямой 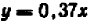



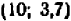
Нелинейные уравнения с двумя переменными
Мы видели, что если заданное уравнение — линейное (т. е. первой степени) относительно букв 

Дальнейшие примеры покажут, что если заданное уравнение — не линейное (т. е. степени второй или выше) относительно букв 

Степень уравнения относительно букв 

Мы рассмотрим здесь только несколько наиболее простых и важных примеров кривых, преимущественно второго порядка.
Пример:
С этим уравнением мы уже встречались. Оно говорит о том, что переменные величины 

Можно ли решить уравнение относительно 


Итак, пусть теперь 
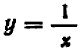
Это равенство свидетельствует, что 



Ограничиваясь пока положительными значениями величины 


Попробуем взять и дробные значения 
Получающиеся на чертеже точки имеют правильное расположение: через них можно с уверенностью про вести плавную кривую. Менее ясно пока, как вести кривую влево, в промежутке от 
и станем отмечать новые точки. Теперь становится ясно, что с убыванием положительных значений 



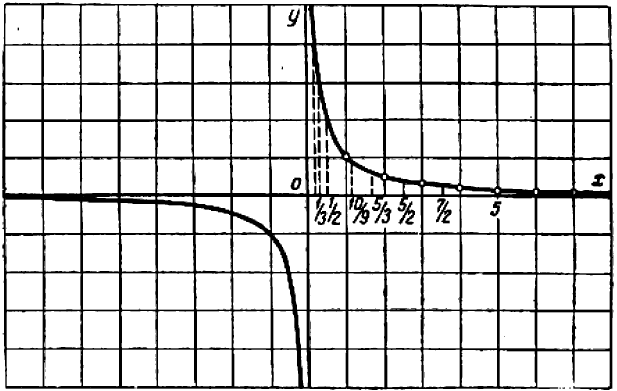
Вся полученная кривая расположена в первой четверти. Если бы мы пожелали давать букве 
Обе «ветви». рассматриваемые совместно, образуют кривую, называемую «гиперболой».
Гипербола — кривая второго порядка.
Пример:
Подставляя положительные значения 
Отметив соответствующие точки на чертеже, мы видим, что при увеличении абсциссы 


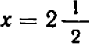
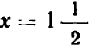
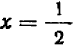
В первой клеточке 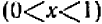
Последняя табличка позволяет заключить, что. под ходя к началу 
Обращаясь к отрицательным значениям 
Полученная кривая носит название параболы(см. черт. 43).
Парабола — кривая также второго порядка.
Пример:
При подстановке больших значений 
Напротив, при подстановке значений, близких к нулю, кубы убывают быстрее, чем квадраты:
Поэтому кривая 
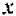
На параболу 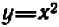

Общий вид кривой 
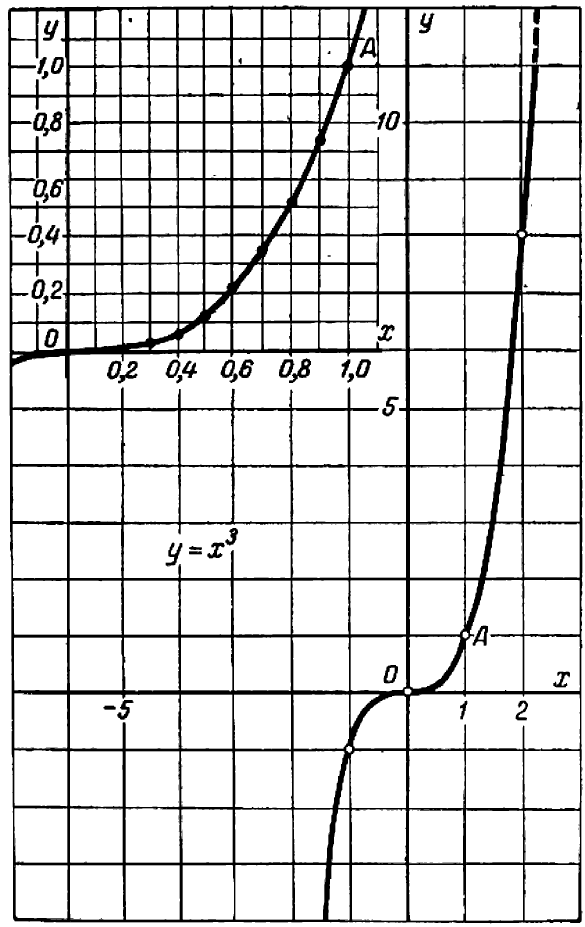
Это — кривая третьего порядка.
Алгебраические уравнения и алгоритм их решения
Общая теория уравнений
Тождества:
Введем понятие тождественного равенства функций на числовом множестве X.
Пусть функции у = f(х) и у = F(х) имеют области определения А и В соответственно, и X является подмножеством как A, так и В (но не обязательно совпадает с пересечением А и В). Тогда функции у = f(х) и у = F(х) определены на X.
Функции у=f(х) и у=F(х) называются тождественно равными на числовом множестве X, если для любого числа х из X выполняется равенство f(х)=F(х). В этом случае говорят, что равенство f(х)=F(х) является тождеством на множестве X.
Разумеется, равенство f(х)=F(х) может быть тождеством на некотором множестве X, но не быть тождеством на каком-нибудь другом множестве Y . Рассмотрим, например, функции у=х и у =|x|. На множестве X положительных чисел эти функции тождественно равны: если х — положительное число, то |х|=х. На множестве же Y всех действительных чисел эти функции не являются тождественно равными: при отрицательных значениях х равенство
не имеет места, так как при этих значениях |x|= — х.
Совершенно так же определяется понятие тождественного равенства для функций нескольких переменных. Например, функции 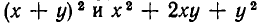
Функции же z=х+у и z =|х+у | тождественно равны лишь на множестве пар чисел х, у , для которых 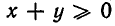
Область допустимых значений
Тождественные преобразования многочленов и алгебраических дробей изучались в начальной алгебре, и мы не будем подробно останавливаться на этом вопросе. Разберем лишь вопрос об области допустимых значений функционального равенства. Пусть дано равенство вида
Может случиться, что функции у=f(x) и у=F(x) определены не для всех значений х . Областью допустимых значений аргумента х для равенства (1) мы будем называть множество всех значений х, при которых определены и левая и правая части этого равенства.
Например, для тождества
областью допустимых значений является совокупность всех действительных чисел, из которой исключены числа 2 и 4 (при х=2 не определена функция 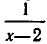
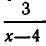
Следует иметь в виду, что такие преобразования, как приведение подобных членов, могут привести к изменению области допустимых значений. Например, тождество (2) справедливо для всех значений х , кроме х=2 и х=4. Если же мы приведем подобные члены, то получим тождество
справедливое для всех без исключения значений х.
Уравнения
Обычно когда даны две функции у=f(х) и у=F(х), то неизвестно, каково множество, на котором эти функции тождественно равны. Поэтому возникает следующая задача: найти все значения х, для которых выполняется равенство
При такой постановке задачи (*) называют уравнением с неизвестным х , а все х , при которых функции у=f(х) и у=F(х) принимают одинаковые значения, — корнями или решениями этого уравнения.
Итак, уравнение f(x) =F(х) выражает задачу об отыскании таких значений переменного х, при которых функции f(x) и F(x) имеют одинаковые значения. Решить уравнение — это значит найти все такие значения х, т. е. все корни (решения) уравнения.
Областью допустимых значений для уравнения (1) называют множество всех х у при которых определены обе функции у=f(х) и у=F(х). Например, для уравнения
область допустимых значений определяется условиями:
Область допустимых значений может заранее ограничиваться некоторыми условиями. Например, могут иметь смысл лишь положительные или лишь целые корни. В этом случае надо рассматривать уравнение лишь для положительных (или целых) значений х.
Тогда мы считаем, что функции f(x) и F(х) заданы на некотором множестве X, и рассматриваем уравнение лишь на этом множестве.
Пусть даны два уравнения
Обозначим множество корней уравнения (1) через M, а множество корней уравнения (2) через N. Если 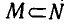
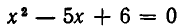
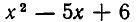
Если множества М и N корней уравнений (1) и (2) совпадают, то эти уравнения называются равносильными. Иными словами, уравнения
равносильны, если всякий корень уравнения (2) является корнем уравнения (3) и, обратно, всякий корень уравнения (3) является корнем уравнения (2).
В частности, уравнения равносильны, если множества М и N — пусты, то есть если каждое из уравнений не имеет решений.
Если уравнения (2) и (3) равносильны, то каждое из них является следствием другого.
Следует отметить, что понятие равносильности уравнений существенно зависит от того, какие значения корней считаются допустимыми. Рассмотрим, например, уравнения:
Корнями первого уравнения является число х=3, а второго — числа 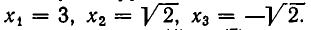
Совокупности уравнений
Пусть задано несколько уравнений
и требуется найти все значения х, которые удовлетворяют хотя бы одному из этих уравнений. Тогда говорят, что задана совокупность уравнений, а такие значения х называют решениями или корнями этой совокупности. Следует различать совокупность уравнений и систему уравнений — для системы уравнений требуется искать значения неизвестных, которые удовлетворяют всем уравнениям, а для совокупности — хотя бы одному из уравнений.
Чтобы отличать совокупность уравнений от системы уравнений, мы будем обозначать совокупность квадратными скобками, а систему — фигурными скобками.
имеет одно решение 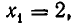
имеет три решения
Обозначим множество решений уравнения 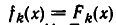
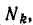
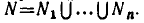
состоит из чисел 2, 3 (решений уравнения 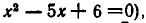
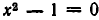
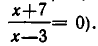
Две совокупности уравнений
называются равносильными, если они имеют одно и то же множество корней.
Например, совокупности уравнений
равносильны — их корнями являются числа 2, —2 и —3.
Преобразования уравнений
При решении уравнений мы переходим от одного уравнения к другому, пока не придем к уравнению вида х = а или совокупности уравнений такого вида. Возьмем, например, уравнение
Прибавляя к обеим частям этого уравнения (—Зх+3) и приводя подобные члены, получаем уравнение
А теперь умножим обе части уравнения (2) на и получим, что
В процессе решения этого уравнения мы прибавляли к обеим частям уравнения некоторое алгебраическое выражение (а именно, —Зх+3), умножали обе части уравнения на одно и то же число (а именно, на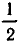
Однако не всегда одинаковые преобразования обеих частей уравнения приводят к уравнению, равносильному первоначальному. Рассмотрим уравнение:
Его решением является х = 3. Если же мы умножим обе части уравнения на х — 2, то получим уравнение:
Это уравнение, кроме решения х=3, имеет еще решение х= 2— оно имеет лишний корень по сравнению с (4).
С другой стороны, если мы возьмем уравнение (5), имеющее решения х=2, х=3, и «сократим» его на х — 2 (то есть разделим обе части уравнения на х — 2), то получим уравнение 2х+1= =х+4 с единственным решением х=3. Значит, здесь мы в процессе решения потеряли корень х=2.
Не является «безобидным» и прибавление к обеим частям уравнения одного и того же алгебраического выражения. Например, уравнение
имеет решение х =2. Но если прибавить к обеим частям этого уравнения выражение 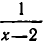
для которого х =2 не является решением — обе части этого уравнения не имеют смысла при х=2. Таким образом, произошла потеря решения.
Эти примеры наглядно показывают, что при преобразовании уравнений необходима осторожносгь — неправильно преобразуя уравнение, мы можем как приобрести лишние решения, так и потерять решения данного уравнения. При этом надо иметь в виду, что приобретение лишних решений не столь опасно, как потеря существующих. Ведь после того, как уравнение решено, можно подставить все найденные решения в заданное уравнение и отобрать те из решений, которые ему удовлетворяют. А потерянные решения восстановить уже нельзя.
Из изложенного видно, что, прежде чем решать конкретные виды уравнений, надо познакомиться с общей теорией уравнений, выяснить, какие преобразования приводят к равносильным уравнениям, какие дают посторонние решения, а при каких решения могут быть потеряны. Только после этого мы сможем решать уравнения «с открытыми глазами».
Теоремы о равносильности уравнений
Сформулируем сначала условия, при которых одно уравнение является следствием другого уравнения. Потом из этих условий будут получены условия равносильности уравнений.
Теорема:
Если к обеим частям уравнения
прибавить функцию 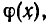
являющееся следствием данного.
Доказательство:
В самом деле, пусть а—корень уравнения (1). Тогда f(а)=F(а). Но 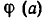
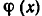
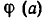
которое показывает, что число а является корнем уравнения (2). Таким образом, всякий корень уравнения (1) является корнем уравнения (2), то есть уравнение (2) является следствием уравнения (1).
Условие, что функция 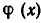
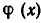
Прибавление к обеим частям уравнения одного и того же выражения не может привести к приобретению посторонних корней, если это прибавление не сопровождается приведением подобных членов или иными преобразованиями, меняющими область определения уравнения (например, сокращением дробей). Рассмотрим, например, уравнение
Если прибавить к обеим частям — 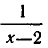
Перейдем к вопросу об умножении обеих частей уравнения на одно и то же выражение.
Теорема:
Если обе части уравнения
умножить на функцию 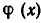
являющееся следствием уравнения (3).
Доказательство.
Пусть а — корень уравнения (3). Тогда справедливо равенство f(а)=F(а). Умножим обе части этого равенства на число 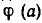
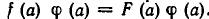
Из доказанных теорем следует, например, что уравнение
является следствием уравнения
Действительно, уравнение (5) получается из уравнения (6) прибавлением к обеим частям функции Зх+2 и умножением полученного уравнения на х + 2.
Многочлены определены при всех значениях х. Поэтому прибавление к обеим частям уравнения многочлена, равно как и умножение обеих частей
уравнения на многочлен, приводит к уравнению, являющемуся следствием исходного.
Оговорка о том, что 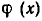
и умножим обе части этого уравнения на 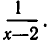
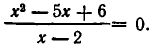
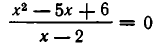
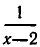
Докажем теперь теоремы о равносильности уравнений. Чтобы доказать равносильность двух уравнений, надо показать, что пер вое из них является следствием второго, а второе — следствием первого.
Теорема:
Если функция 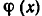
Доказательство:
Мы уже видели, что при условии теоремы уравнение (9) является следствием уравнения (8). Но уравнение (8) в свою очередь получается из уравнения (9) прибавлением к обеим частям функции — 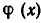
Так как функция 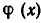
Из доказанной теоремы вытекает правило перенесения слагаемых из одной части уравнения в другую: если некоторое слагаемое данного уравнения перенести из одной части в другую, изменив знак этого слагаемого на противоположный, то получится уравнение, равносильное данному.
В самом деле, в силу теоремы 3 уравнения
равносильны: уравнение (11) получается путем прибавления функции — 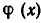
Кратко правило перенесения слагаемых формулируют так: всякое слагаемое можно перенести из одной части уравнения в другую, изменив при этом его знак на противоположный.
Из доказанной теоремы вытекает, что всякое уравнение f(х) =F(х) можно заменить равносильным ему уравнением вида Ф(х) = 0. Для этого достаточно перенести F(х) в левую часть уравнения, заменив знак на противоположный, и положить f(х)— F(х) =Ф (х).
Теорема:
Если функция 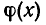
Доказательство:
Мы уже видели (теорема 2), что уравнение (13) является следствием уравнения (12). Докажем, что уравнение (12) в свою очередь является следствием уравнения (13). Уравнение (12) получается из уравнения (13) умножением обеих частей на функцию 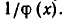
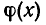
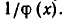
Из доказанной теоремы вытекает, например, что уравнения
равносильны в области действительных чисел. В самом деле, уравнение (15) получается из уравнения (14) умножением на функцию 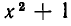
не являются равносильными — второе получается из первого умножением на функцию 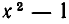
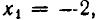
Уравнения (12) и (13) могут быть неравносильными и в том случае, когда множитель 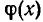
неравносильны: множитель 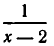
Если в ходе решения уравнения приходилось умножать обе части этого уравнения на выражение 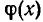
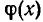
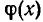
В первом случае среди найденных корней могут оказаться посторонние корни, и надо проверить все найденные корни, удовлетворяют ли они первоначально заданному уравнению. Во втором же случае возможна потеря корней, и мы должны подставить в заданное уравнение значения неизвестного, при которых теряет смысл 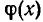
Из теоремы 4 непосредственно вытекает справедливость утверждения: если обе части уравнения умножить на произвольное отличное от нуля число, то получим уравнение, равносильное данному.
Это утверждение кратко формулируют так: обе части уравнения можно умножать на произвольное отличное от нуля число.
Уравнения с одним неизвестным
Алгебраические уравнения с одним неизвестным:
Рациональным алгебраическим уравнением с одним неизвестным называют уравнение вида
где R(х) — алгебраическая дробь относительно х. К такому виду можно в силу теорем 3 и 5, привести любое уравнение 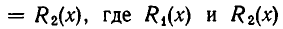
является рациональным алгебраическим. В дальнейшем мы будем называть такие уравнения просто алгебраическими.
Применяя теоремы о равносильности уравнений, можно заменить каждое уравнение вида (1) равносильным ему уравнением вида:
где f(x)— многочлен от х. Для этого надо записать дробь R(x) в виде отношения двух многочленов. Мы получим уравнение:
где f(х) и 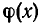
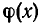
Пример:
Перенесем 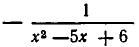
Приравнивая нулю числитель этой дроби, получаем уравнение х—2=0, корнем которого является число х=2. Однако при x=2 дробь 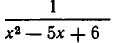
Метод разложения на множители
Рассмотрим некоторые методы решения алгебраических уравнений, а также отдельные виды таких уравнений.
Выше было сказано, что при решении уравнения его заменяют другими уравнениями или совокупностями уравнений, равносильными заданному, но более простыми
Рассмотрим следующий пример. Пусть надо решить уравнение:
Мы знаем, что произведение может равняться нулю тогда и только тогда, когда хоть один из его сомножителей равен нулю. Поэтому, чтобы решить уравнение (1), надо найти все значения, при кототых хоть один из сомножителей равен нулю. А это все равно, что решить совокупность уравнений
Решая ее, находим для х значения 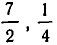
Метод, примененный для решения уравнения (1), в общем виде формулируется так.
Теорема:
Если функции 
равносильно совокупности уравнений
Доказательство:
Пусть а — одно из решений совокупности (3). Это означает, что а является корнем одного из уравнений этой совокупности, например, уравнения 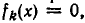
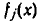
так как один из сомножителей 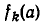
Наоборот, пусть а — корень уравнения (2). Тогда f (а)=0, то есть 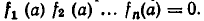

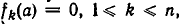
Пример:
Левая часть этого уравнения разлагается на множители следующим образом:
Отсюда следует, что уравнение (4) равносильно совокупности уравнений:
Решая уравнения этой совокупности, получаем корни уравнения (4):
не равносильны, так как при х = 0 функция 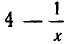
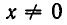
В некоторых случаях разложение на множители связано с искусственными преобразованиями. Рассмотрим, например, уравнение:
Нетрудно заметить, что
Поэтому уравнение (б) можно записать в виде:
Таким образом, все свелось к решению совокупности двух квадратных уравнений:
Решая их, находим корни уравнения (6):
Метод введения нового неизвестного
Наряду с методом разложения на множители часто применяется другой метод — введение нового неизвестного.
Рассмотрим следующий пример:
Если раскрыть скобки, то получится уравнение четвертой степени, решить которое довольно сложно. Мы поступим иначе. Обозначим 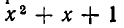
Поэтому уравнение (1) после введения нового неизвестного z принимает вид
Решая это квадратное уравнение, получаем, что его корни равны:
Но 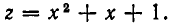
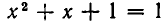
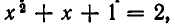
Решая ее, получаем:
Метод, примененный для решения уравнения (1), в общем виде заключается в следующем.
Пусть дано уравнение F(х)=0 и пусть функцию F(х) можно представить в виде 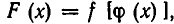
Введем новое неизвестное z, положив 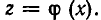
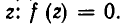
Теорема:
Если а — один из корней уравнения f(z) = 0, а b — один из корней уравнения 
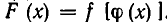
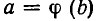
Доказательство. Пусть b — корень уравнения 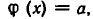
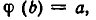
Таким образом, b удовлетворяет уравнению F (х) = 0.
Обратно, пусть b — корень уравнения F(х)=0 и 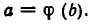
Следовательно, а — корень уравнения f(z)=0. Теорема доказана.
Из доказанной теоремы следует, что решение уравнения вида 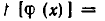
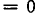

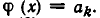
Биквадратные уравнения
Метод замены неизвестного при меняется для решения уравнений вида
Такие уравнения называют биквадратными. Чтобы решить уравнение (1), положим 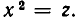
Его корнями являются числа:
Поэтому корни уравнения (1) получаются путем решения уравнений 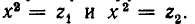
Четыре корня возникают при различных комбинациях знаков:
При решении биквадратных уравнений (как и при решении квадратных уравнений) иногда приходится извлекать квадратные корни из отрицательных чисел. Это приводит к так называемым комплексным числам, которые будут изучены в главе V.
Пример. Решить уравнение
Полагая 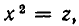
Его корнями являются числа 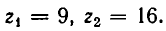
Возвратные уравнения 3-й и 4-й степеней
Многочлен n-й степени
называется возвратным, если его коэффициенты, одинаково уда ленные от начала и от конца, равны между собой. Иными словами, коэффициенты возвратного многочлена n-й степени удовлетворяют условию
Алгебраическое уравнение вида f(х)=0, где f(х) — возвратный многочлен, называют возвратным уравнением. Примерами таких уравнений являются:
Рассмотрим решение возвратных уравнений третьей и четвертой степеней. Возвратное уравнение третьей степени имеет вид:
Группируя члены, разложим выражение в левой части уравнения на множители:
Отсюда видно, что одним из корней уравнения (1) является х=—1 . Два других корня получаются путем решения квадратного уравнения
Пример:
Разлагая левую часть уравнения на множители, получаем:
Корни квадратного уравнения 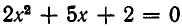
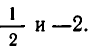
Приведем пример задачи, сводящейся к разобранному типу уравнений.
Задача:
Из квадратного листа жести со стороной а см вырезают по углам четыре квадратика со стороной х см и делают из получившейся фигуры коробку. При каком значении х объем коробки равен 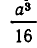
Решение:
Основанием коробки является квадрат со стороной а-2x, а ее высота равна х. Значит, объем коробки равен 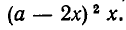
Положим 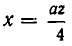
Разлагая на множители, получаем
Поэтому корни нашего уравнения равны
Из условия задачи следует, что 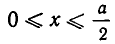
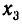
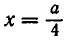
Теперь рассмотрим возвратное уравнение 4-й степени:
Так как 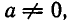
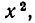
Введем новое неизвестное z, положив 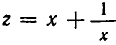
Следовательно, уравнение (3) превращается в квадратное уравнение относительно z
Решив это уравнение, найдем его корни 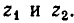
Она сводится к совокупности квадратных уравнений:
Пример. Решить уравнение
Перепишем это уравнение в виде
и введем новое неизвестное 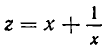
Решая его, находим: 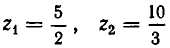
Из них получаем:
Наряду с уравнениями вида (1) и (2) рассматривают так называемые кососимметричные уравнения, или, иначе, возвратные уравнения второго рода. При n=4 они имеют вид:
Это уравнение сводится к
После этого вводят новое неизвестное по формуле 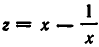
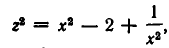
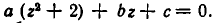
Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:




















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
http://uztest.ru/abstracts/?id=24&t=2
http://lfirmal.com/ponyatie-algebraicheskogo-i-transtsendentnogo-uravneniya-i-metodov-ih-priblizhennogo-resheniya/