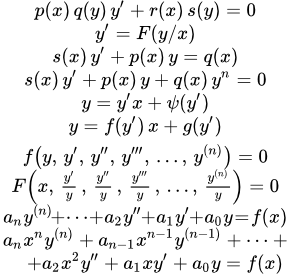К какому типу относится уравнение онлайн

Калькулятор Обыкновенных Дифференциальных Уравнений (ОДУ) и Систем (СОДУ)

Порядок производной указывается штрихами — y»’ или числом после одного штриха — y’5

Ввод распознает различные синонимы функций, как asin , arsin , arcsin

Знак умножения и скобки расставляются дополнительно — запись 2sinx сходна 2*sin(x)

Список математических функций и констант :

• ln(x) — натуральный логарифм

• sh(x) — гиперболический синус

• ch(x) — гиперболический косинус

• th(x) — гиперболический тангенс

• cth(x) — гиперболический котангенс

• sch(x) — гиперболический секанс

• csch(x) — гиперболический косеканс

• arsh(x) — обратный гиперболический синус

• arch(x) — обратный гиперболический косинус

• arth(x) — обратный гиперболический тангенс

• arcth(x) — обратный гиперболический котангенс

• arsch(x) — обратный гиперболический секанс

• arcsch(x) — обратный гиперболический косеканс

Дифференциальные уравнения по-шагам

Результат

Примеры дифференциальных уравнений

• Простейшие дифференциальные ур-ния 1-порядка
• Дифференциальные ур-ния с разделяющимися переменными
• Линейные неоднородные дифференциальные ур-ния 1-го порядка
• Линейные однородные дифференциальные ур-ния 2-го порядка
• Уравнения в полных дифференциалах
• Решение дифференциального уравнения заменой
• Смена y(x) на x в уравнении
• Другие

Указанные выше примеры содержат также:

• квадратные корни sqrt(x),
  кубические корни cbrt(x)
• тригонометрические функции:
  синус sin(x), косинус cos(x), тангенс tan(x), котангенс ctan(x)
• показательные функции и экспоненты exp(x)
• обратные тригонометрические функции:
  арксинус asin(x), арккосинус acos(x), арктангенс atan(x), арккотангенс actan(x)
• натуральные логарифмы ln(x),
  десятичные логарифмы log(x)
• гиперболические функции:
  гиперболический синус sh(x), гиперболический косинус ch(x), гиперболический тангенс и котангенс tanh(x), ctanh(x)
• обратные гиперболические функции:
  asinh(x), acosh(x), atanh(x), actanh(x)
• число Пи pi
• комплексное число i

Правила ввода

Можно делать следующие операции

2*x — умножение 3/x — деление x^3 — возведение в степень x + 7 — сложение x — 6 — вычитание Действительные числа вводить в виде 7.5, не 7,5

Чтобы увидеть подробное решение,
помогите рассказать об этом сайте:

Типы дифференциальных уравнений

Далее в тексте – функции своих аргументов. Штрих ′ означает производную по аргументу. – постоянные.

Дифференциальные уравнения первого порядка

Особенности дифференциальных уравнений первого порядка

При решении уравнений первого порядка функцию y и переменную x следует считать равноправными. То есть решение может быть в виде так и в виде .

Дифференциальные уравнения первого порядка, разрешенные относительно производной

Уравнения с разделяющимися переменными

;
. Подробнее
Приводящиеся к уравнениям с разделяющимися переменными:
Подробнее

Однородные уравнения

Однородные уравнения не меняют свой вид при замене
,
где t – постоянная. При такой замене производная не меняется:
.
В общем виде обобщенно однородные уравнения можно записать посредством однородных функций:
,
где и – однородные функции с равными показателями однородности, то есть обладающие следующим свойством:
.
Общий вид однородных уравнений также можно выразить через произвольную функцию:
. Подробнее

Приводящиеся к однородным
,
где и – однородные функции с равными показателями однородности. В общем виде такие уравнения можно выразить через произвольную функцию:
. Подробнее

Обобщенно однородные уравнения не меняют свой вид при замене
,
где t – постоянная, . Для производной такая замена выглядит так:
.
В общем виде обобщенно однородные уравнения можно записать посредством однородных функций:
,
где и – однородные функции с равными показателями однородности.
Обобщенно однородные уравнения также можно записать через произвольную функцию:
. Подробнее

Линейные дифференциальные уравнения и приводящиеся к ним

• Линейное по y:
• Линейное по f(y):
• Линейное по x:
• Линейное по f(x):

Уравнения Риккати

Уравнения Якоби

Уравнения в полных дифференциалах

Интегрирующий множитель

Если дифференциальное уравнение первого порядка не приводится ни к одному из перечисленных типов, то следует попытаться найти интегрирующий множитель, чтобы свести его к уравнению в полных дифференциалах:
;
. Подробнее

Уравнения, не разрешенные относительно производной y′

Уравнения, допускающие решение относительно производной y′

Сначала нужно попытаться разрешить уравнение относительно производной y′ . Если это возможно, то уравнение может быть приведено к одному из перечисленных выше типов.

Уравнения, не разрешенные относительно производной y′

Уравнения, допускающие разложение на множители:
.
Подробнее
Уравнения, не содержащие x и y:
. Подробнее
Уравнения, не содержащие x или y:
, или . Подробнее

Уравнения, разрешенные относительно зависимой переменной y

Уравнения Клеро:
. Подробнее
Уравнения Лагранжа:
. Подробнее
Уравнения, приводящиеся к уравнению Бернулли:
;
. Подробнее

Дифференциальные уравнения высших порядков

Дифференциальные уравнения высших порядков, решаемые в квадратурах

Уравнения, содержащие переменную и старшую производную

Общий случай:
. Подробнее
Разрешенные относительно старшей производной:
. Подробнее
Разрешенные относительно переменной:
. Подробнее

Уравнения, содержащие только производные порядков n и n-1

Общий случай:
. Подробнее
Разрешенные относительно младшей производной:
. Подробнее
Разрешенные относительно старшей производной:
. Подробнее

Уравнения, содержащие только производные порядков n и n-2

Общий случай:
. Подробнее
Разрешенные относительно старшей производной:
. Подробнее

Дифференциальные уравнения, допускающие понижение порядка

Уравнения, не содержащие зависимую переменную y (и возможно несколько первых производных):
, или
. Подробнее
Уравнения, не содержащие независимую переменную x:
. Подробнее
Уравнения, однородные относительно функции и ее производных y, y′, y′′, . :
, причем
. Подробнее
Обобщенно однородные уравнения относительно переменных x, y:
, причем
. Подробнее
Дифференциальные уравнения с полной производной:
. Подробнее

Линейные дифференциальные уравнения с постоянными коэффициентами и приводящиеся к ним

Линейные однородные уравнения с постоянными коэффициентами:
. Подробнее
Линейные неоднородные уравнения с постоянными коэффициентами:
.
Решение методом Бернулли (двух функций)
Решение методом Лагранжа (вариация постоянных)
Решение линейной подстановкой
Линейные неоднородные уравнения со специальной неоднородной частью:
,
где – многочлены степеней и . Подробнее
Уравнения Эйлера:
. Подробнее

Использованная литература:
В.В. Степанов, Курс дифференциальных уравнений, «ЛКИ», 2015.
Н.М. Гюнтер, Р.О. Кузьмин, Сборник задач по высшей математике, «Лань», 2003.

Автор: Олег Одинцов . Опубликовано: 12-05-2012 Изменено: 26-11-2021